基于Levy-GARCH模型的股票市場尾部風險度量研究

朱福敏 宋佳音 劉儀榕

一、引言

金融作為實體經濟的供血系統，在支持實體經濟發展的同時也存在向實體經濟傳播風險的隱患。牢牢守住不發生系統性風險底線的一項重要工作就是防范化解金融風險、防止發生系統性金融風險。中國股市經過近三十年的發展取得顯著成效，但是相較于國外發達的股票市場依然不成熟，股指收益率序列存在頻繁的波動率集聚和跳躍震蕩現象，相應的股崩與暴跌風險也更高(陳國進和張貽軍，2009[1]；劉圣堯等，2016[2])，導致系統性金融風險也隨之劇烈波動。如2018年3月，美國總統特朗普簽署總統備忘錄，對600億中國商品加征關稅，引發全球資本市場動蕩，2018年3月22日至2018年6月22日，僅三個月的時間，滬深股市市值蒸發超過70萬億。新冠病毒感染疫情也給金融市場造成了巨大沖擊，2020年2月3日當天，上證綜合指數下跌7.7%，超過3 000只股票跌停。

尾部風險的準確測度不僅有助于評估系統性風險，而且可以用于風險管理、風險傳染等更深層次的研究。在尾部風險測度中，對金融市場的波動集聚、杠桿效應和尖峰厚尾等現象的刻畫發揮了重要作用，而隨機跳躍行為和尾部極端事件在資產定價和風險測度上也十分重要(劉圣堯等，2016[2]；郭文旌等，2013[3])，但是目前的風險測度研究往往只注重厚尾特征(Kim等，2011[4]；吳鑫育等，2014[5]；王耀東等，2021[6])。為同時捕捉杠桿效應和跳躍行為、優化尾部風險測度，本文引入Levy-GARCH模型描述收益率動態。Levy-GARCH模型極具包容性，巧妙地結合了Levy過程與GARCH模型，可以選擇性地呈現非對稱性、非高斯性等特征，部分模型還具有仿射結構。在此基礎上，依托國內金融市場，構建20種描述不同跳躍行為和異方差效應的Levy-GARCH模型，考察跳躍形態和杠桿效應在收益率擬合及尾部風險測度上的表現，包括在險價值(Value at risk，VaR)和條件在險價值(Conditional Value at risk，CVaR)的度量差異，并結合回溯測試檢驗Levy-GARCH模型在尾部風險價值度量上的綜合表現，分析不同特征對尾部風險測度的影響，研究結論有助于揭示我國股票市場系統性風險特征，可進一步用于金融風險管理和風險傳染機制研究。

通過Levy-GARCH模型將非對稱性和跳躍形態引入尾部風險測度研究，可以發現條件方差模型的仿射結構并非必需，杠桿效應是提升尾部風險測度效果的重要因素之一；不同于資產定價研究中無限活動率跳躍過程的優越表現，在我國股市的尾部風險測度上反而是有限活動率跳躍過程表現更優，特別是在股災期間，有限跳躍模型的綜合表現優于無限活動率跳躍模型。綜合來看，具有非對稱性、非高斯性和非仿射結構的Levy-GARCH模型的尾部風險測度表現更好，且有限活動率跳躍過程的綜合表現優于無限活動率跳躍過程。

二、文獻綜述

尾部極端金融事件雖發生概率低，可一旦發生就會對投資者情緒和金融市場的穩定產生重大且持續的影響，因此尾部風險管理成為學術界和監管者的研究重點，而風險管理的有效性在很大程度上由風險度量的準確性所決定。早期，在險價值(Value at Risk，VaR)被廣泛應用于金融市場尾部風險的測度，該模型的計算基于收益率序列服從正態分布的假設，然而，大量實證研究表明金融資產的收益率序列普遍存在“尖峰厚尾”現象，基于正態分布計算的VaR會低估實際風險(劉慶富等，2006[7]；吳鑫育等，2013[8]；邸浩等，2018[9])。由于資產收益率及其波動率是VaR測度的關鍵變量(吳鑫育等，2021[10])，因此，學者們一方面改進收益率的分布假定，如假設收益率服從偏t分布、混合正態分布等(黃友珀等，2015[11]；王良等，2017[12]；吳鑫育和周海林，2018[13])，另一方面改進擬合收益率的模型和方法，如在模型中考慮資產價格運動的波動率集聚現象、杠桿效應以及非高斯的跳躍特征等(Kim等，2011[4]；王耀東等，2021[6])。

在尾部風險測度研究中，存在多種尾部風險測度指標。VaR這一測度指標可以更直觀地反映資產價格風險，也被業界廣泛使用。雖然VaR具有簡單易操作的特點，但是表示一定置信水平下VaR值平均水平的條件在險價值(Conditional VaR，CVaR)在測度極端風險時更接近實際損失(楊子暉等，2019[14])，且條件在險價值是滿足二階隨機占優的一致風險測度，適用于分散投資和資產收益率大幅波動時的風險測量(Kim等，2010[15]；Kim等，2011[4])。在現有的尾部風險研究中，眾多學者更關注風險的傳染或聯動現象，會采用基于VaR構建的其他風險測度指標。如用于研究個股對市場極端風險敏感性的尾部β(Van Oordt和Zhou，2016[16]；姜富偉等，2022[17])、方便研究風險傳染機制的條件在險價值(CoVaR，conditional VaR(1)雖然CoVaR和CVaR的全稱一致，但二者描述的概念并不相同。CVaR用于描述損失超過VaR閾值時的預期損失，體現單一資產的風險，和AVaR(Average Value at Risk)及條件期望損失(expected shortfall，ES)等價(Kim等，2010[15]；邸浩等，2018[9])；而CoVaR用于描述當一個主體相應的損失達到閾值時另一個主體的VaR，體現不同資產間風險的影響(Tobias和Brunnermeier，2016[18])。)(Tobias和Brunnermeier，2016[18]；張偉平等，2021[19])，還有邊際損失預期(Marginal Expected Shortfall，MES)(Acharya等，2017[20])、SRISK(Brownlees和Engle，2017[21])等風險測度指標。風險測度指標的構建與選擇主要取決于研究對象，尾部風險的準確測度則是依賴于對收益率分布的準確描述。

現有研究中，主要有三種方式描述收益率分布，包括經驗分布法、分位數回歸法和條件方差法。經驗分布法是從歷史樣本中提取符合條件的損失作為相應的VaR，多用于尾部β的計算(Van Oordt和Zhou，2016[16]；姜富偉等，2022[17])。分位數回歸法在風險傳染研究中使用較為廣泛，選取可能影響風險的宏觀狀態變量進行分位數回歸，根據回歸結果計算風險測度指標(Tobias和Brunnermeier，2016[18]；劉曉東和歐陽紅兵，2019[22]；林娟和趙海龍，2020[23])。條件方差法主要是依賴于波動率模型來描述資產價格規律，再通過收益率分布計算相應的VaR和其他風險測度(Kim等，2011[4]；吳鑫育等，2014[5]；王耀東等，2021[6])。在上述三種方法中，基于資產價格動態規律的條件方差法準確度相對較高(2)分別使用經驗分布法(Van Oordt和Zhou，2016[16])和分位數回歸法(Tobias和Brunnermeier，2016[18]；林娟和趙海龍，2020[23])計算VaR值并進行回溯測試，并將其與Levy-GARCH模型做對比，發現經驗分布法表現較差，分位數回歸法的表現優于正態分布假設的各類GARCH模型和各個HNGARCH模型，但是綜合表現不如帶跳躍的GARCH、GJR-GARCH和NGARCH模型，這同時也反映了跳躍形態對于尾部風險測度的重要性。。

為了捕捉資產收益率的波動集聚性及時變性，進而改善尾部風險的測度效果，國內外學者主要采用GARCH模型或SV模型對資產收益率過程進行建模(Kim等，2011[4]；吳鑫育等，2013[8]；吳鑫育等，2014[5]；黃友珀等，2015[11]；吳鑫育等，2018[13]；邸浩等，2018[9]；吳鑫育等，2021[10]；王耀東等，2021[6])。針對資產有偏和厚尾的特征，吳鑫育等(2014)[5]引入雙杠桿門限SV模型來測度金融市場的動態風險價值VaR，研究表明考慮了波動集聚和杠桿效應的模型具有更優越的極端風險測度能力。Kim等(2011)[4]則針對美國歷史上4次重大股崩分別建立了厚尾分布下的ARMA-GARCH模型，并用在險價值測度VaR和CVaR對股指分布的尾部風險進行了度量和檢驗。王耀東等(2021)[6]綜合考慮了資產價格的杠桿效應、尖峰厚尾和尾部非對稱性等特征，引入Skew-t分布，建立GJR-GARCH-Skew-t模型，在此基礎上研究尾部風險傳染路徑。研究表明，厚尾的GARCH模型能夠較為準確地度量極端事件發生的概率。

上述模型雖然可以反映資產收益率的尖峰厚尾特征與波動率的集聚特征，但是并未全面考慮資產價格跳躍行為對風險度量的影響。為描述跳躍行為，有學者在波動率模型中引入跳躍成分。早期研究主要關注資產價格中的少量大幅跳躍并建立有限跳躍模型(Merton，1976[24]；Kou，2002[25])，然而，一些實證研究表明，有限跳躍模型不足以刻畫金融市場中大量存在的高頻小跳現象，因此，后續學者引入Levy過程解決上述問題(Carr和Wu，2004[26]；Ornthanalai，2014[27])，并在不同方向進行完善和擴展。如Bates(2012)[28]建立了Levy過程驅動下的單因子和雙因子隨機波動率模型，以考察股崩背景下標準普爾500指數收益率的波動跳躍情況。Christoffersen等(2012)[29]基于有限跳躍過程建立時變跳躍強度的離散時間模型，得到了跳躍風險在總方差風險中占比較高以及跳躍存在集聚現象的證據。Ornthanalai(2014)[27]基于Levy過程建立跳-擴散雙因子期權定價模型，通過對標準普爾500指數的研究發現，資產定價模型中更應該考慮無限活動率跳躍過程而非擴散波動過程。中國股市也存在顯著的波動率集聚、跳躍群聚和非對稱的杠桿效應(郭文旌等，2013[3]；任光宇和呂小鋒，2021[30])，熊市中利空消息帶來的不確定性致使投資者要求獲得更高的期望收益率，這種杠桿效應是導致暴跌的重要因素之一(龔銳等，2005[31])。吳恒煜等(2014)[32]結合帶跳躍的隨機過程、條件異方差效應和杠桿效應提出了非高斯Levy-GARCH模型，研究顯示該模型能夠很好地捕捉金融數據跳躍特征、集聚現象和杠桿效應三個特點。在美國市場的股指期權定價研究、大陸和香港市場的權證定價研究中，無窮活動率跳躍過程在提升定價精度上表現優于有限跳躍過程和連續擴散過程(吳恒煜等，2014[32]；吳恒煜等，2014[33]；Zhu等，2020[34])。

上述研究顯示，已有眾多研究關注波動率模型驅動的尾部風險度量，但是全面考慮波動率非對稱回饋效應和跳躍形態的尾部風險度量研究較少。為綜合對比非對稱性和非連續性對尾部風險的影響，本文在Levy-GARCH框架下，全面對比杠桿效應和跳躍形態在收益率擬合與在險價值評估等方面的表現，考察尾部風險的經典測度VaR和滿足一致可加性條件的CVaR在不同收益率分布假設下的風險評估情況，并用基于例外值和尾部分布密度檢測的回溯測試對在險值的測度效果進行評價。

與現有文獻相比，本文全面系統地研究了異方差性、非對稱性和非高斯性對風險度量的影響。選擇4種不同GARCH模型和包括標準布朗運動在內的5個Levy隨機過程來構建Levy-GARCH模型，模型覆蓋率是其他文獻所未達到的。其次，根據Levy-GARCH的條件特征函數推導出基于傅里葉變換(fast fourier transform，FFT)的極大似然函數及尾部風險測度表達式，封閉的數值解為實證研究提供了極大的便利。此外，實證研究發現，無論是收益率擬合、預測還是尾部風險的測度，正態分布假設都不能反映收益率分布的尖峰厚尾特征，跳躍過程下的Levy-GARCH模型在收益率擬合與風險測度上都表現出更優良的效果；在我國股市的尾部風險測度上，和資產定價領域研究發現不同的是，有限跳躍過程的綜合表現優于無窮活動率跳躍過程，這一發現對于我國股市風險特征的研究具有潛在價值。

接下來主要內容安排如下：第三部分將介紹描述杠桿效應和跳躍行為的Levy-GARCH模型，并介紹Levy-GARCH模型在險價值的計算表達式；第四部分為實證研究，將展示基于傅里葉變換的極大似然估計、擬合檢驗和回溯測試，以及上證綜合指數的風險價值，并引入基于例外值檢測的CLR似然比檢驗和基于分布函數的BLR似然比檢驗，對各個模型進行綜合比較，評價模型對在險價值度量的影響，同時對其他市場指數做穩健性檢驗；第五部分為結論。

三、Levy-GARCH模型

(一)GARCH族模型

以往文獻通常采用GARCH模型來描述收益率序列中的條件異方差特征。傳統GARCH模型一般假設股指的對數收益率yt滿足如下形式：

yt=ct+εt

(1)

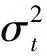
然而，上述GARCH模型中條件波動率σt是zt-1的對稱函數，導致波動率的大小僅取決于歷史殘差的大小，而與其方向無關，這與金融市場中資產收益率和波動率之間存在負向相關關系，即杠桿效應的實際情況不相符(龔銳等，2005[31])。為了測度所選股指數據是否有杠桿效應，選取三類常見且具有代表性的帶杠桿效應的GARCH模型，分別為GJR-GARCH模型(Glosten等，1993[35])、NGARCH模型(Engle和Ng，1991[36])以及HN-GARCH模型(Heston和Nandi，2000[37])。表1為各個帶杠桿效應GARCH模型的具體表達形式及模型相應屬性。

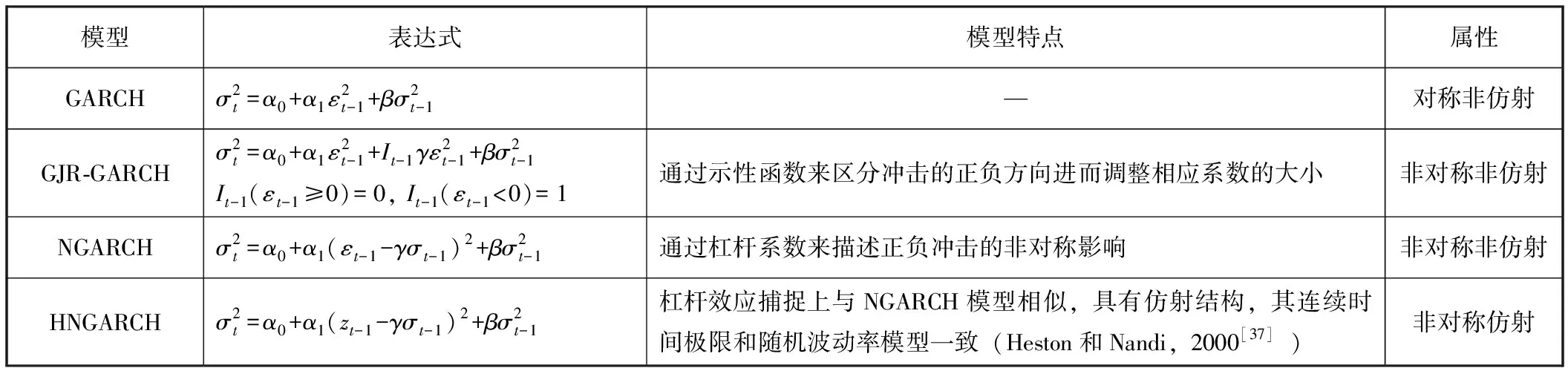
表1 帶杠桿效應的GARCH波動率模型的表達式

(二)Levy過程

證券資產收益率的隨機過程除了具備時變波動率和杠桿效應以外，還具有非連續性的跳躍(吳恒煜等，2014[32]；吳恒煜等，2014[33]；Zhu等，2020[34])，可由Levy過程刻畫(3)關于Levy過程的具體定義以及更多詳細內容請參見吳恒煜等(2014)[32]、吳恒煜等(2014)[33]的研究。。相當一部分Levy過程沒有確切的密度函數解析式，但是其特征函數可以根據Laplace分解得到。對特征函數φ(u)=E(eiux)=e-ψX(u)，相應特征指數ΨXt(u)可表達為Levy-Khinchine公式：

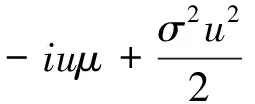
(2)

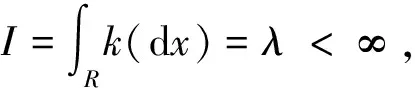
在式(1)的基礎上，引入Levy過程來刻畫資產價格的跳躍行為，建立Levy-GARCH模型，可寫成如下形式(參考Zhu等，2020[34])：

yt=μt+xtΔXt-φΔXt(xt)

(3)

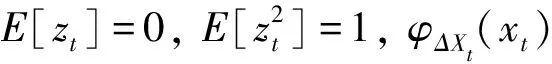
采用五種Levy過程，其中四種為跳躍形態。用于描述擴散波動的維納過程也是Levy過程的一種，因其用于Black-Scholes模型而將其稱為BS過程；跳躍過程中包括有限活動率的莫頓跳躍擴散過程(Merton Jump，MJ)，無限活動率的方差-伽馬過程(Variance Gamma，VG)、正態逆高斯過程(Normal Inverse Gaussian，NIG)和經典調和穩態過程(Classical Tempered Stable，CTS)，這四類跳躍過程在收益率模型中較為常見(Carr和Wu，2004[26]；Ornthanalai，2014[27])，相應的Levy測度、矩母指數及屬性如表2所示，配合表1中具有不同屬性的GARCH模型，可以構建20種Levy-GARCH模型，所建立模型的屬性由Levy過程和GARCH模型共同決定。

表2 跳躍過程的Levy測度、矩母指數

(三)尾部風險測度VaR和CVaR

根據Kim等(2011)[4]，結合Levy-GARCH模型，可以得到顯著性水平η下的動態形式VaR和CVaR：

VaRt+1,η(yt+1)=xt+1·VaRt+1,η(ΔXt+1)+φΔXt+1(xt+1)-μt+1

CVaRt+1,η(yt+1)=xt+1·CVaRt+1,η(ΔXt+1)+φΔXt+1(xt+1)-μt+1

(4)

這里ΔXt+1=zt，其中：

(5)

特征函數與CVaRη(X)之間的關系可以表示為(參見Kim等(2010)[15]的做法)：

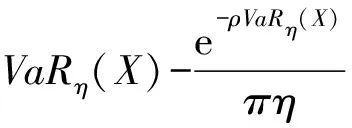
(6)

其中，ρ>0，使得u∈R時，|φX(-u+iρ)|<∞，即特征函數在實數范圍內有界。

四、實證分析

為反映我國股市二十年頻繁震蕩和幾次股災的波動跳躍情況，選取上證綜合指數(Shanghai Stock Exchange Composite Index，下述實證用簡寫SHA表示)進行實證分析，收益率數據來源于國泰安數據庫。上證綜合指數由國內交易最活躍的證券交易所上海證券交易所編制而成，是國內最早編制的股票指數，極具代表性。在實證研究中，選取上證綜合指數2002年1月7日至2019年12月31日的4 366個交易日的收益率為樣本數據，建立跳躍形態下的Levy-GARCH模型，并比較各個模型對收益率分布的擬合情況和尾部風險的度量情況，考察各個Levy形態驅動的波動率模型對國內股指收益率尾部形態的刻畫能力和風險度量能力。

(一)參數估計

由于大部分Levy-GARCH模型都沒有封閉形式密度函數，采用基于傅里葉變換的極大似然估計方法對參數進行估計，根據吳恒煜等(2014)[32]的做法，Levy-GARCH模型的殘差可以表示為εt=xtΔXt，其中，xt表示Levy過程的狀態變量，ΔXt為隨機增量。基于條件特征函數的傅里葉變換有：

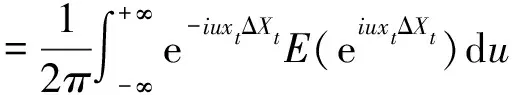
(7)

對數聯合似然函數lnL可表示為：

(8)

其中，Θ為待估參數，p(ΔXt)由傅里葉變換計算所得(4)更為詳細的關于Levy-GARCH模型基于傅里葉變換的極大似然估計方法參見吳恒煜等(2014)[33]、Carr和Wu(2004)[26]的研究。。所得參數估計結果如表3所示。其中后三列數據為Levy過程的估計參數和標準差，MJ過程的參數為{λJ，σJ，μJ}，CTS過程的特征三項為{α，λ+，λ-}等。從表3來看，各個模型的杠桿系數γ都是非常顯著的。同時風險的市場價格λ為正，即跳躍風險對收益率的影響有正的補償作用。

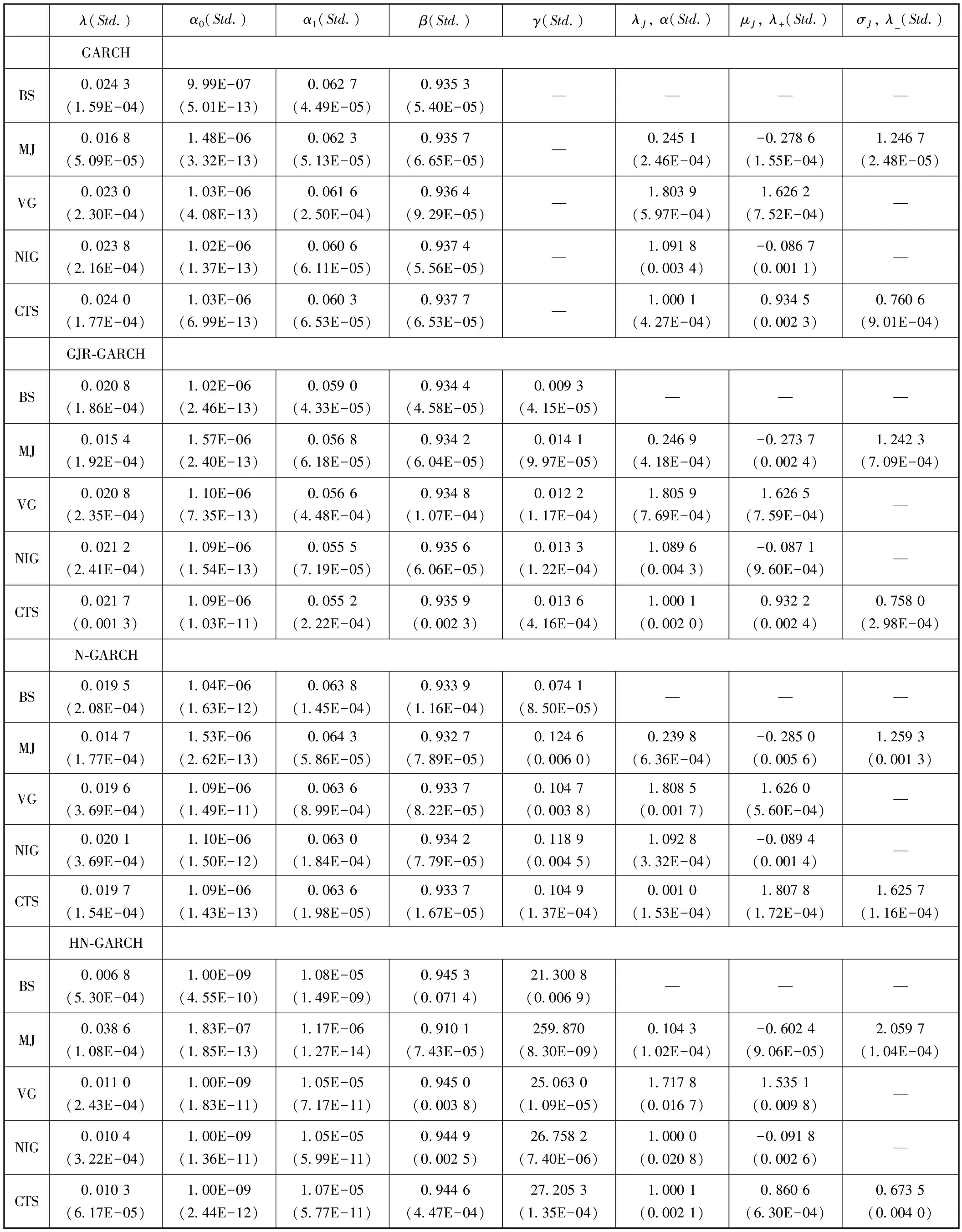
表3 參數估計結果

表4是各個模型擬合優度的相關統計評價，具體如下：

1.根據模型擬合所得殘差統計性質、KS檢驗的p值以及AIC、BIC等信息準則來看，四類GARCH模型中，非對稱非仿射的GARCH模型表現出較穩定的優越性。而在定價領域應用廣泛的仿射HN-GARCH模型擬合效果排在最后，甚至弱于傳統的對稱結構的GARCH模型，仿射結構并不能靈活地捕獲市場波動形態。

2.根據模型新息因子的KS檢驗結果，除了MJ-HNGARCH模型之外，MJ、VG、NIG和CTS過程下的GARCH族模型P值全都顯著大于0.05，而正態分布下的條件波動率模型全不顯著，顯然新息服從正態分布的假設無法被接受。

擬合結果顯示，股指收益率存在杠桿效應，但是僅刻畫杠桿效應無法捕獲非高斯特征，正態分布不能表現股指收益率的特征，各類跳躍過程在收益率序列擬合上表現更優。

(二)尾部風險度量

基于上述參數估計結果，計算各個模型的尾部風險度量VaR和CVaR值。同一跳躍波動率模型下，CVaR的估計值比VaR的值要大，特別是在波動比較頻繁和集聚或者股災背景下，VaR的估計值有明顯低估風險的趨向，而CVaR的估計值更能描述風險的損失。圖1以MJ跳躍過程下NGARCH波動率模型為例，描繪了尾部風險VaR和CVaR值以及二者之間的差別，其他所有波動率模型也存在類似的結果，此處省略。表5則列出了不同波動率模型下各個跳躍測度與正態分布假設所得在險值差異的均值和標準差。

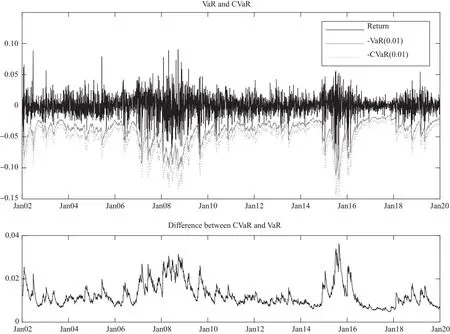
圖1 MJ跳擴散過程下NGARCH波動率模型尾部風險度量及差異比較

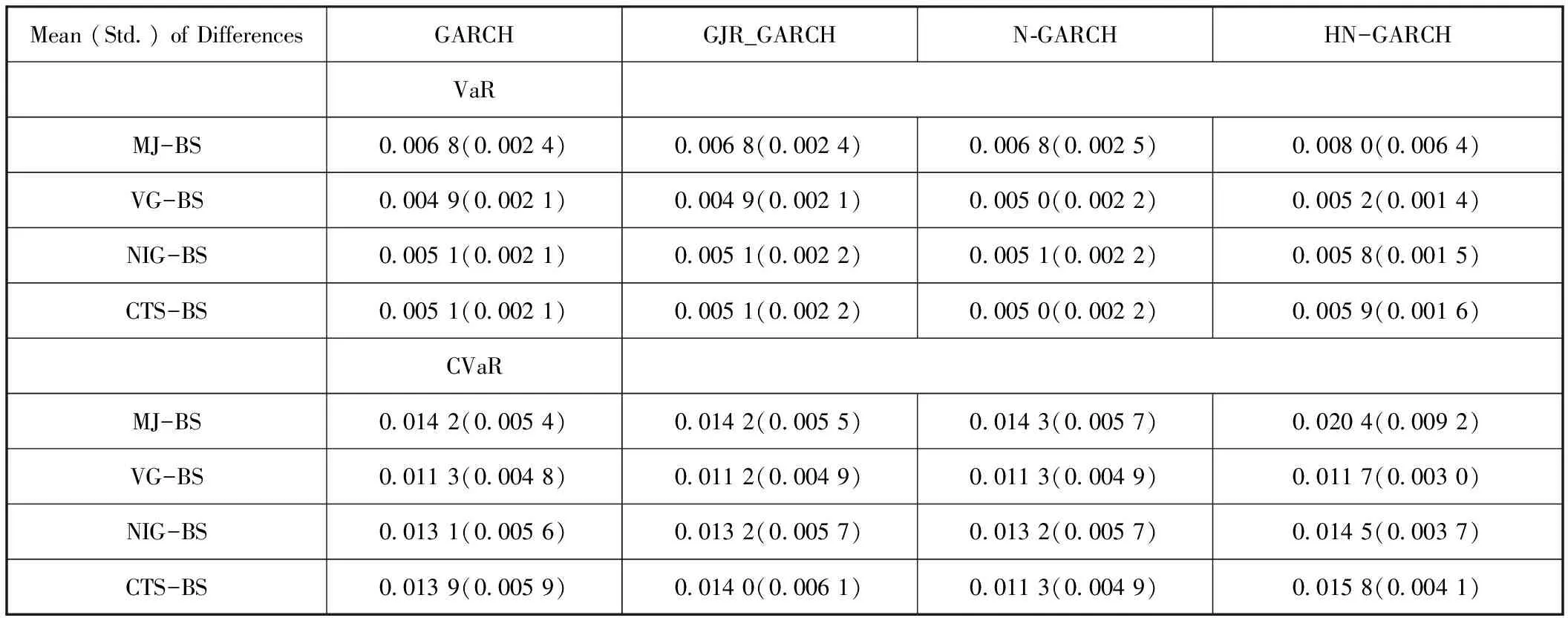
表5 不同純跳躍測度下在險值與正態分布假設所得在險值差異比較

由圖1，同一跳躍波動率模型所得CVaR值總是大于VaR值，在股價震蕩幅度頻繁且劇烈的時候，二者之間的差異更是明顯。這表明VaR值會低估風險，在出現股市異象的時候更是如此。

不同跳躍驅動下的同一波動率模型所得在險值也有區別。根據表5，正態假設下所得VaR和CVaR絕對值最小，MJ跳躍形態所得VaR值和CVaR值最大；VG、NIG和CTS跳躍波動率模型所得VaR值和CVaR值在相似水平；在非仿射GARCH模型中，各個不同跳躍形態與正態分布下的在險值之差基本一致，但是HNGARCH模型中的在險值之差相對較大。在不同Levy過程驅動下，帶杠桿效應GARCH模型和對稱的GARCH模型所得在險值之差相對較小。綜合來看，跳躍形態對風險價值的影響比杠桿效應的影響更大(5)由于篇幅限制，不同Levy測度下，捕捉杠桿效應GARCH模型與GARCH模型所得在險值差異的均值和方差未列出，以備索的方式提供。，這和參數估計的情況是一致的。

(三)回溯測試

為了對帶跳躍的波動率模型所得在險值進行準確度評判和檢驗，選用Christoffersen(1998)[38]似然比(CLR)和Berkowitz(2001)[39]似然比(BLR)進行回溯測試。

CLR是基于例外值的檢驗，是對一定置信水平下給定樣本中VaR值被超越次數的檢驗，包括三方面的檢驗：一是無條件覆蓋率，最初由Kupiec(1995)[40]提出，也稱Kupiec檢驗、違約率檢驗或者失敗比檢驗(用CLRuc表示)；二是獨立性的覆蓋率檢驗或者稱為Markov檢驗(用CLRind表示)，檢驗樣本期間例外值的相互獨立性(Christoffersen，1998[38])；三是條件覆蓋率檢驗(用CLRcc表示)，無條件覆蓋率檢驗和獨立性檢驗二者合并產生條件覆蓋率檢驗(Christoffersen，1998[38])。

條件覆蓋率檢驗可以檢驗VaR模型的有效性，通過檢驗是建立一個合適VaR模型的充分條件。然而CLR這種基于奇異值或者例外值的回溯測試方法考慮了整個收益率分布中的某個百分點或者某個置信區間，BLR檢驗則是在收益率整體密度函數基礎之上建立的回溯測試方法。BLR檢驗包括兩個方面：一是對整個收益率分布函數預測能力的似然比檢驗，即獨立性檢驗(用BLRind表示)；二是對分布函數尾部描述大額損失的預測能力檢驗(用BLRtail表示)(Berkowitz，2001[39])。

用CLR和BLR檢驗方式評估各個跳躍波動率模型下在險值計算的準確度，如表6所示，有如下情況。

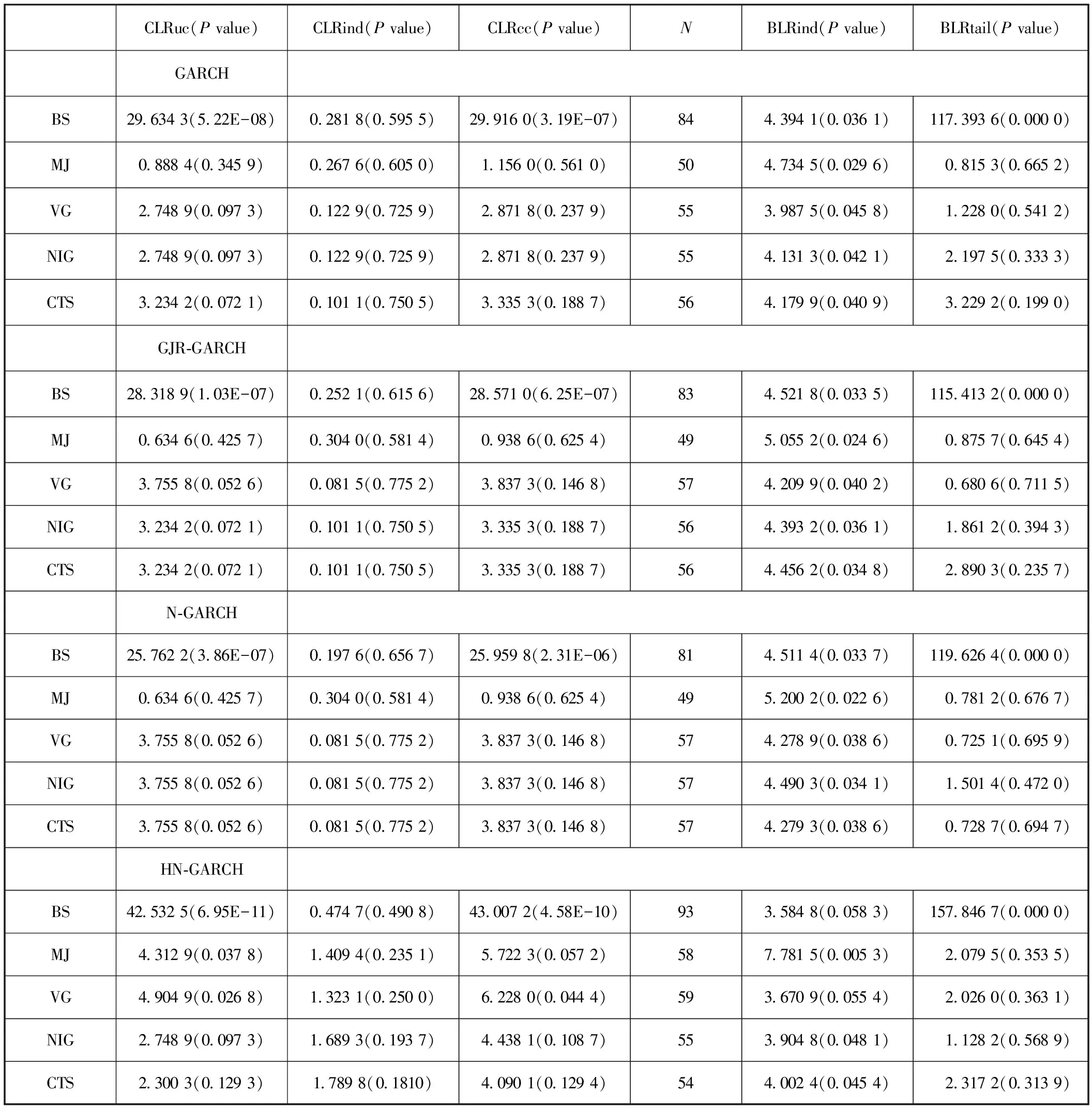
表6 SHA對數收益率在不同跳躍波動率模型下所得在險值的回溯測試結果

1.在0.05的顯著性水平上，CLR的無條件覆蓋率檢驗拒絕了正態信息假設下的所有GARCH模型，包括正態分布的非對稱GARCH，也拒絕了VG-HNGARCH模型，除此之外MJ、VG、NIG和CTS過程下GARCH、NGARCH和GJR-GARCH模型都表現良好，說明跳躍行為在尾部風險度量方面起著至關重要的作用，仿射結構的GARCH模型則與非仿射的GARCH模型存在較大差異。

2.在0.05的顯著性水平上，VaR的CLR獨立性檢驗對所有Levy-GARCH模型全部通過，說明Levy-GARCH這一條件異方差模型較好地捕獲了波動率的動態性；條件覆蓋率檢驗表明，在MJ、VG、NIG和CTS的驅動下，GARCH、NGARCH和GJR-GARCH波動率模型都取得良好的結果，對HNGARCH模型而言，VG跳躍下波動率模型表現較差，說明仿射GARCH模型不能精確捕獲波動率的動態性。

3.N代表CLR的誤判個數，即損失超過VaR預測值的個數。同一波動率模型下正態假設所得VaR的誤判率N/T最大，NIG、CTS和VG形態下所得VaR的誤判率水平相似，有限跳躍形態MJ的誤判水平最低。MJ形態下波動率模型所得VaR值最大，CLR測試結果也顯示MJ的誤判率最小，其次是NIG、CTS和VG。所有模型中GARCH、GJR-GARCH、NGARCH模型的誤判率相差不大，HNGARCH模型表現較差。

4.除了MJ跳躍形態下HNGARCH模型被BLR的獨立性檢驗拒絕外，其他跳躍波動率模型都在0.01的顯著性水平上通過BLR的獨立性檢驗，這說明仿射結構的HN-GARCH模型比其他非對稱的GARCH差，非仿射模型表現更優。

5.除正態分布假設的GARCH模型外，其他波動率模型均在0.05的顯著性水平上通過BLR的尾部檢驗，但是各跳躍過程驅動的波動率過程難以比較優劣。

以上實證結果由上證指數18年歷史數據檢驗所得，為進一步考察各個跳躍波動率模型對尾部風險的測度能力，選用2002年1月7日至2019年12月31日數據分別進行9年期、3年期短期回溯測試，以檢驗各個跳躍波動率模型的在險價值估計效果。(6)由于篇幅限制，9年期與3年期短期回溯測試結果未列出，以備索的方式提供。

9年期檢驗。2002年至2010年區間段，除HNGARCH模型，其他均可在0.05的顯著性水平上通過回溯測試。而2011年至2019年這段時間多數模型無法通過檢驗，僅部分有限跳躍模型能通過檢驗，2011—2019年間經歷了2015—2016年的股災、2018年中美貿易戰，說明這些事件對股市造成了巨大的沖擊，在股價崩盤的情況下，正態分布假設和無限活動率跳躍驅動的波動率模型不能很好地擬合收益率分布，中國股市在這個區間段以有限大跳躍為主。

3年期檢驗。在5%的顯著性水平上，2008年至2010年、2011年至2013年、2014年至2016年、2017年至2019年這幾個區間段，正態分布假設下的波動率模型無法通過檢驗，而2014年至2016年區間段，MJ過程驅動的波動率模型在誤判率、CLR回溯檢驗和BLR尾部檢驗上表現更優，說明在股災期間，有限跳躍形態可以更準確地刻畫中國市場收益率分布的厚尾特征。

在股市表征出劇烈的波動率集聚和異象跳躍的情形下，對同一波動率模型來說，正態分布假設完全不能滿足收益率擬合和風險測度的要求，無窮跳躍形態下的Levy-GARCH模型可以較穩定地滿足參數估計和風險測量的要求，而有限跳躍形態下的Levy-GARCH模型雖然表現不是十分完美，但是相比較起來能夠更好地表現股崩異象下的收益率分布，并滿足風險測度的要求。

(四)穩健性檢驗

本文同時還選擇了其他市場指數進行穩健性檢驗，包括上證A股指數(SH_A)、深證成分指數(SZC)和滬深300指數(CSI300)，這三個指數具有市場代表性，樣本區間和上證綜指的樣本區間一致。因篇幅限制，此處只展示NGARCH模型新息因子的KS檢驗和在險值回溯測試結果。

在這三個分別代表滬市、深市和滬深兩市的指數上，跳躍形態的表現呈現了與上證綜合指數相似的情況。首先在收益率擬合上，跳躍過程都在0.05的顯著性水平上通過檢驗，正態分布假設都無法通過檢驗。在回溯測試上，上證A股指數、深證成分指數和滬深300指數在無條件覆蓋率檢驗、獨立性檢驗和有條件覆蓋率檢驗上結果也較為相似，基本上是有限跳躍優于無限跳躍，跳躍過程優于正態分布假設；而在BLR檢驗中，三個指數的回溯測試結果存在一定差異，主要表現為部分無限活動率跳躍過程優于有限跳躍過程，跳躍過程優于正態分布假設。

整體上，跳躍形態的表現都優于正態分布假設，跳躍過程在上證A股指數、深證成分指數和滬深300指數上的表現基本與上證綜合指數一致，有限跳躍過程的綜合表現更優。

五、結論

股價崩盤現象表現為股市收益率急劇下跌，出現異常的波動率集聚和劇烈震蕩現象，導致收益率分布的尖峰、厚尾以及左偏更為明顯，正態分布假設下無論是參數估計還是風險測度都無法滿足金融監管需求。為了準確描述收益率的尖峰厚尾、尾部非對稱性和跳躍行為等特征，本文引入頗具包容性和靈活性的Levy-GARCH模型，選擇具有代表性的4種條件方差模型和5種Levy過程，構建了20種Levy-GARCH模型來刻畫跳躍形態和杠桿效應，針對國內上證綜指收益率的擬合、預測和風險度量得出如下結論：

第一，無論是收益率擬合、預測還是尾部風險的測度，正態分布假設都不能滿足收益率分布的尖峰厚尾要求。捕捉跳躍行為的Levy-GARCH模型對中國市場收益率數據的擬合效果較好，其中捕捉有限活動率跳躍的Levy-GARCH模型綜合表現優于帶無限活動率跳躍過程的模型，在風險測度上有更為優良的效果，而且在股災期間對中國市場收益率數據的擬合效果較好。

第二，對GARCH模型的實證分析表明，股市中確實存在收益率和波動率之間的杠桿效應，且非仿射結構的帶杠桿效應GARCH模型表現更優。首先，雖然正態分布假設下GARCH模型不能很好地描述收益率分布的特征，但是經過跳躍測度修正后的波動率模型可以通過KS檢驗，在風險測度上也表現優良。其次，不同跳躍形態下的GARCH、GJR-GARCH、NGARCH模型擬合效果相差較小，表明非對稱的跳躍過程刻畫一部分非對稱性或收益率中的杠桿效應，這在一定程度上，可弱化波動率的非對稱性。最后，非仿射的GARCH模型表現比仿射HNGARCH模型更優，HNGARCH在收益率擬合與尾部風險測度上綜合表現較差。

第三，股價表現出較為頻繁劇烈波動的時候，VaR會明顯低估尾部風險，CVaR則能更有效地度量劇烈波動下的尾部風險。有限活動率跳躍形態和無限活動率跳躍形態下同一波動率模型所得VaR和CVaR值也有差異，而無窮活動率跳躍形態下的VaR值和CVaR值水平相近。結合參數估計的顯著性和回溯測試結果，有限活動率的MJ過程所得在險價值表現最好，且擁有較好的風險評估效果，特別是在股災期間。同時，回溯測試表明描繪非對稱回饋效應的NGARCH和GJR-GARCH比HNGARCH表現更為優良。

為準確描述尖峰厚尾、杠桿效應和跳躍行為等特征，本文引入Levy-GARCH模型進行尾部風險測度研究，可以更精準地描述市場收益率的尾部風險。實證研究發現，在中國股市尾部風險測度上，同時滿足非對稱、非高斯(有限跳躍)、非仿射性質的Levy-GARCH模型表現更優。這也說明在我國股市，股指價格的下跌會導致更大的市場波動，而且股市存在頻繁的跳躍行為，因此在評估尾部風險時，應充分考慮厚尾特征、尾部非對稱性和非連續性，以免低估實際風險；在防范化解尾部風險時，應警惕下行的跳躍風險，合理應對隨之而來的市場波動甚至震蕩。