中小跨徑波紋鋼箱型橋梁力學性能研究

摘要：文章采用剛度等效方法建立了埋置式波紋鋼結構的有限元模型，通過截面應變和應力換算方法，得到了波紋鋼截面的應變、軸力和彎矩等數據，從而對波紋鋼箱型橋梁的力學性能進行了深入研究。分析可知：橋梁在荷載尤其是在車輛活載作用下受到的軸力和彎矩較大，對橋梁的結構安全性和穩定性具有重要影響；拱頂位移是衡量橋梁變形程度的重要指標之一；在荷載作用下，橋梁截面承受的應變和內力較大，需要進行合理的材料選取和結構設計以保證橋梁的安全和穩定性。

關鍵詞：中小跨徑；波紋鋼箱型橋梁；力學性能

中文分類號：U448.21+3A521714

0引言

波紋鋼橋梁作為一種重要的埋置式結構，獨特的結構形式賦予了其優異的力學性能，使其在多種工程應用中展現出顯著的優勢。然而，波紋鋼橋梁的實際應用與研究面臨著高昂的試驗成本和復雜的試驗條件，這些因素大大限制了其在工程實踐中的深入研究與廣泛應用［1］。此外，試驗研究中現場環境的不確定性也可能對試驗結果的準確性產生負面影響。針對這些挑戰，數值分析方法成為研究波紋鋼橋梁的一種有效途徑，其能夠克服現場試驗的局限性，為橋梁設計與評估提供更加準確的理論支持［2］。本文通過采用剛度等效方法建立了埋置式波紋鋼結構的有限元模型，并應用截面應變和應力換算方法，深入分析了波紋鋼箱型橋梁的力學性能，包括其應變、軸力和彎矩等關鍵參數。這一研究不僅豐富了波紋鋼橋梁的理論研究，也為實際工程應用提供了有價值的參考。

1工程概況

為了深入研究波紋鋼箱型橋梁結構的力學性能，本文選擇了位于某市繞城環線上的一座單跨波紋鋼箱型橋梁進行了有限元數值模擬。該繞城環線是該市的一項重要道路工程，全長為83.568 km，于2019年竣工。該道路按照二級公路標準建設，不同路段根據地形條件設計了不同的行車速度，設計路基寬度分別為14 m、18 m和24 m。整條線路共有648座大中型橋梁和16座小橋涵洞，橋梁和涵洞的設計荷載符合公路-Ⅰ級標準。本文選取的波紋鋼箱型橋梁位于起止樁號為K4+657.980～K4+686.980的區段，總長為29 m，路基寬度為24 m，為雙向四車道。在行車道兩側分別設置了3.5 m寬的土路肩。設計時考慮了洪水位，其中設計洪水位為2 249.680。

2建立數值模型

2.1建立幾何模型

使用ANSYS三維建模軟件創建研究對象的幾何模型，并使用網格劃分和單元屬性賦予，生成有限元模型。在具體應用中，對于波紋鋼箱型橋梁，可以忽略一些次要結構，如錐形護坡、混凝土護欄和基礎混凝土墊層，而將重點放在面層、填土、波紋鋼結構和基礎等結構層的幾何模型上［3］。為了簡化波紋鋼結構，可以采用剛度等效方法將其簡化為平板結構，并建立簡化的3D波紋鋼箱型橋梁幾何模型。

2.2生成有限元模型

幾何模型在計算分析中并不能直接使用，因為需要先定義單元屬性并進行網格劃分。通過轉換生成有限元模型，可以進行一系列結構分析計算。

2.2.1定義單元屬性

由于波紋鋼箱型橋梁是一個三維實體結構，為了獲得較好的分析效果，選擇SOLID45單元進行建模。SOLID45單元的每個節點均具有三個坐標軸方向的平動自由度，并且支持正交各向異性材料屬性［4］。此外，SOLID45單元還可以模擬3D實體結構的各種力學行為。

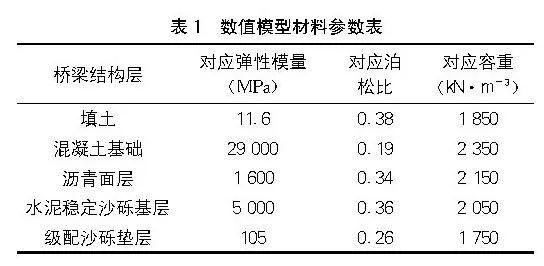
在波紋鋼箱型橋梁數值模型中，使用剛度等效方法對波紋鋼結構進行建模。該方法將波紋鋼結構的幾何各向異性轉換為材料的各向異性。建模時需要輸入的材料參數，包括三個主向的彈性模量、泊松比和剪切模量，總共需要9個參數。然而，在表1中，只給出了5個參數。因此，需要根據實際建模方式，確定單元坐標系與建模采用的坐標系之間的關系，以確定其他參數的輸入方式。

2.2.2網格劃分及賦予單元屬性

本文采用LESIZE命令控制網格劃分的單元尺寸，并使用VATT命令為幾何模型的各個結構賦予材料屬性。同時，采用掃描網格劃分方法，從源面網格掃描生成整個體結構的六面體單元。圖1展示了單跨波紋鋼箱型橋梁的數值模型，其尺寸為28.35 m×24 m×6.482 m，總共生成了178 384個節點和169 224個單元。

2.2.3接觸設置

為了簡化波紋鋼箱型橋梁數值模型中不同結構層間接觸狀態的計算過程，僅考慮了填土與波紋鋼結構的接觸。采用剛-柔面接觸模型，分別為鋼板一側和填土一側定義了不同的有限元單元：鋼板一側接觸面通過TARGE170單元表示；填土一側接觸面通過CONTA173單元表示。這兩個接觸面使用相同實常數進行識別，并設置摩擦系數為0.28。這一設定能夠準確反映真實物理行為，并提供精確的計算結果。

2.3邊界約束及荷載施加

全約束地面的固定可以防止橋梁晃動和滑動。對端面的約束是為了滿足填土的限制條件，防止橋梁在X方向上發生過度變形或失穩。同樣，對橋梁的兩側也要進行約束，以防止Z方向上的位移。此外，還需要考慮端墻對橋梁的影響，并對橋梁兩端的波紋鋼結構進行豎向位移的約束。

為了對單跨波紋鋼箱型橋梁進行加載測試，進行了三種不同荷載工況下的靜載試驗。這三種荷載工況分別是：（1）工況Ⅰ：雙后輪對右側拱腳施加荷載；（2）工況Ⅱ：雙后輪對拱頂施加荷載；（3）工況Ⅲ：雙后輪對左側拱腳施加荷載。每個加載點位的持續時間為20 min。采用實體單元建模的數值模型，在模型頂部的節點區域施加了相應車輛前后輪的荷載以進行加載。

3波紋鋼截面應變與位移有限元結果分析

3.1縱向應變結果分析

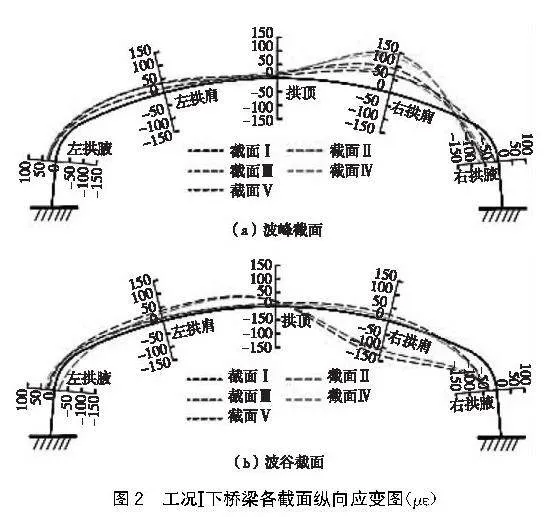
通過進行有限元數值模擬分析，可以計算得到箱型波紋鋼橋梁結構在關鍵截面波峰和波谷處的應變增量，并且還可以得到拱頂處的豎向位移增量，借此分析該類型結構在承受力和變形方面的特性。通過對單跨波紋鋼箱型橋梁各截面測點處的縱向應變有限元模擬進行分析，得出了如圖2～4所示的結果。

由圖2可知，在工況Ⅰ下，車輛受到雙后軸對右拱腳的作用以及前軸對右拱肩附近的作用，導致波紋鋼截面在右拱肩處產生較高的縱向應變增量。具體而言，受到輪壓作用的截面Ⅱ顯示出最大的應變增量，分別為142 με和-131 με。與之相比，位于端墻附近的截面Ⅰ受力較小，產生的應變增量為64 με和-111 με。右拱肩的波峰和波谷在受到前輪壓力時呈現相反的受力狀態，而雙后輪作用附近的右拱腋一直處于受壓狀態。由于波紋鋼結構的柔性特點，當一側受到加載力時，遠離荷載作用一側的左拱腋至拱頂位置也會發生一定程度的受力變形。在變形協調作用下，整體上不同環向截面產生的縱向應變值相差不大，并且主要呈現受拉狀態。

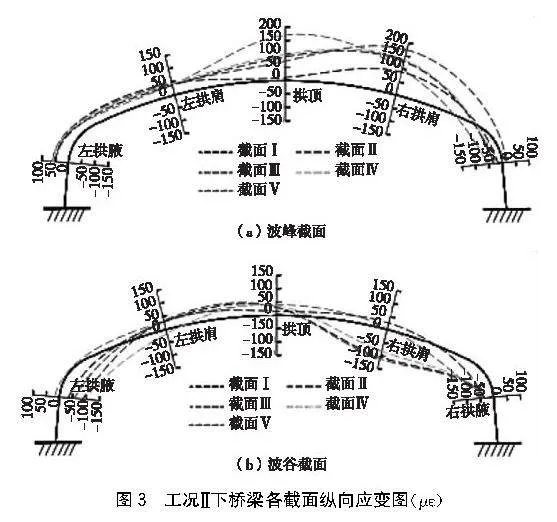
在工況Ⅱ下，當車輛的雙后軸和前軸作用于拱頂和左拱肩附近時，發現縱向應變增量最大的位置位于右拱肩，如圖3所示。這種現象與前一工況下相似，右拱肩處的縱向應變增量為172 με和-112 με（截面Ⅱ），以及87 με和-105 με（截面Ⅰ）。這很可能是拱背填土的影響引起的。

當荷載施加于結構上時，波紋鋼發生變形后會改變土壓力的分布，這種狀態可能會持續一段時間。在受到車輛雙后輪直接作用的影響下，拱頂位置產生的縱向應變增量比前一工況下有了顯著增加，特別是波峰截面的應變增長現象尤為明顯。左拱肩位置的受力變形也發生了重新分布，不再主要處于受拉狀態。在這個位置，波峰和波谷處產生了近似相等但大小相反的應變增量，這說明左拱肩位置主要是受到彎矩作用。

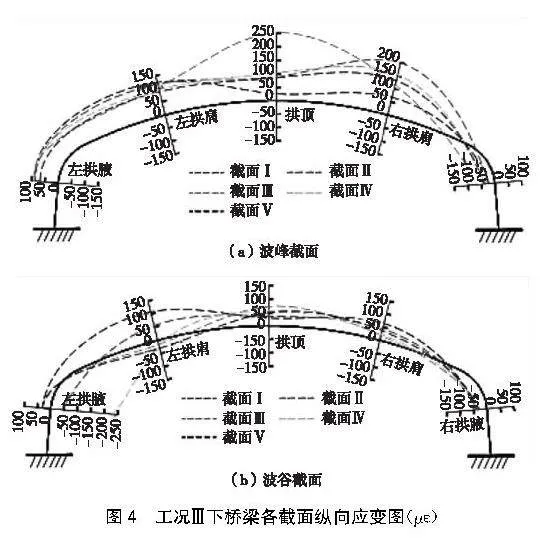
根據工況Ⅲ的試驗結果，當車輛從波紋鋼橋梁上駛離時，圖4顯示了雙后軸對左拱腳的作用，導致前軸離開橋面。與工況Ⅰ和工況Ⅱ相似，縱向應變的變化趨勢也相似。拱頂、兩側拱肩以及左拱腋位置的應變增量都呈不同程度的增長，這再次驗證了結構變形累積作用的影響。與工況Ⅰ相比，車輛離開加載位置后，前一工況加載所產生的應變增量并沒有逐漸減小并恢復原狀。相反，從工況Ⅰ到工況Ⅲ，車輛經過的各個加載點的應變增量逐漸增加。

3.2橫向應變結果分析

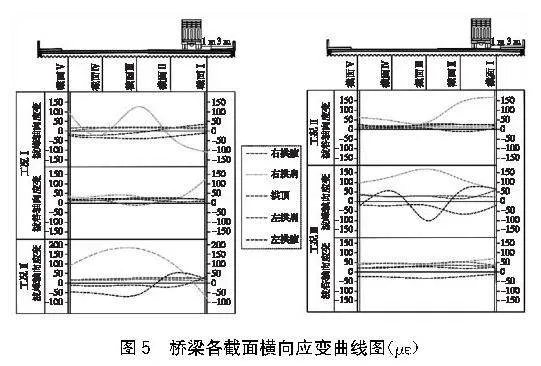
如圖5所示的單跨波紋鋼箱橋各截面在橫向應變增量方面的分布情況，經過數據分析，得出以下結論：（1）橋梁各截面在橫向方向上的應變增量整體上相似，但截面Ⅲ的應變增量相對較大，由中心逐漸減小至兩側；（2）截面Ⅰ和Ⅴ靠近端墻，因此其橫向應變數值最小；（3）與縱向應變相比，橫向應變增量對車輛荷載位置變化的影響較小；（4）右側拱肩位置對荷載作用及其位置變化更敏感。不論不同工況如何，各截面的橫向應變變化規律基本上相似，總體上呈現拉應變增量為主。

3.3位移結果分析

圖6展示了單跨箱型波紋鋼橋梁結構拱頂的位移分布情況。從圖6中可以看出，在三種不同的加載條件下，拱頂的豎向位移分布規律是一致的，呈現出左高右低的變形特征。

在車輛直接作用下，拱頂的右側半幅路面主要產生向下的豎向位移。當雙后輪作用于拱頂位置時，截面Ⅱ產生最大的豎向位移，達到-0.72 mm，而截面Ⅰ和Ⅲ的位移值稍小。另一方面，截面Ⅳ產生向上的位移。在該位置附近的波紋鋼結構上，拱擠壓土體。值得注意的是，截面Ⅳ和Ⅴ在三種工況加載條件下產生的位移數值之間相差不大，不像截面Ⅰ、Ⅱ和Ⅲ產生的豎向位移值差異明顯。這是由于加載位置的影響，靠近加載位置的各截面在不同加載條件下位移值變化較為顯著。

4波紋鋼箱型截面內力有限元結果分析

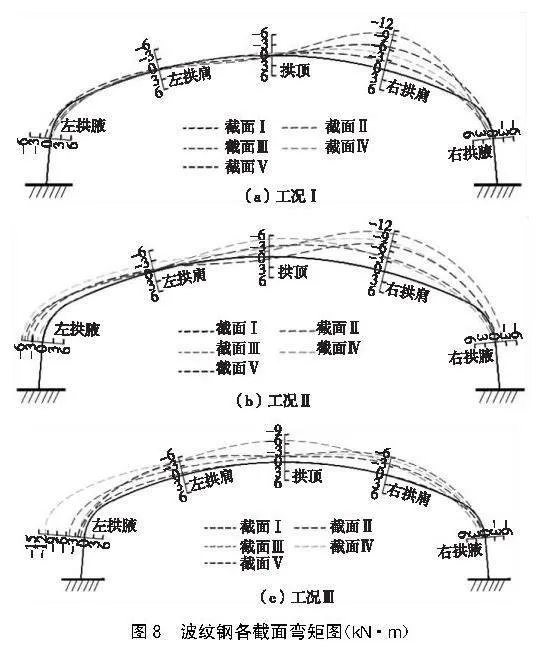
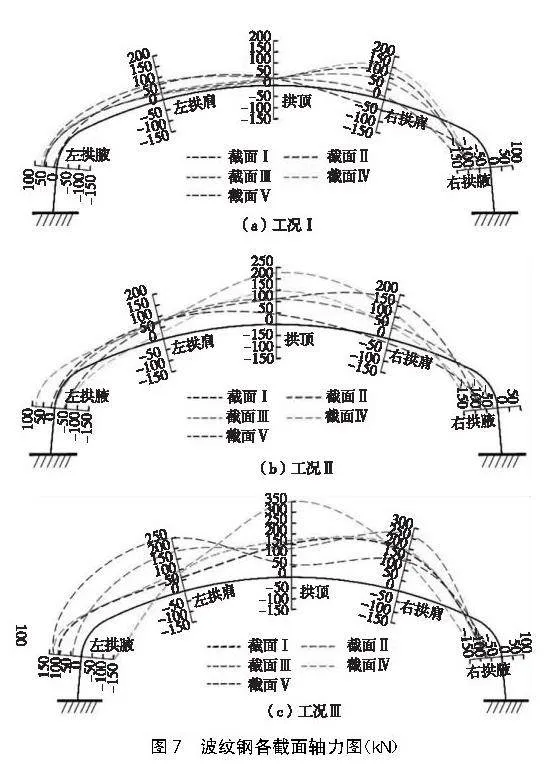
單跨波紋鋼箱型橋梁在車輛荷載作用下的截面軸力、彎矩內力分布如圖7、圖8。

在工況Ⅰ下，車輛的雙后軸作用于拱腳，而前軸作用于拱肩附近，這導致荷載作用點一側的拱腋受到壓力，同時拱肩位置向土體側發生彎曲變形，產生最大的軸向應力和彎曲應力。然而，非荷載作用一側的拱頂、拱肩和拱腳主要受到拉力，產生的彎曲應力較小。在輪壓作用截面上，截面Ⅰ靠近端墻，受到端墻約束的影響較大，而截面Ⅱ受到的端墻影響較小。

經分析發現，工況Ⅱ和工況Ⅲ下波紋鋼箱型橋梁的內力分布與工況Ⅰ下具有相似規律。然而，不同之處在于車輛行駛過程中，輪壓下方測點所受的軸力和彎矩逐漸增大。主要承受的是拉應力和正彎矩，同時截面內力呈逐漸對稱的分布形態，這很可能是變形逐漸積累的結果。在不同工況下，最大彎矩分別出現在工況Ⅱ的Ⅰ截面、工況Ⅰ的Ⅱ截面和工況Ⅲ的Ⅳ截面，而最大軸力出現在工況Ⅲ下。三種工況下的最大軸力和彎矩分別為48.97 kN和12.64 kNm，這證明了波紋鋼箱型橋梁在承受彎矩的同時，也會承受較大的軸力，兩者都是不可忽視的。

5結語

本研究采用數值分析的方法，對單跨波紋鋼箱型橋梁在不同荷載作用下的變形和受力特性進行了分析。在考慮了土體恒載和車輛活載的情況下，得出以下結論：

（1）橋梁在荷載作用下受到的軸力和彎矩較大，特別是在車輛活載作用下，這對于橋梁的結構安全性和穩定性具有重要影響。

（2）拱頂位移是衡量橋梁變形程度的重要指標之一。

在車輛活載的作用下，拱頂位移較大，這可能會影響橋梁的使用壽命和結構完整性。

（3）通過對橋梁截面的應變和內力變化進行深入研究發現，在荷載作用下，橋梁截面承受的應變和內力較大，需要進行合理的材料選取和結構設計，以保證橋梁的安全和穩定性。

參考文獻：

［1］2020年我國交通運輸行業發展統計公報發布［J］.隧道建設（中英文），2021，41（6）：963.

［2］李百建，符鋅砂，朱良生.基于車-橋耦合的鋼波紋板動力分析方法對比研究［J］.公路工程，2019，44（6）：1-8，32.

［3］孫偉明，劉保東，孫海波，等.采用正交試驗法進行波紋鋼箱涵應力和變形對加勁肋參數的敏感性分析［J］.公路，2022，67（1）：139-145.

［4］陳望祺.帶有減載板的覆土波紋鋼拱橋受力性能試驗研究［D］.北京：北京交通大學，2020.

作者簡介：童凱（1990—），工程師，研究方向：路橋工程。