星載天線陣列動力學分析及優化設計

姚文旭,熊一帆,王光輝,宮超越,趙騰山

(上海航天電子技術研究所,上海 201109)

多路收發天線系統是通訊及遙感衛星中重要的載荷設備,具有接收、發射電磁信號,在軌信息處理等綜合功能。星載設備在測試、發射、在軌運行過程中會經歷多種苛刻的載荷環境,如沖擊、過載、寬帶隨機振動和低頻激勵等,振動過程產生的應力、位移等極易造成儀器設備關鍵部位結構性損傷,嚴重時將引起整星失效[1-3]。由此可知,研究星載設備的振動力學問題對提高結構的可靠性至關重要。

隨著計算力學的快速發展,使用有限元軟件在時域或頻域內進行結構的動力學仿真已得到廣泛應用。在星載設備的結構設計中,有必要利用有限元軟件進行振動分析,以便設計師在產品研發早期發現結構設計中的不足,找出優化方案,以縮短新品研制周期[4]。

長期以來,多路收發天線系統主要用于地面通信,但隨著衛星通信的快速發展,該類設備逐漸成為重要的星載設備。很多學者對一般星載設備做了動力學分析研究[5-6],但對多路收發天線陣列的力學分析及結構優化的研究較少。本文從結構動力學分析出發,發現了原結構設計中的風險并進行優化設計,最終滿足了儀器設備對結構安全性的要求。本文中采用的分析和優化方法,對于同類模型設計具有重要的參考意義。

1 天線陣列模型設計

綜合考慮天線電學性能、結構質量等因素,模型采用安裝基板-支撐框架設計形式。安裝基板采用輕質鋁合金材料,天線使用L型角件固定于基板一側,儀器設備按照設計要求分布在基板另一側。為了便于地面轉場測試,整機結構固定于可移動不銹鋼推車上,如圖1所示。

圖1 四路天線地面測試模型

2 動力學基本原理

2.1 模態分析

多自由度系統的動力學方程為:

(1)

固有特性與外載荷無關,且阻尼對固有頻率和固有振型影響不大,因此在進行模態分析時,不考慮阻尼和外力的影響,即C=0,f(t)=0,式(1)變為:

(2)

該方程的解可以用正弦振動的形式表示為x=Xsin(ωt+θ),其中X為振幅,ω為圓頻率,t為時間,θ為初相位,代入式(2)可得特征方程為:

[K-ω2M]X=0

(3)

式(3)具有非零解的充要條件是:

|K-ω2M|=0

(4)

求解行列式(4)可得特征值的算術平方根ωi(i=1,2,…,n),即結構的第i階固有頻率;代入式(3)中求出特征向量ψi(i=1,2,…,n),即結構的第i階模態振型。

2.2 頻率響應分析

在頻率響應分析中,載荷是通過頻率、振幅和相位所確定的正弦波,式(1)可以轉變為:

(5)

式中:p為簡諧力的幅值。

式(5)中,等號右邊表示圓頻率為ω的簡諧力,與結構的固有頻率ωn無關。簡諧力的幅值p作為靜態載荷施加給結構,則結構的靜態位移δst=p/k,其中k為剛度。

無阻尼情況下,結構動態位移響應的幅值A與δst的比值λ稱為動態放大系數:

(6)

當激勵頻率接近結構的固有頻率時,ω/ωn趨近1,式(6)分母趨近0,導致動態放大系數將無窮大,表現為結構的動態響應振幅非常大,即發生共振現象。

使用模態法進行頻率響應分析時,至少應保留最高激勵頻率2～3倍的所有模態。模態頻率響應盡管存在模態截斷會造成一定誤差,但計算量將大幅減小,計算效率顯著提高[7-8]。

3 有限元建模及動力學分析

3.1 有限元建模

建模前需對結構進行理想化處理,刪除小孔、凹槽、倒角等容易產生應力集中的幾何特征。將電容器、激光器、透射鏡和反射鏡等結構劃分為正六面體單元,安裝板劃分為四面體單元。因為本文重點是研究安裝板的結構特性對天線陣列的影響,所以將天線結構簡化成集中質量單元并賦予相應慣量,使用彈性單元與安裝板連接,天線有限元模型如圖2所示。在底板中心位置創建節點,并與邊沿固定孔建立剛性連接RBE2,便于施加邊界條件和動態載荷。

圖2 有限元模型

3.2 模態分析

選用NX 11.0中的實特征值解算方案進行天線陣列的模態分析。約束安裝板四周6個自由度,采用Block Lanczos法進行模態提取,得到的前6階模態頻率見表1。

表1 結構前6階模態頻率

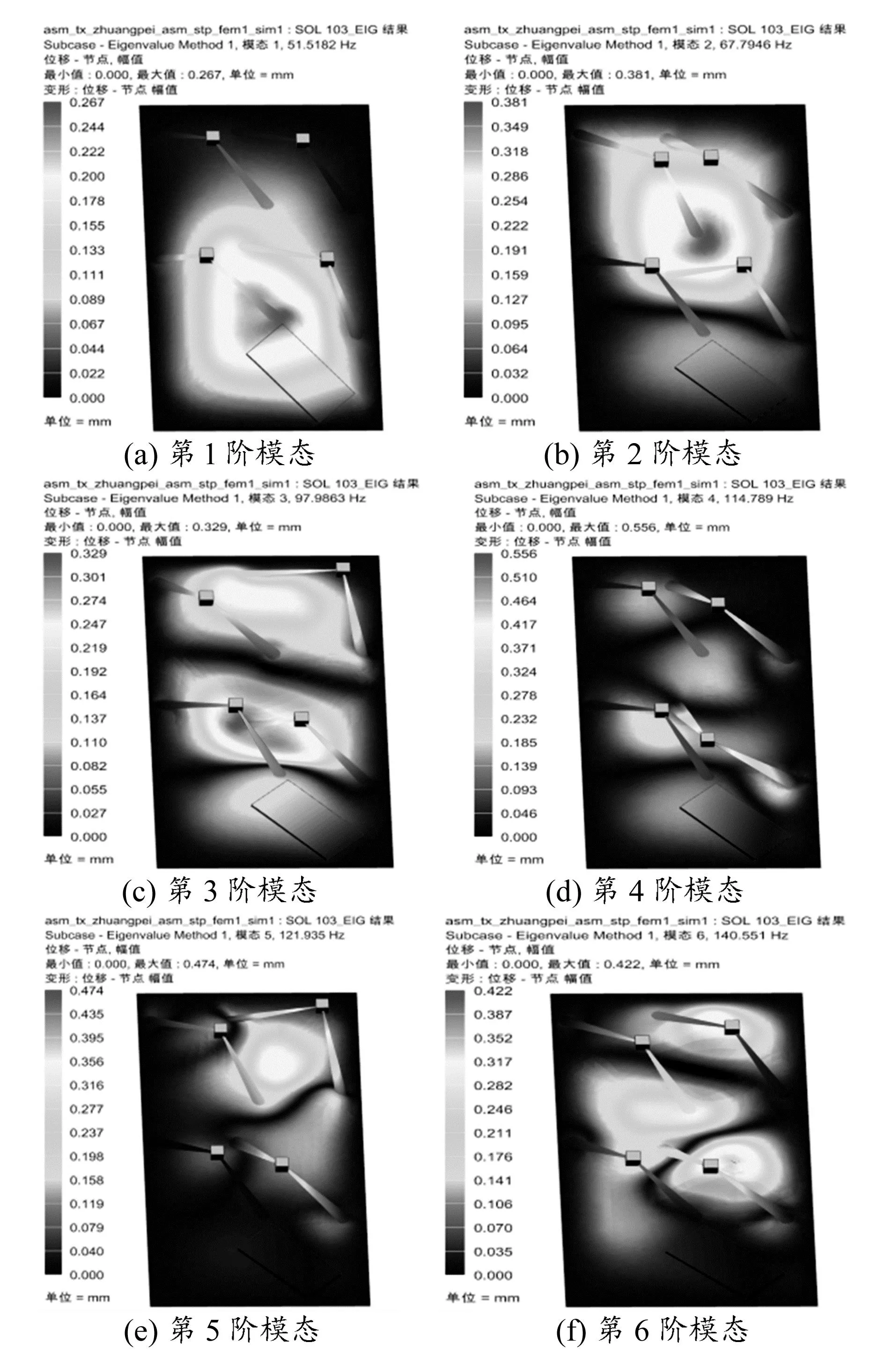
圖3 前6階振型圖

3.3 頻響分析

選用響應動力學解算方案進行正弦響應分析。一般單機正弦振動試驗條件見表2,本次加載的是最嚴苛的鑒定級載荷,頻率從5 Hz到100 Hz,載荷輸入方向分別為平行安裝板方向(X、Y向)和垂直安裝板方向(Z向)。

表2 一般單機正弦振動試驗條件

正弦振動中位移方程為D=D0sin(ωt),微分后可得加速度方程A=-ω2D0sin(ωt),加速度幅值與位移幅值關系為|A|=ω2|D|。本次試驗位移和加速度的正弦振動譜線如圖4所示,位移和加速度幅值分別為11.04 mm和10.0g。

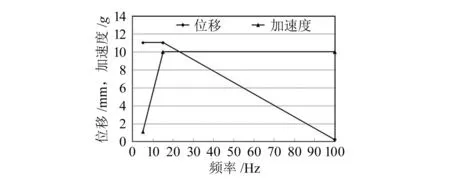
圖4 正弦振動譜線

由模態分析結果可知,模型第26階模態頻率為301.3 Hz,約是最高激勵頻率的3倍,本文選取前30階模態進行分析,得到各方向下結構最大正弦響應結果,見表3。

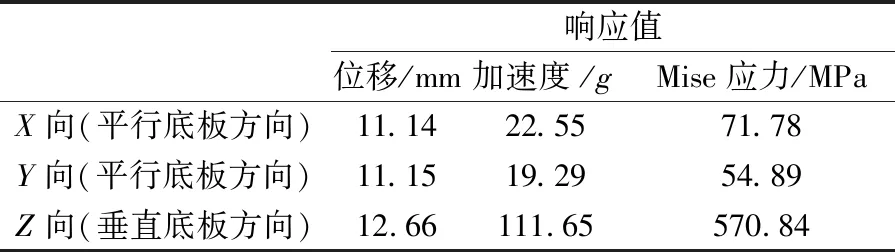
表3 陣列天線正弦響應最大值

對于星載設備的振動響應來說,最大應力直接決定結構是否發生強度破壞。平行于底板方向的X向和Y向應力值均不超過鋁合金屈服強度275 MPa,滿足結構安全要求。垂直底板方向(Z向)的最大應力為570.84 MPa,遠超鋁合金屈服強度,結構存在屈服破壞的風險,響應如圖5所示。為了保證結構絕對安全,必須對此模型進行結構加固。

圖5 Z向正弦響應云圖

四路天線質心處的加速度和位移響應曲線如圖6所示,峰值范圍分別為45～55 Hz和60～75Hz,分別與結構的1階頻率和2階頻率對應,這是因為外界激勵與結構本體頻率重合后誘發共振,產生了較大的振動響應。

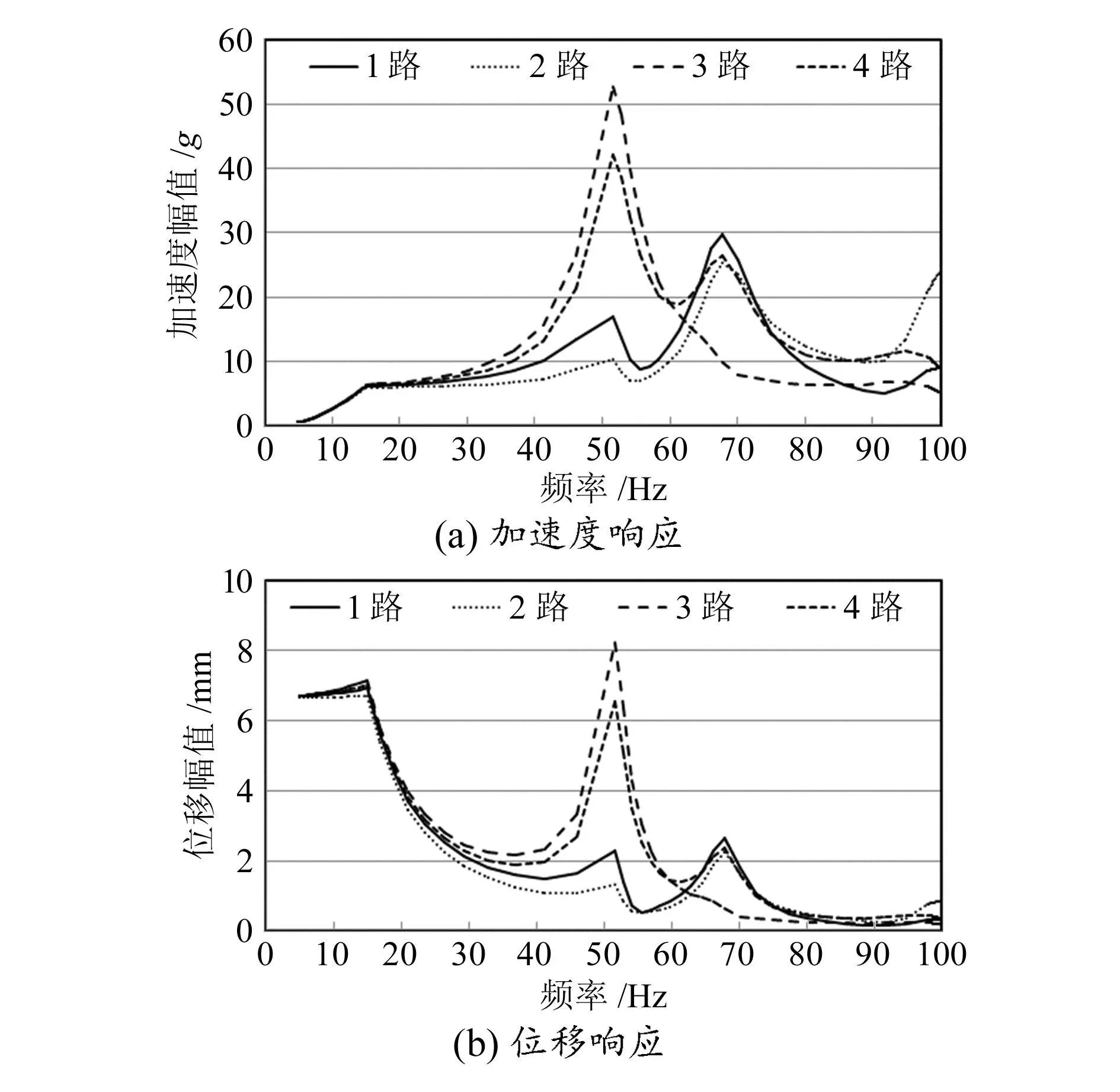
圖6 正弦振動響應

4 結構優化設計

4.1 安裝板結構優化

針對安裝板強度較低問題,在不改變天線陣列空間布局、不影響電性能的前提下,考慮在安裝板中央區域布置加強梁和增大底板厚度的方式來提高結構剛度。具體的修改如下:

1)增大板厚。由于底板背部連接大量器件,約占總質量的46%,底板厚度只有5 mm,底板較薄,易發生彎曲變形。因此,將底板厚度增大為7 mm。

2)布置加強梁。通過在底板變形較大區域布置斜向和橫向加強梁,增強底板抵抗變形的能力。

3)開減重孔。為了避免底板質量變化太大,在底板沒有安裝器件的位置開減重孔。

底板優化前后模型對比如圖7所示,優化后模型質量為82.5 kg,與原模型相比質量增加了9.7%。

4.2 模態分析

優化后結構的有限元網格劃分方法和邊界條件設置與原模型保持一致。優化前后頻率對比見表4,前6階頻率較原結構提高了48.2%～170.3%,模型整體剛度得到有效加強。其中基頻是原來的2.7倍,大于100 Hz,達到星載設備基頻要求。

表4 優化前后頻率對比

優化后結構的前6階振型如圖8所示,第1階振型表現為安裝板的1階彎曲,其余振型均為PCB板彎曲,底板變形較大問題得到有效解決。

圖8 優化后結構前6階振型圖

4.3 正弦響應分析

正弦激勵下,結構優化前后最大響應值見表5。結構最大位移與原結構相比減少了1.43 mm,降幅為11.3%。而最大加速度降低明顯,從111.65g降低到24.56g,降幅達78.0%。結構優化后von Mise應力最大為169.87 MPa,與原模型570.84 MPa相比降低了70.24%,結構應力遠小于鋁合金屈服強度,滿足結構強度要求。

表5 模型優化前后正弦分析最大響應值

圖9為優化后結構Z向輸出響應云圖,最大應力和最大位移發生位置轉移,底板彎曲和應力集中現象得到有效改善,驗證了優化方案的有效性。

圖9 優化后Z向輸出響應云圖

四路天線質心的正弦響應曲線如圖10所示,加速度響應和位移響應最大值分別為11.6g和6.66 mm,與原結構相比降幅達78%和18.8%,天線搖擺現象得到有效控制。

5 結束語

本文基于有限元法建立了星載天線的動力學模型,并進行了相應的力學分析,發現結構基頻較低且存在強度破壞的風險。經結構優化后,模型質量變化較小,而結構基頻顯著增大、輸出響應明顯減小,滿足了結構安全要求。本文所采用的分析方法,可為同類結構的優化設計提供參考與指導。