基于模糊變結(jié)構(gòu)補(bǔ)償?shù)臋C(jī)械臂運(yùn)動路徑避障規(guī)劃算法

李井林

(江蘇聯(lián)合職業(yè)技術(shù)學(xué)院蘇州工業(yè)園區(qū)分院,江蘇 蘇州 215123)

工業(yè)機(jī)器人作為高端機(jī)械裝置,可應(yīng)用于實際工業(yè)生產(chǎn),提升生產(chǎn)效率[1]。隨著人工智能領(lǐng)域技術(shù)的進(jìn)步,大量程序、算法被用于機(jī)械臂的設(shè)計與制造,從而有效地降低了復(fù)雜程度,縮減了生產(chǎn)監(jiān)測領(lǐng)域的人工成本[2]。機(jī)械臂本身具備的自由度特性能夠保證機(jī)械臂在不同環(huán)境中高效地完成任務(wù),但是環(huán)境的復(fù)雜性會給機(jī)械臂操作帶來難度,有效地對機(jī)械臂路徑進(jìn)行避障規(guī)劃就成為機(jī)械臂操作過程中最為重要的一個環(huán)節(jié)[3]。

文獻(xiàn)[4]提出基于單目視覺的多種群粒子群機(jī)械臂路徑規(guī)劃算法,通過模型位置估計法獲取目標(biāo)位置,利用粒子群算法計算目標(biāo)位置向量,獲取機(jī)械臂的最優(yōu)運(yùn)動角度,實現(xiàn)路徑的避障規(guī)劃。該算法由于未能在路徑規(guī)劃前對機(jī)械臂進(jìn)行具體的動力學(xué)分析,因此該算法的路徑規(guī)劃效果差。文獻(xiàn)[5]提出基于碰撞檢測的空間冗余機(jī)械臂避障路徑規(guī)劃,該算法通過對機(jī)械臂空間占位關(guān)系的描述,判斷機(jī)械臂運(yùn)動軌跡與球體之間是否存在障礙;通過粒子群算法對目標(biāo)函數(shù)進(jìn)行求解,獲取機(jī)械臂最佳運(yùn)動軌跡,實現(xiàn)機(jī)械臂的路徑規(guī)劃。但是該算法在建立位姿擾動函數(shù)時存在問題,因此該算法規(guī)劃的路徑較長。文獻(xiàn)[6]提出基于改進(jìn)的RRT*-connect算法的機(jī)械臂路徑規(guī)劃,首先通過梯度下降法對搜索路徑進(jìn)行優(yōu)化,然后通過優(yōu)化結(jié)果實現(xiàn)目標(biāo)路徑的規(guī)劃。因為該算法在搜索目標(biāo)路徑時存在誤差,所以該算法的路徑規(guī)劃時間較長。

為解決上述機(jī)械臂避障路徑規(guī)劃過程中存在的問題,本文提出了基于模糊變結(jié)構(gòu)補(bǔ)償?shù)臋C(jī)械臂運(yùn)動路徑避障規(guī)劃算法。

1 機(jī)械臂模糊力矩控制方法

1.1 機(jī)械臂動力學(xué)分析

設(shè)定機(jī)械臂移動坐標(biāo)為Q(x,y),關(guān)節(jié)連接點分別為O、A、B,運(yùn)動角度為θ,以此建立機(jī)械臂的運(yùn)動模型:

M=OθiAθiBθi/Q(xi,yi)

(1)

式中:M為建立的機(jī)械臂運(yùn)動模型,Oθi、Aθi、Bθi為關(guān)節(jié)連接點運(yùn)動角度。

基于建立的機(jī)械臂運(yùn)動模型,假設(shè)機(jī)械臂運(yùn)動的位置表示為ω(t),使用拉格朗日方程[7]對機(jī)械臂進(jìn)行動力學(xué)分析:

(2)

設(shè)定機(jī)械臂連桿長度為C1、C2、C3,質(zhì)點為z1、z2、z3,具體結(jié)構(gòu)如圖1所示。

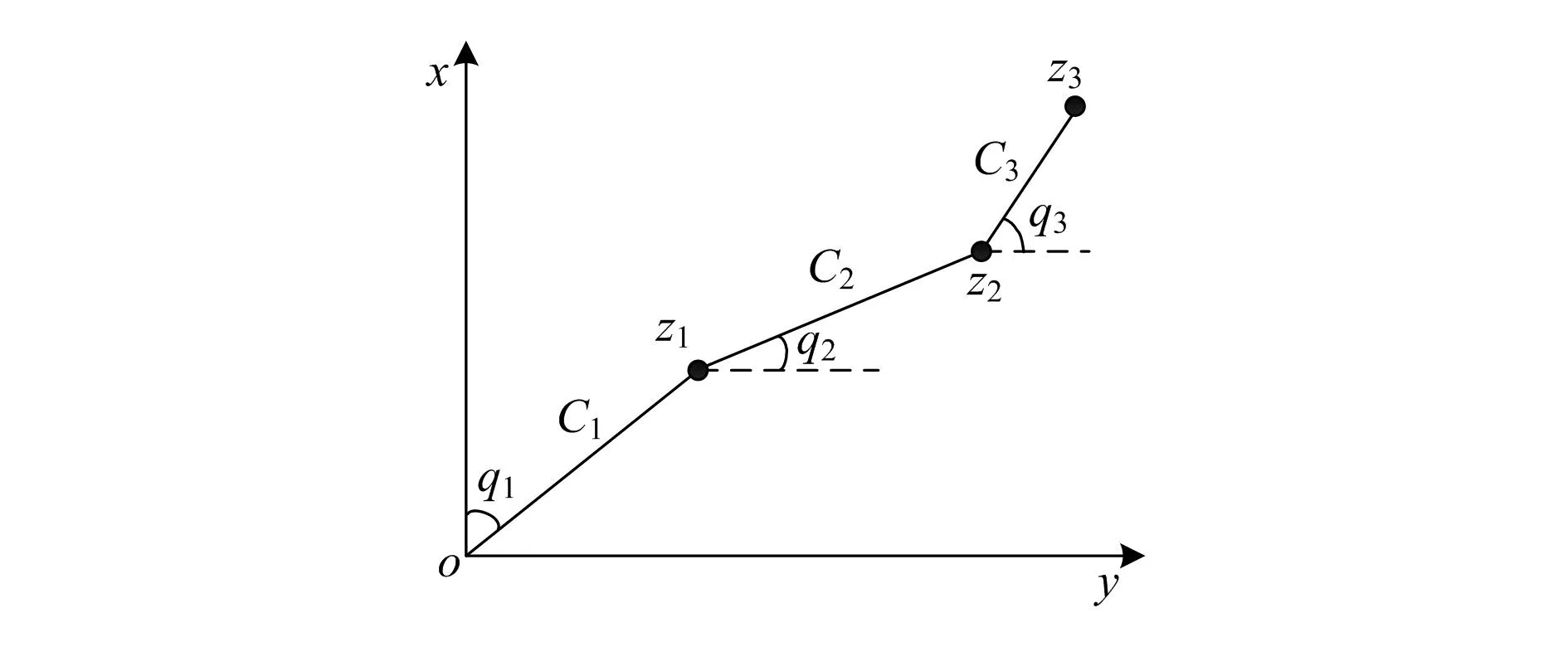
圖1 機(jī)械臂質(zhì)點坐標(biāo)圖

1.2 機(jī)械臂模糊力矩控制

因為機(jī)械臂的活動范圍可以自由調(diào)整以適應(yīng)不同的工作環(huán)境,使其具有較高的靈活性,所以需要依據(jù)上述分析結(jié)果獲取機(jī)械臂活動的控制規(guī)律:

(3)

依據(jù)上述獲取的機(jī)械臂[8]運(yùn)動規(guī)律,對機(jī)械臂力矩進(jìn)行補(bǔ)償處理。設(shè)定機(jī)械臂模糊部分為η,從而獲得機(jī)械臂理想軌跡各項參數(shù)狀態(tài):

(4)

依據(jù)上述計算結(jié)果建立機(jī)械臂不確定部分的有界包絡(luò)函數(shù)‖η‖[9]:

‖η‖≤β1+β2‖x‖

(5)

式中:β2為機(jī)械臂不確定部分對總體不確定性的影響程度,‖x‖為機(jī)械臂狀態(tài)方程。x的計算公式為:

x=h(x)+Iη

(6)

式中:x為機(jī)械臂的狀態(tài)變量,h、I為機(jī)械臂力矩矩陣的兩種形式。

為規(guī)劃機(jī)械臂運(yùn)動模型的全局穩(wěn)定性,需建立Lvapunov函數(shù)重新獲取機(jī)械臂的變結(jié)構(gòu)運(yùn)動規(guī)律:

(7)

式中:φ為建立的Lvapunov函數(shù),T為迭代函數(shù),b為變結(jié)構(gòu)運(yùn)動規(guī)律,Q為變結(jié)構(gòu)控制器參數(shù)。

最后通過上述獲取的機(jī)械臂的變結(jié)構(gòu)運(yùn)動規(guī)律,完成機(jī)械臂力矩控制。

2 基于Q-learning算法的機(jī)械臂運(yùn)動路徑避障控制

2.1 算法描述

設(shè)定學(xué)習(xí)變量為α、最佳取值范圍為[0,1]、智能體為γ、平衡回報為αt、新循環(huán)狀態(tài)為Zt+1,智能體γ可以在機(jī)械臂運(yùn)動中進(jìn)行更新循環(huán)狀態(tài)的操作[10]。更新循環(huán)狀態(tài)過程如式(8)所示:

Q(Zt,γt)→(1-τ)Q(Zt,γt)+τ[αt+α·maxQ(Zt+1,γt)]

(8)

式中:Q(zt+1,γt)為更新后的循環(huán)狀態(tài)值,其中γt為智能體的狀態(tài);τ為學(xué)習(xí)因子;zt為原始循環(huán)狀態(tài)。

為了獲得機(jī)械臂在高維連續(xù)空間中的最佳運(yùn)動軌跡,并對其與實際軌跡進(jìn)行比較和計算反饋誤差,可以引入BP神經(jīng)網(wǎng)絡(luò)函數(shù)。通過訓(xùn)練神經(jīng)網(wǎng)絡(luò),能夠?qū)W習(xí)并擬合機(jī)械臂在不同狀態(tài)下的運(yùn)動模式。一旦訓(xùn)練完成,可以將當(dāng)前的機(jī)械臂狀態(tài)作為輸入,使用BP神經(jīng)網(wǎng)絡(luò)函數(shù)來預(yù)測最佳軌跡值。然后,通過對比實際軌跡和預(yù)測軌跡,計算它們之間的差異,從而得到反饋誤差信息[11]。這些反饋誤差有助于評估機(jī)械臂運(yùn)動模型的準(zhǔn)確性和精度,并指導(dǎo)改進(jìn)控制策略以提高運(yùn)動性能。因此,引入BP神經(jīng)網(wǎng)絡(luò)函數(shù)可以幫助優(yōu)化機(jī)械臂的運(yùn)動控制,并提升其精確度和性能。機(jī)械臂運(yùn)動軌跡的反饋誤差值計算公式為:

Δν=τ[μ(Zt,γt)+αmaxQ(Zt+1,γt)]-Q(Zt,γt)

(9)

式中:Δν為機(jī)械臂的反饋誤差值,μ為激勵系數(shù)。

2.2 Q值更新

基于Q-learning算法對機(jī)械臂運(yùn)動軌跡進(jìn)行優(yōu)化時,可將獲取的Q函數(shù)作為評價指標(biāo),辨識輸出路徑的理想狀態(tài)。建立Q值表并對其進(jìn)行初始化,通過R值確定機(jī)械臂下一運(yùn)動狀態(tài),使用BP神經(jīng)網(wǎng)絡(luò)完成Q值更新。設(shè)定神經(jīng)元輸入向量為xi,對應(yīng)權(quán)重為ωi,選擇適當(dāng)?shù)募せ詈瘮?shù)計算機(jī)械臂Q值:

(10)

式中:yi為神經(jīng)網(wǎng)絡(luò)模型輸出結(jié)果;ωik為權(quán)重系數(shù),其中k為常數(shù)項。基于上述結(jié)果,使用神經(jīng)網(wǎng)絡(luò)的最佳逼近值對算法Q值進(jìn)行更新,具體計算公式如式(11)所示:

Q(Zt+1,γt+1)=τQ(Zt,γt)+τ·ωik[αt+1+μt· maxQ(Zt,γt)]

(11)

式中:Q(Zt+1,γt+1)為最終的Q值更新值,μt為獎勵值。當(dāng)機(jī)械臂運(yùn)動狀態(tài)從Zt轉(zhuǎn)向Zt+1時,可獲取相應(yīng)的μt,而學(xué)習(xí)因子也會隨著Q值迭代效率的提高而加速收斂。

2.3 路徑避障規(guī)劃

機(jī)械臂移動路徑可看作坐標(biāo)系的移動過程,坐標(biāo)轉(zhuǎn)換中,路徑規(guī)劃不僅要考慮機(jī)械臂連桿長度與水平夾角的大小,還要對機(jī)械臂關(guān)節(jié)角度以及連桿偏距進(jìn)行必要考量。設(shè)定機(jī)械臂空間范圍的位姿變換矩陣為W,機(jī)械臂關(guān)節(jié)旋轉(zhuǎn)角度為σi,連桿偏距為di,可得計算公式為:

W=

(12)

式中:Li為機(jī)械臂連桿長度,ψi為機(jī)械臂連桿與關(guān)節(jié)軸線的夾角。

設(shè)定機(jī)械臂移動鏈條為P,且該鏈條由若干機(jī)械臂節(jié)點構(gòu)成。

在求解封閉空間機(jī)器人的最佳運(yùn)動軌跡時,當(dāng)機(jī)器人的關(guān)節(jié)軸與一點相交,可以利用高維方程對其進(jìn)行降維,以求出最佳的路徑。

為了保證機(jī)械臂整體運(yùn)動的連續(xù)性,首先對機(jī)械臂進(jìn)行處理,包括切斷機(jī)械臂節(jié)點P0,并將其移動到坐標(biāo)零點,設(shè)定關(guān)節(jié)的自由度P2=0,計算各關(guān)節(jié)的轉(zhuǎn)向角和角度變量。通過這些處理,可以將機(jī)械臂的基準(zhǔn)位置設(shè)定在坐標(biāo)零點,便于后續(xù)計算和優(yōu)化。為了確保機(jī)械臂運(yùn)動的連續(xù)性,需要考慮關(guān)節(jié)的自由度和關(guān)節(jié)旋轉(zhuǎn)距離。通過設(shè)定適當(dāng)?shù)淖杂啥群陀嬎愫侠淼霓D(zhuǎn)向角和角度變量,可以確定機(jī)械臂在各個方向上的運(yùn)動范圍和關(guān)節(jié)之間的角度差。這樣可以保證機(jī)械臂的運(yùn)動在各個關(guān)節(jié)之間的協(xié)調(diào)性和連貫性。

依據(jù)上述分析結(jié)果,使用Q-learning算法對獲取的路徑進(jìn)行誤差校正,合理躲避路線上的障礙物,依據(jù)機(jī)械臂Q值狀態(tài)獲取路徑解分布規(guī)律,通過迭代計算完成機(jī)械臂最佳路徑的規(guī)劃[12]。

3 實驗

為了驗證上述機(jī)械臂避障路徑規(guī)劃方法的整體有效性,需要對此方法進(jìn)行測試。實驗用機(jī)械臂如圖2所示,運(yùn)動路徑如圖3所示。

圖2 實驗用機(jī)械臂

圖3 機(jī)械臂的運(yùn)動路徑

分別采用基于模糊變結(jié)構(gòu)補(bǔ)償?shù)臋C(jī)械臂運(yùn)動路徑避障規(guī)劃算法(本文方法)、基于單目視覺的多種群粒子群機(jī)械臂路徑規(guī)劃算法(文獻(xiàn)[4]方法)、基于碰撞檢測的空間冗余機(jī)械臂避障路徑規(guī)劃(文獻(xiàn)[5]方法)對機(jī)械臂運(yùn)動路徑避障效果進(jìn)行測試。

在機(jī)械臂路徑規(guī)劃過程中,路徑規(guī)劃效果優(yōu)劣、規(guī)劃時間的長短以及規(guī)劃路徑長度的大小都會對路徑規(guī)劃方法的規(guī)劃性能帶來巨大影響。采用本文方法、文獻(xiàn)[4]方法以及文獻(xiàn)[5]方法進(jìn)行機(jī)械臂運(yùn)動路徑規(guī)劃時,針對上述3種測試指標(biāo),測試3種路徑規(guī)劃方法的規(guī)劃性能。

1)規(guī)劃效果測試。

在相同的環(huán)境下,隨機(jī)設(shè)置機(jī)器人的前進(jìn)路線,采用上述3種方法進(jìn)行路徑規(guī)劃,獲取各個時段下機(jī)械臂的關(guān)節(jié)角度以及關(guān)節(jié)角速度,將3種方法的運(yùn)動角度、關(guān)節(jié)角速度與理想關(guān)節(jié)角度、關(guān)節(jié)角速度進(jìn)行對比。依據(jù)對比結(jié)果測試3種方法的路徑規(guī)劃效果,結(jié)果如圖4、圖5所示。

圖4 不同方法路徑規(guī)劃過程中關(guān)節(jié)角變化曲線

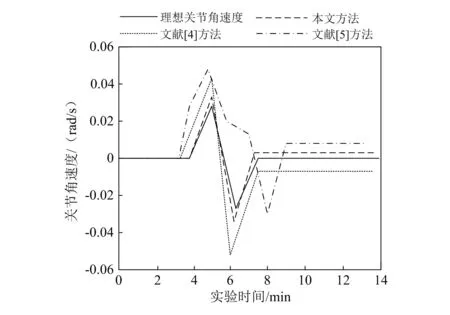
圖5 不同方法路徑規(guī)劃過程中關(guān)節(jié)角速度變化曲線

分析圖4可知,在避障路徑規(guī)劃過程中,用本文方法測試出的機(jī)械臂關(guān)節(jié)角變化情況與設(shè)定的機(jī)械臂理想關(guān)節(jié)角變化情況相接近,而用文獻(xiàn)[4]方法與文獻(xiàn)[5]方法測試出的機(jī)械臂關(guān)節(jié)角變換曲線與理想關(guān)節(jié)角變化曲線相差較大。分析圖5可知,在進(jìn)行路徑規(guī)劃時,用本文方法測試出的機(jī)械臂關(guān)節(jié)角速度測試結(jié)果與設(shè)定的機(jī)械臂理想關(guān)節(jié)角速度相近,文獻(xiàn)[4]方法與文獻(xiàn)[5]方法測試結(jié)果則不夠理想。由此可知,本文方法在進(jìn)行機(jī)械臂路徑規(guī)劃時的規(guī)劃效果好。

2)規(guī)劃路徑長度測試。

機(jī)械臂在進(jìn)行路徑規(guī)劃時,規(guī)劃路徑的長短能夠直觀反映規(guī)劃性能的好壞。規(guī)劃路徑越長,說明規(guī)劃性能越差,反之則越好。采用本文方法、文獻(xiàn)[4]方法以及文獻(xiàn)[5]方法進(jìn)行機(jī)械臂運(yùn)動路徑規(guī)劃時,對3種規(guī)劃方法規(guī)劃出的路徑長度進(jìn)行測試,測試結(jié)果如圖6所示。

圖6 不同規(guī)劃方法的路徑規(guī)劃長度測試結(jié)果

分析圖6可知,隨著測試次數(shù)的增加,規(guī)劃出的路徑長度也隨之增大。本文方法規(guī)劃出的機(jī)械臂避障路徑長度遠(yuǎn)小于文獻(xiàn)[4]方法與文獻(xiàn)[5]方法所規(guī)劃的路徑長度。這主要是因為本文方法在進(jìn)行路徑規(guī)劃前,通過拉格朗日函數(shù)對機(jī)械臂進(jìn)行了具體的動態(tài)學(xué)分析,所以在用本文方法規(guī)劃避障路徑時,規(guī)劃的路徑較短。

3)規(guī)劃耗時測試。

在進(jìn)行路徑規(guī)劃過程中,規(guī)劃時間直接影響路徑規(guī)劃方法的規(guī)劃性能。采用本文方法、文獻(xiàn)[4]方法以及文獻(xiàn)[5]方法進(jìn)行機(jī)械臂運(yùn)動路徑規(guī)劃時,對3種方法的規(guī)劃時間進(jìn)行測試,測試結(jié)果如圖7所示。

圖7 不同路徑規(guī)劃方法的規(guī)劃時間測試結(jié)果

分析圖7可知,測試次數(shù)與路徑規(guī)劃時間呈正相關(guān)。本文方法的路徑規(guī)劃時間短于文獻(xiàn)[4]方法與文獻(xiàn)[5]方法路徑規(guī)劃時間。具體而言,本文方法在路徑規(guī)劃測試中,相較于文獻(xiàn)[4]的方法和文獻(xiàn)[5]的方法,路徑規(guī)劃時間短。綜上所述,本文方法在路徑規(guī)劃過程中,規(guī)劃效果好、路徑短、規(guī)劃用時少,證明本文方法的規(guī)劃性能更優(yōu)。

4 結(jié)束語

本文提出的基于模糊變結(jié)構(gòu)補(bǔ)償?shù)臋C(jī)械臂運(yùn)動路徑避障規(guī)劃算法,能夠?qū)C(jī)械臂力矩進(jìn)行補(bǔ)償控制,并通過Q-learning算法計算最佳移動策略,實現(xiàn)機(jī)械臂的避障路徑規(guī)劃。與傳統(tǒng)路徑規(guī)劃方法相比,用本文方法進(jìn)行路徑規(guī)劃用時更短,證明其理論和應(yīng)用價值都很高,為機(jī)械臂路徑規(guī)劃提供了新的思路和方法。在未來的研究中將探索如何在復(fù)雜環(huán)境下實現(xiàn)更精確的機(jī)械臂避障路徑規(guī)劃。同時,優(yōu)化算法的計算效率和使算法適應(yīng)不同的機(jī)械臂結(jié)構(gòu)和任務(wù)需求也是未來研究的主要方向。通過這些深入研究,機(jī)械臂路徑規(guī)劃的性能和應(yīng)用領(lǐng)域?qū)⒌玫讲粩喔倪M(jìn)和拓展。