聲-地震耦合探測中亥姆霍茲共振聲通道的設(shè)計分析

徐丹萍,朱鑫權(quán),張 煥,王 馳

(上海大學(xué)機電工程與自動化學(xué)院,上海 200444)

聲波發(fā)射至地表時,會產(chǎn)生耦合作用。淺層地表的土壤顆粒之間存在著細小的縫隙,當(dāng)聲波發(fā)射至空氣和土壤的分界面時,仍存在小部分聲波能量通過振動縫隙中空氣產(chǎn)生與土壤顆粒的黏滯摩擦和動量作用而耦合至地下,引發(fā)地表下瑞利面波、橫波和縱波等地震波,產(chǎn)生聲-地震耦合現(xiàn)象[1]。當(dāng)?shù)乇頊\層埋藏有較大聲順的掩埋物時,掩埋物等效的彈簧會與上層的覆土組成一個“質(zhì)量-彈簧”諧振系統(tǒng)[2],在地震波的激勵下,此系統(tǒng)上方地表的振動狀態(tài)對比大地背景會發(fā)生明顯的變化[3]。長期以來,基于音箱的高功率低頻聲波發(fā)射模塊,一直是聲-地震耦合探測技術(shù)的主要聲源系統(tǒng)模塊,能夠較好地應(yīng)用在聲-地震耦合探測中并收集到能分析掩埋物特征信息較明顯的地表振動信號[4]。但音箱發(fā)射低頻大聲壓聲波的彌散性,使得聲波能量的利用效率很低。

亥姆霍茲(Helmholtz)共鳴器能夠大幅度提高音箱聲波能量的利用效率,而且配合聲通道腔體的約束作用,能夠有效抑制非前向低頻聲波的輻射。本文基于亥姆霍茲共振原理理論設(shè)計一種聲通道結(jié)構(gòu),將其與音箱結(jié)合進行遠距離高功率低頻聲波發(fā)射,并建立了電磁-機械-聲學(xué)三物理場耦合仿真模型,經(jīng)過實驗驗證,為后期優(yōu)化聲通道結(jié)構(gòu)與尺寸提供理論和技術(shù)支撐。實驗測試和仿真結(jié)果表明,這種音箱與聲通道結(jié)合的聲波發(fā)射系統(tǒng),不僅大幅度提高低頻聲波的能量利用率,而且大幅度降低輸入電壓,在柔性淺埋物聲-地震耦合探測系統(tǒng)的研究方面有顯見的應(yīng)用價值。

1 亥姆霍茲共振聲通道的設(shè)計

亥姆霍茲共振是指空氣在一個腔中存在的共振現(xiàn)象[5],當(dāng)驅(qū)動其腔體內(nèi)部的空氣時,在諧振的頻段附近,可以將微小的振動轉(zhuǎn)換為強度更高的聲波從管口傳輸出去,實現(xiàn)對前向輻射聲波的增強[6]和聲音放大功能。

如圖1(a)所示,一段兩端開口的聲導(dǎo)管作用與質(zhì)量塊類似,封閉腔體作用與“空氣彈簧”類似[7]。圖1(b)中,將封閉腔體和兩端開放的聲導(dǎo)管組成一個亥姆霍茲共鳴器,當(dāng)腔體內(nèi)空氣受到聲波擾動膨脹時,聲導(dǎo)管內(nèi)空氣柱受推動向外運動,腔內(nèi)壓強降低;反之亦然。在理想狀態(tài)下,腔內(nèi)空氣的壓縮和膨脹是絕熱過程,因此可通過物態(tài)方程定量求得腔內(nèi)壓強相對于大氣壓強的變化,并繪制如圖1(c)所示的等效機械諧振系統(tǒng)。在聲波的擾動下,引入聲振系統(tǒng)中的體積速,由此可得空氣柱的運動方程:

圖1 亥姆霍茲共振系統(tǒng)

(1)

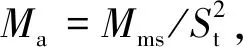
該諧振系統(tǒng)的共振頻率fR為:

(2)

式中:c0為聲音在空氣中傳播速度,L為聲導(dǎo)管長度,V為亥姆霍茲聲腔體積。

從聲導(dǎo)管末端開口向外輻射的聲波對聲源存在著反作用,需要考慮管端修正[8],共振頻率的計算公式修正后為:

(3)

式中:ΔL為聲導(dǎo)管長度L修正量,與導(dǎo)管出口的直徑正相關(guān)。

針對聲-地震耦合探測中聲激勵模塊的音箱前向輻射聲能量利用效率低的問題,本文利用亥姆霍茲共振原理效應(yīng)中聲音放大原理的聲學(xué)特性理論,設(shè)計了一種嵌套在音箱上的聲通道腔體結(jié)構(gòu),如圖2所示,其整體由前腔、后腔和聲導(dǎo)管組成,前腔和聲導(dǎo)管組成了亥姆霍茲共振結(jié)構(gòu),用于放大激勵聲波,后腔用于安置音箱,并起到防護與緊固密封的作用,本身對聲波無作用。

圖2 聲通道結(jié)構(gòu)示意圖

在聲-地震耦合探測過程中,音箱發(fā)出低頻段的掃頻探測信號時,聲波會被聲通道前腔內(nèi)的腔室導(dǎo)向引至聲導(dǎo)管內(nèi),最后通過出口發(fā)射至地面,與土壤產(chǎn)生聲-地震耦合,在這一過程中,前腔的腔室與聲導(dǎo)管之間構(gòu)成了一個諧振系統(tǒng),當(dāng)聲波的頻率恰好位于這個諧振系統(tǒng)的共振頻率附近時,會大大增加聲波的聲壓級,聲通道將原本雜亂無序的能量儲存起來,并適時釋放,起到了共振放大作用。因此在輸入相同電壓后,相比單音箱的聲源模塊,安裝聲通道的聲源模塊聲導(dǎo)管出口處能夠產(chǎn)生更大能量的聲波,從而提升系統(tǒng)對聲能量的利用效率。

在音箱箱體的封閉作用下,仿真中的發(fā)聲單元可看作是在無限大障板上的脈沖球源,且僅有半個圓球的振動對半空間聲場有貢獻,在此情況下,球源輻射聲壓p的計算公式如下所示:

(4)

式中:k為波數(shù),k=2πft/c0;ρ0為空氣密度;ρ0c0為空氣聲的特性阻抗;r為球聲源與場點之間的距離;Q0為球聲源的源強。由此可見,聲壓振幅會隨徑向距離的增大反比減小,即在球面半聲場中,離聲源越遠的地方聲音越弱。

聲壓級(SPL)的計算式為

(5)

式中:pe為聲壓的均方根值;pref為參考聲壓,pref=20 μPa。

2 電磁-機械-聲學(xué)耦合仿真分析

2.1 揚聲器單元參數(shù)

音箱整體結(jié)構(gòu)由動圈揚聲器單元和箱體構(gòu)成。揚聲器單元包括電磁域的永磁體、極片、軛鐵、音圈和機械振動域的音圈、彈撥、振膜、折邊。揚聲器單元不能直接獲得其相關(guān)材料屬性和結(jié)構(gòu)尺寸參數(shù),但可通過Klippel測量系統(tǒng)擬合出與實測阻抗近似的等效阻抗,從而獲得揚聲器單元的等效T/S參數(shù)。經(jīng)過對揚聲器進行測量(圖3),通過Klippel系統(tǒng)內(nèi)部的RL2模型[9]擬合得到圖4所示的等效阻抗曲線,并得到表1所示的等效T/S參數(shù)值,其中Re、Le為音圈的直流電阻和電感,L2、R2分別為渦流引起的等效電感和電阻,Bl為力系數(shù)。

表1 揚聲器單元的等效T/S參數(shù)值

圖3 揚聲器單元的Klippel T/S參數(shù)測試實驗

圖4 Klippel等效阻抗與實測阻抗的擬合曲線對比圖

2.2 聲學(xué)域有限元模型

在聲場的求解中,需計算音箱或聲通道出口處多個位置的聲強度,通過有限元法將研究對象的連續(xù)體劃分為有限單元,通過離散點求解的近似值逼近真實值,在合理的網(wǎng)格布置下,所求聲壓具有較高的準(zhǔn)確性和可靠性,能夠較好地用于音箱和聲通道復(fù)雜聲學(xué)邊界的求解。對音箱箱體進行測量通過三維建模可得音箱箱體結(jié)構(gòu)模型,根據(jù)音箱的結(jié)構(gòu)尺寸和聲通道腔體的聲學(xué)特性設(shè)計聲通道的結(jié)構(gòu)和尺寸,音箱和加裝聲通道音箱的聲學(xué)域有限元仿真模型分別如圖5(a)和圖5(b)所示。

圖5 聲學(xué)域有限元模型

2.3 建立耦合仿真模型

當(dāng)處于磁場中的音圈接收到交變的音頻電流時,音圈會相應(yīng)地產(chǎn)生交變的電磁力。在機械域中,音圈和振膜組成等效質(zhì)量塊,折環(huán)和彈撥組成等效彈簧,整體構(gòu)成振動系統(tǒng)。揚聲器單元工作時,電磁域中產(chǎn)生的電磁力推動機械域中音圈振動,音圈帶動整個振動系統(tǒng)振動,在磁場中切割磁感線產(chǎn)生反電動勢,由此產(chǎn)生電磁域與機械域耦合作用;另一方面,音圈帶動的振膜在振動過程中往復(fù)推動空氣并引發(fā)空氣的疏密變換,從而傳遞聲壓,空氣的疏密變換也在振膜上產(chǎn)生反作用力,由此產(chǎn)生機械域與聲學(xué)域耦合作用。考慮上述耦合作用,可得如下耦合方程:

(6)

(7)

式中:i為電路中電流,ω為電壓輸入角頻率,V0為輸入電壓,Vback為反電動勢,v為振膜振動速度,Fmag為電磁力,FD為振膜壓力。

結(jié)合測試獲得的揚聲器單元等效參數(shù)、聲場的有限元模型及電磁、機械、聲學(xué)的耦合作用,可建立如圖6所示的電磁-機械-聲學(xué)的三場耦合仿真模型,圖中u0為聲波的體積速度,SD為振膜的等效面積,P為振膜上的聲壓,采用等效電路法模擬揚聲器單元的電磁域,采用集總參數(shù)法模擬揚聲器單元的機械域,采用有限元法計算不同邊界條件下的聲學(xué)特性。

圖6 電磁-機械-聲學(xué)耦合仿真模型

3 仿真模型檢驗與分析

3.1 單音箱耦合仿真與實驗驗證

在前期的研究工作中發(fā)現(xiàn),聲-地震耦合探測中塑殼地雷與土壤所組成的諧振系統(tǒng)的共振頻率在200 Hz以下,并通過實驗驗證[10],本文主要研究塑殼地雷的聲-地震耦合探測,因此仿真模型的準(zhǔn)確性驗證頻段為20～500 Hz,其中20 Hz是實驗音箱所能發(fā)射的最低頻率。音箱的額定電壓10.1 V為仿真與實驗測試的輸入電壓。

在仿真模型中輸入電壓為10.1 V,輸入信號為20～500 Hz的1/24倍頻程掃頻信號,可得如圖7(a)所示結(jié)果,提取距離音箱聲出口0.5 m處的聲壓級值,其仿真結(jié)果如圖8所示。在圖7(b)所示的全消無響室中,于音箱聲出口處0.5 m處放置一麥克風(fēng)用來采集音頻數(shù)據(jù),輸入電壓為10.1 V,輸入信號為20～500 Hz的1/24倍頻程掃頻信號,測試結(jié)果如圖8所示。由圖8可知,仿真計算與實測結(jié)果的趨勢基本擬合,且頻段涵蓋了塑性地雷探測中所需的掃頻段。因此圖6所示的仿真模型是準(zhǔn)確的,可以用于預(yù)測音箱在不同尺寸組合的聲通道腔體作用下的聲場特性。

圖7 單音箱耦合仿真模型仿真與驗證

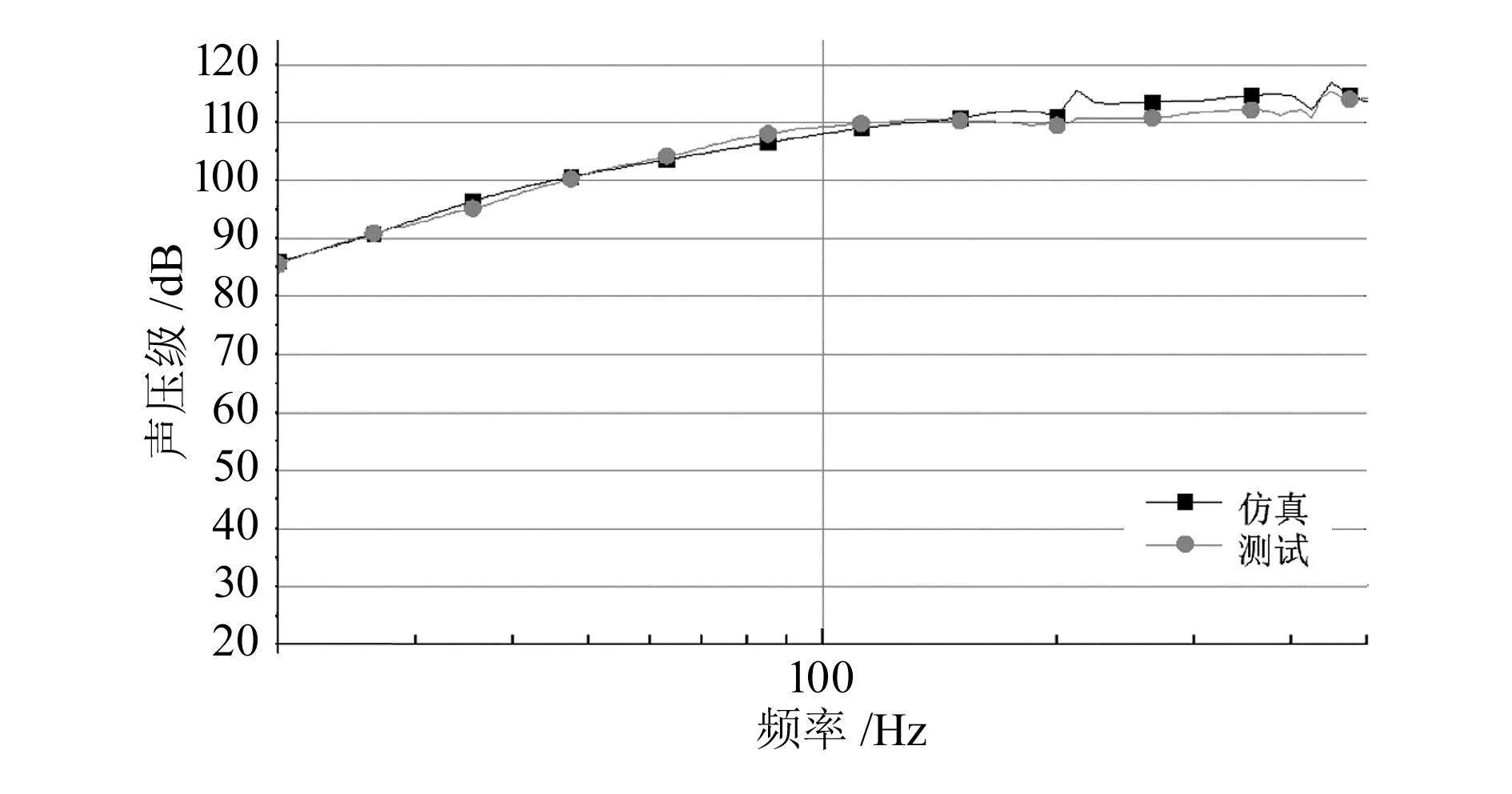
圖8 單音箱仿真計算與實測結(jié)果對比曲線

3.2 聲通道音箱模型仿真分析

在實際安裝中,聲通道存在一些尺寸的限制,例如音箱與地面之間需要垂直方向預(yù)留0.5 m,用來布置加速度計、激光自混合干涉儀和激光散斑等光學(xué)檢測儀器,因此聲導(dǎo)管的長度和前腔高度的總和需要在控制在500 mm內(nèi),如圖9所示,且根據(jù)式(3)可知,共振頻率的理論值與前腔體積、導(dǎo)管長度和導(dǎo)管直徑相關(guān),根據(jù)探測的實際限制條件和音箱結(jié)構(gòu)尺寸,設(shè)計前腔高度 40 mm、導(dǎo)聲管長度170 mm、直徑230 mm的結(jié)構(gòu)。按照聲-地震耦合探測要求,需計算發(fā)聲中心距地面500 mm直徑圓的平均聲壓級,如圖9所示。

圖9 聲壓級的定量評價標(biāo)準(zhǔn)

3.1節(jié)驗證了音箱的電磁-機械-聲學(xué)耦合仿真模型的可行性,利用同樣的仿真原理,加裝聲通道音箱的模型在輸入電壓10.1 V后仿真計算所得的聲壓級曲線與音箱仿真的聲壓級比較,如圖10所示,聲通道結(jié)構(gòu)能夠在聲-地震耦合探測頻段增強聲壓級5 dB,獲得跟音箱10.1 V輸入情況下近似的聲壓級,加裝聲通道的音箱模型的輸入電壓降低為5.3 V。

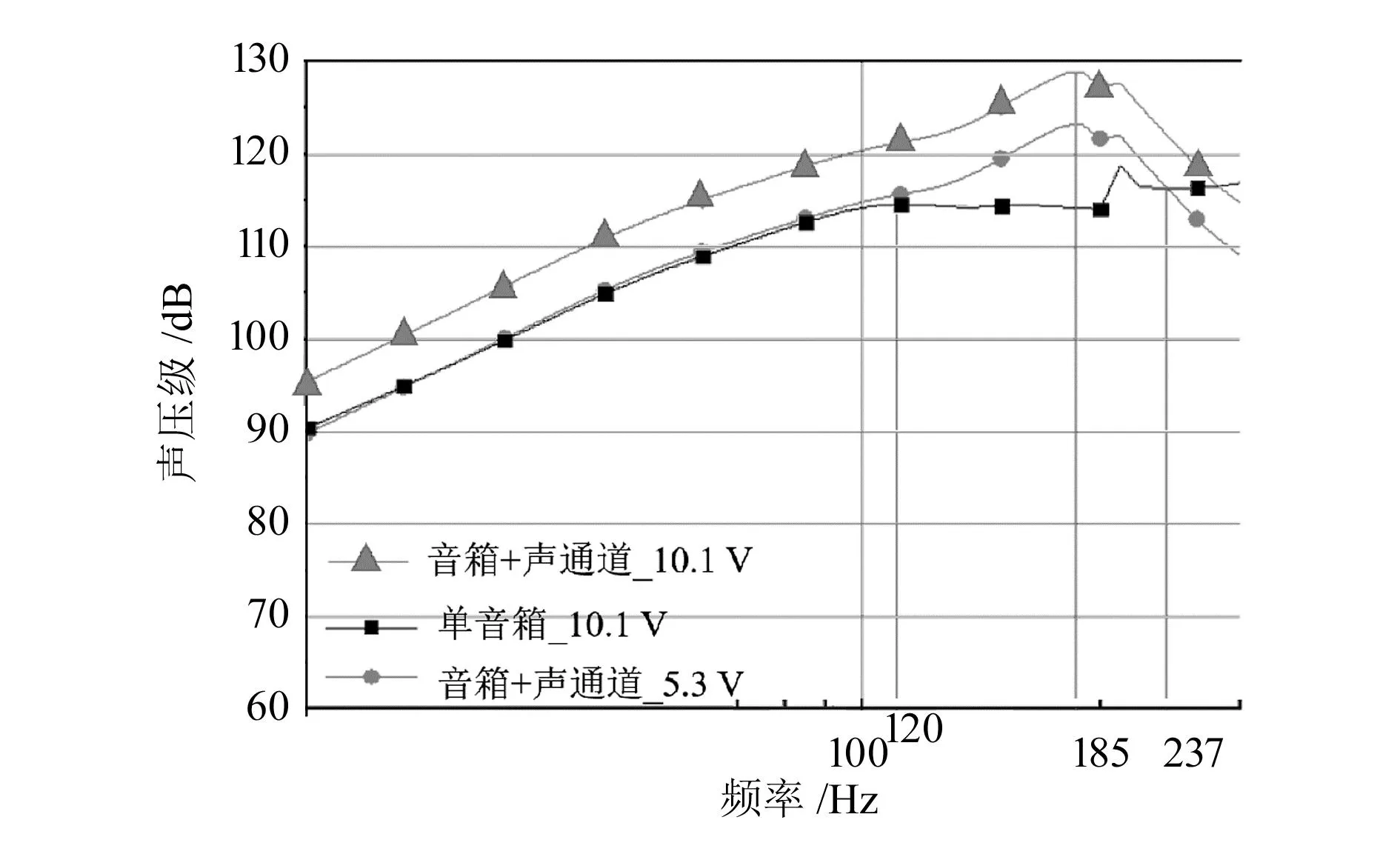
圖10 單音箱與加裝聲通道后的聲壓級仿真對比

4 結(jié)束語

本文在分析亥姆霍茲共振原理的基礎(chǔ)上,設(shè)計了一種應(yīng)用于探雷聲激勵揚聲器的聲通道結(jié)構(gòu),建立了音箱的電磁-機械-聲學(xué)三物理場耦合仿真模型,并對其進行了模型檢驗,在此基礎(chǔ)上對加聲通道的音箱模型進行仿真分析。實測結(jié)果證明,聲通道音箱結(jié)構(gòu)模型的建立和仿真分析,為下一步聲通道結(jié)構(gòu)的優(yōu)化及改進探測系統(tǒng)、開展聲-地震耦合與探測實驗、驗證聲通道在提高聲-地震耦合效果方面的有效性提供了可行性。