重構諧波平衡法及其求解復雜非線性問題應用1)

代洪華 王其偲 嚴子樸 岳曉奎

(西北工業大學航天學院,西安 710072)

(航天飛行動力學技術國家級重點實驗室,西安 710072)

引言

工程中多數動力學問題,其數學模型都是非線性的,線性系統只是在一定假設及限制條件下對非線性系統的理想化近似[1].隨著控制科學與航空宇航任務日益復雜,強非線性的影響越發不容忽視.諧波平衡法(harmonic balance method,HB)在求解非線性系統周期解中應用廣泛,但作為一種半解析半數值方法,隨著系統自由度、方法階數的增加,公式推導工作將變得困難[2].借助計算機數學軟件可輔助推導工作,但對計算效率及性能的提升作用仍然有限.采用7 階HB 法推導立方非線性項,Mathematica代碼長達1321 行.Hall 等[3]提出了高維諧波平衡法(high-dimensional harmonic balance,HDHB),通過“頻域非線性量的時域近似計算”來簡化公式推導,但是,由于引入近似關系導致非物理假解問題[4-5].Dai 等[6]發現了頻域和時域非線性項之間的條件等價恒等式,基于此,首創了重構諧波平衡法(reconstruction harmonic balance,RHB)實現超高階(N＞ 100)高精計算,并給出時域配點計算的最優采樣定理,從理論上消除非物理解.

HB 類方法(HB 法及其改進方法)不僅用于計算簡單非線性系統(杜芬、范德波方程等),還發展到航空航天、深空探測等前沿領域.哈爾濱工業大學陳毅等[7]使用諧波平衡?交變頻域/時域法(HBalternating frequency-time,HB-AFT)用于求解航空發動機中雙轉子?軸承?機匣系統動力學方程.中山大學陳衍茂等[8]使用增量諧波平衡法對帶機外掛載的二元機翼進行動力學特性研究.RHB 法也被作為三體軌道的設計依據,計算結果符合鵲橋中繼衛星實際飛行數據[6].

但是該方法仍面臨著兩個問題: (1)諧波平衡法的本質依賴于非線性項的傅里葉級數展開,因此,受限于多項式型非線性系統求解,對于非多項式型復雜非線性問題,諧波平衡法難以適用;(2)已有諧波平衡類方法建立在單基頻的假設上進行級數展開,由于擬周期響應存在多基頻的特征,因此已有方法難以直接求解高精度擬周期解.

針對非多項式型非線性系統的求解問題,目前有兩類處理方法,分別為直接法和間接法.直接法包括HB-Taylor 法[9]與HB-AFT 法[10-11].HB-Taylor 法通過泰勒級數展開將非線性函數用有限階近似多項式描述;HB-AFT 法通過對非線性項的時域值采樣以離散原問題.由于直接法對原系統進行了近似,導致求解精度低,且計算性能分別受制于高階級數描述和過采樣等問題.Cochelin 等[12]提出的諧波平衡?重鑄法(HB-recast)是一種間接方法,通過重鑄(recast)技術,成功將復雜非線性微分動力學系統無損變換為多項式型微分代數方程,然后用HB 法加以求解[13-14].但是,受限于HB 法的高階計算(使用重鑄法會增加系統的維度,進一步增加了高階計算的難度)與原重鑄形式的二次型限制(原方法要求新系統中非線性至多為二次多項式),至今難以對復雜非線性系統周期響應進行高效高精求解.

第2 個難題是擬周期響應求解問題.擬周期響應大量出現在非線性動力學系統中[15-17],其頻率響應由多個不可約基頻及其線性組合描述[18].由于傳統HB 類方法基于單個基頻進行近似解逼近,不能簡單通過基頻及其整數倍頻率分量對擬周期響應描述,Chua 等[19]提出了結合廣義傅里葉級數的改進多頻HB 法,實現擬周期響應的準確求解.然而,使用多頻HB 類方法對強非線性項進行頻域內高階描述時,計算效率嚴重受限于高維傅里葉分析(頻域分量由多重積分[20]、求和[21]計算得到).Liu 等[22]使用多頻HDHB 法求解受迫范德波振子的穩態響應,避免非線性項諧波系數的直接表示以提高求解效率,但是多頻HDHB 法的精度受到非物理解的破壞[23].總之,當前關于HB 類方法的研究已拓寬到對擬周期響應求解領域,然而由于多基頻計算中的高階頻域描述困難,對此類復雜響應的高性能求解尚待解決.

針對上述問題,本文提出了RHB 法與重鑄法、多頻諧波平衡計算相結合的兩種方法: (1) RHB-重鑄法;(2)重構多諧波平衡法(reconstruction multiple harmonic balance,RMHB).一方面RHB-重鑄法通過將一般非線性等價轉化為多項式型非線性系統,再采用RHB 法以確定時域最優采樣點數,實現對復雜非線性動力學系統的高階高精求解,仿真誤差達計算機精度.另一方面,RMHB 法通過篩選和補充多個基頻,借鑒RHB 法的時域等價重構思想,完善了學術界在使用多頻HB 類方法求解擬周期響應時消除混淆假解的理論研究.

1 諧波平衡法及重構諧波平衡法

1.1 諧波平衡法

對非線性動力學系統

HB 法用有限階傅里葉級數來構造近似解及其導數

其中N是HB 法的階數.x0,x1,···,x2n為未知傅里葉系數,也被稱為頻域變量,將頻域變量組成待求解向量=[x0x1···x2n]T.假設多項式函數f(x)=x?,忽略由非線性項而出現的高次諧波,只需展開前N次的傅里葉分量

其中各次分量r0,r1,···,r2n為

其中n=1,2,···,N;θ=ωt.將表示非線性函數的傅里葉分量記為,是待求解向量x? 的非線性函數.

將式(2)～式(4)代入微分方程(1),令常數項及前n次諧波 cosnωt和 sinnωt(n=1,2,···,N) 系數配平,得到非線性代數方程組

其中,分塊矩陣A為

由三角函數的求導關系得到.

非線性項的近似表示(4)中,符號運算的復雜度會隨算法階次的提高呈指數增長[6].當HB 法的階數超過20,即便有計算機數學軟件的輔助,非線性項的推導整理工作量仍難以接受.

1.2 高維諧波平衡法

為簡化HB 法的符號運算量,Hall 等[3]使用時域值替代頻域分量,即將N階HB 法中的傅里葉系數作用轉換矩陣EHDHB,建立與一個周期 2N+1 個等距配點上時域量間的聯系,定義

將式(7)代入HB 法代數方程組(6)得到HDHB法求解微分方程(1)對應的代數方程組

HDHB 法顯著提高計算效率,并被認為是HB法的一種改進,在計算流體力學領域得到應用[2,24].但該算法求解強非線性動力學問題時產生非物理解(也稱假解),嚴重影響求解精度.如圖1 所示,HDHB 法計算結果雖然是方程組(8)的數學解(使求解算法收斂),但已偏離了真實的物理響應.

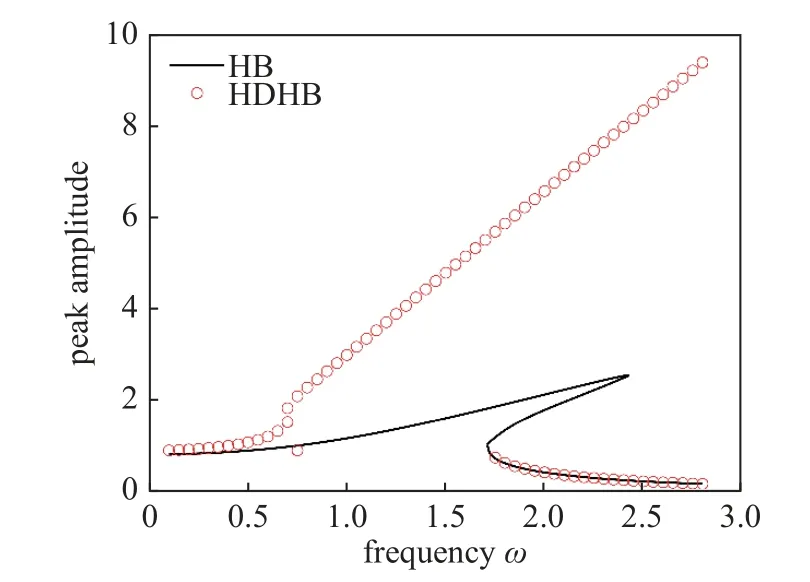
圖1 HB 法和HDHB 法計算杜芬方程對比(N=2)Fig.1 Comparison of the Duffing equation computed by the HB and HDHB methods (N=2)

Liu 等[4]指出,假解現象產生于對非線性項近似的過程中,存在高階諧波對低次的混淆(污染).以立方項非線性x3為例,二階HB 法中() 表達式

HDHB 法計算中,非線性項的頻域分量(9)中不僅包含了原HB 法中的所有項,還包括附加雜項,這些雜項的混入導致求解中出現非物理解

1.3 重構諧波平衡法

Dai 等[25]證明,HDHB 法與時域配點法等價,時域配點法通過使用時域配點上函數值對微分方程進行離散,從而聯立代數方程組

其中配點矩陣

混淆是造成計算出現非物理解的原因.至于高次諧波在時域配點計算中影響低次諧波的機理,則遵循“混淆規則”[25].

混淆規則:假設 α ∈[0,π] 被以h為間隔均分為離散時間點,那么配點法中可區分的最大諧波次數n∈[?L,L],其中L=π/h,L為“極限波次”.高次諧波n(|n|＞L) 被誤認為是相應低次諧波na

其中na∈[?L,L],m是整數.

混淆規則指出,時域配點法可區分的最大諧波次數由配點數(離散時間點的間隔)決定.增加時域配點法中的配點數量,可區分的諧波次數越高,此時方程(10)個數多于待求解變量數,配點矩陣E為列滿秩矩陣,存在Moore-Penrose 廣義逆矩陣E?

其中I2N+1為單位矩陣.在配點法方程同時作用矩陣E?,對方程組降維,得到RHB 法代數方程組

RHB 法在保證算法效率的同時,消除非物理解,從而實現對原HB 法的最佳重構.定理1 圍繞如何選擇合適的配點數,給出消除混淆確定條件[6].

定理1(條件等價性):如果配點數M,方法階數N,多項式非線性的冪次 ? 滿足

則RHB 法與HB 法等價.

為說明RHB 法消除混淆的效果.分別使用HDHB法和RHB 法計算杜芬方程,在分岔處(頻率 ω=2)進行蒙特卡洛法模擬,選取104組隨機初值(各頻域分量在區間[?2,2]中選取),得到如表1 所示的統計結果.統計結果表明,HDHB 法計算產生58 組解,其中55 組都是非物理解;而RHB 法只計算得到3 個具有物理含義的解[6].

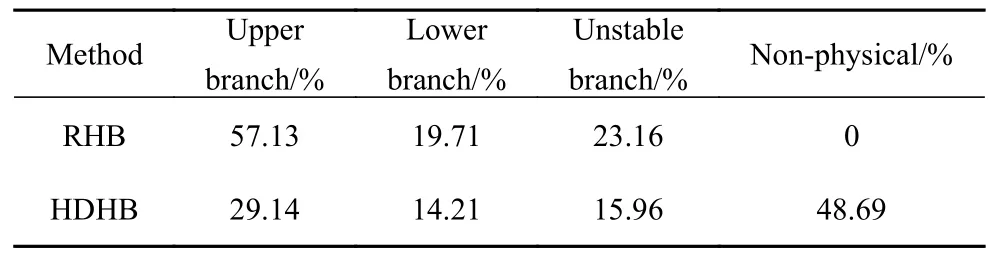
表1 RHB 法與HDHB 法在分岔處的解分布Table 1 Statistical distribution of solution by the RHB and the HDHB method at bifurcation point

此外,HB-AFT 法與HDHB 法計算流程一致,但HB-AFT 法的原理是,選用配點數 2?N+1 來消除混淆[11],但過采樣會占用計算機資源,在實際計算時會導致更大的CPU 和RAM 計算負擔[2].RHB 法基于時域配點法的統一框架,根據配點數的差異將所有HB 類方法(HDHB 法、HB-AFT 法等)建立起聯系.

2 重構諧波平衡法改進策略

2.1 微分方程重鑄技術

針對非多項式型非線性系統的HB 法求解,Cochelin等[12]提出將原系統改寫為二次型系統

其中未知向量z包含微分方程的原始變量x及一些新的變量(引入的新變量用以改寫方程).c是關于未知量z的常數向量;l是關于z的線性向量值運算符;q則是二次向量值運算符.

因為對任意x?次非線性,RHB 法都能實現高效計算,改寫后方程可以是更高次多項式,將式(13)進一步寫成適配于RHB 法的微分方程重鑄形式

其中n可以是關于變量z的任意 ? 次多項式函數.重鑄格式(14)涵蓋多類型非多項式型非線性問題,下面將分類加以介紹.

(1)微分項耦合型

通過將方程重鑄為標準形式(14),得到

原方程轉化為典型的非線性度 ?=3 的動力學系統.得出結論: 導數項的耦合不影響非線性度計入,在實際HB 計算中,任意階導數只計入一個非線性度.

(2)有理分式型

以Rayleigh-Plesset 方程為例

式中,A,B,C,D均為常系數.將方程兩端同除以R,并運用倒數關系,令v=,x=1/R得到[6,12]

處理有理分式型非線性項,通過額外增加方程Rx=1,將方程改寫為非線性度 ?=4 的多項式型非線性系統.

(3)根式型

相對論諧振子方程(17)中非線性項為根式

對任意形如 αq/p的根式,令 βp=α,使原根式型非線性轉化得到多項式型: αq/p=(βp)q/p=βq.

(4)初等超越函數

對初等超越函數的處理,需要導數信息來實現對原微分方程的重鑄.以非線性單擺方程為例

由于三角函數是超越函數,不能通過簡單的代數關系式改寫轉化為多項式型.首先額外引入兩個變量s,c來分別表示s(t)=sinθ(t),c(t)=cosθ(t).利用三角函數的導數性質

建立補充方程,從而實現對微分方程組的重鑄[13]

初等超越函數非線性的重鑄,以導數關系作為方程組改寫的依據(部分需要用到有理分式、根式型非線性重鑄技巧).附錄表格中羅列了幾類常見初等超越函數改寫思路與重鑄形式,可供參考.

總之,本文主要針對非線性項為連續函數情形(包括微分項耦合、有理分式型、根式型以及初等超越函數4 類),重鑄技術通過變量替換、利用特殊函數的導數關系(見附表1)等關鍵步驟將一般連續函數非線性項改寫為更利于重構諧波平衡法求解的多項式形式(14).

2.2 多諧波平衡計算

“補頻”(supplemental frequency)思想[17]是在原來單頻假設的基礎上,補充多個與響應相關的頻率.假設考慮兩個基頻,將假設函數改寫為

參數m和n滿足不等式

其中p代表二維傅里葉級數的截斷[19-20],類似于RHB法中階數N.

以RHB 法理論為基礎,提出的RMHB 法利用時域信息,將動力學問題(1)轉化為非線性代數方程(11)求解.多基頻計算中,配點矩陣E以及轉換矩陣E?形式,記cm,n=cos(mω1+nω2)t,sm,n=sin(mω1+nω2)t.在RMHB 法計算中,存在選取合適的采樣周期和時域配點數用以消除混淆的結論[23].

定理2(多頻計算中條件等價性):假設多項式非線性的冪次 ? 的非線性系統響應中包含兩個基頻,基頻之比 ω1/ω2為有理數.則RMHB 法消除混淆需滿足采樣時間T=2π/GCD(ω1,ω2),配點數

其中 GCD 為兩數最大公因數.

3 數值仿真結果

3.1 相對論諧振子

作為物理學中經典問題,有必要對諧振子模型進行完整而嚴格的相對論處理[26].考慮一個靜質量為m的質點在一維諧振力F=?的作用下做相對論運動.其中k為彈性常數,為位移量.結合牛頓運動運動學方程以及動量定理,可以推導得到相對論振子方程[27-28]

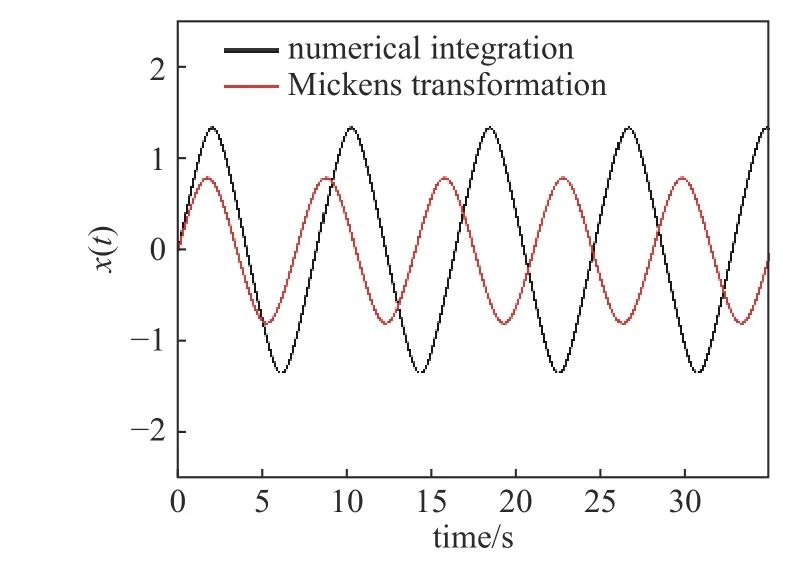
圖2 Mickens 變換解與真實物理解對比Fig.2 Comparison of Mickens transformation result and real physical solution

RHB-重鑄法按照根式型非線性重鑄原則,將相對論諧振子改寫為方程(18),再使用高階RHB 法求解.結合表2 和圖3,RHB-重鑄法可對高速運動的諧振子(β=0.85)直接進行高階計算.55 階RHB-重鑄法能將計算誤差控制在 10?12量級(以數值積分為參照,全文采用MATLAB 內置函數ode15 s,相對精度容差 10?13,絕對誤差容限10?20),總計算耗時在1 s 內.

表2 各階RHB-重鑄法求解相對論諧振子Table 2 Solving relativistic harmonic oscillator by the RHBrecast method with different orders

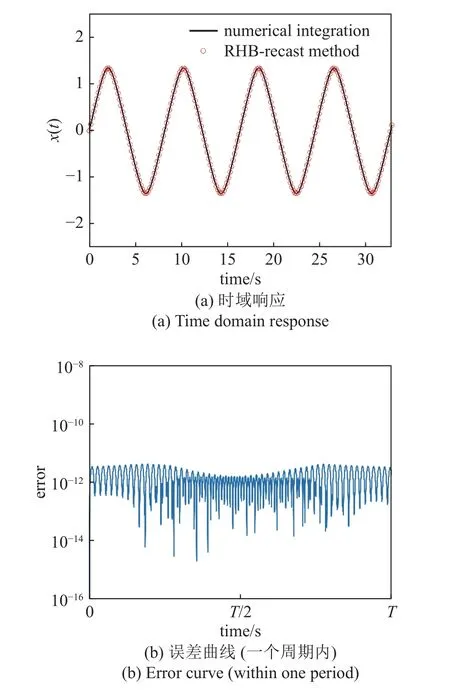
圖3 55 階RHB-重鑄法求解相對論諧振子的計算結果Fig.3 The computing result of the RHB-recast method (N=55) for solving relativistic harmonic oscillator

除通過方法階數對求解精度的提高,還能通過兩種方式實現對計算性能的改善.

(1) 非線性代數方程組求解算法

非線性代數方程(11)求解算法能提高HB 類方法計算性能,Zheng 等[31]結合Tikhonov 正則化求解,黃建亮等[32]引入狗腿法思想結合回溯線搜索算法求解,Thomas 等[33]使用Broyden 法以提高HB 法計算性能.本文根據算例來說明L-M (Levenberg-Marquardt)法較之傳統迭代方法在求解RHB 方程組時體現出的優勢.圖4 展示當 β=0.85,頻域量初值估計x2=1,u0=0.7,使用兩種不同的方程組求解算法: 牛頓迭代 (Newton-Raphson)法與L-M 法得到的一個周期內誤差曲線.不同于牛頓迭代法,L-M 法迭代格式為[34]

圖4 非線性方程組求解算法對計算精度的影響(相對論諧振子)Fig.4 Influence of nonlinear equation algorithm on calculation accuracy (relativistic harmonic oscillator)

其中xk為當前迭代未知變量值,Fk為函數值,Jk為雅可比矩陣.L-M 法通過衡量每步迭代的誤差是否發散,來決定撤回迭代并將參數 λk按十倍放縮.LM 法在求解非線性方程組時顯示出更高的計算精度,同比牛頓迭代法,精度提高了 104以上.

(2) 合理選擇代數方程

相對論諧振子(17)為保守系統,振動頻率 ω 是狀態變量[35].使用RHB-重構法對n自由度保守系統求解時,共需考慮n(2N+1)+1 個變量,需額外增加一個代數方程使RHB 方程組適定.本文以初值約束來探討方程對計算性能的影響.圖5 為采用55 階RHB-重構法與L-M 法求解器,使用不同代數方程(約束條件)得到的誤差曲線.分別對應: 初始位移約束x(0)=0;初始速度約束(0)=β;同時考慮初始位移與速度約束.同時考慮位移與速度約束時,RHB-重構法計算精度更高.

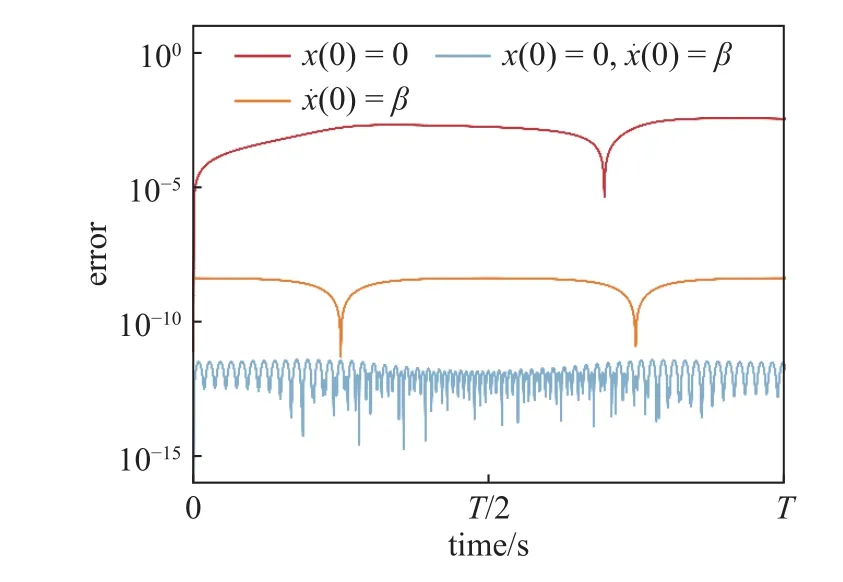
圖5 改變代數方程對計算精度影響Fig.5 Influence of changed algebraic equation on calculation accuracy

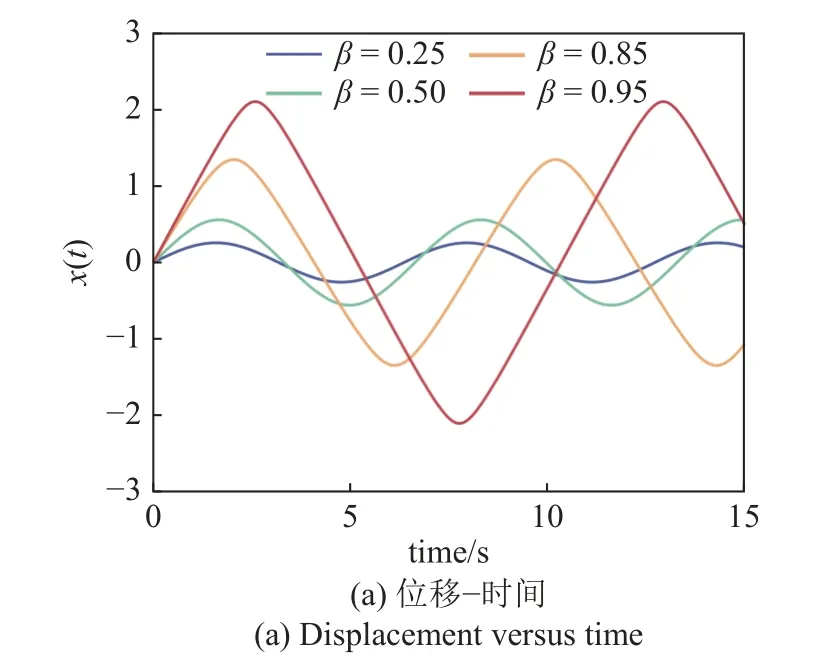
相對論諧振子在高速運動時顯示出復雜的動力學特性,需要高階(＞20 階)方法來進行分析.使用重鑄技術,將根式非線性轉化為多項式型,再使用RHB法實現快速解算,克服高階估計的限制.如圖6 所示,RHB-重鑄法適用于不同初速度條件下相對論振子的計算.

3.2 非線性單擺

非線性單擺(19)是物理學中經典問題,且時域響應具有典型的周期性.但現有HB 類方法不能做到高性能求解: HB-Taylor 法需要采用高的截斷階來保證計算精度;HB-AFT 法則需進行過采樣以抑制混淆誤差(如圖7 所示).

對非線性單擺重鑄,得到方程(20).使用25 階RHB-重鑄法求解(大角度擺動,θ(0)=1.5),初值估計x1=1.423,s1=1.065,c0=1.028,輔助L-M 法求解器,計算結果如圖8 所示,與數值積分參考解比較,誤差控制在 10?12數量級以下.

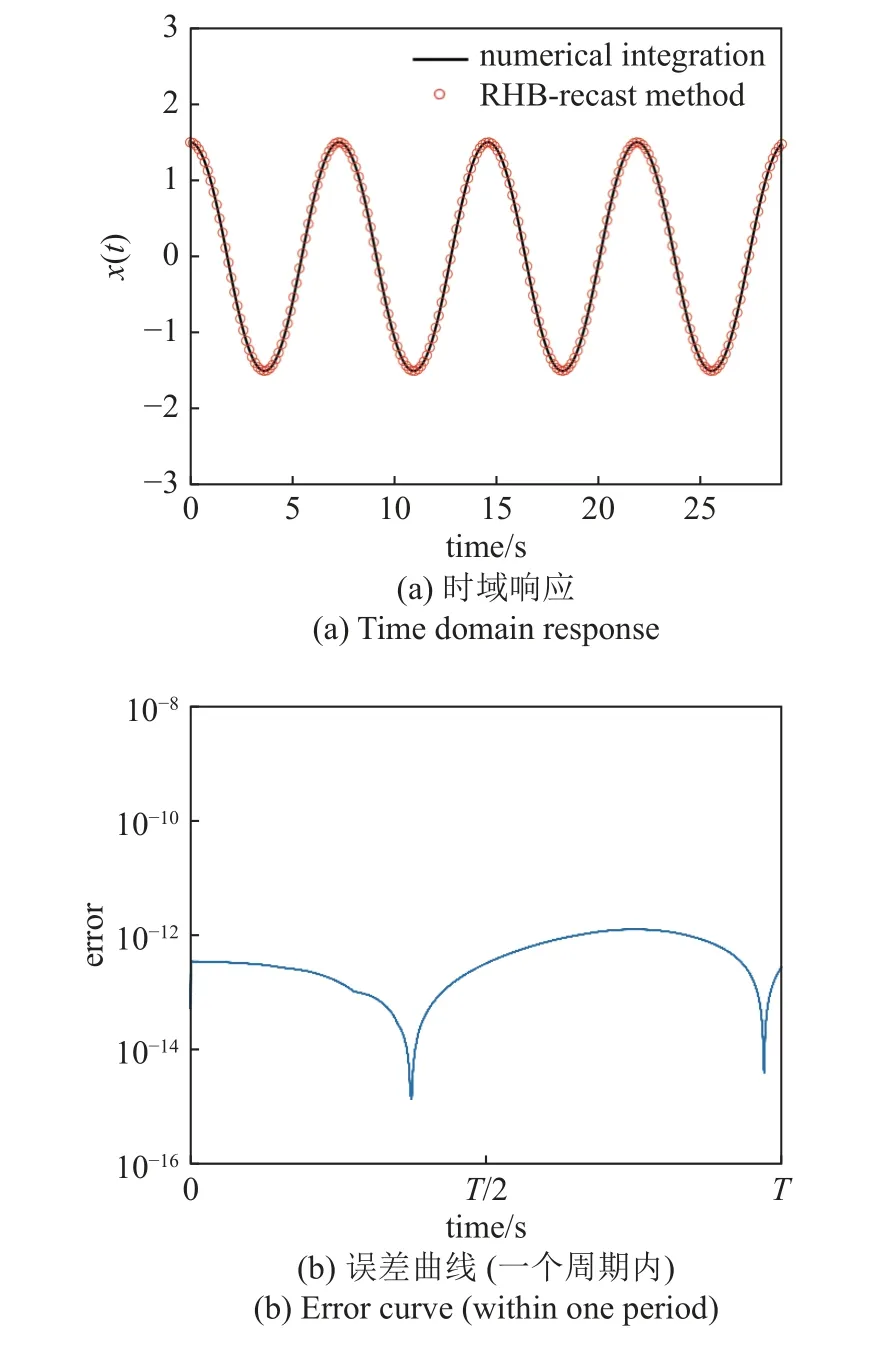
圖8 25 階RHB-重鑄法求解非線性單擺Fig.8 The computing result of the RHB-recast method (N=25) for solving nonlinear pendulum

分別采用牛頓迭代法、Tikhonov 正則法與L-M法得到圖9 計算結果.牛頓迭代法中雅可比陣奇異,求解失效;Tikhonov 法與L-M 法計算所得的誤差數量級相近,但是由于Tikhonov 法對正則參數的優化使求解更耗時[31].本例中,使用L-M 法計算RHB 法方程組僅需0.72 s,而Tikhonov 法耗時達1.17 s,L-M法較之Tikhonov 法效率提高了62.5%,達到了相近的求解精度.對比傳統方法(牛頓迭代法)與優化方法(Tikhonov 法),L-M 法都更適合于RHB 法方程組的求解.

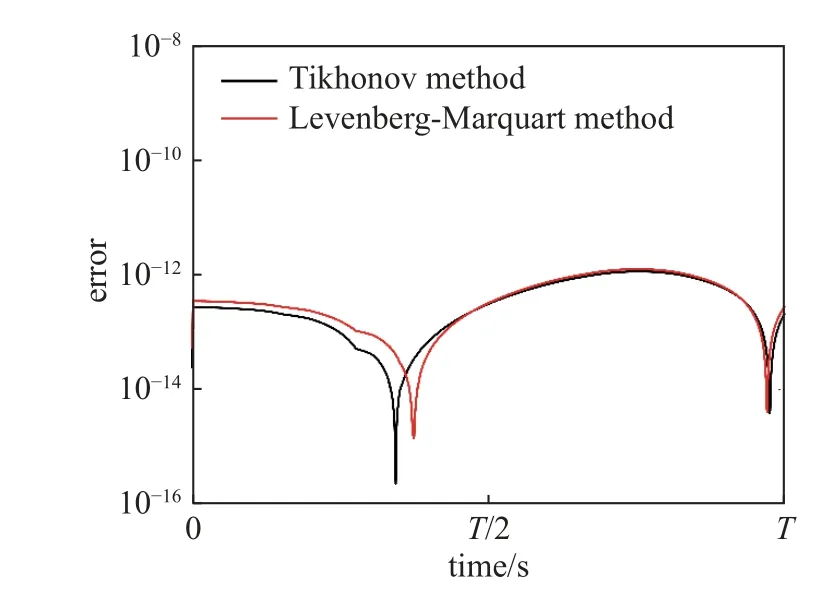
圖9 非線性方程組求解算法對計算精度的影響(非線性單擺)Fig.9 Influence of nonlinear equation algorithm on calculation accuracy (nonlinear pendulum)

非線性單擺問題是保守系統,其周期解 θ(t) 與響應頻率都依賴于初始振幅 θ(0).使用RHB 法求解重鑄方程組(20)時,本文給出3 種代數方程組合方案,以助于對比分析.

方案1: 對未知量 θ,v,s和c全諧波平衡(從常數項到N次諧波項),計 4(2N+1) 多個方程.增加初始振幅約束 θ(0)=α.

方案2: 對未知量 θ 和v全諧波平衡,計2(2N+1)多個方程.s和c從1 次諧波開始,平衡系數到N次,計 2N多個方程.增加初始振幅約束 θ (0)=α 與兩個對附加變量s,c的初值約束

方案3: 對未知量 θ 和v全諧波展開,計2(2N+1)多個方程.s和c從1 次諧波展開到N次,計 2N多個方程.增加初始速度約束v(0)=0 與兩個對附加變量s,c的初值約束式(24).

分別采用3 種方案得到的計算結果如圖10 所示.對比方案2 和方案3,方案1 的計算誤差大,主要原因是沒有對附加變量s和c的初值進行約束.方案3 同時利用了初始位移與速度信息,比方案2 計算精度更高.

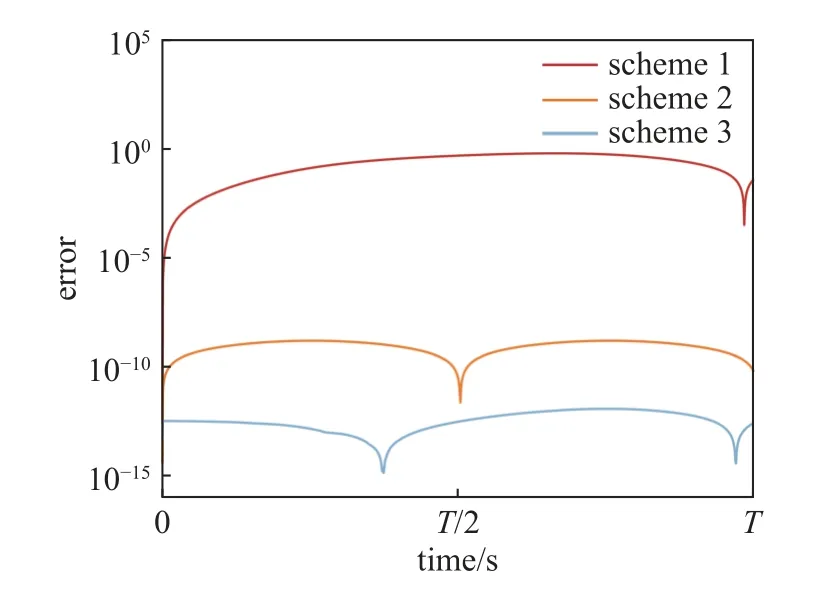
圖10 不同代數方程組合方案對計算精度影響Fig.10 Influence of different combination schemes of nonlinear algebraic equation on calculation accuracy

對比求解非線性單擺的3 種方法(HB-AFT法、RHB-Taylor 法和RHB-重鑄法)計算結果.考慮同階截斷N=25,綜合圖11 誤差曲線和表3 的計算結果,RHB-重鑄法確定最優時域配點數M=76,降低采樣成本.RHB-Taylor 法雖可采用高階截斷(15 次多項式)保證計算精度,但超越函數的級數表示降低計算效率,計算用時達1.80 s.RHB-重鑄法與HB-AFT 法計算效率相當,但將計算精度提高了兩個數量級以上.

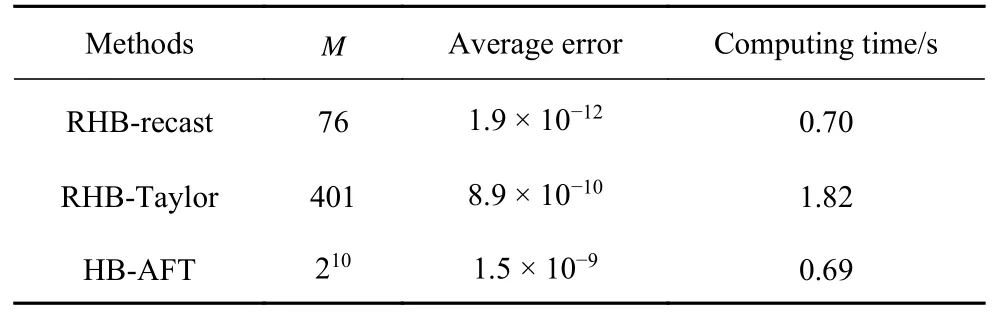
表3 3 種方法計算非線性單擺結果對比Table 3 Comparison of corresponding results of three methods for solving nonlinear pendulum

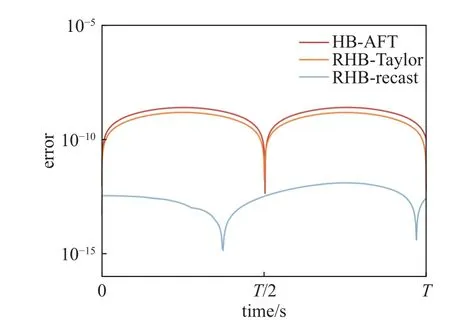
圖11 3 種方法求解非線性單擺對應誤差曲線對比Fig.11 Comparison of corresponding error curves of three methods for solving nonlinear pendulum

RHB-重鑄法適用于求解初等超越函數非線性問題.尤其是當單擺做大幅度振動時,傳統的線性化手段無法很好地捕捉動力學響應,而RHB-重鑄法則可以提供高精度解析解(圖12).

圖12 RHB-重鑄法求解非線性單擺問題: 相平面圖Fig.12 The RHB-recast method for solving nonlinear pendulum: phase plot

3.3 非線性耦合的非對稱擺

用繩將質點小球懸掛于一根固定在鐵架上的彈性桿末端,而彈性桿能在水平面與質點小球同步振動.此物理模型在許多其他二維擺系統中普遍存在,如球面擺、傅科擺等.特別地,當傅科擺由于不完美的懸掛或由于側向運動引起非線性耦合而導致不對稱,可能會導致額外的旋轉,從而掩蓋地面效應.非線性耦合的非對稱單擺微分形式可以寫作[36]

此方程中2 階導數耦合入非線性項,導致使用傳統方法進行直接求解變得棘手.以傳統的有限差分類方法(歐拉法、龍格庫塔法、MATLAB 內置ode算法等)而言,需額外計算代數方程組來輔助求解.而部分解析求解法的計算效果同樣不佳,Jia 等[36]曾采用多時間尺度法推導方程的解為

令參數 κ=0.01,初始條件x(0)=0.1,y(0)=0.2,(0)=(0)=0.

以修正Chebyshev-Picard 迭代 (modified Chebyshev-Picard iteration,MCPI)法計算結果為標準解[37-38].仿真得到如圖13 所示,解(26)不僅推導復雜,且與真實的物理解間有較大誤差.

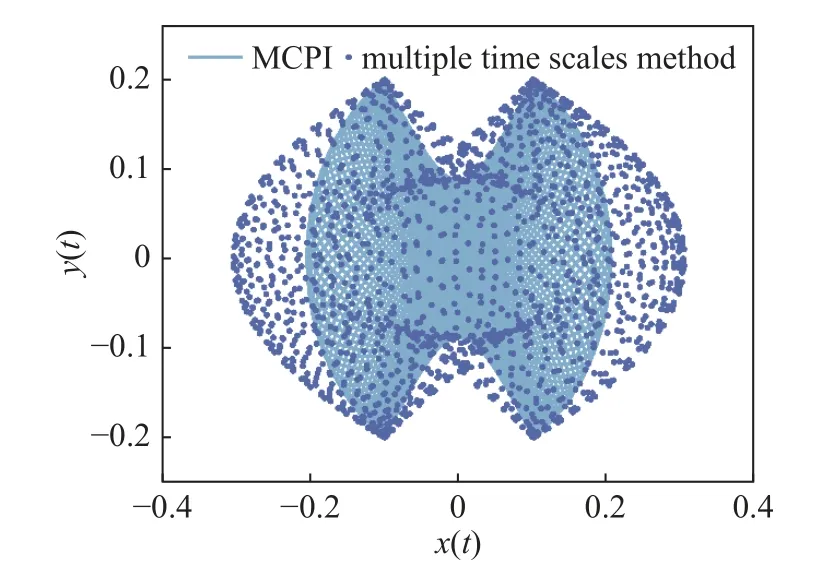
圖13 多時間尺度法與修正Chebyshev-Picard 迭代法(參考解)求解軌跡對比Fig.13 Comparison of the method of multiple scales and the MCPI method (reference solution) for solving trajectory diagram

對多時間尺度解(26)分析得知,動力學響應包含兩個基頻(所有頻率成分都是基頻的線性組合),通過快速傅里葉變換(FFT)得到: ω1=0.985 7,ω2=0.993 5.又從微分方程重鑄的角度分析非對稱擺微分方程(25),因為高階導數只算作一個非線性度,該方程是具有3 次多項式非線性的動力學系統.使用5 階RMHB 法進行計算得到圖14 所示仿真結果,計算用時8.24 s,x方向振動幅值誤差 9.21×10?3,y方向振動幅值誤差 3.90×10?7.

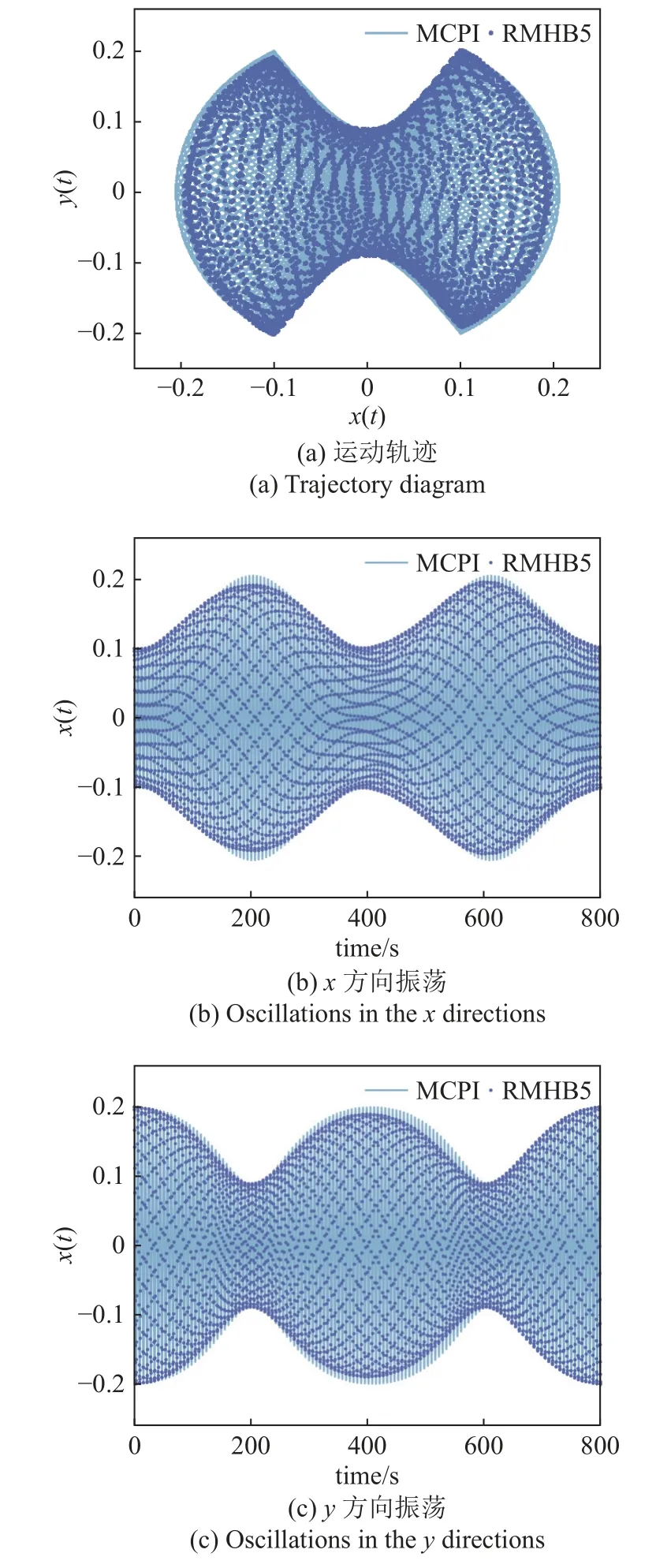
圖14 5 階RMHB 法求解非線性耦合非對稱擺Fig.14 Solving nonlinear coupling asymmetric pendulum by the RMHB5

對2 階導耦合型非線性系統,有限差分方法不能直接求解,一些解析求解方法的計算精度低.考慮兩個基頻的RMHB 法不僅保證計算效率,還能對擬周期運動進行準確的預測.

4 結論

圍繞復雜非線性動力學系統高效高精度周期解算需求,本文基于微分方程重鑄、“補頻”等思想,分別提出RHB-重鑄法與RMHB 法,主要的工作與結論總結如下.

(1)提出RHB-重鑄法,將一般非線性問題改寫為多項式型非線性方程,配合RHB 法確定消除非物理解所需的最優配點閾值,實現對非多項式型非線性動力學系統周期響應進行高階預測.數值實驗說明,對比HB-AFT 法的時域過采樣和HB-Taylor 法對非線性函數進行泰勒級數截斷兩種處理方式,RHB-重鑄法的計算精度高達 10?12,且計算時間不超過1 s,同時保證了求解的高精度與高效率.

(2)提出結合“補頻”思想的RMHB 法,在原來單頻假設的基礎上,補充多個與物理響應相關的頻率.借鑒RHB 法中時域重構等價性,給出多頻諧波平衡計算的最優配點數結論,并充分利用非線性量的時域采樣代替復雜的高維傅里葉分析,最終實現對擬周期響應的準確捕捉.

(3)通過解算相對論諧振子、非線性單擺以及非線性耦合的非對稱擺問題驗證了本文算法的有效性.針對傳統有限差分類方法求解困難的多自由度耦合系統,RHB 及本文提出的兩種方法都不受方程形式的限制.此外,在相同的系統參數設置下,合理地選擇代數方程求解器、代數約束方案,可有效提高非線性問題的求解精度.

本文提出的RHB-重鑄法與RMHB 法對復雜非線性動力學系統周期性及擬周期響應的計算效率與精度相較于現行的方法與處理方式都具有優勢.在后續的研究中,將探究RHB 法在高精周期響應求解方面的工程應用.

數據可用性聲明

支撐本研究的科學數據已在中國科學院科學數據銀行 (science data bank) ScienceDB 平臺公開發布,訪問地址為: https://cstr.cn/31253.11.sciencedb.j00140.00022 或https://doi.org/10.57760/sciencedb.j00140.00022.

附錄A

附表A1 常見初等超越函數的重鑄Table A1 Recast form of the most common elementary transcendental functions