軌道車輛垂向輪軌力時域識別對比及其機器學習修正1)

朱 濤 吳佳欣 王小瑞 肖守訥 陽光武 楊 冰

(西南交通大學軌道交通運載系統全國重點實驗室,成都 610031)

引言

軌道車輛的輪軌接觸力是評判其運行安全性與穩定性的重要依據,然而輪軌接觸力往往難以直接獲取.目前輪軌力的獲取主要有直接測量法[1-3]和間接測量法[4-6].直接測量法主要是采用測力輪對或測力鋼軌,均需要復雜的標定過程,且需要后續維護,較難以推廣使用[7].間接測量法即使用動載荷識別方法,利用測量的車輛響應,識別出精度可以接受的輪軌力值.在諸多載荷識別方法中,時域法憑借計算過程直觀,可識別的載荷類型多,可識別短樣本數據(克服了頻域法的缺點),并且還可做到實時識別等優點,獲得了廣泛的關注與應用[8-11].此外,機器學習方法由于具有非線性映射能力強等優點,被廣泛應用于復雜機械系統中.

Ronasi 等[12]提出了一種輪軌力識別的優化方法,將車輪視為二維圓盤,建立其有限元模型,通過車輪的徑向應變時間歷程來識別輪軌力,并通過加入正則化方法,提高了模型的抗噪性.Wu 等[13]采用Green 函數法建立反演模型,使用TSVD 正則化方法結合預測響應誤差最小原理,對軌道車輛輪軌力進行了識別.朱濤[14]基于動態規劃方法,結合Bellman 最優化原理建立了高速列車輪軌力識別模型,并引入正則化方法消減反問題的不適定性,獲得了較好的識別效果.郭劍峰[15]提出了一種基于數據建模的軌道車輛輪軌力識別方法,將經過預處理的實測車輛響應和輪軌力進行特征數據融合,并作為模型的輸入,采用基于多節點神經網絡的方法對輪軌力進行識別,并與其他類型的神經網絡方法進行了對比.Sun 等[16]基于數值修正的Newmark-β法,建立了一個逆向貨車動力學模型來識別輪軌接觸力,通過VAMPIRE 仿真模型對兩個軌道軌頂面和橫向不平順的情況進行了模擬,然后將模擬的貨車部件加速度輸入到逆向貨車模型中.對一系懸掛力、二系懸掛力和輪軌接觸力的預測與模擬結果進行了比較,結果趨于一致,此后,進一步將逆向貨車模型簡化為一個3 自由度的1/4 車垂直模型,以便于在線應用.孫善超等[17-18]結合最優控制理論、卡爾曼濾波方法以及輪軌蠕滑理論,建立了輪軌作用力的全息辨識模型,將輪軌作用力辨識問題轉換為最優控制策略的設計問題,并結合卡爾曼濾波技術及加速度測試值,對動載荷預測值進行正向修正,最終實現了輪軌左、右橫向力的識別.周亞波[19]基于線性卡爾曼濾波算法,對軌道車輛垂向輪軌力和橫向輪軸力進行了辨識,并驗證了在軌道隨機不平順、車輪扁疤及車輪多邊形激勵下該方法的準確性.Zhu 等[20]基于Duhamel 積分推導了一種時域動載荷識別方法,將其應用于車輛通過直線和曲線工況的輪軌力識別,并將識別結果與動力學仿真結果進行對比,結果表明該方法具有較高的識別精度.羅金屯等[21]基于卷積神經網絡,提出了一種數據驅動的軌道車輛輪軌力識別方法,對軌道車輛直線和曲線工況的輪軌力進行了識別,并與幾種傳統的數據驅動方法進行了對比.曾俊瑋等[22]針對膠輪車輛輪胎載荷的識別,提出了一種卡爾曼濾波器與神經網絡相結合的模型,通過神經網絡修正卡爾曼濾波器的識別結果,提高了輪胎載荷的識別精度.

從已有的研究中可以看出,以往的研究大多使用單一方法進行輪軌力的識別,缺乏方法間對比和綜合評判;此外,運用機器學習修正物理模型,構建二者的聯合模型,是目前各學科領域研究的新熱點.具體到本文研究領域,學者們大多單獨運用時域法或機器學習方法對輪軌力進行識別,只有少數研究[22]將二者進行結合.針對現有研究存在的不足,本文基于軌道車輛的典型特征,選取了2 種具有代表性的時域動載荷識別方法,在10 自由度軌道車輛垂向動力學模型基礎上,對其垂向輪軌力進行識別;詳細對比2 種方法在計算速度、計算精度等方面的優劣;在此基礎上,針對物理時域方法所存在的識別誤差,引入機器學習算法,將NARX (nonlinear autoregressive models with exogenous inputs)模型作為誤差預測模型,對時域動載荷識別方法的識別誤差進行修正,進而嘗試提高動載荷的識別精度.本文方法旨在為后續的軌道車輛輪軌力識別,乃至列車運行安全性評估提供理論支撐.

1 時域動載荷識別方法

1.1 Green 函數法

加速度脈沖響應函數如下式所示[23]

通過脈沖響應函數公式,可以得到每一時刻的脈沖響應函數值,并由此計算得出振動系統的Green函數矩陣.對于單自由度系統,其響應正演表達式如下所示

式中,z為系統的響應向量,z={z1,z2,···,zm}T;F為系統所受的載荷向量,F={F1,F2,···,Fm}T;zi和Fi分別代表第i個時刻的響應值和載荷值;m為采樣點的個數;H為系統的Green 函數矩陣.式(2)可寫為如下的形式

式中,hi(i=1,2,···,m)為脈沖響應函數值;Δt為時間步長.

對于單自由度系統,其Green 函數矩陣的構建方法是,通過脈沖響應函數公式計算出各個時刻的脈沖響應函數值hi(i=1,2,···,m),令矩陣主對角線以上的元素的值為0,主對角線上的元素為 Δth1,從矩陣第1 列到第m列的元素,其值均從主對角線上的 Δth1開始,第1 列為 Δth1～Δthm,第2 列為 Δth1～Δthm-1,以此類推,直到第m列,其非零元素為主對角線元素 Δth1.

與單自由度系統不同,多自由度系統通過脈沖響應函數公式計算出的各個時刻的脈沖響應函數值hi(i=1,2,···,m)均為矩陣,因此多自由度系統的Green 函數矩陣可以看做眾多形同單自由度Green 函數矩陣的子矩陣的組合,各子矩陣中的元素分別為hi中對應位置的值與 Δt之積.多自由度系統的正演模型如下所示

式中,zi為第i個位置的響應列陣;Fi為第i個位置的載荷列陣;為載荷作用點i和響應測量點j之間的Green 函數矩陣;M和N分別為作用在系統上的動載荷個數和響應測量點的個數.為保證該線性方程組有解,需要滿足N≥M.

在正演模型建立完成后,通過對Green 函數矩陣求逆(或求廣義逆)來對動載荷進行識別,單自由度系統和多自由度系統的動載荷識別公式分別如下所示

1.2 狀態空間法

對于一個n自由度線性定常系統,其動力學方程如下所示

式中,M,C和K分別為系統質量、阻尼和剛度矩陣;,和x分別為系統加速度、速度和位移向量;f為外載荷向量.

將上式轉化為狀態空間方程的形式,為

由文獻[24]可知,一般的離散狀態空間方程只能通過位移和速度對動載荷進行識別,當已知系統加速度時,需引入Newmark 積分對狀態空間方程進行離散,有如下表達式

式中,Xi為狀態變量,此時的狀態變量由位移、速度、加速度向量組成,Xi=[xi,,]T.

式中,β 和 γ 為Newmark 積分參數,β 一般在0.25到0.5 之間選取,γ 在0 到1 之間選取[24].

由式(9)可得每一步的外載荷的求解表達式,如下所示

將式(10)展開,可得到下式

因此在已知加速度響應的情況下,通過式(10)求解外載荷在本質上就是通過式(11)～式(13)求解外載荷.

在剛度和阻尼矩陣中,并不是所有位置的響應都與外載荷的計算相關,為了提高方法的穩定性和精度,找到對外載荷fi+1的計算有影響的測點位置(即影響系數法的概念),把這些測點位置的加速度響應作為已知量,假設已知i時刻(初始時刻) 的位移、速度和加速度,根據式(11)和式(12)可以得到i+1 時刻的位移和速度,再根據式(13)即可求得i+1時刻的動載荷.對于i時刻位移和速度未知的情況,由初值引起的誤差將在后文中進行討論.該方法較適用于多自由度彈簧–阻尼–質量模型,如軌道車輛動力學模型.

文獻[25] 中給出了Wilson-θ反分析法在非0 初始條件下由初值引起的誤差,并引入多項式擬合趨勢項對位移和速度進行了修正.由于本文采用的Newmark 積分離散的狀態空間法同樣需要對加速度進行數值積分來間接計算速度和位移,可能會存在相同的問題,因此同樣需要分析非零初始條件下的初值誤差對識別結果的影響.

為了提高方法的穩定性和精度,同樣以對外載荷計算有影響的測點位置的加速度為輸入,若系統為非0 初始狀態,由下式所示

在1 時刻這些測點的位移實際值x1可由0 時刻的測點的位移x0、速度、加速度以及1 時刻的加速度表示,1 時刻的速度實際值可由0 時刻的速度、加速度以及1 時刻的加速度表示.

由于x0和未知,若此時仍將系統視為零初始狀態,則帶誤差的1 時刻的這些測點的位移和速度計算值分別為

令 δ11為第1 步的位移計算誤差,δ21為第1 步的速度計算誤差,則有

2 初值誤差分析與修正

繼續計算第2 時刻測點的位移、速度的實際值與計算值

令 δ12為第2 步的位移計算誤差,δ22為第2 步的速度計算誤差,則有

至此已經可以發現規律,即第k步的測點位移計算誤差 δ1k、速度計算誤差 δ2k分別為

要確定趨勢項,就需要求得一組pk使得I值達到最小,由多元函數求極值的必要條件可得

其中j=0,1,2,···,m,即

將其表示為矩陣形式,如下式所示

可以證明,方程組系數矩陣是一個對稱正定矩陣,故存在唯一解.通過上式求解出pk,從而可得擬合多項式.

除了初值誤差引入的趨勢項之外,相關研究[26-27]也表明,對于由信號本身或其他因素所引起的積分信號的曲線趨勢項,多項式擬合修正的方法同樣也是有效的.

3 基于NARX 模型的動載荷識別誤差修正

采用基于純物理模型的時域法對動載荷進行識別時,難免會因為各種因素的影響(如響應觀測不全,觀測噪聲等)造成識別誤差.為了減小識別誤差,參考相關文獻[22,28]中提出的物理–機器學習相結合的模型思路,本節引入NARX 模型,利用其強大的非線性逼近能力,通過一段已知的輸入–輸出時間歷程對模型進行訓練,對基于物理模型時域法的動載荷識別誤差進行預測,進而嘗試對識別誤差進行修正,從而提高動載荷識別精度.這樣既避免了純機器學習模型缺乏物理解釋的問題,又減小了純物理模型的識別誤差.

NARX 模型是線性ARX (autoregressive models with exogenous inputs)模型的擴展,與靜態回歸模型相比,增加了多步時延的環節,并引入了非線性映射函數,因此NARX 模型具有動態特性,可以利用輸入、輸出的歷史信息來對具有復雜映射關系的未知時間歷程進行預測.對于一個單輸入單輸出系統,其NARX 模型可以表示為

式中,f(t) 為t時刻的系統輸出;z(t) 為t時刻的系統輸入;na為輸出的階數;nk為輸入相對于輸出延遲的階數;nb為輸入的階數;F(·)為非線性映射函數,常用的有小波網絡、S 型網絡、二叉樹回歸模型、支持向量機等.由于小波網絡具有結構簡單、收斂速度快及計算精度高的優點,故本文的F(·)選用小波網絡[29].

具體到本文而言,由于要使用軌道車輛軸箱響應來預測垂向輪軌力的識別誤差,因此本文采用的NARX 模型的輸入為軌道車輛軸箱響應,輸出為垂向輪軌力的識別誤差,定義識別誤差為物理模型時域法的識別值減去輪軌力的真實值(可以含隨機噪聲),具體的NARX 模型可以表示為框圖的形式,如圖1 所示.

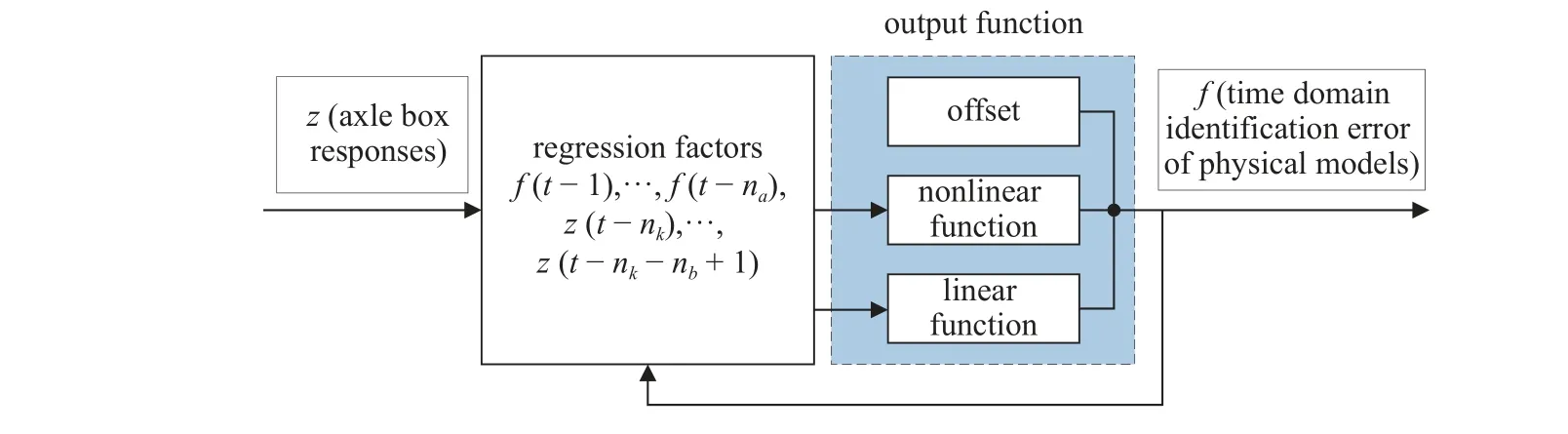
圖1 NARX 模型示意圖Fig.1 Schematic diagram of NARX model

采用NRMSE適應度來評價NARX 模型的預測精度,如下式所示

式中,f為目標輸出;為目標輸出的均值;為模型的預測輸出.

在使用訓練集的輸入輸出以及測試集的輸入得到NARX 模型的識別誤差預測值之后,以測試集的響應輸入得到物理模型時域法的識別結果,再將該識別結果減去識別誤差預測值即為修正后的動載荷識別值,其框圖如圖2 示.

當非線性映射函數確定之后,輸出的階數na、輸入相對于輸出延遲的階數nk以及輸入的階數nb將影響NARX 模型的預測效果,參數的選取將在下一節進行討論.

4 軌道車輛垂向輪軌力識別

根據《車輛?軌道耦合動力學》[30],車輛垂向動力學模型由車體、前后轉向架和4 個輪對組成.對于車體以及前后轉向架,考慮浮沉運動和點頭運動;對于4 個輪對,考慮浮沉運動,總計10 個自由度,如圖3 所示.在本研究中,根據該模型進行動力學建模,以軸箱加速度響應為輸入,對輪軌垂向力進行識別.通過建立車輛垂向動力學微分方程,可以提取出該系統的質量M、剛度和阻尼矩陣K,C,外載荷向量如下.

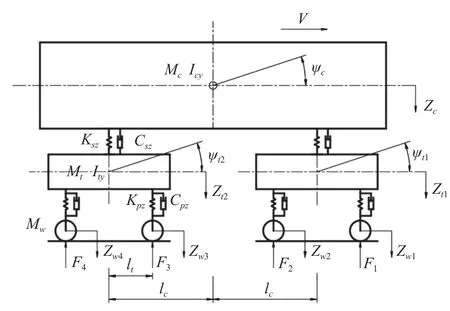
圖3 軌道車輛垂向動力學模型Fig.3 Vertical dynamic model of rail vehicles

式中,Mc為車體質量;Mt為構架質量;Mw為輪對質量;Icy為車體繞Y軸轉動慣量;Ity為構架繞Y軸轉動慣量;Ksz為轉向架一側二系懸掛垂向剛度(N/m);Kpz為每軸箱一系懸掛垂向剛度(N/m);Csz為轉向架一側二系懸掛垂向阻尼(N·s/m);Cpz為每軸箱一系懸掛垂向阻尼(N·s/m);F為外載荷向量,F1,F2,F3和F4分別為第1 輪對、第2 輪對、第3 輪對和第4 輪對輪軌垂向動載荷;lc為車輛定距之半;lt為車輛固定軸距之半.

采用通用動力學仿真軟件建立具有同等懸掛參數的軌道車輛多體動力學模型,采樣頻率為1000 Hz,得到仿真模型在一段隨機高低不平順軌道激勵下以250 km/h 速度行駛時的4 個輪對的垂向輪軌動載荷和軸箱垂向加速度響應,在此以第1 輪對為例,截取非零初始條件下的4000 組采樣點作為測試集,另取10 000 組采樣點作為訓練集,如圖4 所示.采用Pearson 相關系數來評價方法的識別精度,如下式所示[14]

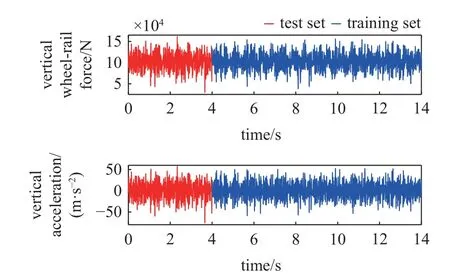
圖4 第1 輪對垂向輪軌力及加速度時間歷程Fig.4 Time history of vertical wheel-rail force and acceleration of the first wheelset

式中,n為采樣點的數目;為識別載荷;為識別載荷的均值;Pi為外載荷;為外載荷的均值.

考慮到以往的相關研究均直接使用仿真正演的加速度響應作為模型輸入,而實際上,在進行加速度響應的觀測時難以避免地會存在觀測噪聲,為了模擬實際,在本文算例的軸箱加速度響應中添加5%的隨機噪聲.分別使用Green 函數法和狀態空間法對輪軌垂向力進行識別,并對比識別精度與計算速度,如表1 所示,2 種方法對第1 輪對的識別結果對比如圖5 所示.

表1 2 種時域法對垂向輪軌力的識別結果對比Table 1 Comparison of the two time domain methods for identifying vertical wheel-rail forces

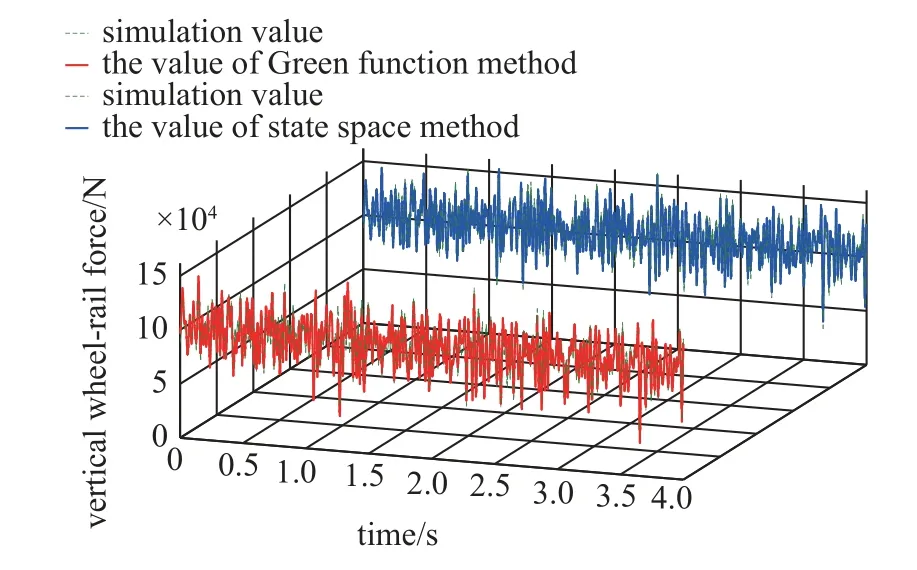
圖5 2 種方法對第1 輪對垂向輪軌力的識別結果對比Fig.5 Comparison of the two methods for identifying the vertical wheel-rail force of the first wheelset

從表1 中可以看出,在計算時間方面,狀態空間法具有較快的計算速度,對4 s 時間歷程的識別計算時間在0.5 s 左右,而Green 函數法因為需要建立規模較大的Green 函數矩陣并對其進行求逆,因而計算效率較低,計算時間達到了19 s 左右;在計算精度方面,2 種方法識別值與仿真值的Pearson 相關系數均大于0.91,對應極強相關性,說明2 種方法均能較好地識別出輪軌垂向力.但從圖5 中可以看出,識別值與仿真值的波形在一些位置的對應較差,識別效果還有一定的提升空間,因此引入NARX 模型對識別誤差進行修正,并對2 種方法的識別誤差進行提取.考慮到篇幅的限制,在后文中只針對第一輪對進行修正,其余輪對的修正步驟與之相同,不再進行展開.

為了使結果更具一般性,同時考察模型對噪聲的抵抗能力,在訓練集和測試集的軸箱加速度與識別誤差中也引入5%的隨機噪聲以模擬實際觀測噪聲.對于Green 函數法,由于載荷識別結果僅與加速度有關,因此使用軸箱加速度作為誤差預測模型的輸入即可;而對于狀態空間法,經試算發現直接使用軸箱加速度來預測載荷誤差較為困難,預測效果差,分析其原因可知,這種方法的載荷識別結果與加速度、速度和位移均有關,所用到的速度、位移是由加速度間接計算得到的,由于軸箱加速度本來就是非平穩信號,其中還含有噪聲,因此間接計算得到的位移即使在使用更高次的多項式擬合趨勢項修正后仍然存在一定的誤差,而經間接計算得到的速度誤差較小,因此位移所含的誤差對載荷識別結果的影響相對更大,故選取計算并修正后得到的軸箱位移作為該方法誤差預測模型的輸入.在進行修正之前,還需要尋找NARX 模型的誤差預測效果和輸入階數nb、輸出階數na以及輸入相對于輸出延遲的階數nk的關系.需要進行說明的是,一般的機器學習研究對于模型超參數的選取常在驗證集進行,而本文研究的重點主要是提供算法思路并驗證其可行性,而不是超參數的選取,故沒有再設置驗證集,而是在測試集進行參數選取.事實上,本文測試集起到的是驗證集的作用,后續如需進一步驗證模型的泛化能力,再另外選取新的測試集進行測試即可.

在本例中,暫不考慮nk的影響,只通過改變輸入階數nb、輸出階數na來達到一個較好的誤差預測效果.同樣以第一輪對為例,設置na,nb的值以5 為步長遞增,為了防止輸入輸出階數過大而導致的訓練發散,將其最大值設置為150,觀察測試集的NRMSE適應度隨著na和nb值增加的變化情況,如圖6 所示.

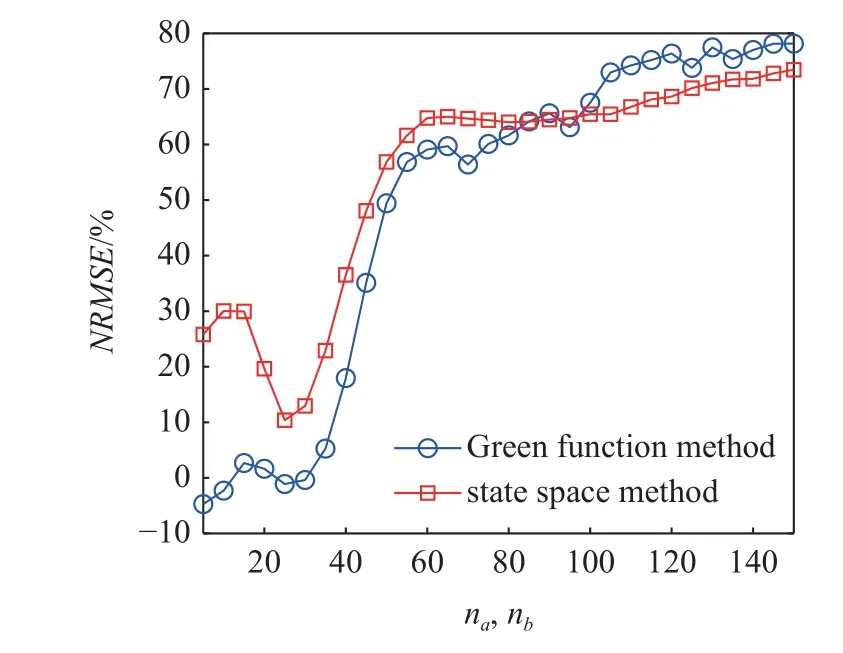
圖6 測試集預測誤差NRMSE 適應度隨na 和nb 值的變化關系Fig.6 The relationships between the NRMSE of predicted error and the values of na and nb in the test set

從圖6 中可以看出,2 種方法預測誤差的NRMSE適應度隨著na和nb值的增大,整體呈現出增大的趨勢,當na和nb值達到60 左右時,NRMSE值增長趨勢變緩,且均大于50%.根據圖中呈現的關系,選取2 種方法的na和nb均為150,2 種方法在測試集的誤差原始值(含5% 隨機噪聲) 和預測值如圖7 所示,對應的NRMSE適應度如表2 所示.

表2 預測誤差的NRMSE 適應度Table 2 NRMSE of the predicted error

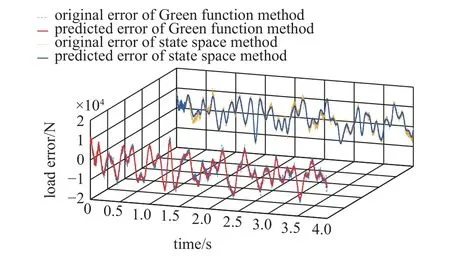
圖7 測試集的誤差原始值(含5%隨機噪聲)和預測值Fig.7 The original error (including 5% random noise) and the predicted error in the test set

從圖7 中可以看出,NARX 模型能較好地預測2 種方法的誤差趨勢,在訓練集識別誤差帶5%隨機噪聲的情況下,仍然能較準確地預測出2 種方法的識別誤差,具有一定的抗噪能力,NRMSE適應度均大于73%.將圖7 中的誤差預測值記為err,用于修正圖5 中的垂向輪軌力識別值(記為F*),則有輪軌力最終識別值F為

經修正后的輪軌力最終識別值F如圖8 所示.

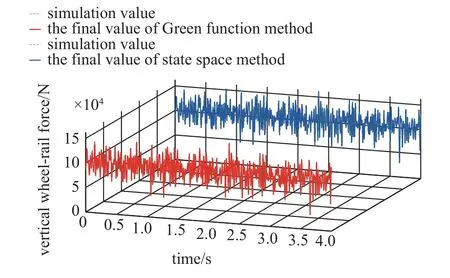
圖8 最終識別值對比Fig.8 Comparison of the final identification values

從圖8 中可以看到,經NARX 誤差預測模型修正后的2 種方法對第一輪對的最終識別結果均能很好地逼近原始載荷,識別誤差得到了很好的消除,其Pearson 相關系數分別為0.998 和0.997,對應極強相關性,相對于未修正的結果而言,Pearson 相關系數分別提升了0.050 和0.039.可見,本文所采用的時域法結合NARX 誤差修正的動載荷識別模型能很好地識別軌道車輛垂向輪軌力,并具有一定的抗噪能力.

5 結論

本文采用基于NARX 模型的機器學習方法對兩種常用的動載荷時域識別方法進行修正,在對兩方法計算速度、計算精度對比的基礎上,完成了軌道車輛垂向輪軌力的識別,主要得到以下結論.

(1) 提出了經典時域法結合機器學習修正的動載荷識別方法,基于兩種方法對軌道車輛垂向輪軌力進行識別,通過機器學習方法修正后的載荷識別誤差明顯減小,顯著提高了輪軌力的識別精度.

(2) 基于Green 函數法和狀態空間法的軌道車輛垂向輪軌力識別值與正演值的Pearson 相關系數大于0.91,但兩方法的識別精度均還有提升空間;在計算效率方面,狀態空間法對4 s 樣本的識別計算時間在0.5 s 左右,具有較快的計算速度,而Green 函數法由于需要建立較大規模的Green 函數矩陣并對其進行求逆,因而計算效率較低,計算時間達到了19 s 左右.

(3) 針對兩種方法的誤差產生原因,引入基于NARX 模型的機器學習方法,通過對兩方法識別誤差的訓練和預測,修正原始識別結果.研究結果表明: 采用NARX 模型修正時域法識別誤差的這一模式具有一定的可行性,可以較好地消除由響應觀測不全、隨機噪聲等因素引起的輪軌力識別誤差.經修正后,2 種方法對第1 輪對的最終識別值與仿真值的Pearson 相關系數均大于0.99,識別精度得到了較大的提高,說明本文方法為時域法識別精度的進一步提高提供了一種思路,具有一定的工程應用價值.

在后續的研究中,還可以考慮對軌道車輛橫向輪軌力以及帶有部分懸掛參數非線性的軌道車輛模型的輪軌力進行識別,進一步研究本文方法在更復雜的模型中的載荷識別能力.