壓電智能功能梯度夾芯結構高精度理論模型與主動控制1)

張欣宇 肖玉善 吳 振,?,2) 任曉輝

* (西北工業大學航空學院,西安 710072)

? (強度與結構完整性全國重點實驗室,西安 710065)

** (西安航空學院機械工程學院,西安 710065)

引言

梯度功能材料(functionally graded material,FGM)是兩種或多種材料復合成組分和結構連續梯度變化的一種新型復合材料,其材料性能在某一方向上連續梯度變化,消除了明顯的界面和性能突變,在工程結構中的應用越來越廣泛.作為智能材料,壓電材料以獨有的正逆壓電效應,廣泛應用在電聲學、傳感器技術、噪聲控制、微型機電系統、結構振動控制和柔性結構的主動控制等領域[1-2].因此,將FGM 與壓電材料相結合而產生的智能結構和材料,引起了各國學者的廣泛關注.

目前,國內外學者對壓電智能結構的靜力學和動力學[3-4]等問題做了一系列的研究工作.對于壓電層合結構的力學問題,Ray 等[5-6]給出了精確解.此外,三維有限元方法[7-11]也被廣泛運用.然而對于多層結構,三維分析方法要劃分大量網格,計算效率低.因此,Pablo 等[12-13]在經典層合板理論的框架下提出了不需考慮電自由度的壓電層合結構有限元方法;Malikan[14]基于一階剪切變形理論(first-order shear deformation theory,FSDT)研究了壓電功能梯度板的力電剪切屈曲問題;基于三階剪切變形理論,Ngoc-Tu等[15]提出了一種分析含壓電功能梯度多孔材料振動的方法和基于位移和速度反饋的閉環控制算法;此外,分層理論(layerwise theory)也被用于壓電層合結構的研究[16-18],這種理論可以精確地獲取結構的層間應力,但其自由度會隨著層數增加而上升,從而嚴重影響計算效率.因此,Li 等[19]發展的整體?局部高階理論(global-local higher-order theory,GLHT)消去了依賴于層數的自由度,在保證精度的前提下,提高了計算效率.Beheshti-Aval 等[20]基于GLHT預測了壓電層合梁剪切行為,雖然該模型未知參數僅比FSDT 多一個,但對厚梁的計算精度更高.

Li 等[21]利用雙向B 樣條有限元法推導了壓電層合板的位移和應力解,在分析中厚板時效果很好;Wu 等[22]構造了一種滿足單元間C1弱連續的三角形精化單元,避免了剪切閉鎖的同時可以很好地預測壓電層合結構的力電行為;Ray[23]構建了基于分層理論的無網格法,實現了壓電智能結構的靜力分析,但無法準確分析由于壓電致動器的橫向致動引起的響應.考慮到GLHT 理論中位移函數存在橫向位移的一階導數,需要滿足單元間C1連續條件,而等幾何方法[24](isogeometric analysis,IGA)將計算機輔助幾何設計中用于表達幾何模型的非均勻有理B 樣條(non-uniform rational B-splines,NURBS)的基函數作為形參數,實現了任意階次的平滑性,可以方便地求解薄板殼等高階連續問題.等幾何分析方法已用于靜力、振動和裂紋擴散等模型的分析[25-27].Nguyen 等[28]研究了材料性質和外部條件對梯度壓電材料多孔板固有頻率的影響;Phung 等[29]進行了智能壓電功能梯度材料板的非線性瞬態分析;Akbar等[30]計算了壓電層合板通過結構振動獲得的能量.

已有研究表明,整體?局部高階理論和分層理論具有較高精度[16,22].在使用整體?局部高階理論構造有限元方法時,應變中包含撓度的一階導數和二階導數,需要構造滿足單元間C1連續的橫向位移函數[22],而等幾何分析方法很好地解決了C1連續問題[31].因此,針對含壓電層的層合結構和含壓電層的功能梯度夾芯結構,本文用Reddy 型整體?局部高階理論模擬結構位移場,用Layerwise 分層理論模擬結構沿厚度方向電勢,構造了可準確分析結構力電行為的精化模型.結合等幾何分析方法,分析了壓電層的層合結構的彎曲行為.此外,探究了含壓電層的功能梯度夾芯結構在力電載荷作用下,功能梯度系數和鋪層角度對結構彎曲行為的影響規律.最后,構建了含壓電層的功能梯度結構的速度閉環控制系統,通過調整速度反饋增益(Gv),實現了對無阻尼壓電功能梯度結構的振動主動控制.

1 理論方法

1.1 Reddy 型整體?局部高階理論

在Li 等[19]發展的1,2-3 整體?局部高階理論中,結構的任一層位移函數可以分解為整體位移分量以及局部位移分量.通過將局部位移函數引入Reddy理論[32]面內位移場,可以將Reddy 型整體?局部高階理論的初始位移場表示為

其中,上標k表示結構第k層,下標G表示整體位移分量,下標L表示局部位移分量.對于夾芯結構,其整體坐標系以及結構示意圖如圖1(a)所示,局部坐標系如圖1(b)所示.

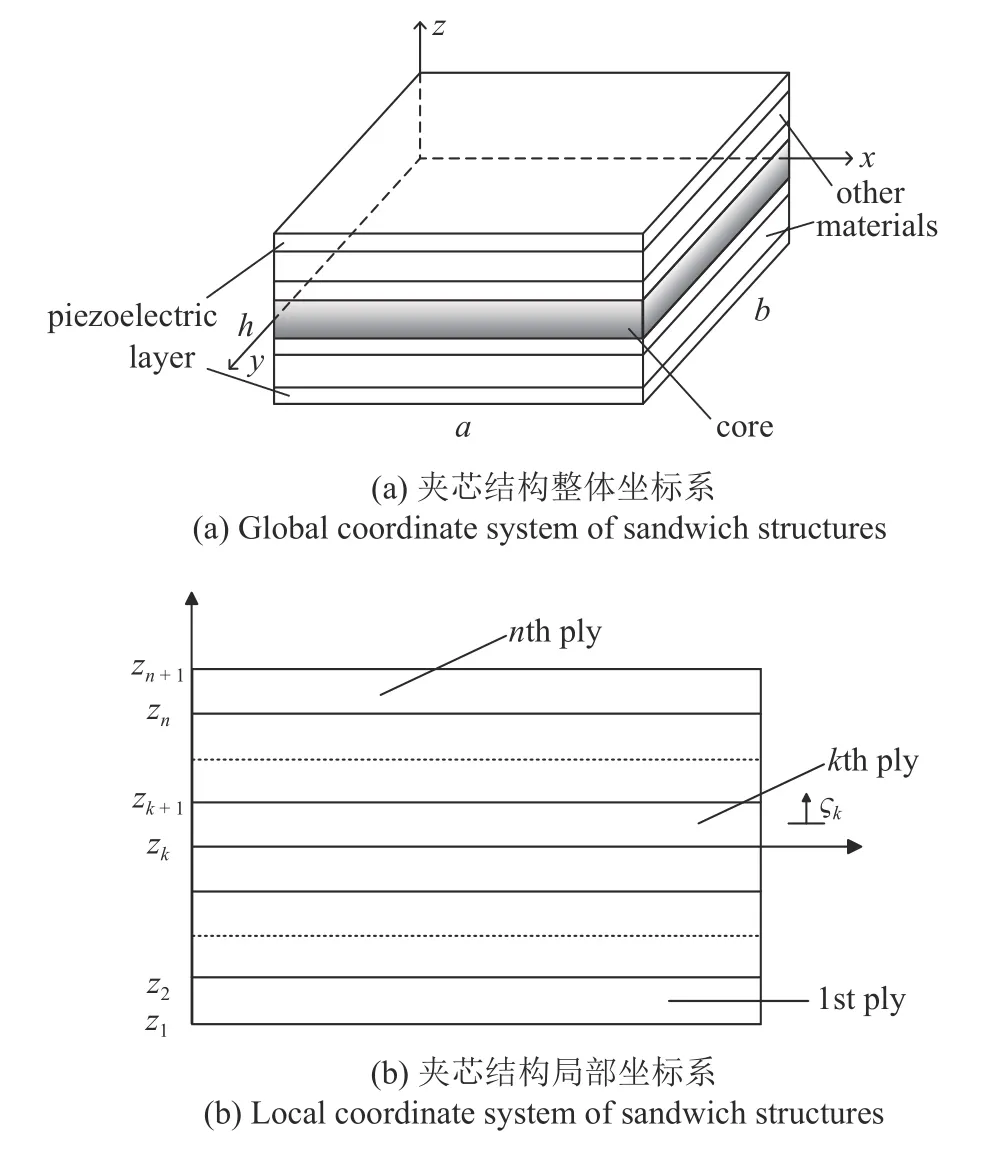
圖1 夾芯結構的整體和局部坐標系Fig.1 Global and local coordinate system of sandwich structures

整體位移分量采用Reddy 理論位移模式

面內局部位移分量沿厚度方向每層截取3 次

其中

從初始位移函數可以看到,當前模型共包含6n+5 個獨立未知變量.為使得最終的位移函數中未知變量的數目獨立于夾芯板層數,依次施加面內位移連續性條件,橫向剪切應力連續條件以及上下表面自由邊界條件,可以消去共6n?2 個未知變量.最后得到可分析任意鋪層角度夾芯板的Reddy 型整體?局部高階理論的最終位移函數[33]

根據最終位移模式和幾何方程,夾芯板第k層應變可表示為

1.2 Layerwise 理論

對于薄壓電層,可假設電位移沿厚度方向分段線性分布[18].因此,zi和zi+1之間的電勢可以寫為

且沿厚度方向全部電勢可以表達為

?i+1(x,y) 是z=zi+1處電勢,?i(x,y) 是z=zi處電勢.

1.3 壓電功能梯度板本構方程

假設材料屬性P,如彈性模量和泊松比等,沿功能梯度板厚度方向呈指數變化[34]

其中P1為功能梯度板的上表面材料屬性,P2為功能梯度板的下表面材料屬性,n為功能梯度系數,h為功能梯度板的總厚度.

基于平面應力條件 σz=0,壓電材料在其材料軸系(1,2,3)中的本構方程可以表示為

其中,σi,Di分別是應力和電位移;εi,Ei分別是應變和電場;Cij,kij和eij分別是壓電材料的彈性常數、介電常數和壓電常數.其中

電場強度與電勢關系為

結合彈性力學轉軸公式,可得偏軸彈性矩陣Qs,則整體坐標系下(x,y,z)的本構方程如下

式中T為坐標轉換矩陣[35],其中

2 等幾何分析方法

2.1 NURBS 函數

在一維情況下,第i個p階B 樣條基函數定義為

二維情況下的B 樣條基函數,可由兩個方向張量 [ξ0,ξ1,···,ξn+p] 和 [η0,η1,···,ηn+p] 的張量積構成

在B 樣條函數的基礎上,進一步構造 NURBS函數[24],可表示為

2.2 電勢場離散化

第i層的電勢可表示為

將式(18)代入式(7)和式(12)可得

2.3 位移場離散化

夾芯板的幾何形狀xh和位移場uh可描述為

其中PA是控制點坐標,qA為控制點A自由度向量

將式(19)代入式(5)可得到應變為

其中BdA為A點處的幾何矩陣,具體形式如下

2.4 控制方程和剛度矩陣

根據Hamilton 原理,在某一時間間隔t1和t2內所有可能發生的位移中,真實位移會使得壓電智能結構的Lagrange 函數取極小值

其中,T為結構的動能,U為結構應變能和電能,W為面力和電場所做的功.

對式(22)變分,結構控制方程可以表示為

其中F為力載荷,Qφ為壓電層表面電載荷,Kd為剛度矩陣,Kφd=KdφT為力電耦合剛度矩陣,Kφ為介電剛度矩陣,具體可表示為

M表示質量矩陣[36],可表示為

聯立式(23)和式(24)消去電勢得

考慮等效瑞利阻尼[37]

其中 α和β 為瑞利阻尼參數,可由試驗獲取.將式(33)引入式(30),得

2.5 閉環主動控制

壓電功能梯度夾芯板結構如圖2 所示,結構頂層作為壓電致動器,底層作為壓電傳感器,則式(24)可改寫為

圖2 夾芯結構主動控制系統Fig.2 Active control system of sandwich structures

其中下標s代表傳感器層,下標a代表致動器層.

當夾芯板處于振動狀態時,傳感器層的變形將通過壓電效應產生電荷形成輸出電壓,通過放大器放大后,信號將被反饋到驅動器層中.由于逆壓電效應,致動器層會產生反驅動力來抑制結構的變形,從而實現結構閉環電路主動控制[38].

對于傳感器層,由于沒有額外施加外部電荷,傳感器層因壓電效應所產生的電勢和電荷分別為

通過閉環電路的反饋,致動器層產生的電勢為

式中,Gd和Gv分別為位移和速度反饋增益.將式(39)代入式(35)中,可得致動器層電荷為

最后將式(35)～式(36)、式(38)和式(40)代入式(34)中,得

3 彎曲行為分析和變形主動控制

本章首先分析了壓電層合板的彎曲行為,以驗證精化高階理論模型的有效性.隨后探究了壓電功能梯度層合板的鋪層角度和功能梯度系數對結構彎曲的影響.最后對壓電功能梯度結構進行了振動主動控制.算例中,簡支邊界條件和固支邊界條件的具體形式如表1 所示.

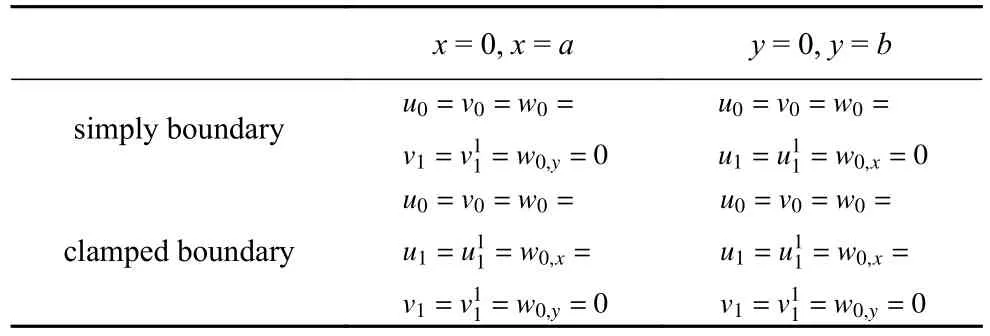
表1 邊界條件具體形式Table 1 The specific form of boundary conditions

3.1 壓電層合板彎曲行為分析

復合材料層材料屬性:E1=172.5 GPa,E2=E3=6.9 GPa,G23=1.38 GPa,G12=G13=3.45 GPa,v12=v13=v23=0.25,k11=k22=k33=8.85×10?12C2/N·m2.壓電層材料屬性:Ex=Ey=Ez=2 GPa,vxz=vyz=vxy=0.29,k11=k22=k33=1.06×10?12C2/N·m2,e31=e32=?0.004 6 C/m2,e33=e24=e15=0 C/m2.

分別計算3 種跨厚比(a/h=4,10,100)和兩種力?電載荷加載形式下(qu0=1 Pa,qe0=0 V 和qu0=1 Pa,qe0=100 V)壓電層合板上表面中心點撓度,并做無量綱化處理

圖3 為本文模型計算的撓度收斂情況(a/h=4),使用13×13 網格,本文提出的等幾何分析結果已收斂.因此,后續均使用13×13 網格進行分析.

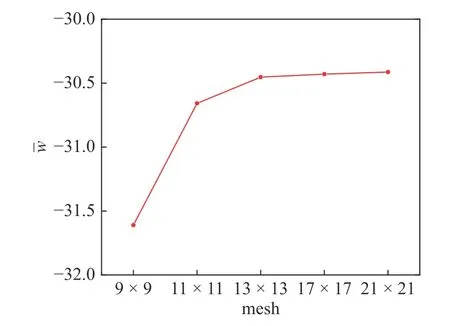
圖3 不同網格上表面中心點撓度收斂性Fig.3 Convergence of the deflection at the center point of top surface using different meshes

為公平比較,在同一計算機上(處理器為Intel(R)Core(TM) i7-9700 CPU @3.00GHz)基于FSDT 的等幾何分析方法(FSDT-IGA,網格為13×13)計算了壓電層合板(a/h=10)的撓度,同時給出了基于本文模型等幾何分析方法的結果(網格為13×13),并提供了對應的計算時間.Ray 等[6]已經給出了三維精確解,Song 等[39]給出了FSDT 模型的分析結果,如表2 所示.結果表明: 在跨厚比為10 時,基于FSDT等幾何分析方法的結果(剪切修正系數為5/6) 和Song 等[39]的分析結果相近.在0 和100 V 電壓作用下并使用相同的網格(13×13),基于FSDT 等幾何分析方法計算時間比本文等幾何分析方法計算時間快7.69 和7.74 s,但精度低于本文模型.

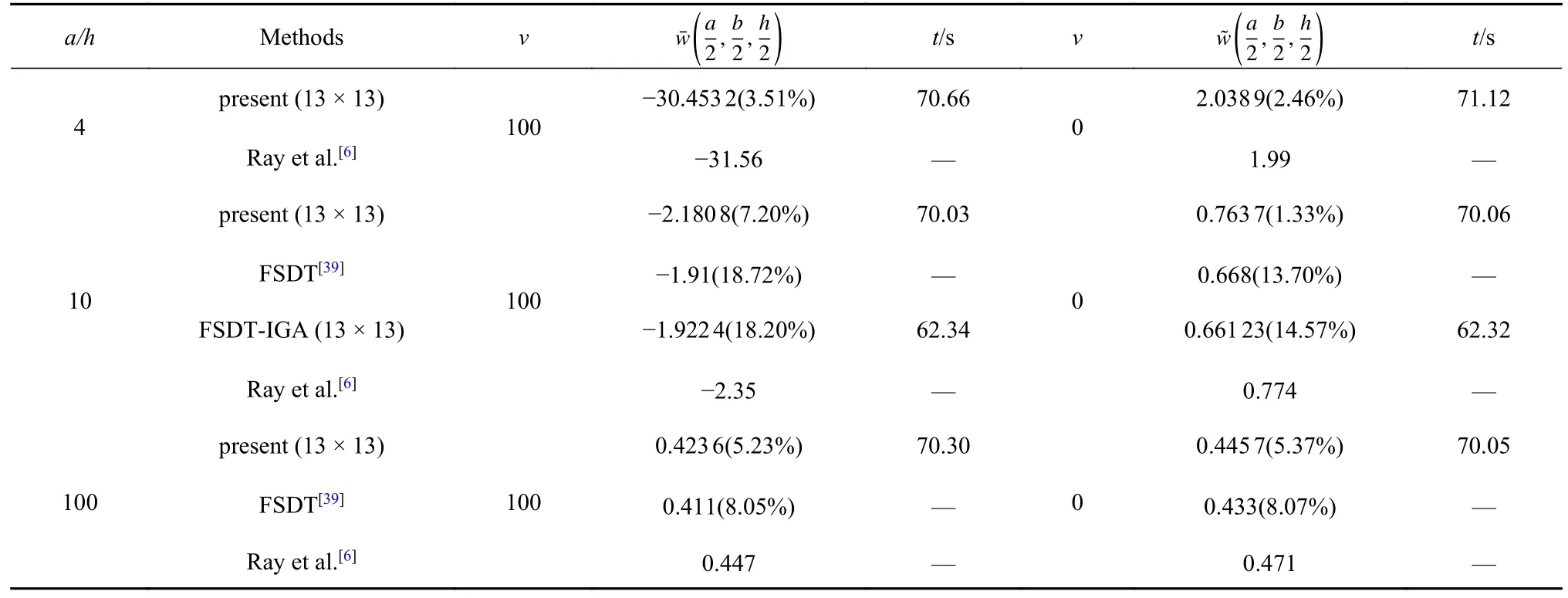
表2 壓電層合板上表面中心點撓度Table 2 The deflection of the top surface center point of piezoelectric laminated plates

可以發現,與FSDT 模型計算結果相比,精化高階理論模型明顯有更高的精度,這在計算中厚板時更加明顯,具體表現為: (1) 在計算跨厚比為4 的結構上表面中心點撓度時,FSDT 模型未給出結果,而本模型的最大誤差僅為3.51%;(2)在計算跨厚比為10 的結構上表面中心點撓度時,FSDT 模型的最小誤差為13.70%,而本模型的最大誤差僅為7.2%;(3)在計算跨厚比為100 的結構上表面中心點撓度時,FSDT 模型的最小誤差為8.07%,而本模型的最大誤差僅為5.37%.

3.2 壓電功能梯度板靜態彎曲分析

本節以四邊簡支的5 層壓電功能梯度層合方板為例,探究功能梯度系數n和鋪層角度對結構彎曲行為的影響.結構形式為 (P/CFRP/FGM/CFRP/P),其中P 代表壓電層,CFRP 代表復合材料層,FGM表示功能梯度層.中芯層為由Ti-6Al-4V 和氧化鋁組成的功能梯度層;上下兩層為壓電層;在壓電層與功能梯度層之間各鋪設一層復合材料.結構中復合材料層和功能梯度層3 層厚度均為3 mm,兩個壓電層的厚度均為0.04 mm,跨厚比a/h=4.在結構上表面施加50 V 的均布電壓和1000 MPa 的均布載荷,下表面接地.壓電層和復合材料層的材料屬性[22]如下所示.

壓電層材料常數:C11=238 GPa,C22=23.6 GPa,C33=10.6 GPa,C44=4.4 GPa,C55=2.15 GPa,C66=6.43 GPa,C12=3.98 GPa,C13=2.19 GPa,C23=1.92 GPa,k0=8.85×10?12C2/N·m2,k11/k0=12.5,k22/k0=11.98,k22/k0=11.98,e31=?0.13 C/m2,e32=?0.14 C/m2,e33=?0.28 C/m2,e24=e15=?0.01 C/m2.復合材料層材料常數:C11=134.9 GPa,C22=14.35 GPa,C33=14.35 GPa,C12=5.156 GPa,C13=5.156 GPa,C23=7.133 GPa,C44=5.654 GPa,C55=3.604 GPa,C66=5.654 GPa,k0=8.85×10?12C2/N·m2,k11/k0=3.5,k22/k0=3,k22/k0=3.Ti-6Al-4V:E=105.7 GPa,v=0.298 1,ρ=4429 kg/m3.氧化鋁:E=320.24 GPa,v=0.26,ρ=3750 kg/m3.

圖4 研究了功能梯度系數n(0～50)和復合材料鋪層角度對(0～π/4)結構彎曲行為的影響.結果表明: (1)當復合材料鋪層角度不變,隨著功能梯度系數n逐漸增大,中心點撓度逐漸減小;(2) 當功能梯度系數n不變,隨著復合材料鋪層角度逐漸增大,中心點撓度逐漸減小;(3) 當功能梯度系數n在0～5之間時,功能梯度系數n對結構彎曲行為的影響比鋪層角度對結構彎曲行為的影響更顯著.

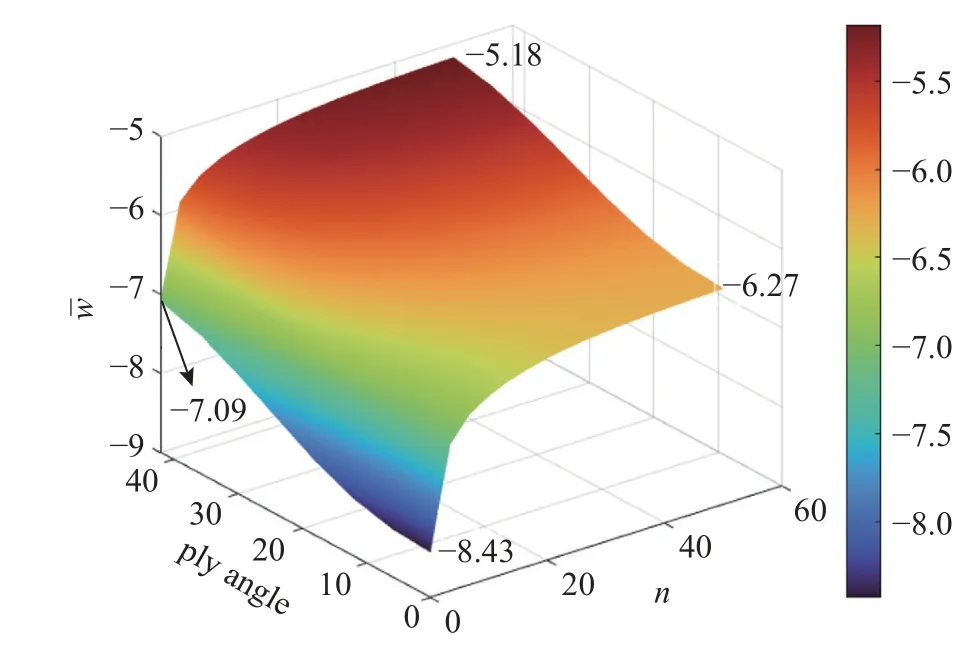
圖4 上表面中心點撓度隨鋪層角度和功能梯度系數變化Fig.4 The variation of the deflection of the top surface center point with ply angles and functional gradient coefficients

3.3 壓電功能梯度板變形主動控制分析

本節分析了四邊固支壓電功能梯度夾芯方板的變形主動控制.方板結構形式可表示為(P/FGM/P).方板尺寸為200 mm×200 mm×24 mm,其中功能梯度層厚度為20 mm,材料屬性與3.2 節的功能梯度層一致,功能梯度系數n=2;功能梯度層上下表面鋪設了厚度為2 mm 的壓電層,材料為PZT-G1195N[40],材料屬性如下.

定義4 種時變載荷,分別為階躍載荷、三角型載荷、正弦型載荷和爆炸沖擊載荷

其中,qt0=1000 Pa,t0=1.0×10?3s.

4 種載荷的時變函數圖像如圖5 所示.1.0×10?3s前,結構處于強迫振動階段,此后進入自由振動.不考慮結構的瑞利阻尼,通過改變結構速度反饋增益Gv來調節結構主動阻尼.

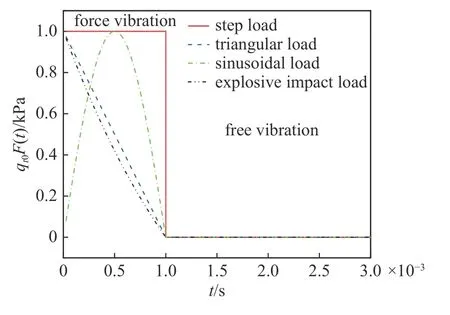
圖5 4 種不同的時變函數Fig.5 Four different time-varying functions

結構上表面中心點動態撓度的控制效果如圖6所示.結果表明: (1)當Gv=0 時,由于結構本身未考慮阻尼,結構將以當前時刻對應的靜態撓度為平衡位置,無衰減地持續著強迫振動和自由振動,且自由振動階段的幅值取決于強迫振動結束時刻系統的能量;(2)當Gv不為0 時,由式(42)可知結構引入了主動阻尼,結構將以當前時刻對應的靜態撓度為平衡位置,做逐漸衰減的強迫振動和自由振動,完全衰減后,上表面中心點的撓度為當前加載狀態下的靜態撓度;(3)隨著Gv增大,由式(42)可知主動阻尼也增大,結構震蕩的振幅在一個震蕩周期內下降更多,完全衰減所需時間減少.這表明可以結合實際情況,調整控制系統的速度反饋增益Gv的大小,實現對結構震蕩的主動控制.

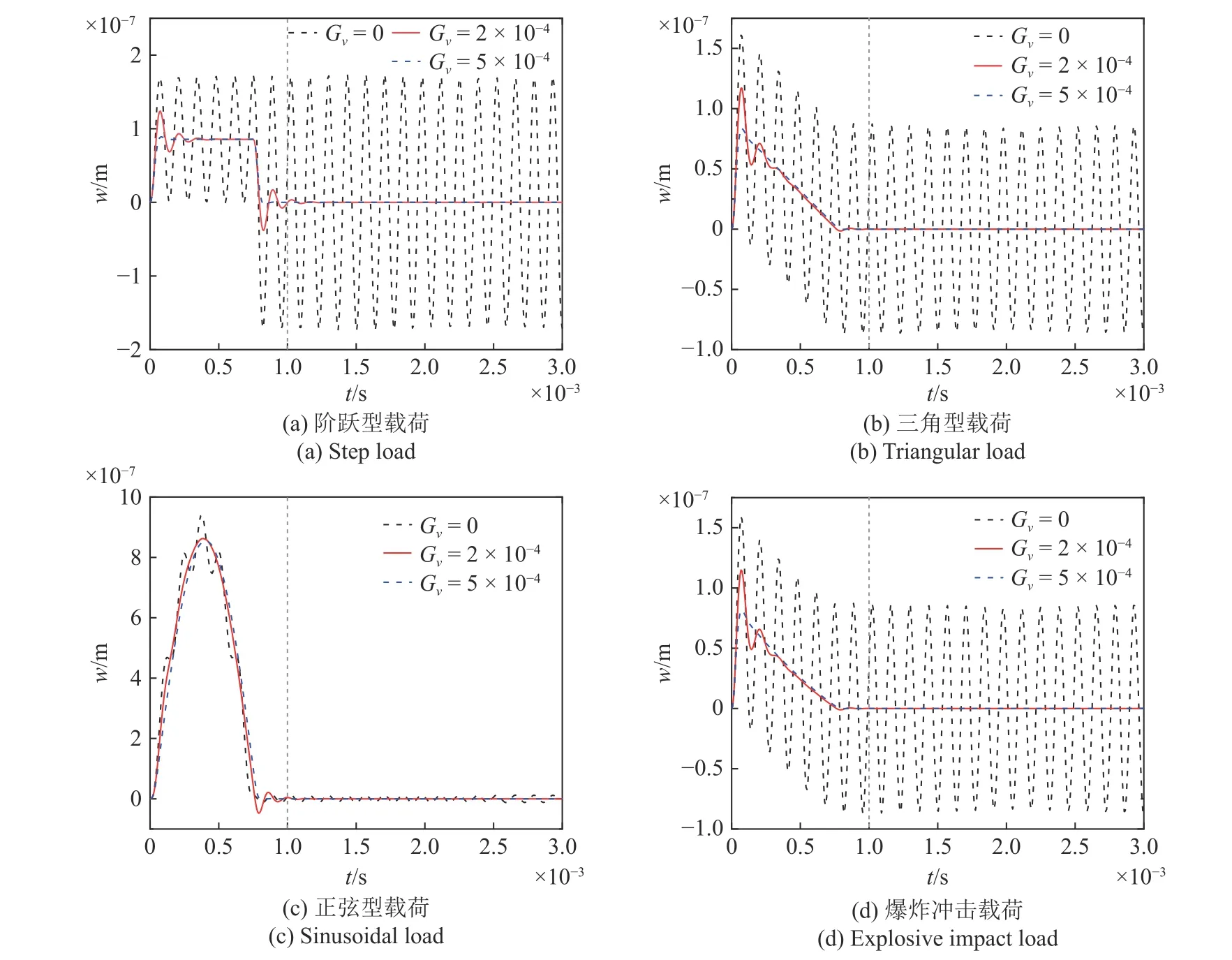
圖6 4 種載荷不同Gv 下對上表面中心點撓度的主動控制效果Fig.6 The active control effect of different Gv on the deflection of the top surface center point under four different loading conditions

4 總結

本文針對含壓電層的層合結構和含壓電層的功能梯度結構力學問題發展了一種高精度的數值計算方法.首先結合Reddy 型整體?局部高階理論和Layerwise 理論,發展了可準確分析含壓電層的層合結構和含壓電層的功能梯度夾芯結構力電行為的精化高階理論和等幾何分析方法.之后對壓電層合板在力電載荷下的彎曲行為進行了分析,并與精確解和有限元解進行了對比,驗證了本文模型的有效性.隨后,探究了壓電功能梯度層合板在力?電載荷作用下,功能梯度系數和鋪層角度對結構彎曲行為的影響規律.最后,構建了壓電功能梯度板的速度閉環控制系統,對無阻尼壓電功能梯度結構進行了振動主動控制.本文得到主要結論如下.

(1)壓電功能梯度層合板在力電載荷下,當鋪層角度不變,隨著功能梯度系數逐漸增大,中心點撓度逐漸減小;當功能梯度系數不變,隨著鋪層角度逐漸增大,中心點撓度逐漸減小;當功能梯度系數在0～5之間時,功能梯度系數對結構彎曲行為的影響比鋪層角度對結構彎曲行為的影響更顯著.

(2)無阻尼壓電功能梯度板的速度閉環控制系統的控制效果取決于速度反饋增益Gv,即當Gv為0 時,結構主動阻尼為0,結構將做無衰減的震蕩;當Gv不為0 時,結構主動阻尼不為0,結構的震蕩逐漸衰減;隨著Gv增大,結構主動阻尼增大,震蕩衰減速度變快,從而實現了對無阻尼壓電功能梯度結構的振動主動控制.