曲面邊界黏性繞流的湍流模型改進方法研究1)

唐 聃 戴紹仕,2) 谷慧群 Bassam A.Younis

* (哈爾濱工程大學船舶工程學院,哈爾濱 150001)

? (加利福尼亞大學戴維斯分校,美國加利福尼亞州戴維斯 95616)

引言

邊界層分離所致的非定常、多尺度渦流結構廣泛地存在于各類工程領域的湍流中[1-2],并影響著湍流的生成、耗散等過程,進而直接影響著具有復雜幾何邊界結構遭受的流體動力.盡管大渦模擬(large eddy simulation,LES)方法已經應用于各類工程領域中湍流的預測問題上,但隨時間的推移,其計算性能的某些缺陷仍然存在[3-6].

目前,廣泛應用的經典常系數Smagorinsky 模型(Smagorinsky model,SM)[7]假設渦黏系數與湍流中的與局部、過濾的應變率和長度比尺成比例.這種假設導致了渦黏系數的過度預測[8-9],特別是對于以多尺度旋渦運動為主的湍流更加明顯.在實際的應用研究中,眾多學者也發現了該模型在近壁區過度耗散的問題,以致它無法準確地捕捉從層流到湍流的轉捩過程[3,8,10].為彌補這些缺陷,一些學者開始研究SM 模型中標準亞格子模型(SGS)的修正方法.Cheng 等[11]引入了基于壁面距離的van Driest阻尼函數來修正渦黏系數,在靠近壁面處實現了亞格子應力的強制衰減.但是在實際應用中該模型對復雜邊界(尤其是大曲率邊界)流動的計算并不理想,且無法準確地預測雷諾應力[12-13].隨后,Nicoud等[14]基于速度梯度張量的平方修正了渦流黏度的漸近性,進而提出了壁面自適應渦黏模型(wall adapting local eddy viscosity model,WALE).該模型很好地改進了壁面邊界流的預測能力,但是對于高雷諾數時的流動和強渦流系統的預報,它過度耗散的行為仍然十分明顯[15-16].近些年,基于Germano恒等式[17]和Lilly 最小二乘法,具有動態模型系數的Smagorinsky 模型(dynamic Smagorinsky model,DSM)得以發展,這種方法理論上要求在流場均勻的情況下計算平均模型系數,但這種平均過程缺少物理上的合理解釋,二次過濾過程又顯著降低了計算效率,并且在不規則邊界處的計算還會出現錯誤[18-19],此外對渦流場的求解仍呈現出過度耗散的行為[16,20].為了解決過度耗散的問題,Hughes 等[21]又提出了變分多尺度模型(variational multiscale model,VMM)來區分旋渦運動的大尺度和小尺度.隨后,一個正則化的版本(regularized varitional model,RVM) 由Jeanmart 等[22]初步提出,試圖提高渦流場的預報精度,進而Bricteux 等[23]探究此方法對低Re數槽道流中水平壁面流的預測能力,發現此方法對復雜壁面近壁處漸近行為的預報并不正確[22-23].近期,為了克服過度耗散的問題,動態模型系數的方法引起了很多學者的關注.如Montecchia 等[24]的顯式代數亞格子比尺模型,Tellez-Alvarez 等[25]的拉格朗日動力學模型(LDM),Shukla 等[26]與Sircar 等[27]的動態k方程亞格子模型,這些模型都因引入了額外的方程和濾波運算[28],不僅對復雜壁面形狀黏性繞流的模擬效果產生了不利影響,而且還使計算效率顯著降低[29].

為了更準確地捕捉大曲率邊界的邊界層分離和多尺度旋渦發放等流動特征,本文以具有大曲率壁面、復雜物理性質和廣泛工程應用的圓柱為例,針對亞臨界雷諾數時圓柱黏性繞流的多尺度旋渦發放問題,采用正則化變分模型(RVM)與WALE 模型相結合的方法,推導濾波算子、建立改進的大渦模型(MWALE),并采用C++語言開發計算代碼,在此基礎上研究改進模型中濾波算子 (n) 對大曲率邊界、多尺度旋渦發放所致水動力問題的計算能力和預報精度.

1 數值計算方法

1.1 控制方程

假設流體流動是不可壓縮的,濾波后的連續性方程和Navier-Stokes (N-S)方程為

基于線性應力?應變關系的Smagorinsky 假設[7],用亞格子(SGS)模型來近似τij

1.2 WALE 模型的改進

式中,Cw是WALE 模型參數.

盡管WALE 模型改善了壁面附近的亞格子應力分布,但是對大規模分離流的模擬,仍然產生了渦黏系數過高和能量過度耗散的問題[24].

將正則化變分模型(RVM)與LES 方法相結合后,明顯地,波數范圍從 [0,kmax/2] 平滑地過渡到[kmax/2,kmax].通過對LES 速度場中的進行高通濾波(high-pass filtered,HPF)得到HPF 速度場中的(n),并將其應用到SM 模型中渦黏系數和亞格子應力的計算上,發現該模型對多尺度渦流運動的耗散問題有顯著的改善[25].采用LES 速度場的與低通濾波(low-pass filtered,LPF)速度場的之差求得

考慮在三維物理空間中,LPF 濾波場的速度記為(為濾波器,i=1,2,3).本文的濾波器使用的是僅依靠相鄰網格計算的緊湊型離散濾波器(stencil-3)[30-31].該濾波器是二階濾波器,經過調諧,其傳遞函數G在LES 速度場中的截斷波數(kh=π)處變為零.

以n=1 為例,在一維空間中,將G應用于函數f(x),濾波后的(x) 可表示為

式中,h是網格間距,δ2/4 是簡化運算符.hl和hr分別是非均勻網格左側和右側的間距.

擴展到三維空間,是通過3 個方向的顯式離散濾波器(=??)求得.n=1,2 時,LPF 速度場中速度的通式為

式中,I為單位算子;為不同方向的簡化運算符,如=(fi+1,j,k?2fi,j,k+fi?1,j,k)/fi,j,k.n是離散濾波器的濾波階數;n=1 表示二階濾波器算子,n=2 表示4 階濾波器算子.

將式(10) 代入式(6),得到HPF 場中改進的WALE 模型中的亞格子應力

用式(11)來封閉控制方程,進行數值求解.

1.3 程序實現和數值求解

基于上述建立的MWALE 模型,采用C++語言在OpenFOAM 開源平臺上進行程序編譯,實現了此程序的開發和數值求解.

程序主體在源文件(*.C)中執行,源文件調用的各種庫和基本類在頭文件(*.H)中聲明.在make文件夾中,我們指定了編譯源文件的存儲位置和頭文件的聲明位置.然后,通過“wmake”命令生成庫文件(*.so),用于動態調用.應用MWALE 模型對多尺度湍流模擬的過程中,需要求解的偏微分方程可以采用OpenFOAM 中的“類”進行表示.下面以標準的動量方程為例,描述如下

基于有限體積法,該方程的離散化形式可表示為

針對黏性均勻流繞過孤立圓柱的問題,在數值模擬中時間項離散采用隱式的、二階精度向后差分(backward)算法、空間項離散也采用二階精度算法.鑒于在湍流研究中文獻[32-35]已證明: 在網格分辨率相同時,對流項采用二階精度(或更高)的迎風算法、二階中心差分算法在平均和脈動的精度計算上無太大區別,都不會引起數值耗散,因此,本文對流項的離散采用線性迎風穩定輸運(linear-upwind stabilized transport,LUST)算法,它是75%線性和25%線性迎風的混合算法,以避免可能出現的短波振蕩問題[32-34].拉普拉斯項和梯度項的離散,分別采用高斯線性修正算法和高斯線性算法.代數方程的求解采用基于算子分裂的壓力隱式算法 (pressureimplicit with splitting of operators,PISO)進行迭代求解.數值計算流程如圖1 所示.

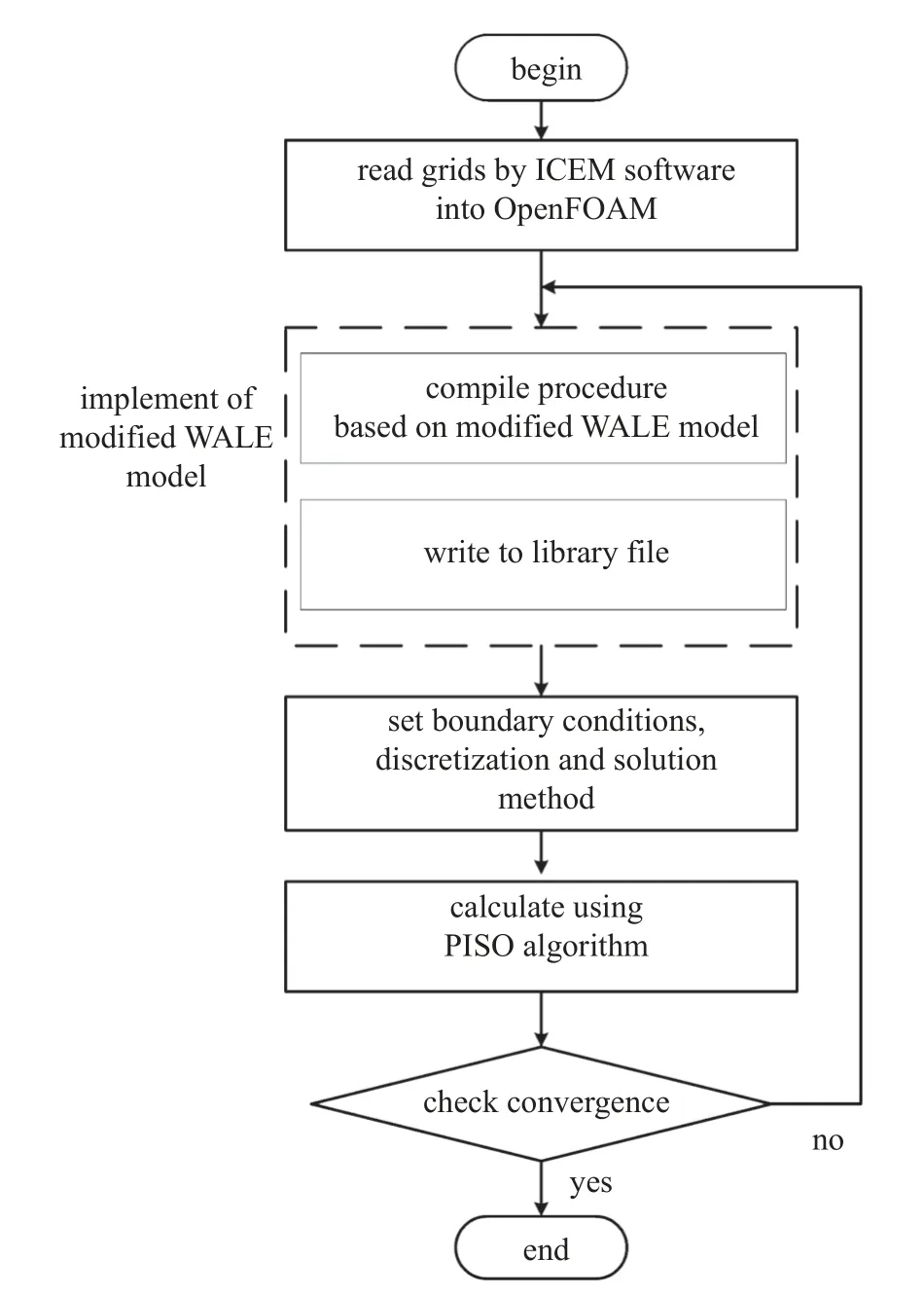
圖1 數值計算流程圖Fig.1 Basic chart of numerical calculation

2 網格設計

具有大曲率邊界的圓柱黏性繞流問題,流動中既有不固定的分離點,又有邊界層分離后的多尺度旋渦發放,旋渦發放形態和尾流運動隨時空都有很大的變化,流動現象非常復雜,實驗資料也很豐富.考慮到Re=4×104時尾流場中有關脈動特性的實驗和數值資料尤為豐富,所以本文選擇黏性流繞過圓柱的流動作為曲面邊界黏性繞流的典型代表,針對Re=4×104時圓柱流動分離所致的旋渦發放問題,采用上述建立的MWALE 模型及其數值求解方法開展數值模擬和分析.在笛卡爾坐標系中,計算域示意圖見圖2.圓柱底面的圓心位于(0,0,0)處,計算域的流向(x)、橫向(y)和展向(z)的尺度為29D×16D×πD,圓心距離計算域進口和出口的距離分別為9D和20D,距離側面的距離為8D.

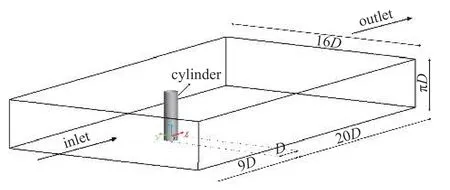
圖2 計算域示意圖Fig.2 Diagram of computational domain

為了更好地匹配圓柱體的曲面形狀,采用ANSYSICEM 軟件中的O-Block 技術進行拓撲映射,應用六面體網格進行計算域的空間離散(見圖3).為滿足大渦模擬的離散質量要求,網格增長率采用1.05.針對圓柱體近壁區的第一層網格(y+),本文設計了3 種方案:y+分別為5,2.5 和1.依據網格近密遠疏的設計原則,沿柱體徑向相應地布置95,115 和141 個種子;沿柱體周向和展向分別布置4×100 和11 個種子.對應3 種設計方案的網格定義為: 粗網格(M1)、中網格(M2)和細網格(M3),離散單元總數見表1.

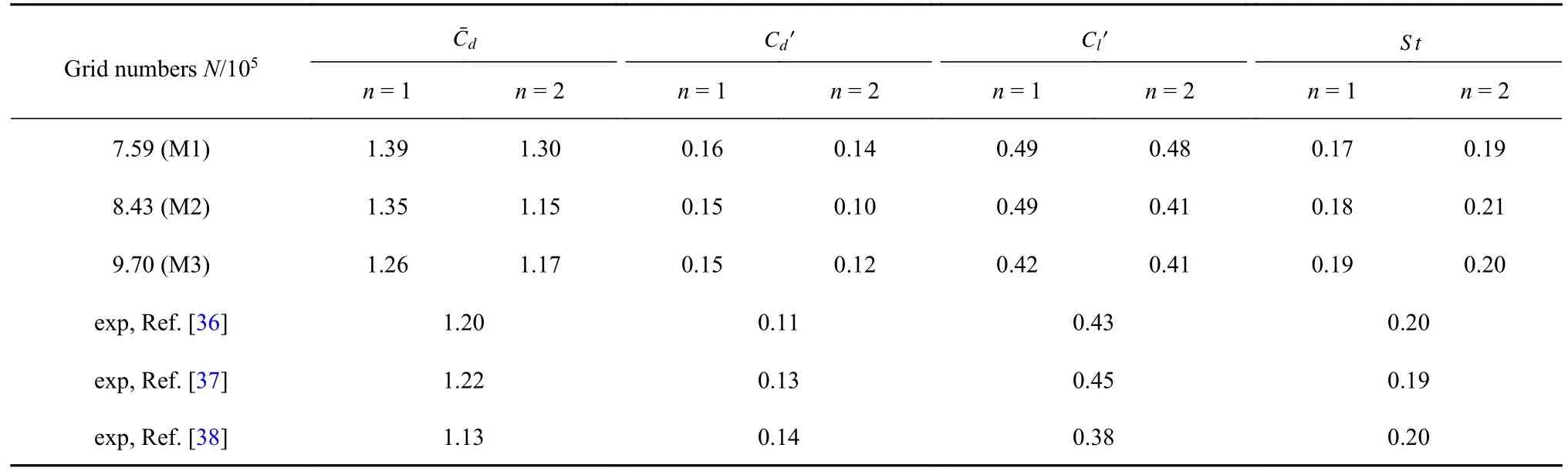
表1 圓柱水動力系數對比表Table 1 Comparisons of hydrodynamic coefficients of the cylinder

圖3 流場計算域的網格分布和邊界條件示意圖Fig.3 Diagram of grid distribution and boundary conditions in the computational domain

計算域的邊界條件和初始條件如圖3 所示.進口邊界采用狄利克雷條件,即u=U;出口邊界采用黎曼條件,即 ?u/?n=0.圓柱體壁面采用無滑移邊界條件.計算域的兩側和上下邊界均采用無窮遠邊界條件.為保證計算收斂,時間步長(Δt)滿足庫朗數C=U·Δt/Δx≤1 (Δx為網格間隔),Δt取5×10?3s.

表2 給出了3 種網格設計方案(M1,M2 和M3),n=1,2 時MWALE 模型預報的水動力系數對比.由表可見,n=1 時采用M1 和M2 預報的結果差別很小,但與Bouak 等[36]、West 等[37]和Schewe 等[38]實驗測試的結果相比偏離很大,尤其是和的預報誤差大于10%,然而采用M3 預報的,,和S t分別為1.26,0.15,0.42 和0.19,與實驗結果[36-38]相比誤差都小于10%,明顯更吻合.n=2 時,3 種網格方案預報的結果與實驗結果更接近.與n=1相比,顯然M3 網格的預報精度更高.這些充足的證據證明了第3 種網格設計方案(M3)具有更好數值計算精度,因此后續開展的一系列研究都采用M3方案.

3 結果討論與分析

為了獲悉MWALE 模型對曲面結構黏性繞流問題的計算能力,本文以圓柱為代表,詳盡地研究了MWALE 模型中兩種濾波算子(n=1,2)對圓柱黏性繞流多尺度旋渦發放的流動特性和力學特性的預報精度的影響.

圓柱體的近壁尾流區是旋渦生成和發展的重要區域.在此區域中,渦量和速度的分布特性直接影響圓柱體的受力特性.圖4 首先給出了基于兩種濾波算子(n=1,2)的MWALE 模型所預測的平均渦量(＜?＞)沿圓柱體表面分布的對比.由圖可見,在圓柱體迎流區(0°≤θ ≤90°)內,兩種算子預測的平均渦量都隨 θ 的增加先增大后減小,在 θ=45°時都捕捉到了渦量的峰值;并且預測的平均渦量分布與Son 等[39]的實驗測試結果吻合得都很好,但是WALE模型預測結果明顯大于實驗值.在圓柱體的背壓區(90°＜θ ≤180°),也是多尺度旋渦發放的區域,WALE模型和n=1 的MWALE 模型所預測的平均渦量都出現顯著的波動,且預測的渦量明顯偏大,而n=2的MWALE 模型預測的平均渦量卻非常平穩,且與實驗結果[39]吻合得很好.

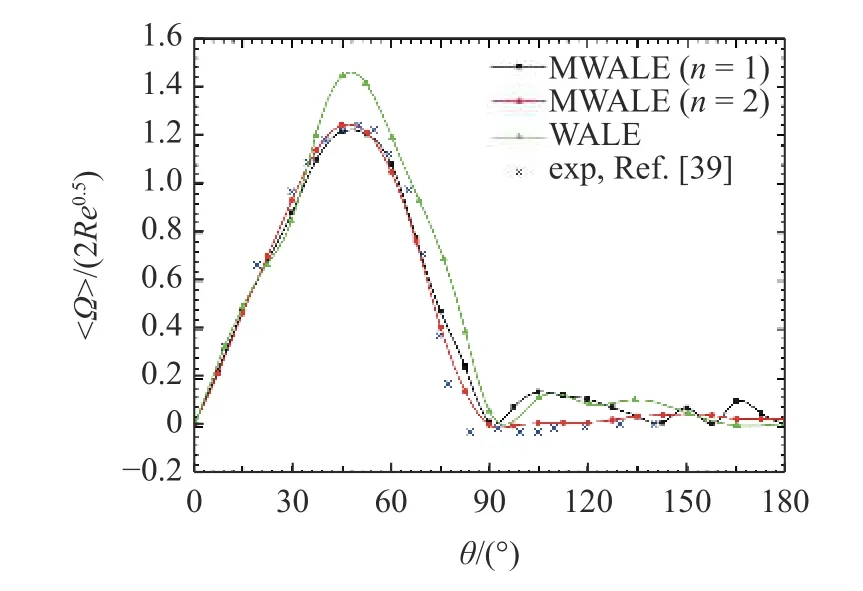
圖4 圓柱表面上平均渦量分布的對比Fig.4 Distributions of mean vorticity on the cylinder surface

圖5 進一步給出了MWALE 模型中兩種濾波算子所預測的一個旋渦脫落周期內、典型時刻渦量等值面的分布和SGS 渦黏系數分布云圖.由圖5(a)可以明顯地看出,圓柱壁面發生流動分離后形成了多尺度的旋渦結構,在隨主流下泄的過程中發放的旋渦結構都出現了破碎現象,但與WALE 模型和n=1 的MWLAE 模型相比,n=2 的MWALE 模型預測的尾流渦量波動和破碎現象明顯地減弱,并且圓柱壁面上渦量的分布也更均勻、更光滑,遠離圓柱壁面區的渦量耗散也明顯減小.由圖5(b)給出在不同相位時SGS 渦黏系數分布云圖的對比,顯然可見,3 種計算模型中預測的 νSGS都呈現擴散現象,但是WALE 模型預測的 νSGS明顯最大,并且在擴散中耗散現象最嚴重(尤其在尾流區).相比之下,n=1的MWALE 模型預測的 νSGS有所降低,耗散現象也有所削弱;而n=2 的MWALE 模型預測的 νSGS擴散性明顯最小,黏性耗散也最輕.這說明n=2 的濾波算子更好地改善了WALE 模型對SGS 渦黏系數預測過高和耗散過大的問題.這也正好解釋并揭示了下文中旋渦流的脈動特性和雷諾應力偏大的實質內因.

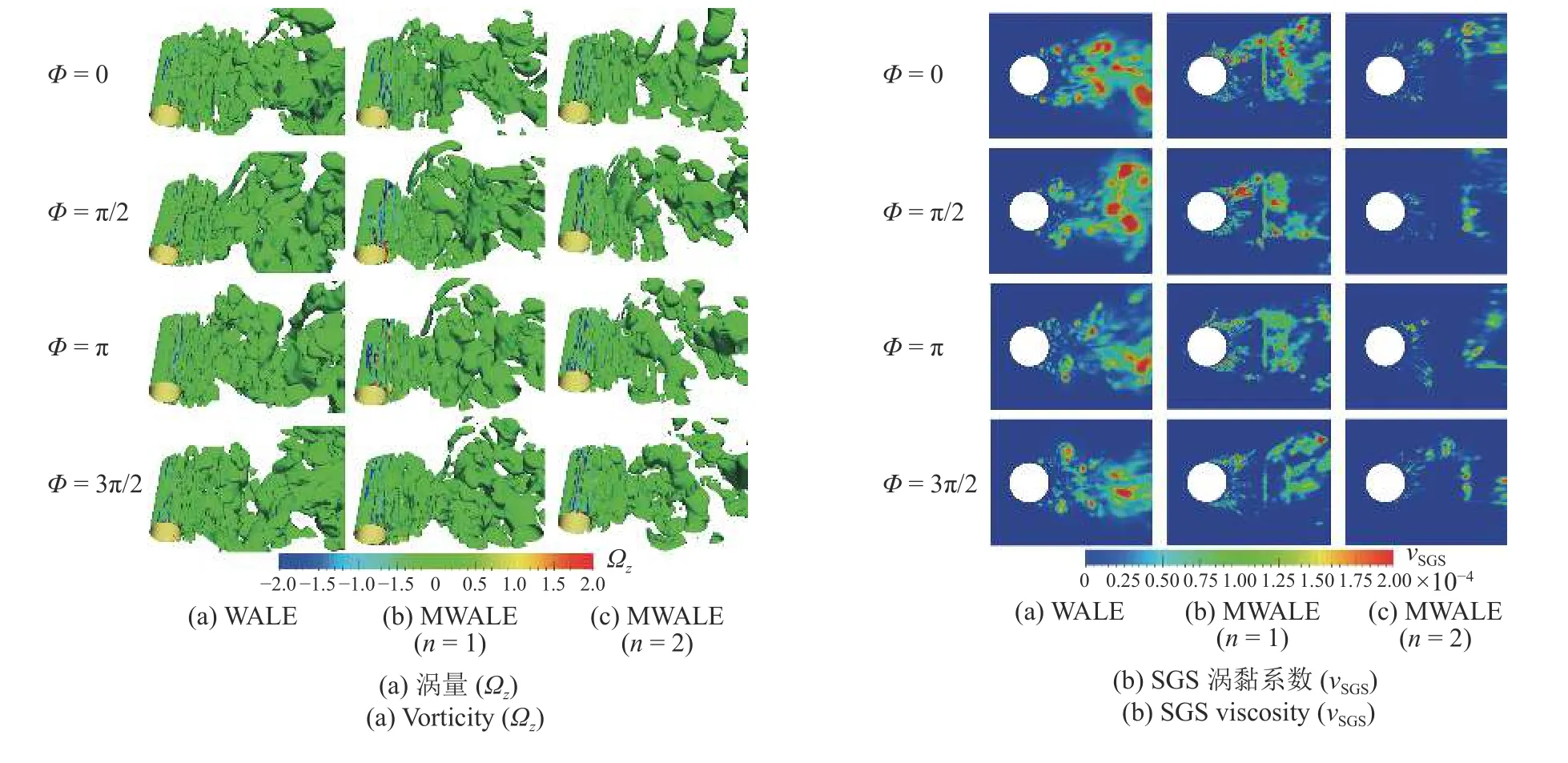
圖5 圓柱尾流渦量等值面和圓柱中截面SGS 渦黏系數云圖分布Fig.5 Distributions of vorticity isosurfaces in the wake of the cylinder and SGS viscosity contour in the middle section of the cylinder

邊界層發生分離后,在圓柱背壓區附近的旋渦運動得以發展,會出現明顯的回流現象,此區定義為回流區.回流區長度與再循環旋渦長度(Lr,為沿尾流中心線從圓心到平均流向速度符號變化處的距離)相等.由于回流區內流體的剪切應力較大,并且剪切力與平均流的相互作用非常強烈,從而多尺度旋渦在此生成、發展,形成湍流.回流區的長度被認為是評估圓柱繞流特性的重要指標之一.為了評估MWALE 模型中兩種濾波算子對回流區內回流的捕捉能力和時間平均的回流區長度的預測精度,圖6 給出了沿圓柱尾流中心線(y/D=0)流向無量綱平均速度分布的對比.由圖可見: WALE 和MWALE模型預測的＜＞/U速度形線在 0.5 ≤x/D≤1.5 都成拋物線形分布,且＜＞/U都出現負值.MWALE 模型(n=1,2) 預測的Lr/D(用D無量綱) 分別為1.31 和1.40,與Unal 等[40]實驗測試(Re=4.13×104)的結果1.45 相比,n=2 預測的誤差僅為3.5%,顯然誤差更小;與WALE 模型和DTKE 模型[41]的預測值1.33 和1.13 相比,n=2 的MWALE 模型預測的精度明顯更高.關于回流區內的速度形線,相比于n=1 的WALE 模型和DTKE 模型的預測結果[41],n=2 的MWALE 模型與實驗測試結果[40]吻合的更好,尤其是預測的＜＞/U最小值(?0.28)與實驗值(?0.26)非常接近.流過回流區后,因旋渦發放下泄速度的增大,＜＞/U隨x/D＞1.5 增大而增大,并逐漸逼近來流速度(U),顯然,n=2 的預測＜＞/U隨x/D分布與實驗結果吻合得更好.

圖6 沿尾流中線的平均流向速度Fig.6 Mean stream-wise velocity along the wake centerline

圖7 又進一步給出了兩種算子預測的在尾流中心線上流向和橫向脈動速度(＜＞/U2,＜＞/U2)沿流向的分布.由圖7(a)可見,在近壁尾流區(0.5 ≤x/D≤2.5),MWALE 模型和WALE 模型所預測的＜＞/U2都隨x/D的增加先迅速增加,后迅速降低,并且都在x/D=1.1 處出現峰值,相應的峰值分別為0.165,0.132 和0.222.與Szepessy 等[42]、Lim 等[43]和Unal 等[44]的實驗值(0.125～0.142)相比,顯然基于n=1 的MWALE 和WALE模型預測的值都明顯偏大,而n=2 的預測值在實驗值范圍內;在尾流遠場區(x/D≥2.5),因不同尺度旋渦的充分發展,隨x/D的增加＜＞/U2的變化逐漸趨于平緩,兩個算子預測的＜＞/U2線形也逐漸趨于一致,并且與Lim 等[43]實驗值十分接近,相比之下,WALE 模型的預測值明顯小于實驗值.圖7(b)又給出兩種算子預測的橫向脈動速度(＜＞/U2)沿流向的分布.明顯地可以看出: 兩種算子預測的＜＞/U2峰值都出現在x/D=1.3 附近,但是n=1 的MWALE 模型和WALE 模型所預測的＜＞/U2峰值都遠大于Unal 等[44]的實驗值,并且它們所預測的＜＞/U2分布線形明顯地偏離了實驗測試曲線;而n=2 預測的＜＞/U2峰值(0.46)與實驗值[44](0.47)吻合得更好.此外,n=2 預測的＜＞/U2分布的線形也與實驗測試結果更一致.由此可見,n=2的濾波算子對WALE 模型的改進效果更好,對渦流場中脈動速度的預測能力更好,能夠更準確地捕捉曲面邊界發放的多尺度旋渦結構引起的流體脈動特性.

為進一步評估MWALE 中濾波算子的階數對尾流場中速度分布預測能力的影響,截取約40 個旋渦脫落周期(t*=200～400,t*=Ut/D))進行數據分析.圖8 給出了4 個典型剖面(x/D=0.6,1.5,2.0,2.5)處無量綱平均速度分量(＜＞/U,＜＞/U) 的橫向分布.由圖8(a)可見: 在x/D=0.6 時,MWALE 模型(n=1,2)和WALE 模型預測的＜＞/U沿尾流中心線都呈現橫向放置的“U”形分布,雖然與Unal 等[40]的實驗形線和DTKE 模型預測的行線[45]都很吻合,但是WALE 模型預測的結果在尾流中線附近出現明顯的波動;隨x/D的增加,3 種模型(MWALE,WALE 和DTKE[45])預測的＜＞/U的形線都由倒向的“U”形變為倒向的“V”形分布,并且速度變化幅度都逐漸減小,與實驗測試[40]的趨勢符合的也很好(見圖8(b)～圖8(d)).盡管n=1 預測的＜＞/U的最小值略大,但是WALE 模型和濾波算子對＜＞/U預測的差異可以忽略.可見,3 種模型對＜＞/U的預測能力相當.從圖8(a)～圖8(d)中＜＞/U分布可見: 兩種濾波算子和WALE 模型預測的尾流中心線上的橫向速度都呈現反對稱分布,但與WALE 模型、DTKE 模型[45]預測結果相比,基于兩種濾波算子的MWALE 模型預報的＜＞/U分布與實驗結果[40]吻合的更好;隨x/D的增加,因多尺度旋渦的充分發展,＜＞/U變化梯度明顯增大,與實驗測試結果[40]相比,n=2 的MWALE 模型預測的誤差明顯最小(見圖8(a)～圖8(d)),這說明n=1 的濾波算子對WALE模型耗散問題的改進不佳,導所預測的多尺度旋渦發展中的耗散性偏大.這些證據再次說明n=2 的MWALE 模型預測尾流平均速度的能力相對更好.

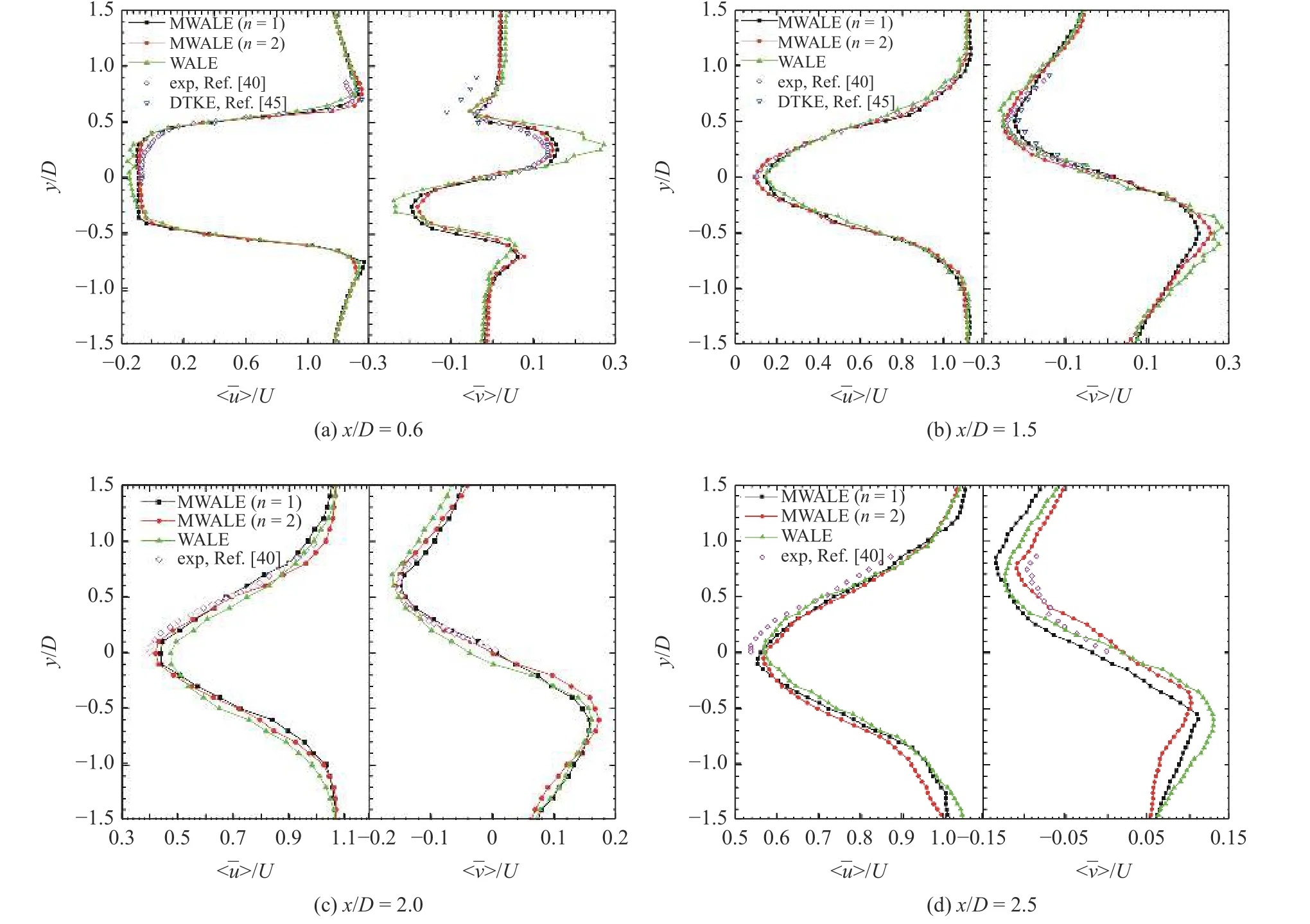
圖8 尾流不同位置處平均速度分量的分布Fig.8 Distribution of mean velocity component at different locations in the wake

圓柱黏性繞流因邊界層分離發生的多尺度渦流的脈動特性,至今鮮有關于大渦模擬模型對其預測性能評估的詳細報道(尤其是Re≥4.0×104).為了進一步評估MWALE 模型對多尺度旋渦所致雷諾應力分布的計算能力,針對Re=4.0×104時圓柱繞流旋渦發放所致雷諾應力分布預測能力問題,本文進一步討論Re=4.0×104時MWALE 模型所預測的圓柱近壁處雷諾應力分布.圖9 給出了MWALE 模型(n=1,2)和WALE 模型預測的穩態時、流向和橫向雷諾應力分布云圖的對比.由圖9(a)可見,流向雷諾應力(＜＞/U2)沿尾流中心線都呈現對稱的漿片狀分布,并都有明顯的鞍點特征,但是n=1 的MWALE模型和WALE 模型預測的最大＜＞/U2范圍明顯比實驗結果[44](Re=4.13×104)大,而n=2 預測的與實驗結果十分接近;實驗測得的橫向雷諾應力(＜＞/U2)沿尾流中心線的分布呈現對稱的橢圓狀[44](見圖9(b)).顯然,WALE 模型和n=1 的MWALE 模型過度地預測了＜＞/U2值,使得圓柱背壓區處＜＞/U2值明顯偏大,并且尾流區＜＞/U2的分布形狀也由橢圓變成了近似的矩形.然而,n=2 預測的＜＞/U2分布與文獻[44]的測試結果十分相近.

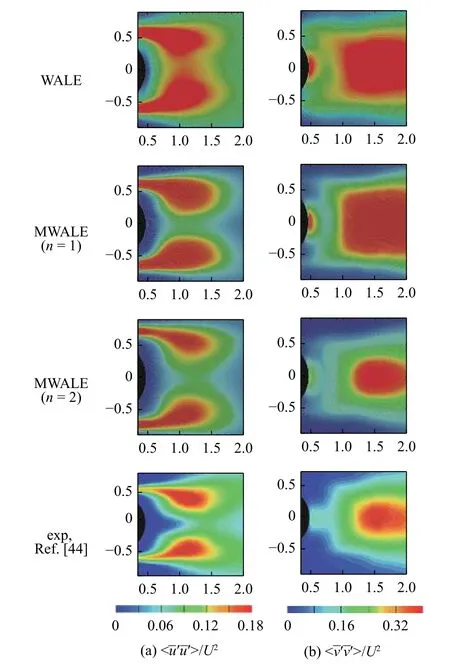
圖9 圓柱尾流雷諾應力云圖對比(Re=4.0×104)Fig.9 Comparisons of contour of the fluctuating velocity component in the wake (Re=4.0×104)

為了定量的評估濾波算子對雷諾應力預測精度的影響,圖10 又給出了Re=3.9×103時在圓柱尾流兩個典型位置處的雷諾應力分量(＜＞/U2,＜＞/U2)分布的對比.在x/D=1.06 時,與Lourenco等[46]的實驗結果相比,MWALE 模型、WALE 模型和DTKE 模型[47]預測雷諾應力分布趨勢與實驗測試的趨勢一致,但是在近尾流中心線上WALE 模型和n=1 的MWALE 模型預測的雷諾應力橫向(y/D)分布都明顯偏大(見圖10(a)～圖10(b)),WALE 模型尤為明顯,而DTKE 模型[47]預測的流向和橫向雷諾應力又非常小,幾乎為0.隨著旋渦運動順流的發展,沿流向x/D=2.02,1D尾流寬度范圍內,與實驗值相比,DTKE 模型[47]和n=1 的MWALE 模型預測的＜＞/U2峰值都明顯比實驗值大,WALE 模型的預測值又略小,而n=2 測預測的＜＞/U2分布和峰值都與實驗測試[46]結果非常吻合.對于＜＞/U2的預測,WALE 模型和DTKE 模型的預測值明顯小于實驗值,而基于n=1 的MWALE 模型預測的又明顯偏大,但是n=2 預測的＜＞/U2分布與實驗結果很好地吻合在一起.n=2 的MWALE模型對雷諾應力良好的預測,進一步充分地證明了n=2 的MWALE 模型對多尺度渦流脈動特性的預測具有更高精度.

在多尺度渦流的作用下,圓柱體會受到升、阻力.濾波算子對圓柱體的無量綱壓力(中截面處)、升力和阻力的預報精度影響見圖11～圖12.由圖11(a)可見,n=2 的MWALE 模型預測的穩態壓力系數(Cp)周向(θ)分布與實驗結果[48-50]吻合地很好,而n=1 的MAWLE 模型和WALE 模型預測的Cp值明顯小于實驗結果[48-50];對于脈動壓力系數()周向的預測見圖11(b).顯然,當 θ＜60°時,n=1 或2 預測的值都與實驗值[37](Re=4.0×104) 相吻合,但是WALE 模型的預測結果卻略大;當θ＞60°時,n=2 預測的值也與實驗值吻合的非常好,但是n=1 和WALE 模型預測的值波動較大,且大于實驗值[37],WALE 模型預測值偏大更顯著,這是因耗散偏大所致.

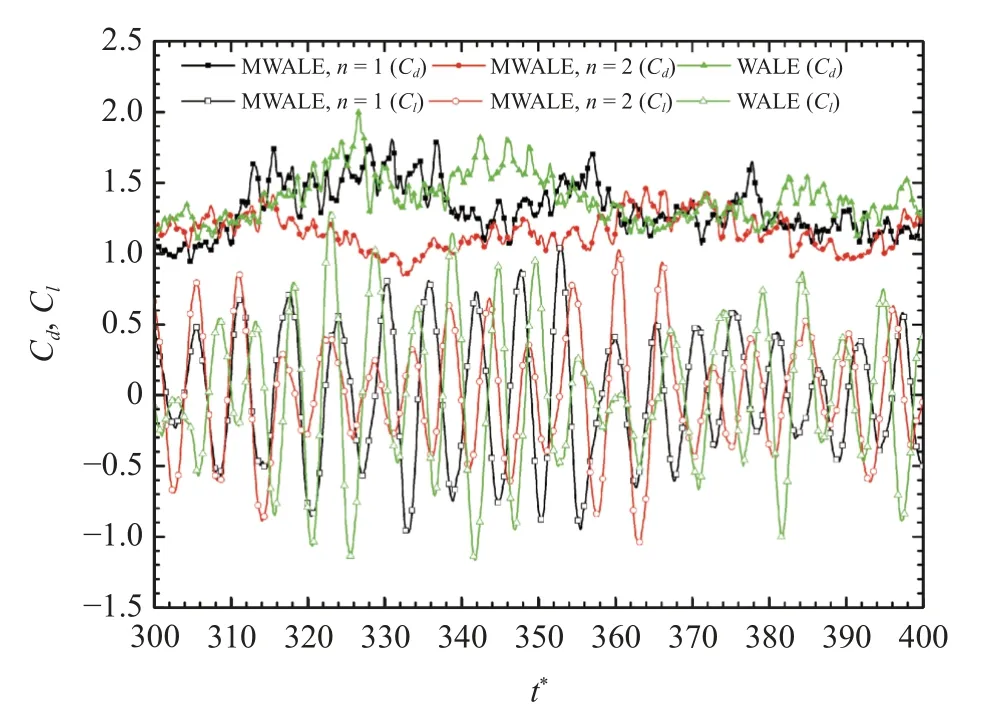
圖12 圓柱的升力和阻力系數時歷曲線Fig.12 Time histories of lift and drag coefficients

圖12 給出了兩種濾波算子預報的無量綱升、阻力(Cl,Cd)的時歷曲線.由圖可見,WALE 模型和n=1 的MWALE 模型預測的Cd值波動都很大.兩種模型預測的穩態和脈動阻力系數(和)分別為(1.35,0.16)和(1.26,0.15),與文獻[36-38]的實驗結果(1.13～1.22,0.11～0.14)相比都偏大,但是n=2預報的和為1.17 和0.12,都在實驗結果范圍內;對于升力,WALE 模型預測的值為0.49,而MWALE 模型(n=1,2)預測的值分別為0.42,041,都在實驗[36-38]范圍內(0.38～0.45).因此,整體來看,n=2 的MWALE 模型對圓柱遭受的渦激勵力的預報精度更高.

4 結論

針對曲面邊界結構因邊界層分離所致的非定常、多尺度渦流的大渦模擬過度耗散問題,本文采用正則化變分模型(RVM)與WALE 模型相結合的方法,獲得了改進的大渦模型(MWALE),開發了數值計算程序.在此基礎上,以經典的圓柱繞流作為曲面邊界黏性繞流的代表,研究了MWALE 模型中濾波算子(n=1,2)對亞臨界雷諾數時圓柱黏性繞流的瞬時、多尺度渦流的流動特性和力學特性預測能力的影響.研究得出以下主要結論.

(1)改進的WALE 模型采用4 階濾波算子(n=2)能更好地反映出圓柱壁面處平均渦量及尾流中瞬時渦量分布特性,對圓柱體背壓區處再循環旋渦長度(Lr)的預測也更準確.

(2)與WALE 模型、DTKE 模型和二階濾波算子(n=1)的MWALE 模型相比,4 階濾波算子(n=2)的MWALE 模型能更準確地預測圓柱黏性繞流尾流的流向、橫向脈動速度的分布特性和雷諾應力的分布特性.

(3) 在圓柱體背壓區,穩態壓力和脈動壓力對MWALE 模型中濾波算子階數很敏感.因為4 階濾波算子很好地解決了WALE 模型過渡耗散問題,所以它對多尺度旋渦發放所致的脈動壓力及升、阻力的預測精度更高.