顆粒材料破碎行為數值分析方法研究綜述1)

梁紹敏 馮云田 趙婷婷 王志華

* (太原理工大學機械與運載工程學院,太原 030024)

? (斯旺西大學辛克維奇計算工程中心,英國斯旺西 SA1 8EP)

引言

顆粒材料在自然界和工程領域普遍存在,如谷物、砂石和土壤等.在水利、港口和交通等工程領域中,堆石、砂石和砂土等顆粒材料得到了廣泛應用,在堤壩、隧道和地基等工程中,大載荷作用下顆粒材料容易發生破碎現象,且顆粒材料的破碎行為會給工程和建筑建設帶來極大的影響,如三峽水利樞紐工程中的填筑材料,其破碎率可能會達20%.因此,顆粒材料的破碎行為已經引起人們的關注,并且逐漸成為顆粒材料力學性質研究的新課題[1].此外,顆粒的破碎行為會引起顆粒系統級配的改變,從而影響其物理力學性質,大顆粒破碎后產生的小顆粒填充到顆粒系統孔隙中也會導致系統孔隙減小從而引起變形[2].同時,分析細觀尺度下顆粒的破碎現象與宏觀尺度下材料的非線性行為之間的關系,對顆粒破碎的宏、細觀機理揭示具有重要意義[3].由此看來分析顆粒破碎過程既有實際的工程意義,又有理論的研究價值.

顆粒破碎是指顆粒材料在外載荷作用下發生開裂、崩解或磨耗,從而導致級配改變的現象,且受加載方式、外載荷大小以及顆粒形狀、尺寸、自身強度等影響[4].顆粒材料的破碎行為會導致顆粒形狀、尺寸、強度、配位數、級配以及密實度等發生變化,甚至引起顆粒系統運動狀態的變化.顆粒的破碎過程存在以下3 個特征狀態: 起始狀態、臨界狀態和終止狀態.把顆粒開始涉及破碎的初始狀態定義為起始狀態,一般破碎的起始狀態可人為地合理指定,所以具有相對性;顆粒材料的應力和應變不再變化,而偏應變繼續發生變化的狀態稱為臨界狀態,臨界狀態是客觀的;當顆粒材料內部不再有破碎現象發生的極端狀態稱為終止狀態,所以終止狀態具有唯一性.顆粒破碎具有不可逆性、累加性、應力路徑相關性和卸載不產生顆粒破碎的特點[4].

目前,對顆粒破碎的研究主要采用試驗的方法,研究內容主要有破碎現象的描述、評價指標的建立、破碎影響因素分析以及破碎對顆粒力學特性的影響等內容.國內外已經開展了大量針對顆粒破碎的試驗研究[5-6],并取得了一定的成果,如建立了顆粒破碎的評價指標,討論了影響顆粒破碎的因素,并在試驗結果的基礎上建立了顆粒彈塑性本構模型[7].典型的工作有通過改變級配、相對密度、圍壓等條件對顆粒材料進行大型三軸剪切試驗,分析其強度、變形及剪脹特性[8].

顆粒破碎過程是一個長期的、漸進的過程,而實驗室試驗僅僅可以模擬導致顆粒破碎的自然條件或漫長加載歷史中的某一階段[9],無法完全還原自然界中真實顆粒的破碎過程.此外,由于試驗過程中無法滿足試驗材料和作用載荷的同一性,因此難以保證多次試驗初始條件的一致性,導致結果的重復性較低,這樣獲得的研究結果對研究真實破碎過程意義不大.即使可以保證起始應力狀態的一致性,不同加載歷史或路徑也將導致顆粒破碎后的大小以及破碎過程的能量變化不同.此外,試驗研究還有成本高、耗時費力、難以揭示破碎的細觀機理并存在一定的危險性等缺點.數值方法的快速發展和計算機技術的飛速提高,使得通過數值方法研究顆粒破碎成為可能.與實驗室試驗相比,數值模擬更容易獲得物理參數或現象,如裂紋的萌生、擴展等,因此,數值模擬方法得到發展和推廣.當然,實驗室試驗對驗證理論和數值方法的有效性和準確性方面發揮了很重要的作用.

本文首先整理了目前研究顆粒破碎使用較多的數值分析方法,包括黏結?破碎法、碎片替代法、比例邊界有限元法、組合有限元?離散元法和近場動力學法,包括方法的提出、發展、實現過程以及方法的優勢和存在的問題.然后從目前的主要研究成果著手,詳細講述了破碎過程的細觀機理研究和顆粒材料破碎在工程中的應用.最后對目前有關顆粒破碎的研究進行總結,并對未來的發展趨勢進行展望.

1 基于離散元法的顆粒破碎數值算法

采用數值方法研究顆粒破碎過程時,考慮顆粒的離散特性,基于離散元方法理論則是最為合理和有效的方法.這一節將主要介紹基于離散元方法原理的黏結?破碎法和碎片替代法.

1.1 黏結?破碎法

1.1.1 黏結?破碎法的提出與發展

2000年Robertson[10]首次提出顆粒的黏結模型(bonded particle model,BPM),詳細介紹了如何將單顆粒黏結成組合顆粒.2004 年Potyondy 等[11]對黏結顆粒通過二維和三維離散元軟件PFC 對巖石的破碎過程進行了仿真,隨后該方法被應用于脆性顆粒材料破碎過程的研究中.黏結?破碎模型將一定數量的基礎顆粒通過黏結鍵形成顆粒簇,當基礎顆粒間的黏結作用失效時,顆粒發生破碎行為.

黏結?破碎法在一定程度上推進了顆粒破碎的研究,并在巖土工程中解決了一些問題.如基于黏結?破碎法,構建土壤的顆粒簇,并通過壓縮試驗研究了顆粒材料破碎對土壤臨界狀態的影響[12];構造砂土的顆粒簇,對砂土顆粒在高應力下的破碎效應進行模擬,通過改變顆粒的細觀參數、外載荷的加載速率、顆粒簇的數量以及黏結顆粒的平均粒徑等分析了破碎現象的影響因素[13];構造堆石料的顆粒簇,通過雙軸剪切數值試驗,再次肯定了該方法模擬真實顆粒材料破碎特性的有效性[14];構造不規則形狀的堆石顆粒簇,用以模擬堆石顆粒在破碎過程中的尺寸效應[15];采用球形單元黏結成不規則的碎石料顆粒簇,改變應力加載路徑分析顆粒材料破碎對碎石料應力–應變關系及體應變特性的影響,再次證明了離散元方法能夠較為準確地獲得碎石顆粒的力學特征[16].Lu 等[17-18]采用不可破碎的“超級顆粒”構造真實形態顆粒,將一定數量的顆粒與“超級顆粒”通過平行黏結鍵連接,通過判斷平行黏結失效與否來確定小顆粒與“超級顆粒”的合離,從而實現顆粒破碎過程模擬,并將其用于對道砟顆粒棱角斷裂過程的分析,破碎過程如圖1 所示.以上研究再現了顆粒材料破碎現象,對顆粒破碎過程的認識有一定的推動作用.

圖1 黏結顆粒構造示意圖[17-18]Fig.1 Schematic diagram of bonded particles[17-18]

以上研究主要是采用球體作為基礎單元通過黏結鍵構造顆粒簇,為了更接近真實顆粒形態,以正四面體為核通過晶胞繁衍的方法生成堆石顆粒,對三軸剪切作用下堆石料的破碎過程進行研究[19].針對復雜顆粒形狀,湘潭大學龍志林團隊[20]采用凸多面體塊作為基本顆粒,通過可逆函數法對顆粒破碎強度變異性進行建模,如圖2 所示.此外,采用傳統的修正“巴西”準則作為破碎準則,再根據顆粒的接觸點和質心可以確定顆粒內部最終斷裂,一旦目標顆粒滿足斷裂準則,它就會被一系列與最終斷裂相一致的虛擬切割面切割成多個碎片.這樣可以避免局部應力的產生及質量和體積的不守恒.這種方法不必預定義碎片的模式[20-23].該研究將黏結基礎單元由球體發展到多面體,這使黏結顆粒的幾何形狀與真實顆粒更加接近.

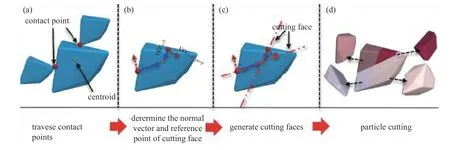
圖2 破碎過程的實現[20]Fig.2 Realization of breakage process[20]

目前國內外已經發展了多種離散元模擬軟件,其中采用黏結?破碎法實現顆粒的破碎分析的主要有PFC、大連理工大學季順迎課題組研發的SDEM、南京大學劉春課題組的MatDEM 等.在處理多顆粒破碎問題時,EDEM 也是基于黏結?破碎模型實現的.

1.1.2 黏結?破碎法對顆粒破碎細觀力學機理的研究

Griffith 強度理論認為固體材料中包含眾多細小裂紋,在外力作用下這些裂紋的尖端會出現應力集中現象,且這個應力始終為拉應力,稱之為誘導應力,當這個應力大于材料的抗拉強度時,尖端的裂紋將發生擴展并導致材料最終的破壞[3],這就是材料破碎機理研究的起源.借鑒材料的破壞機理研究方法,考慮顆粒材料的破碎機理,需要討論破碎產生的原因,包括引起破碎的外因、內因,破碎發生的初始狀態、發展過程以及最終的狀態.同時,要對破碎進行描述和衡量,還需要提出合理的破碎指標[24].顆粒的破碎機理直接決定破碎準則的建立,對破碎過程的模擬具有決定性作用[25].

通過關注顆粒內部接觸力的變化情況以及破碎發生的位置,從而獲得顆粒破碎的演化規律,進而揭示顆粒破碎的細觀力學機理.Cil 等[26]采用數值方法記錄了黏結顆粒內裂紋的產生和擴展過程,并與X-ray 掃描結果進行對比,發現模擬結果與掃描結果基本一致,如圖3 所示,這在一定程度上將顆粒材料破碎的現象研究發展到破碎過程的機理研究.Wang等[27-28]研究了顆粒材料破碎與顆粒材料剪切破壞行為之間的關系,如圖4 所示,通過微觀力學分析和機理演示,深入研究了平面應變剪切條件下顆粒破碎對致密可壓試樣的應力比、體應變、塑性變形和剪切破壞行為的影響.首先,基于單個土壤顆粒真實斷裂行為對顆粒試樣進行建模,通過對比壓板壓縮模擬結果與物理實驗室試驗結果證明了模型的有效性,如圖5 所示;然后研究了影響顆粒材料破碎的主要因素,結果表明,體積膨脹率和峰值應力比、塑性變形機制和剪切破壞模式隨土壤可壓性的變化是影響顆粒材料破碎的主要因素;最后,對破碎的機理進行了討論,從宏觀和微觀力學現象出發,提出剪切帶和大規模體積收縮是致密試樣的兩種端部破壞模式,且這兩種模式分別由顆粒重排引起的膨脹和顆粒材料破碎引起的壓縮控制,在土壤可壓性和圍壓的中等范圍內,兩種破壞模式是組合和競爭關系,如圖6 所示[27].

圖3 單顆粒、三顆粒柱的SMT 和DEM 圖像以及不同載荷水平下實驗室規模的壓縮試驗[26]Fig.3 SMT and DEM images of single-particle and three-particle columns as well as laboratory-scale compression tests under different load levels[26]

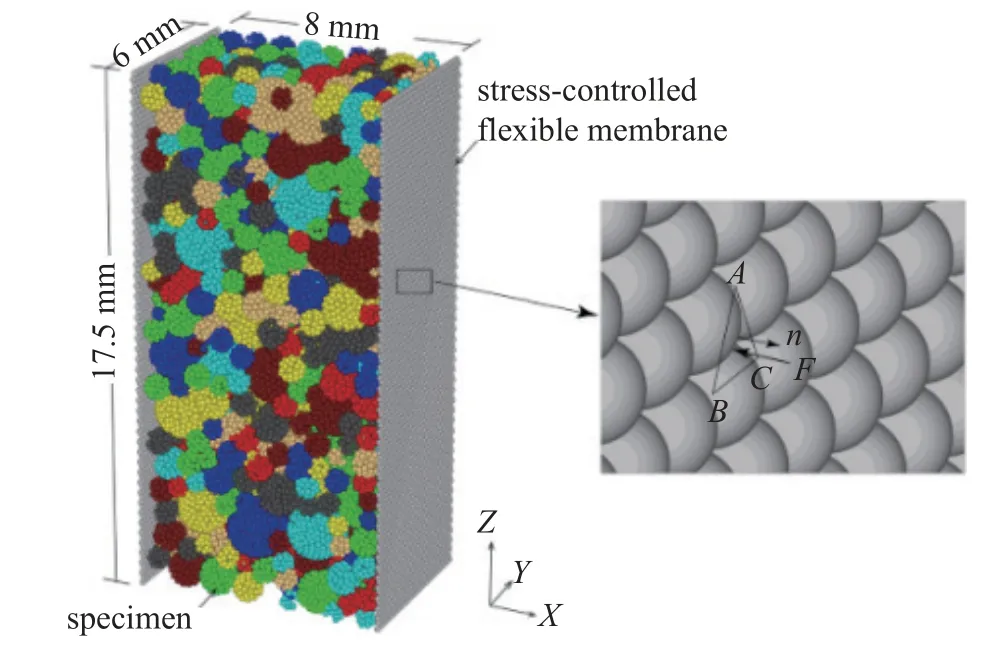
圖4 具有膜型柔性側邊界的DEM 試件[27]Fig.4 DEM specimens with membrane-type flexible side boundaries[27]

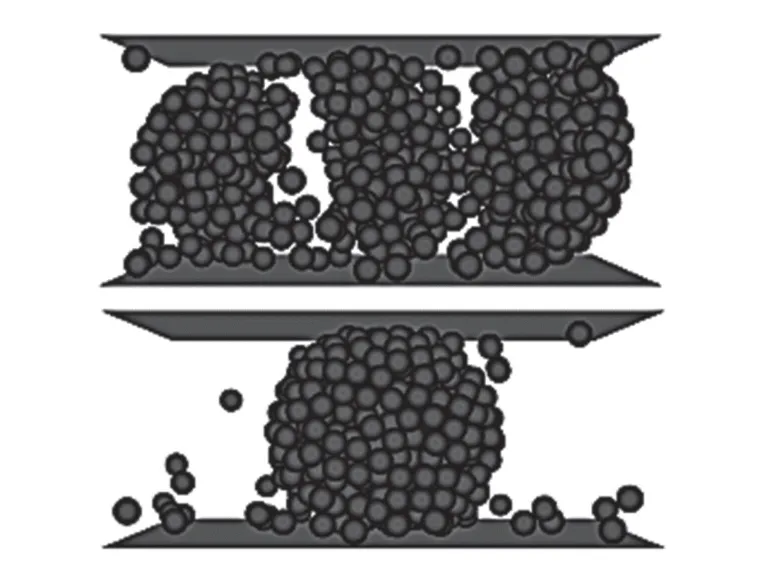
圖5 單顆粒壓裂典型模擬結果[27]Fig.5 Typical simulation results of single particle fracturing[27]

圖6 黏結單元及其在20%軸向應變下的顆粒位移和旋轉場[27]Fig.6 Bonding element and particle displacement and rotation field under 20% axial strain[27]

Wang 等[29]建立了水泥的橢球顆粒模型,采用黏結?破碎法分析了單顆粒的破碎機理,如圖7 所示.研究結果表明,高強度粒子碎裂成幾片,而低強度粒子碎裂成兩大塊.這說明顆粒的斷裂形態隨脆性的不同而變化,導致高強度顆粒出現脆性損傷,低強度顆粒出現延性損傷.對于高抗壓強度材料,由于顆粒脆性,損傷后無法承受載荷.對于低抗壓強度材料,由于顆粒的延展性,顆粒破碎不會立即完成,這些顆粒在損傷后仍能承受載荷.顆粒在剪應力作用下膨脹,而孔隙率同時增加.這種剪應力下的膨脹本質是一種不穩定的高勢能態.顆粒的剪脹變形增大導致其結構不穩定,從而可能引起局部骨架結構的坍塌.剪脹變形的積累是造成水泥橢球顆粒局部骨架結構坍塌的原因之一.因此,在研究顆粒的破碎機理時,可通過單個顆粒的細觀和宏觀力學特性進行研究.

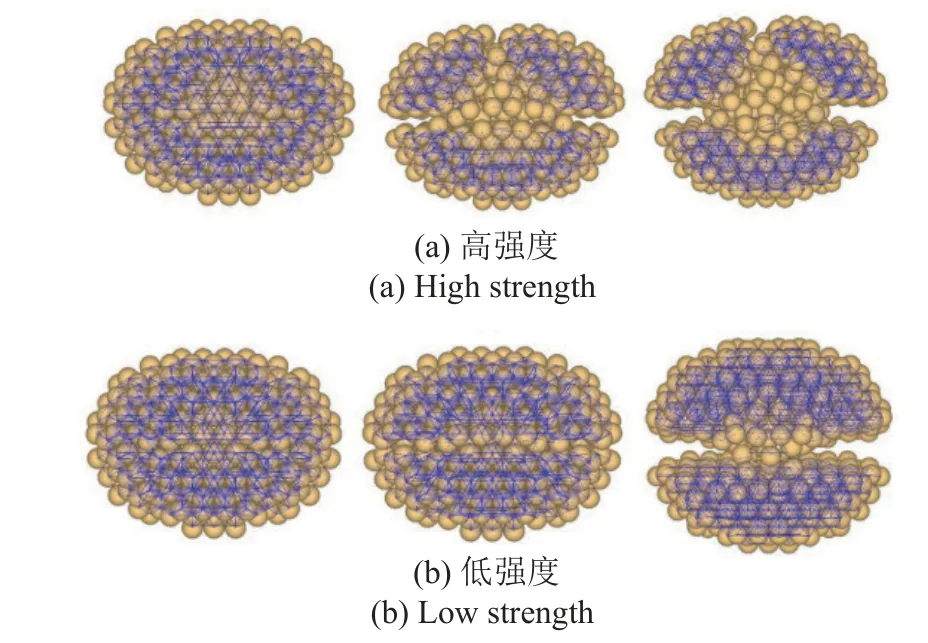
圖7 橢球體顆粒整體破碎過程演化(俯視圖,顆粒間線代表接觸黏結)[29]Fig.7 Evolution of ellipsoidal particle disintegration process as a whole(top view,interparticle lines represent contact bonding)[29]

1.1.3 黏結?破碎法在工程中的應用

由于黏結顆粒法可以構造復雜的顆粒形態,在實現顆粒破碎的模擬中可以對顆粒強度進行表征,因此,在分析此類工程問題時可以采用該方法.

鐵路道砟一般采用離散元方法建立數值模型,在列車的作用下會發生破碎.Lim 等[30]采用黏結顆粒法構造道砟的三維非規則幾何形態顆粒,并進行了單顆粒壓碎試驗和側限壓縮試驗,研究結果與物理實驗進行對比從而證明模擬結果的準確性,如圖8 所示.

圖8 加載前黏結道砟顆粒的分布情況[30]Fig.8 Distribution of bonded ballast particles before loading[30]

對海冰與海洋結構相互作用的研究,一般采用離散元方法建立海冰的數值模型,在海洋結構的作用下海冰會發生破碎,因此,海洋工程中海冰的破碎是顆粒材料破碎的重要應用領域.Lubbad 等[31]針對冰船相互作用過程,考慮了浮冰破碎后形成的小的浮冰大多會被推到一邊、旋轉或淹沒的復雜情況,建立了一個實時模擬船冰相互作用過程的數值模型,并將新的解析閉合解用于表示破冰過程.利用PhysX 求解計算域內所有浮冰6 自由度剛體運動方程.圖9 為錐體結構的破冰過程.其中浮冰采用多面體黏結單元模擬,破碎后的黏結單元不發生二次破碎,但也不會被刪除,將參與到離散元計算中并對結構產生作用.針對海洋工程結構物與海冰作用下產生的海冰破碎過程,季順迎團隊發展了球體[32]和多面體[33]離散元方法,建立了海冰的黏結破碎模型,并將其應用于海洋工程的破冰過程中,如圖10所示.

圖9 錐體結構的破冰過程[31]Fig.9 Ice breakage process of cone structure[31]

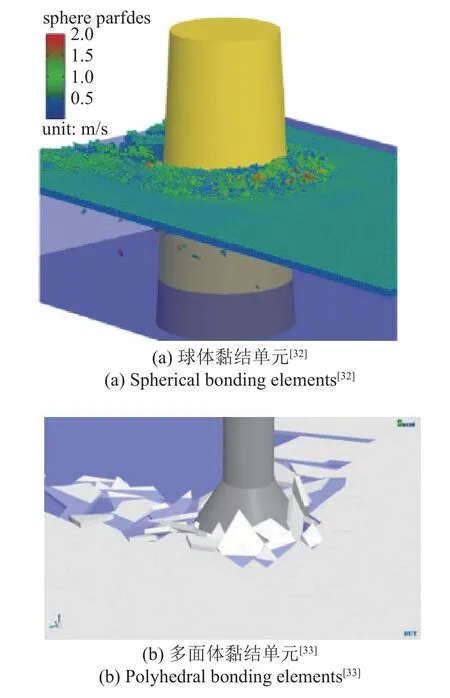
圖10 平整冰與海洋工程結構物互相作用并發生破碎Fig.10 Interaction and fragmentation between flat ice and marine engineering structures

此外,徐永福[34]采用離散元軟件PFC-2D 通過黏結單元法構造了粗粒土模型,并討論了直剪試驗中基礎顆粒間的黏結力、黏結顆粒的孔隙率和粗粒土試樣的孔隙率等因素對顆粒材料體應變和剪切強度的影響.

1.1.4 黏結?破碎法的優勢及存在的問題

黏結顆粒法能夠構造復雜的顆粒形狀[15],并實現對顆粒破碎行為的力學模擬,再現了可破碎顆粒復雜的力學響應[16],可以對顆粒強度的尺寸效應和Weibull 分布特性進行一定程度的分析[35].然而,由于每個顆粒簇是由多個基礎顆粒黏結而成,模擬顆粒破碎過程將涉及大量的基礎顆粒從而影響計算效率.因此,基于黏結?破碎法的顆粒破碎分析方法在單顆粒或小規模顆粒集合體的破碎研究中具有一定的優勢.黏結?破碎法中破碎后的顆粒無法發生二次破碎,這與真實的破碎過程不符.此外,在離散元模擬中,黏結顆粒的物理參數需要通過大量的試驗進行校正[14],在模擬顆粒破碎時需要預先設定破碎路徑,為了與真實破碎現象接近,需要大量的基礎顆粒數[36].因此,黏結?破碎法面臨的主要問題是計算效率問題,且該問題是無法通過方法優化解決的,目前主要解決辦法是發展GPU 并行算法,通過提高計算機硬件來提高計算效率.

1.2 碎片替代法

1.2.1 碎片替代法的提出與發展

碎片替代法(fragment replacement method,FRM)是strm 等[37]在1998 年提出的.該方法主要實現過程如下: 當顆粒的受力情況滿足預設的破碎準則時,開始碎片替換,在將要發生破碎的顆粒所占空間中生成碎片并刪除原顆粒從而完成替換,如圖11 所示.替換后的子顆粒在非常短的時間步內以較低的速度膨脹,這可能導致局部應力增大.因此,需要控制子顆粒的膨脹量,這主要通過局部顆粒重疊量和顆粒速度來判定[38-39].

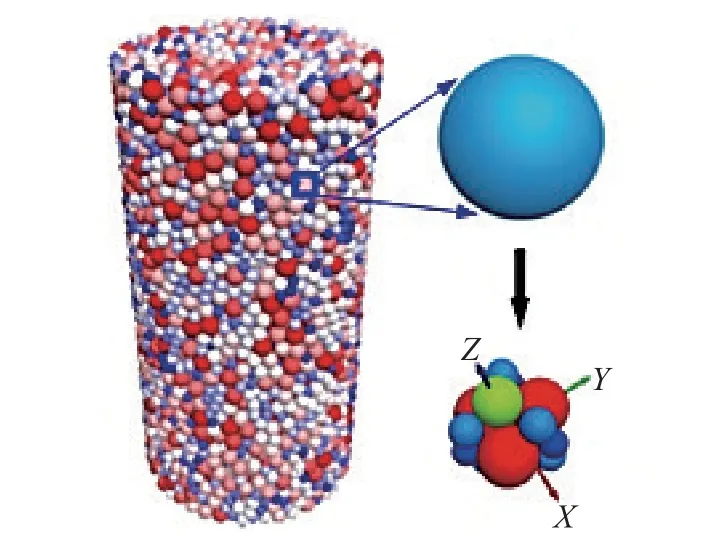
圖11 破碎替代法的破碎模式[39]Fig.11 Breakage mode of breakage substitution method[39]

碎片替代法研究顆粒破碎時,常用的破壞準則是八面體剪應力破壞準則.該準則用八面體剪應力來表示

式中,σ1,σ2,σ3分別為第1、第2、和第3 主應力.離散元方法中一個顆粒的應力張量 σij可定義為

式中,V為顆粒的體積,nc為該顆粒接觸的總數,為接觸力,為接觸中心的支向量,σ1,σ2和 σ3則分別對應于 σ11,σ22,σ33.在模擬過程中,當離散元計算得到的八面體剪應力超過設定的容許八面體剪應力q時,則認為顆粒破碎.De Bono 等[25]指出q=0.9σf=0.9Ff/d2,其中,σf為 顆粒的破碎強度,Ff為單顆粒徑向壓縮試驗中顆粒的峰值破碎力,d為顆粒的粒徑.根據Weibull 分布理論,每個顆粒的破碎強度 σf可表示為

式中,Ps(d),m,σ0,d0分別為顆粒存活概率、顆粒破碎強度的Weibull 模量、顆粒特征破碎強度和顆粒特征破碎強度對應的顆粒粒徑.其中顆粒破碎強度的尺寸效應通過 (d/d0)?3/m體現.

?str?m 等[37]提出了3 個構建碎片替代模式的標準: 盡量減少碎片數量,這是為了避免多個破碎發生后,碎片數目的迅速增加導致計算成本增大;合理布置碎片顆粒,以達到破碎時局部應力突減的效果;替代破碎顆粒的碎片的粒徑分布應盡可能與實際情況相符.?str?m 指出這3 個準則很難同時滿足.

Tsoungui 等[40]建立的碎片替換模式包含4 種尺寸12 個子顆粒,并采用二維離散元數值方法對側限壓縮試驗進行了模擬,結果顯示,該碎片替代模式能夠很好地模擬顆粒破碎的過程.Lobo-Guerrero等[41]采用碎片替代法,通過用許多不同大小顆粒的組合替換一個在拉力中失效的顆粒,模擬顆粒材料在不同雙軸應力組合作用下的破碎演化,并將顆粒材料在這些條件下的破碎過程可視化.

此外,Ben-Nun 等[42]采用兩種新的替代模式對顆粒集合體在側限壓碎時的拓撲結構對自組織特性的影響進行了分析.楊貴等[43]基于Ben-Nun 提出的替代模式發展了兩種新的碎片替代模式用于粗粒料破碎行為的研究.以上研究證明基于碎片替代法的顆粒破碎模擬可有效分析可破碎顆粒的力學響應.然而,以上均為二維替代模式,真實顆粒均處于三維環境中,且三維情況下顆粒材料的力學行為更加復雜,開展三維顆粒破碎研究具有更加重要意義.

近些年,三維情況下基于碎片替代法的顆粒破碎分析方法也得到了發展.例如,McDowell 等[44]通過在初始顆粒邊界內放入有一定重疊量的軸對稱的等粒徑小顆粒的方式,構建3 種碎片替代模式,用于側限壓縮試驗中顆粒細觀力學特性分析,如圖12 所示.Marketos 等[45]采用構建的替代模式研究了砂巖顆粒的開裂過程,重點關注了壓縮帶的萌生和擴展過程.Tavares 等[46-47]根據應力的施加位置人為設置母顆粒內部的顆粒碎片,其中較大的碎片在垂直于引起破碎的應力方向上,并且碎片顆粒在該方向上具有重疊量,較小的碎片排列在剩余的空間,通常較小的碎片與較大的碎片之間也有重疊量,如圖13 所示.初始狀態的重疊量是為了保證體積守恒,但這會引起母顆粒產生爆炸力,為了消除這個爆炸力,其中一個方法是使用松弛因子來限制由粒子重疊量計算得來的法向力.另一種簡單的方法是人為消除碎片生成時產生的重疊量,只允許母顆粒之間真正重疊量的存在.

圖12 碎片替代法研究壓縮作用下顆粒破碎的演化過程[44]Fig.12 Fragment substitution method for studying the evolution process of particle fragmentation under compression[44]

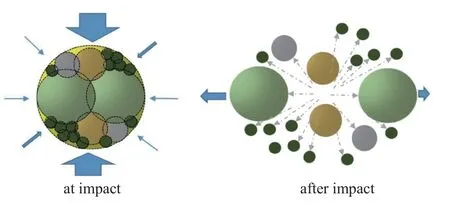
圖13 碎片的替代方案[47]Fig.13 Alternative scheme for fragments[47]

由于碎片替代法中替代顆粒的尺寸直接影響模擬效果,因此,眾多的專家學者對顆粒破碎過程的尺寸效應進行了研究.Ciantia 等[48]采用碎片替代法進行了側限壓縮數值試驗,研究了顆粒破碎的尺寸效應.Zhou 等[49]借鑒等粒徑三碎片替代方法研究了主應力對可破碎顆粒材料宏細觀力學響應的影響.為了使碎片粒徑分布盡可能地符合實際情況,Zhou 等[50]又構建了新的三維碎片替代模式,對可破碎顆粒破碎過程的尺寸效應進行了研究.Cil 等[51]采用所提出的替代模式,進一步研究了顆粒破碎能量的尺寸效應.通過以上研究,對顆粒破碎過程中的尺寸效應有了更深入的理解和探索.Tavares 等[46]認為顆粒的破碎程度可以通過一個參數t10來表征,t10表示小于母顆粒尺寸 1/10 的碎片的比例,并通過以下表達式來計算顆粒的破碎程度,其中,A和b′為由實驗數據擬合的模型參數,E50b為發生破碎的顆粒的斷裂能的中位數,為破碎過程中顆粒可用的能量.t10值越高,子代顆粒尺寸分布越細.

EDEM 在考慮單顆粒破碎時是基于碎片替代法實現的.EDEM 在研究單顆粒破碎過程時可直接獲取粒徑分布、破碎率等數據,直觀展示破碎效果,模擬速度非常快,但模擬結果目前無法體現破碎后的物料料型.

1.2.2 碎片替代法的破碎準則研究

目前,采用碎片替代法研究顆粒破碎過程時,破碎準則并沒有統一的標準.現存在的破碎準則均基于一定的假設并做了相應的簡化.?str?m 等[37]認為基于碎片替代法的破碎準則主要可以歸結為兩類:一是基于應力的判定準則,即通過對顆粒的應力設定閾值,當應力大于所設定的閾值時顆粒發生破碎;二是基于力的判定準則,即通過對顆粒的接觸力設定閾值,當最大接觸力大于所設定的閾值時顆粒發生破碎.其他的破碎準則均是在這兩種準則的框架下發展起來的.

假設最大接觸力引起顆粒局部應力集中從而導致顆粒破碎[52-53],那么最大接觸力可以作為破碎準則.Lobo-Guerrero 等[41,54-55]在二維模擬中對顆粒受力情況進行了簡化,認為當接觸數目不大于3 時,顆粒的受力情況可以類比于巴西圓盤試驗.基于以上假定,采用顆粒的特征拉應力 σt=2P1/(πLD) 作為顆粒破碎的判定條件,即 σt＞σtmax,也 即P1＞σtmaxπLD/2,其中P1為作用力,L為單位長度,D為盤直徑.

由于配位數對顆粒破碎有一定的影響[40,56],在力判定準則中引入配位數的影響,以上假定不再適用,即配位數大于3 時顆粒仍可能發生破碎[57].根據物理試驗結果建立球形顆粒在徑向加載時的最大流動剪切強度公式[58],當配位數在6～12 時該公式同樣適用[59].通過以上公式Ciantia 等[48]求得顆粒最大接觸力閾值,進而建立三維模擬中顆粒破碎的判定準則,即kmob≤k,其中kmob和k分別為顆粒的流動強度和固有強度,當流動強度大于固有強度時顆粒發生破碎.選取3 種不同破碎難易程度的材料,張科芬等[60]對其進行破碎模擬,證明以上破碎準則適用于離散元中球形顆粒的破碎模擬,并且能夠反映顆粒的真實破碎過程.Cil 等[51]基于顆粒材料特征強度的3 種尺寸效應公式發展了3 種不同的力判定標準,并通過側限固結試驗研究了采用上述3 種力判定準則時顆粒宏細觀力學行為的不同.

根據均勻化思想發展了應力判定準則假設外載荷作用下顆粒內部的應力均勻分布,是顆粒受力狀態的整體考量.半徑為R的顆粒受到任意力作用時,其平均應力張量為是顆粒的接觸數目,分別為接觸點(c)處的單位法向量沿i方向的分量和沿j方向的接觸力,Vp為顆粒的體積.其中,以等效力張量為破碎準則的本質是通過顆粒的特征強度判定顆粒是否發生破碎[57].顆粒的受力情況可以簡化為靜水壓力和偏應力,采用等效二維Drucker-Prager 準則判定顆粒的破碎情況[40].然而,由于顆粒間的接觸十分復雜,當存在多個接觸力時顆粒可能處于高靜水壓力、低偏應力的狀態,在這種情況下顆粒的破碎現象不容易發生,此時平均應力判定準則不在適用.針對以上情況,八面體剪應力破碎準則被提出并通過單顆粒壓碎試驗獲得該準則中特征拉應力的閾值[44,61];帶截斷的Mohr-Coulomb 準則也可有效解決平均應力判定準則不適用的情況[49-50,62];楊貴等[43]通過對顆粒的拉裂破壞和剪切破壞情況提出了不同的破碎準則.

以上兩種判定準則在一定程度上可以反映顆粒的破碎機制,然而,由于其均在一定假設的前提下提出的,且進行了一定的簡化,所以無法完全描述顆粒復雜的破碎行為.此外,對破碎準則的選取并沒有特定的標準,選取不同的破碎準則獲得的顆粒系統孔隙率和級配的演化過程的正確性也并未得到驗證.此外,二維和三維問題存在較大差異.因此.針對三維問題提出一套全面的、準確的選取破碎準則的方法是十分必要的.

1.2.3 碎片替代法在工程中的應用

由于碎片替代法可以實現二次破碎,且對于不考慮體積守恒和對破碎顆粒形態要求不嚴格的工程問題,可以采用該方法實現顆粒的破碎研究,同時,碎片替代法在大規模的破碎過程問題研究中也有較大的優勢,因此在以下工程問題中得到廣泛應用.

碎片替代法在巖土工程中具有廣泛的應用,如通過模擬巖體破碎的過程來預測巖體的破碎區域、巖塊大小分布、巖體的穩定性等[63];通過模擬地下開挖過程中巖土體的破碎行為,預測巖土體的破碎區域、位移和變形情況,這對于開挖工程的設計和施工具有重要意義[64];該方法還應用于模擬巖土體在振動載荷下的破碎行為,如在振動臺試驗中模擬土體的破碎過程,研究振動對土體強度和穩定性的影響;在模擬地下爆破引起的巖土體破碎過程中可獲得爆破對周圍巖土體的影響,如爆破震動對周圍地基的影響、爆破引起的巖層破碎區域等;此外,碎片替代法可以用于預測巖土材料的力學性質,如彈性模量、斷裂強度等,這對于巖土工程設計和材料選取具有重要意義[65].

Lobo-Guerrero 等[55]發展的碎片替代模式包含3 種不同大小共8 個子顆粒,并通過二維離散元數值方法研究了由于顆粒材料破碎引起的鐵路道砟級配的變化對鐵沉降變形的影響,如圖14 所示.

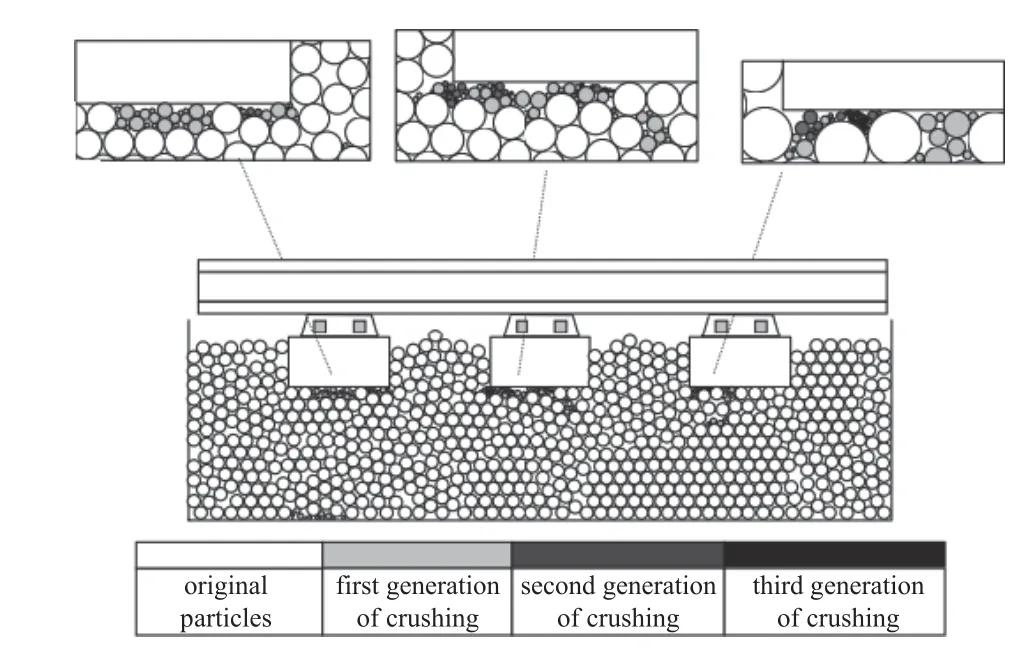
圖14 碎片替代法在鐵路道砟顆粒材料破碎中的應用[55]Fig.14 Application of fragment substitution method in railway ballast particle breakage[55]

張科芬等[60]基于局部應力集中的點載荷破碎準則,采用碎片替代法開展了3 種不同破碎難易程度材料的數值模擬.其中,為了保證破碎前、后顆粒之間的平衡,利用阿波羅填充和膨脹法,并引入尺寸因子來表征不同粒徑的顆粒強度.

1.2.4 碎片替代法的優勢及存在的主要問題

基于碎片替代法的顆粒破碎數值方法在一定程度上再現了顆粒的破碎過程,且該方法能夠實現顆粒的二次破碎.碎片替代法為較大規模顆粒破碎過程分析和細觀尺度的機理研究提供了一定的思路.然而,由于碎片替代模式的主觀性導致模擬結果與真實的顆粒形態及破碎過程存在較大的差異;三維模擬中顆粒破碎的判定準則并不完善.對以上問題的有效解決將促進碎片替代法的發展和應用.

2 基于離散元?有限元耦合方法的顆粒破碎數值算法

當參考連續介質力學對材料破碎的研究方法并結合顆粒材料的離散特性,可采用離散元?有限元耦合的方法對顆粒破碎進行數值研究.以下將介紹比例邊界有限元方法、組合有限元?離散元方法以及典型的內聚力模型.

2.1 比例邊界有限元法

2.1.1 比例邊界有限元法的提出與發展

比例邊界有限元法是由Song 等[66]提出的一種新的半解析方法,該方法是基于有限單元和邊界元方法提出的,同時擁有有限元法和邊界元法的優點,已經在一些工程領域中的動力學和靜力學問題研究中得到了應用.比例邊界有限元法相對于有限元法和邊界元法計算過程更簡單有效,并可得到工程滿意的結果.Ooi 等[67]發展了適用于任意邊數的凸多邊形比例邊界有限元法.凸多邊形比例邊界有限元僅用一個多邊形單元就可以模擬具有任意邊數的凸多邊形顆粒,并得到其變形和應力狀態.

比例邊界有限元法實現顆粒的破碎過程時需要對每個顆粒的應力?應變進行完整分析,然后根絕準則來判定顆粒內部的破壞點,當破壞點的數量達到一定比例后,認為該顆粒發生破碎.比例邊界有限元法認為顆粒破碎的路徑是直線,所以采用加權最小二乘法對破壞點進行擬合,將破碎點連接起來獲得破碎路徑,從而使顆粒破碎為兩部分.該方法不需要對破壞路徑的位置和方向進行預定義.破碎后產生的顆粒在下一時間步中參與計算.羅滔等[36]采用比例邊界有限元方法與離散元方法結合,對堆石料的雙軸壓縮實驗進行了模擬,結果如圖15 所示.

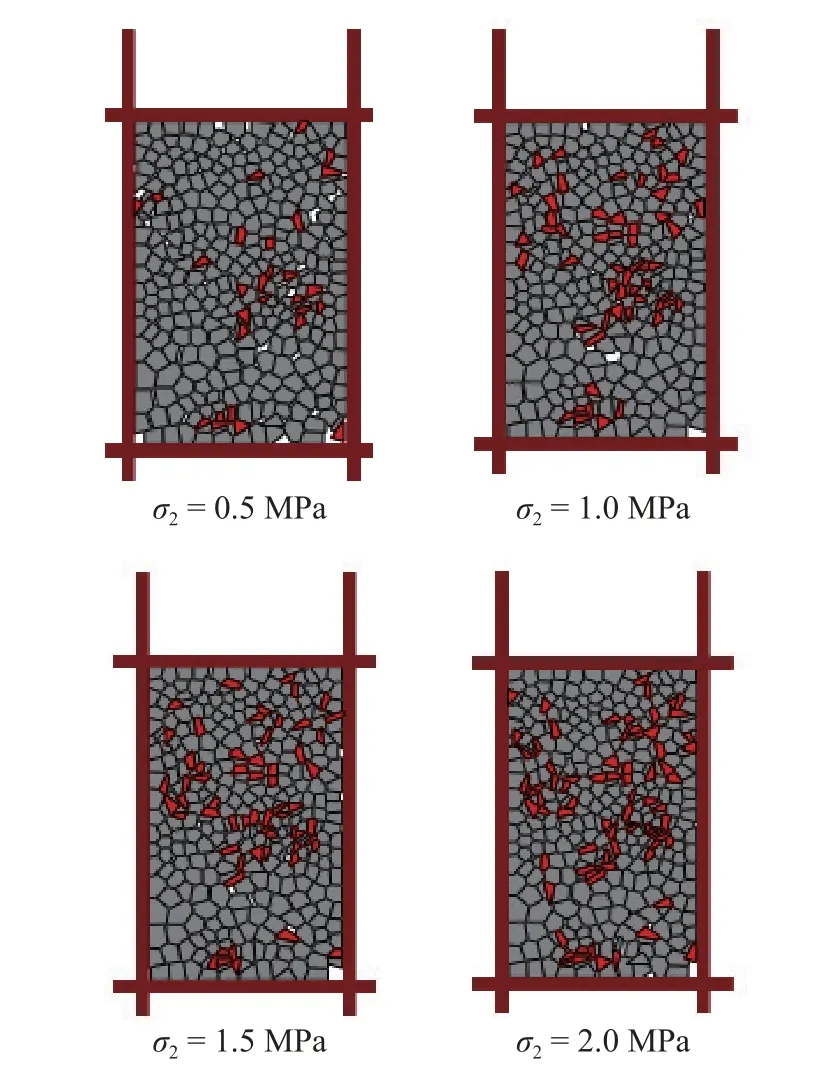
圖15 加載結束后不同圍壓下的顆粒破碎分布[36]Fig.15 Particle fragmentation distribution under different confining pressures after loading[36]

2.1.2 比例邊界有限元法的破碎準則

為了研究顆粒的破碎行為,需要建立相應的破碎準則,由于比例邊界有限元方法已經計算獲得了每個顆粒內部的應力場,因此,采用基于應力的破壞準則判斷顆粒是否破壞.判斷破壞的流程為: 首先在顆粒內部選取具有代表性的樣本點,如圖16 所示,基于Hoek-Brown 破碎準則判斷樣本點是否破壞;當破壞樣本點的數量達到一定比例時顆粒破壞;比例邊界有限元方法假設顆粒的破壞路徑為直線,并通過加權最小二乘法對破壞點進行擬合得到破壞路徑;沿著破壞路徑將顆粒分為兩個顆粒[68].

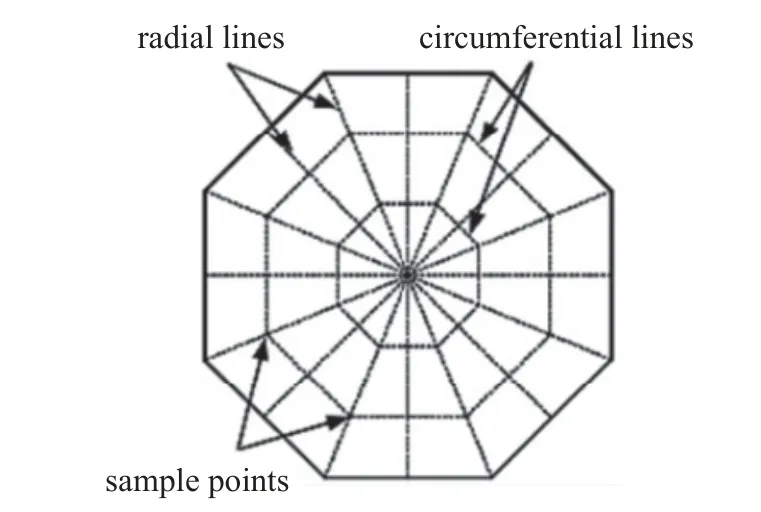
圖16 樣本點的分布Fig.16 Distribution of sample points

為了判斷樣本點是否破壞,應用Hoek-Brown 破壞準則[68]

式中,σt為抗拉強度;σ1f是由式(4)得出的第1 主應力,如果安全系數Fs＜1 則表示此點破壞,由Hoek-Brown 準則得到的破壞點如圖17 所示.

圖17 由Hock-Brown 準則得到的破壞點Fig.17 Failure points obtained from the Hock-Brown criterion

2.1.3 比例邊界有限元法的優勢及存在的主要問題

在一定程度上,比例邊界有限元方法從細觀尺度揭示了顆粒破碎機制.比例邊界有限元方法計算顆粒內部的應力分布,從而實現顆粒的破碎過程,顆粒破碎產生的新的顆粒將直接參與到離散元和比例邊界有限元的計算中,比例邊界有限元方法對顆粒破碎的研究無需預定義任何子顆粒或者網格重劃分[36].然而,該方法需要人為設計樣本點的分布,且其破碎路徑均為直線,因此,比例邊界有限元法的主觀性很強,很難客觀反映顆粒破碎真實過程,發展從細觀尺度反映顆粒破碎真實過程的數值方法迫在眉睫.

2.2 組合有限元?離散元方法

2.2.1 組合有限元?離散元方法的提出與發展

組合有限元?離散元方法(FDEM)是Munjiza等[69]在 20 世紀90 年代為解決混凝土加載中裂紋的萌生和擴展問題發展的數值方法.組合有限元?離散元方法首先對顆粒進行單元劃分,并通過接觸面單元對其進行連接,離散元法計算獲得顆粒之間的作用力作為每個顆粒應力計算的邊界條件,從而實現單個顆粒的應力?應變分析,獲得顆粒的應力狀態和變形情況.組合有限元?離散元法中顆粒沿有限單元的邊界破壞.

FDEM 采用FEM 理論作為顆粒的變形、壓裂破壞標準,通過DEM 概念來檢測新的接觸點,解決離散單元的平移、旋轉和相互作用問題[70].FDEM利用分布接觸力方法和罰函數方法解決接觸力問題,有效地處理了復雜形狀的變形問題[71].FDEM 在非線性彈性斷裂力學(NLEFM)框架下模擬裂縫的起裂和擴展過程,此外,在FDEM 中可以實現重網格技術,但在建模可破碎顆粒材料時,計算成本非常高.由于在模擬過程中沒有執行重網格,網格拓撲也沒有更新,因此在加載過程中粒子不能繼續變小.

基于FDEM 發展的顆粒破碎仿真軟件主要有中科院力學所李世海團隊的GDEM,該軟件采用有限元和塊體離散元耦合的方法對巖土工程中的顆粒材料破碎問題實現了數值分析.基于多物理場斷裂分析軟件MultiFracS 的基本理論也是有限元?離散元耦合算法,該軟件在巖土材料斷裂及破碎數值建模方面有獨特優勢,在隧道、邊坡、采礦、水利水電、爆破、非常規油氣及地熱開采等領域有重要應用價值.

2.2.2 組合有限元?離散元方法在工程中的應用

由于FDEM 方法在模擬顆粒破碎的過程時,對每個顆粒進行應力分析,因此破碎過程與實際更加相符.在對單個顆粒的破碎分析中可有效揭示顆粒的破碎機理.因此針對考慮破碎機理的工程問題,以及需要模擬的破碎過程更加接近真實情況時,可采用該方法實現.

組合有限元?離散元方法在巖土工程中得到廣泛的應用,如嚴成增等[72]將其與數值圖像技術結合,系統分析了巖體的破裂機制;Ma 等[73]采用組合有限元?離散元方法建立了巖石顆粒的數值模型,如圖18 所示,并對巖石顆粒在軸壓作用下的斷裂過程進行了模擬,系統研究了破碎前顆粒的形貌對破碎后碎片的形態和尺寸分布的影響,如圖19 所示.此外,在組合有限元?離散元方法中引入基于應力的破壞準則,并對堆石料的破碎過程進行模擬,模擬過程中無需預先定義或者假設顆粒的破壞路徑[74-75].Mahabadi等[76]使用三維FDEM 方法研究Opalinus clay 黏土頁巖地層中隧道周圍的開挖損傷區的發展.通過巴西圓盤試驗和單軸壓縮試驗,對三維FDEM 模型進行校準,結果如圖20 所示.

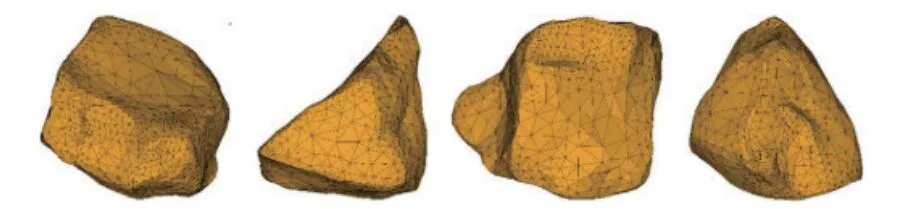
圖18 巖石顆粒的FDEM 數值模型[73]Fig.18 Numerical model of rock particles[73]

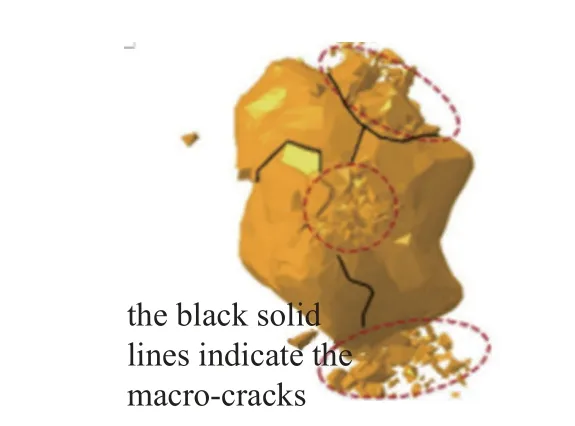
圖19 FDEM 方法研究巖石顆粒在軸壓作用下的斷裂結果[73]Fig.19 FDEM method for studying the fracture process of rock particles under axial compression[73]

圖20 采用FDEM 方法進行巴西圓盤和單軸壓縮試驗[76]Fig.20 Brazilian disc and uniaxial compression tests using FDEM method[76]

Rougier 等[77]將離散裂紋與塑性變形相結合,并采用FDEM 方法模擬二維泰勒桿的斷裂過程,如圖21 所示.其中變形采用FDEM 方法描述,塑性變形在材料嵌入坐標系中表述,乘法分解和塑性流動在拉伸空間中求解.該工作將FDEM 中的裂紋和破碎標準有效結合.

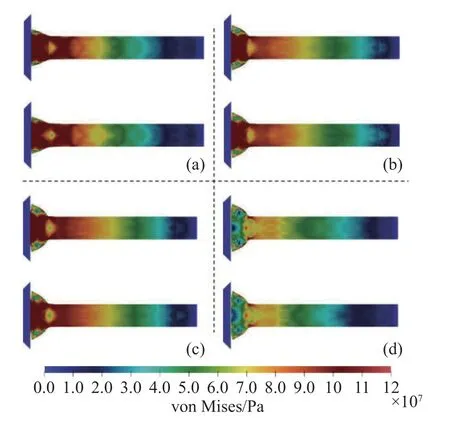
圖21 FDEM 方法模擬二維泰勒桿的斷裂過程[77]Fig.21 FDEM method simulation of the fracture process of twodimensional Taylor bars[77]

針對脆性材料的斷裂和破碎響應,Chen 等[78]采用FDEM 方法對夾膠玻璃在硬體沖擊下的斷裂和破碎過程進行了模擬,如圖22 所示,并討論了玻璃、層間和層間界面的破壞模型,證明了該模型在模擬夾層玻璃破裂時是可靠的.Lilja 等[79]采用FDEM 方法建立海冰的三維數值模型,如圖23 所示,該模型由同轉動、黏性阻尼Timoshenko 梁有限元組成的平面梁晶格與形成實際海冰的剛性離散單元的質量質心相連接.通過質心Voronoi 鑲嵌程序生成網格,由于內部存在阻尼,基于晶格的結構的機械響應依賴于應變速率和尺寸.

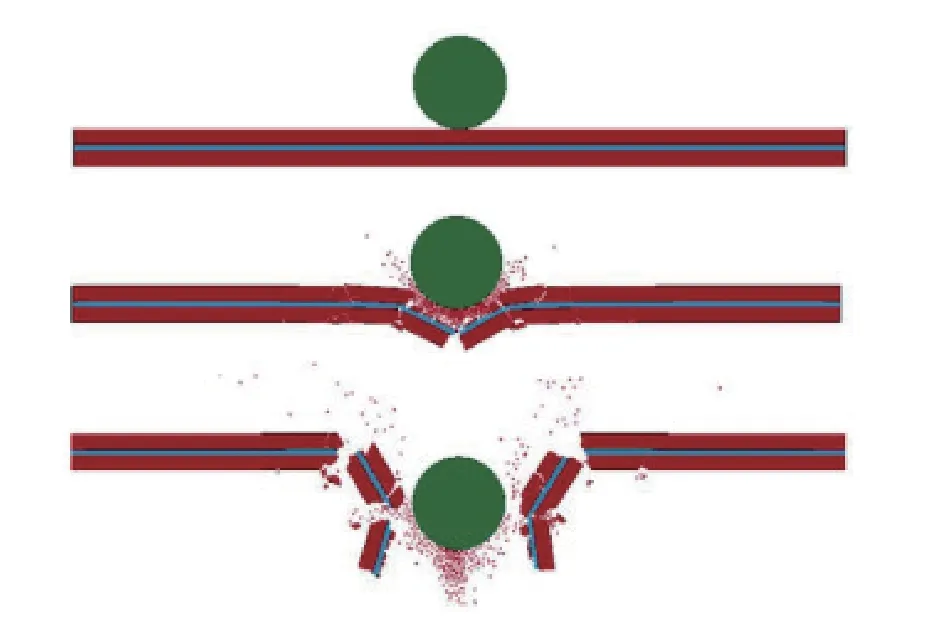
圖22 夾膠玻璃在硬體沖擊下的斷裂和破碎響應[78]Fig.22 Fracture and fragmentation response of laminated glass under hard impact[78]

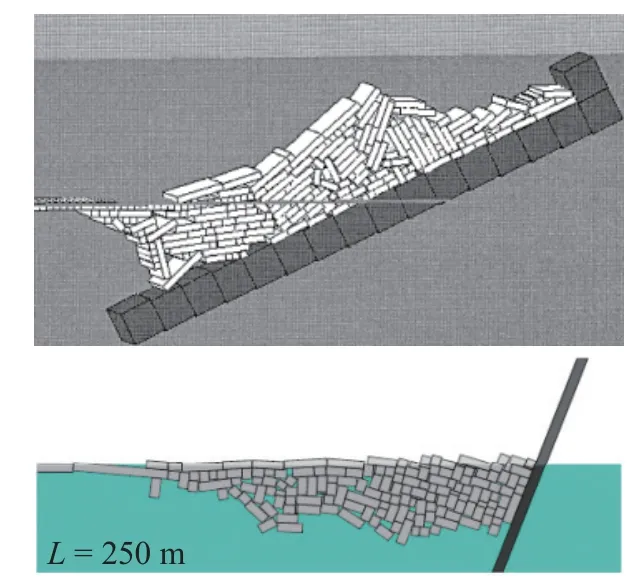
圖23 采用FDEM 方法建立海冰的三維數值模型[79]Fig.23 Establishing a three-dimensional numerical model of sea ice using FDEM method[79]

2.2.3 組合有限元?離散元方法的優勢及存在的主要問題

FDEM 方法可有效模擬顆粒的破碎過程,由于該方法對每個顆粒進行應力分析,因此破碎過程與實際更加相符.在對單個顆粒的破碎分析中可有效揭示顆粒的破碎機理.然而,由于模擬過程中需要對每個顆粒進行有限單元劃分,且顆粒的破碎只能沿著網格進行,為了獲得更為真實的破碎過程,需要網格精細化,這均導致計算成本非常大[36].這將限制了其在工程中的應用,對實際工程問題的模擬無法起到推動作用.

2.3 內聚力模型

2.3.1 內聚力模型的提出與發展

FDEM 方法中,有限元離散化以后,將黏性界面單元插入到與每個粒子相關的有離散單元中,以考慮粒子的破碎過程.本節將重點介紹黏性界面的內聚力模型(cohesive zone model,CZM)[9,80-82].內聚力模型是1960 年Dugdale 等提出的[83-84],假設裂紋的尖端是由兩個裂紋界面組成的很小的內聚區,該內聚區的本構關系就是界面上作用牽引力T與兩裂紋面間相對位移U之間的關系.內聚力模型和裂紋尖端內聚區的分布[85]如圖24 所示.

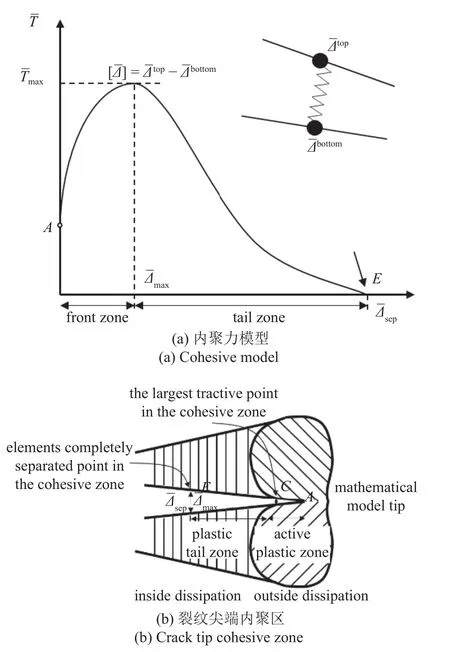
圖24 內聚力模型和裂紋尖端內聚區[85]Fig.24 Cohesion model and crack tip cohesive zone[85]

內聚力模型從未完全承載的點A開始,T隨著U的增加而增加,隨之達到應力最大值Tmax的點C,此時材料的應力承載達到最大值,材料在該點處開始出現初始損傷.隨著界面位移的繼續增大,應力開始下降,該階段為材料的損傷擴展階段,點E為材料裂紋界面完全分離點,此時材料的承載力降為0[85].內聚區應力的變化受內聚力模型和裂紋界面位移的影響,因此,針對不同的材料,應該選擇不同的內聚力模型,同時通過選取適當的參數,從而反映界面的強度、韌度等力學性能.

內聚力模型可分為基于位移的內聚力模型和基于勢能的內聚力模型.在基于位移的內聚力模型中,裂紋上下表面之間的有效牽引力可由有效分離位移的函數表示,通常稱之為牽引力分離法則.常用到的牽引力分離法則包括線性軟化、雙線性軟化、指數和梯形法則等.不同法則的區別在于與之間函數關系的不同.將有效牽引力與內聚強度σmax歸一化處理的結果如圖24(b)所示.基于位移的內聚力模型出現的裂紋擴展問題,可以在基于勢能的通用內聚力模型中得到解決.基于勢能的內聚力模型采用三次多項式表示法向牽引力,采用線性關系式表示切向牽引力[85].

早期非線性斷裂研究一般認為,當內聚區尺寸小于裂紋和試樣尺寸時,內聚力模型理論與Griffith的能量平衡理論等效.Dugdale[83]認為內聚應力的分布在數值上與材料的屈服強度相等,但這有悖于實際物理事實,Barenblatt[84]考慮內聚力分子尺度的特征,把內聚應力看作內聚區裂紋面各點處裂紋張開位移的函數,但具體的解析式無法準確給出,在大多數情況下內聚力仍被假設為常數.基于以上工作,Hillerborg 等[86]考慮顆粒的拉伸強度,采用有限元方法建立脆性材料的內聚力模型并對其斷裂過程進行模擬,實現了原有裂紋的增長、新裂紋的萌生和擴展研究,對斷裂細節進行了完整的描述.Needleman[87]通過高次多項式函數對延性材料的斷裂情況進行了模擬.Kolher 等[88]采用了分段函數描述內聚力模型的方法對鎳鋁合金的剪切斷裂性能進行了模擬.

為模擬脆性巖體的斷裂行為,清華大學徐文杰團隊[89]提出了一種針對多面體離散元顆粒設計的內聚斷裂模型(CFM),如圖25 所示.巖體被離散成一系列剛性多面體塊體,這些塊體沿邊界面的法向和剪切方向黏結在一起.黏性準則規定了CFM 的法向和剪切斷裂強度.通過在Blaze-DEM 框架中對多個圖形處理單元的并行處理,提高了CFM 在多面體模擬中的計算效率.

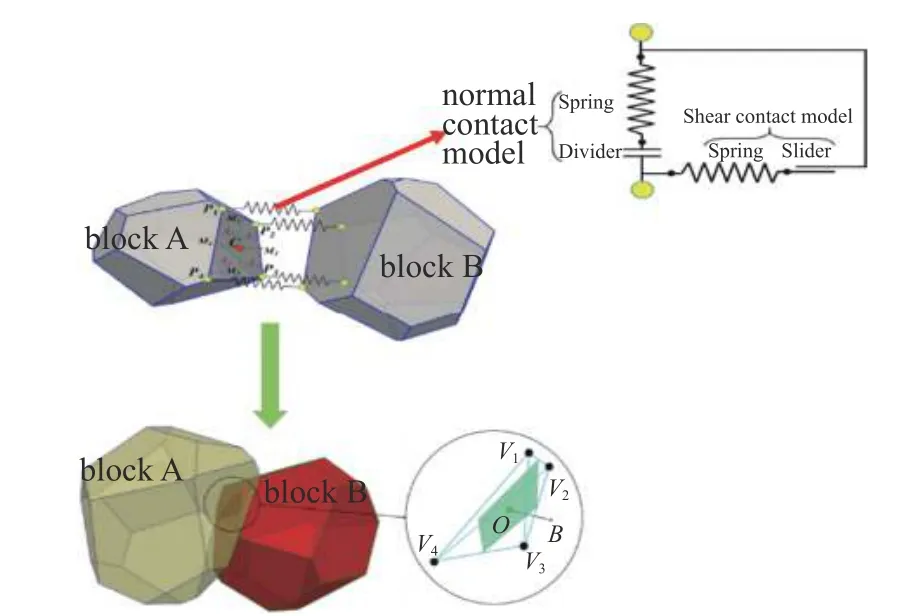
圖25 斷裂前、后的接觸模型[89]Fig.25 Model after fracture[89]

2.3.2 內聚力模型在工程中的應用

內聚力模型在處理非線性和大變形問題時具有非常強的適應性.隨著內聚力模型的改進和發展,在多種材料的斷裂問題上具有獨特的優勢,因此,在處理此類工程問題時可采用該方法.

Gui 等[90]在通用離散元編碼(UDEC)中,引入了結合拉伸、壓縮和剪切材料特性的內聚斷裂模型,用于模擬巖石動力試驗中的壓裂過程,通過缺口半圓彎曲試驗和巴西盤試驗兩個數值算例,驗證了內聚力模型對巖石動態破壞模擬的有效性.

為了模擬巖石破裂過程,廣東工業大學高偉團隊提出一種新的內聚模型本構.在該本構中,采用Mohr-Coulomb 準則作為裂紋萌生準則,建立壓縮和拉伸狀態下的牽引?分離模型,描述了巖石強壓力依賴性的力學特性.在粘結區完全破壞后,采用基于庫侖公式的摩擦模型來確定裂紋自由面之間的接觸相互作用.采用所提出的零厚度黏合單元本構,模擬了巴西盤、單軸壓縮兩個巖石破裂實例.比較仿真結果與實驗結果發現以上模型是可靠的[9],如圖26～圖27 所示.

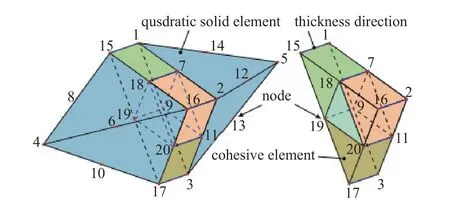
圖26 0 厚度黏合單元本構[9]Fig.26 Constitutive law of zero thickness adhesive element[9]

圖27 采用內聚力單元模擬巴西盤破裂和單軸壓縮巖石破裂實例[9]Fig.27 Simulation of brazilian plate rupture and example of rock fracture using cohesive elements[9]

2.3.3 內聚力模型的優勢及存在的主要問題

內聚力模型的理論基礎是彈塑性斷裂力學理論,該模型認為斷裂問題是非線性邊值問題,不必考慮斷裂的起裂和擴展準則,因此,適應性強,可以解決非線性和大變形問題.隨著計算機技術和有限元方法的發展,內聚力模型得到了改進和發展,已經可以解決多種材料的斷裂問題.然而,針對顆粒型材料,仍然存在計算效率的問題,因此,該方法在研究顆粒型材料的破碎問題中仍沒有得到推廣.

3 近場動力學方法及其他方法

3.1 近場動力學方法

3.1.1 近場動力學方法的提出與發展

近場動力學(peridynamics,PD)是一種新興的非局部性理論,針對模型中的非連續問題,該方法不需要任何處理,對模型中從連續到非連續的過程可以很好地處理[91-92],因此,該方法在研究離散介質的破碎問題時有一定的優勢.近場動力學方法是Silling等[93]于2004 年提出的,該方法基于長程非局部作用思想建立力學模型,通過求解空間積分型運動方程來描述物質力學行為,實現了對連續介質和非連續介質力學行為的統一描述.此外,由于損傷概念的引入,近場動力學理論對材料的損傷和裂紋的形成過程可以有效描述.因此,在處理裂紋自發萌生和擴展等非連續問題時,近場動力學理論具有一定的優勢[94].

近場動力學方法將固體材料離散為一系列具有體積和質量的物質點,每個物質點與其周圍一定區域內所有其他物質點之間存在相互作用力.如圖28所示.

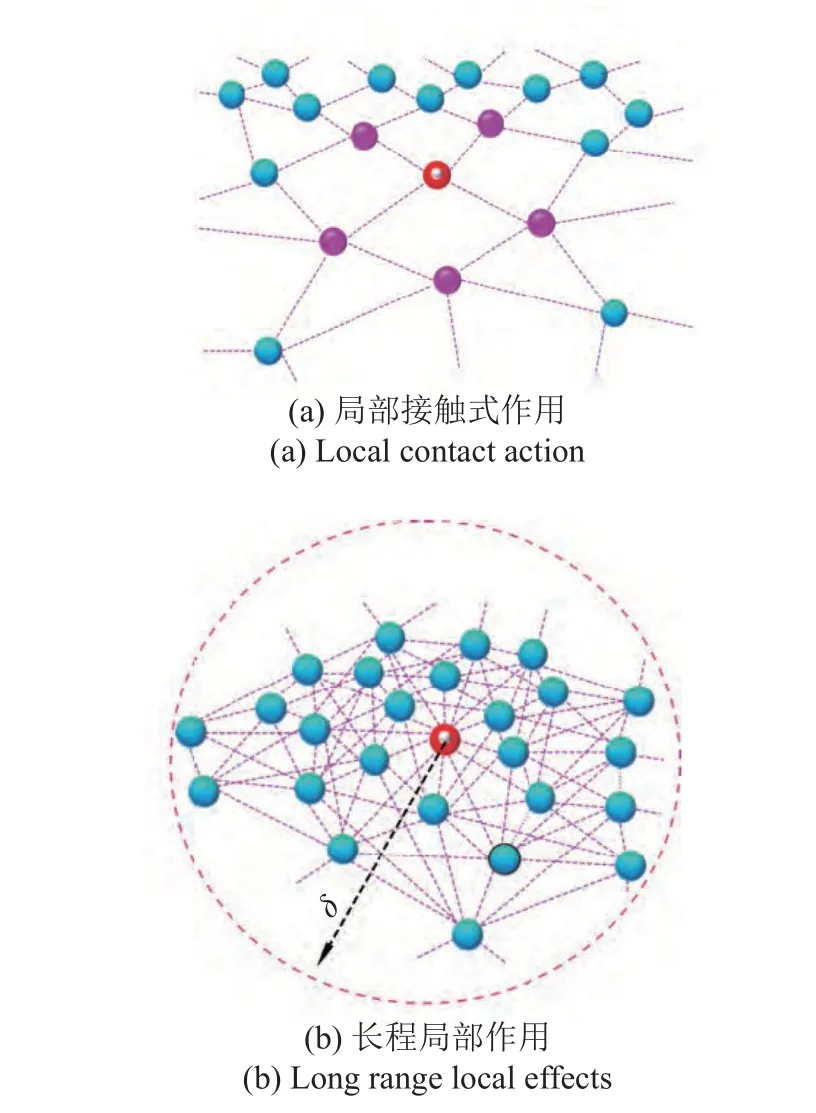
圖28 近場動力學理論的局部接觸式作用和長程非局部作用[91]Fig.28 Local contact type action and long-range non local action in peridynamics theory[91]

近場動力學理論是一種非局部連續介質力學理論,采用積分的形式表示鄰域半徑 δ 內物質點x和x′之間的相互作用力,即鍵力.物質點x的動力學方程為

近場動力學理論通常被分為鍵型(bond-based)和態型(state-based)兩種.其中鍵型近場動力學理論認為兩物質點之間的相互作用僅包含兩物質點間的鍵力.而態型近場動力學理論在分析兩物質點間的相互作用時考慮了鄰域內所有物質點對鍵力的影響.顯然,鍵型近場動力學理論是態型近場動力學理論的一種特例[91].

計算程序編寫促進了近場動力學理論的發展和應用.Silling 團隊在1998 年采用Fortran 90 語言開發了近場動力學方法的代碼EMU,并對其進行了測試,這是第一次將近場動力學理論程序化;Parks 等基于分子動力學軟件LAMMPS 開發了軟件PDLAMMPS,擴展了近場動力學理論的應用;Macek 等在經典動力學分析軟件ABAQUS 中引入近場動力學算法,促進了近場動力學理論的發展;此外,LS-DYNA 中也引入了近場動力學方法擴展程序包,并命名為DYNAPeridynamics,有效地結合了現有商業軟件和近場動力學方法在處理動力學問題的優勢;近期,桑迪亞國家實驗室基于離散單元法開發了開源軟件Peridigm,該軟件兼容了Cubit 網格生成工具和Paraview 可視化程序,將近場動力學方法平臺化,具有人機交互性好、計算穩定、后處理方便、實用性強等優點[91];趙吉東團隊[95]開發了PD-NSCD 混合法的代碼,并應用于顆粒材料連續破碎過程的研究,自主開發代碼實現近場動力學理論部分,使用開源代碼Project Chrono 進行基于NSCD 的離散建模.同時,通過MATLAB,Python,C 語言,Fortran 等語言進行近場動力學數值計算與分析也是部分學者在處理實際問題時采用的手段[96-97].

趙吉東團隊[95,98-99]開發的PD-NSCD 混合法,采用非光滑接觸動力學模擬顆粒系統的剛體運動以及顆粒間相互作用,利用近場動力學理論分析單個顆粒的破碎.基于近動力學和物理引擎提出一種新的混合計算框架來模擬機械載荷下的可破碎顆粒材料.在此框架下,利用近場動力學方法模擬單個粒子的破碎,利用基于非光滑接觸動力學方法的物理引擎模擬粒子的剛體運動和粒子間的相互作用.該混合框架可以對顆粒破碎過程進行模擬,并實現連續破碎過程中不規則顆粒形狀的表征和模擬,克服了許多現有方法面臨的缺陷和挑戰.其工作為研究顆粒破碎的復雜過程提供了一種有效的方法,為今后研究可破碎顆粒材料的微觀結構行為提供了參考.圖29 顯示了近場動力學分析初始化和構造粒子的完整過程[98],其中,圖29(a)為受接觸力作用的顆粒,圖29(b)為對離散粒子進行的近動力學分析,圖29(c)未顆粒破碎的近動力學分析結果,圖29(d)為物理引擎中的模擬粒子,圖29(e)為破碎粒子的拆分視圖.圖30～圖31 為砂石顆粒連續破碎過程的數值模擬結果[95,98].

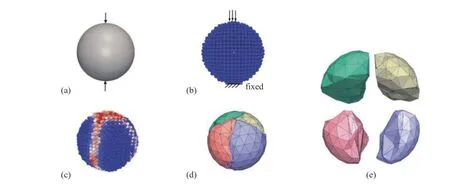
圖29 顆粒破碎建模過程示意圖[98]Fig.29 Schematic diagram of particle breakage modeling process[98]

圖30 球形顆粒模擬砂石顆粒連續破碎過程[98]Fig.30 Simulation of continuous breakage process of sand and stone particles with spherical particles[98]

圖31 多面體顆粒模擬砂石顆粒連續破碎過程[95]Fig.31 Simulation of continuous breakage process of sand and gravel particles using polyhedral particles[95]

3.1.2 近場動力學方法在工程中的應用

目前,近場動力學理論已經在多個領域得到了應用[100].如混凝土壓碎[93,101]、金屬沖擊[102]、子彈穿透[103-104]、土體[105-107]和陶瓷破碎[108]、薄膜撕裂[109]以及玻璃沖擊[110]等.目前,特別是在巖石力學研究中,近場動力學方法已經成功模擬了水壓致裂破壞過程[111],對于預制裂紋的萌生、擴展和破壞過程模擬,近場動力學方法也是有效的.通過近場動力學理論,Ha 等[112]、朱其志等[113]和王振宇等[114]研究了單條預制裂紋在單軸壓縮條件下裂紋的演化過程;Lee等[115-116]研究了含有預制裂紋巖石的翼型裂紋和次生裂紋的形成過程;Rabczuk 等[117]采用雙鄰域近場動力學模型對含多條隨機裂紋的巖石的破壞過程進行了研究.此外,Zhou 等[118-121]引入摩爾庫倫準則和極限張拉破壞準則,對預制裂紋的巴西圓盤[120-121]、三點彎曲[119,121]、單軸壓縮[119]以及雙軸張拉[118]進行了數值模擬.

Hu 等[110]采用近場動力學方法分析了玻璃板的損傷模式,其中沖擊速度從61～200 m/s 不斷增加.將實驗結果與簡化模型的近場動力學模擬結果進行了比較,如圖32 所示.實驗觀察到的主要斷裂模式是由3 種沖擊速度的每一種測試的近場動力學模型捕獲的.該方法通過進一步改進邊界條件以實現對多層體系的沖擊造成的脆性損傷更準確的模擬.近場動力學計算模型揭示了玻璃層復雜脆性損傷演化的早期階段,以及邊界條件對動態破裂過程的影響.

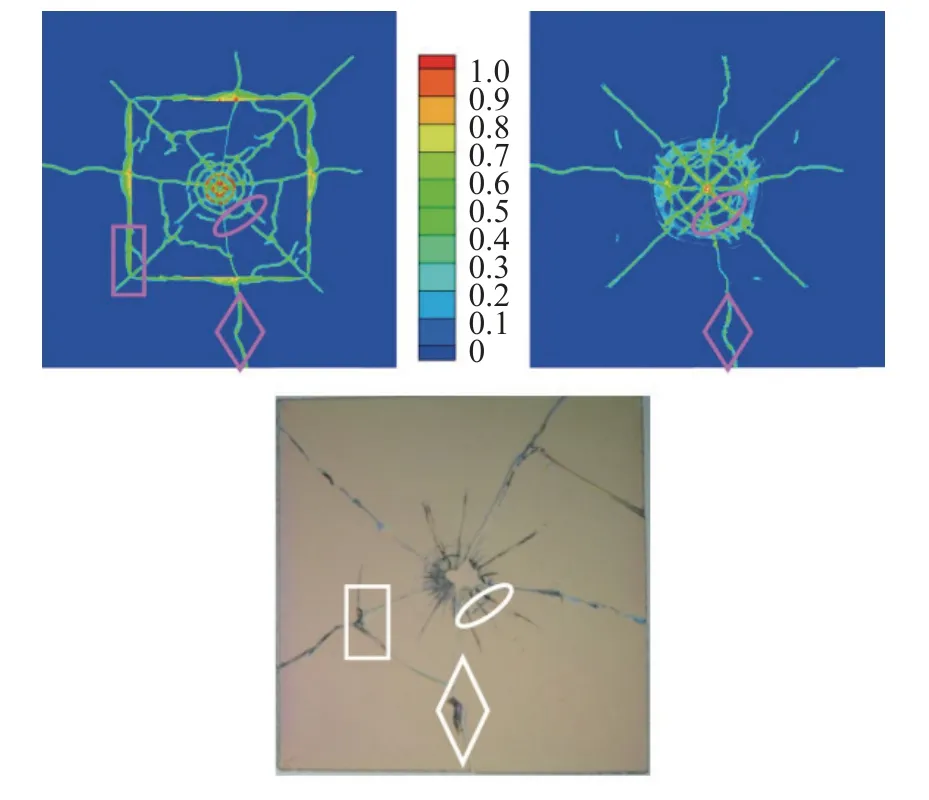
圖32 撞擊速度為61 m/s 的破碎圖,以上分別是玻璃正面、底面和實驗結果[110]Fig.32 Fragmentation diagram with an impact velocity of 61 m/s,showing the front,bottom,and experimental results of the glass[110]

Rabczuk 等[117]提出了一種用于顆粒狀和巖石狀材料斷裂的雙層近場動力學(DH-PD)方法.與離散裂紋方法相比,DH-PD 方法不需要任何裂紋表面的表示形式,也不需要任何標準來處理復雜的裂紋形態,裂紋路徑是模擬的自然結果.在該方法中作者提出了一種新的模擬壓縮裂縫接觸和約束侵徹條件的懲罰方法.該方法被應用于地質力學的一些基準問題,圖33 為采用雙層近場動力學方法研究方形板裂紋擴展的數值模擬結果.

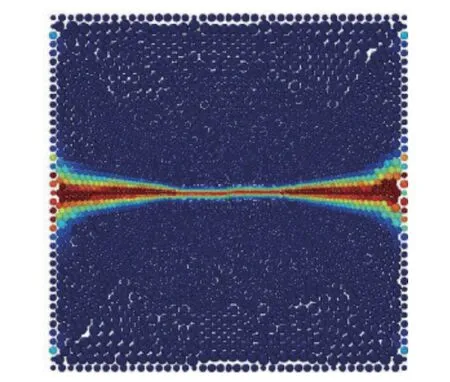
圖33 雙層近場動力學研究方形板中裂紋的擴展[111]Fig.33 Double layer Peridynamics study on crack propagation process in square plates[111]

Shen 等[101]采用近場動力學理論分析混凝土結構的損傷和漸進破壞.建立了混凝土柱單軸受壓非局部近動力模型,如圖34 所示.模擬結果表明,混凝土近動力體的裂縫是自發形成的.此外,模擬結果也展現了基于近場動力學理論建模混凝土損傷累積和漸進破壞的優勢.Shen 等的研究為分析復雜的不連續問題提供了一種新的思路.

圖34 單軸壓縮混凝土柱的近場動力學模擬[101]Fig.34 Peridynamics simulation of uniaxial compression concrete columns[101]

3.1.3 近場動力學方法的優勢及存在的主要問題

近場動力學方法克服了基于局部作用思想建模和求解空間微分方程在處理非連續問題時遇到的奇異性困難,突破了經典分子動力學方法在計算尺度上的局限,在宏觀和微觀非連續力學問題分析中具有明顯的優勢[91].僅經過十幾年的發展,近場動力學在模擬材料非連續破壞方面已展現出明顯的優越性.因此,隨著近場動力學理論與應用研究的不斷深入將促進巖石力學的進一步發展.

目前,近場動力學模型中的“邊界效應”問題是需要解決的一個重要問題[122].對近場動力學模型中自由邊界附近的物質點進行積分時,會出現鄰域不完整和受力不平衡的現象,這導致了“邊界效應”問題的產生.無外力作用下發生自由膨脹時,由于積分域不完整導致模型自由邊界附近物質點的鍵力分布不對稱,導致物質點的受到非平衡力,降低了計算精度.鍵型近場動力學模型中的微模量c被視為常數也會引起“邊界效應”問題.目前,主要采用以下辦法處理近場動力學模型中“邊界效應”問題: (1)對自由邊界附近物質點進行體積修正或虛構邊界層;(2)進行力密度修正;(3)能量密度修正[91].然而,上述方法僅僅削弱了“邊界效應”的影響,而沒有解決邊界問題的根本.

近場動力學方法的計算效率相對傳統數值計算方法較低,主要原因在于其在鄰域半徑范圍內進行積分,且求解過程以顯式計算為主.因此,計算時間步需要足夠小才能獲得穩定解,這將導致計算量增大.雖然近場動力學方法在解決非連續問題上具有優勢,但其不完善性也限制了其在大規模問題上的應用.為了提高計算效率,目前研究者們將近場動力學方法與傳統數值方法相結合.同時,隨著計算機技術的快速發展和近場動力學理論的不斷完善,計算效率問題正在逐步得到解決.

3.2 其他方法

除了以上論述的數值方法外,還有一些方法本文未詳細介紹,如Harmon 等[123]提出的水平集切割法,武漢大學王橋團隊[124-125]和周偉團隊[126]發展的相場理論方法,劉彪等[68]采用的邊界元方法,以及物質點法等.這些方法都在顆粒破碎的研究過程發揮了重要的推動作用,為今后發展更為可靠、高效的數值方法奠定了基礎.

4 總結與展望

4.1 總結

顆粒破碎是顆粒材料研究中的關鍵內容.目前,顆粒破碎的研究已經取得了一定的成果,并在工程領域得到廣泛的應用,解決了一定的實際問題.然而,現有的方法大多是從現象出發,缺乏對顆粒破碎機理的明確研究,因此,截止目前,對顆粒材料的破碎機理認識仍不清晰.此外,現有的方法一般預設了破壞路徑,這與真實的破碎過程存在一定的差異;有的方法僅可以破碎一次,破碎后的顆粒無法實現二次破碎,這與實際也是不符的;若不提前預設破壞路徑,且顆粒可以發生多次破碎,那么計算效率將會非常低.面對以上問題,亟待提出一種從機理出發不需要預設破壞路徑且可以發生多次破碎的研究顆粒破碎的高效數值方法.

4.2 展望

針對顆粒破碎的數值研究,目前仍有一些問題存在,這將是今后研究的主要內容和方向.

首先,為了探究顆粒破碎的內在機理,則需要從破碎的本質出發,考慮顆粒真實破碎的內在原因.從以上內容不難看出,目前有關顆粒破碎的機理研究內容較少,為了揭示顆粒破碎的內在機理,必須將機理研究作為首要研究內容.

其次,當從顆粒破碎的現象描述出發,則需要考慮顆粒破碎程度的度量指標問題.對顆粒的破碎程度以及破碎后顆粒進行描述,這就需要有合理的描述指標來表示顆粒的破碎程度以及破碎后顆粒的相關性質.

然后,工程中顆粒材料破碎的計算效率問題: 從以上內容不難看出,目前的研究方法均存在計算效率問題,尤其是面向工程實際時,需要考慮的顆粒數量往往會達到百萬甚至千萬級,面對如此巨大數量的顆粒,如何保證計算效率是今后工作的重點,也是將顆粒材料破碎應用于工程的必要條件.

最后,顆粒破碎有效模擬的計算軟件問題: 面對機理研究以及工程應用,如何更有效地研究顆粒破碎過程,研發有效的計算軟件將是解決這一問題最為直接和有效的方法.因此,研發具有自主知識產權的模擬顆粒破碎的計算軟件,也將是今后工作的重點,當然,這也是難點.