基于模糊PI 的CVT 用電動油泵控制研究

支金澤，安穎，高帥

（湖南科技大學機電工程學院，湖南湘潭 411201）

0 前言

目前，以內燃機為動力的乘用車用CVT（Continuously Variable Transmission）的液壓油泵多采用發動機驅動的定量機械泵，CVT 控制、冷卻潤滑的流量壓力需求與油泵供油量之間存在“需求矛盾”，這種矛盾迫使油泵設計者需充分考慮油泵低轉速、CVT高流量需求的極限工況（例如，緊急制動工況和急加速工況），因此導致了CVT 油泵在正常行駛工況下的流量冗余、壓力冗余（溢流損失）及能耗增加。VAN DER SLUIS 等［1］研究表明，在NEDC 循環工況下，在發動機輸入CVT 的總功率中，液壓油泵的功率損失占比達到12%。

CVT 的流量需求分為兩部分：作動器所需要的高壓力部分，用于鋼帶夾緊；潤滑冷卻所需的低壓力部分，用于變矩器液力傳動、部件潤滑及系統散熱，這部分低壓流量需求僅需0.8 MPa 以內的壓力即可滿足。而上述傳統CVT 則充分兼顧極限工況將全部流量需求按照最高壓力需求供油。

為降低油泵的能量損耗，必須要降低溢流損失以實現按需供油，并隨著車輛的混動化，采用可控電動油泵作為CVT 供油源，實現發動機轉速與油泵供油流量的完全解耦是可采用方式之一［2-3］。在此種方案下，僅需通過改變油泵電機在CVT 不同運行工況下的轉速來滿足CVT 流量需求，而油壓也可在電機能力范圍內實現自動適應。由于永磁同步電機（Permanent Magnet Synchronization Motor，PMSM）具有體積小、可靠性高、能量密度高、能量轉換效率高等優點［4］，因此文中電動油泵選取永磁同步電機作為驅動，并進一步深入研究PMSM 的控制策略。

目前，許多研究人員和學者已經提出了多種PMSM 的控制策略。傳統PID 控制策略因易于實現且對硬件運算能力需求較小而得到了廣泛的應用，但是由于定參數對環境、工況的適應力較差，無法在全工況范圍內實現良好的動靜態調控特性［5-7］；模型預測控制依賴于模型精度，盡管對于復雜時變非線性系統的控制具有較大優勢，但該方法對模型參數變化較為敏感［8-9］；最大轉矩比電流控制通常以查表法實現，但由于數據量較大，系統的響應速度會受到嚴重影響［10-12］。鄒浙湘等［13］利用數學擬合以解耦控制電流分量，采用此方法的MTPA 控制算法對比查表法雖然提高了系統的響應速度，但仍具有很高的運算復雜程度。智能控制算法在永磁同步電機上的應用也相繼被提出：胡達等人［14］采用基于神經網絡的滑模控制，利用神經網絡的自主學習訓練在線調整滑模面的階次，有效提高了動態跟蹤性能并減小了穩態誤差，但神經網絡需要大量的訓練集且需要長時間學習才能提高精度。姜偉、喬林等人［15-16］應用遺傳算法于PMSM的控制系統中，利用遺傳算法尋優控制參數，提高了控制系統的抗干擾能力，但容易收斂于局部最優解。欲確保全工況范圍內PMSM 控制算法的控制品質，并為有效解決工程應用中的實時性與成本限制，陳文卓、劉宗鋒等［17-18］將模糊控制算法用于控制電機，充分利用了模糊控制解決非線性復雜系統的能力，有效地提高了響應速度和穩定性。可見，模糊控制算法用于控制電機具有兼顧設計難度、硬件成本和控制品質的應用潛力。因此，本文作者擬采用模糊PID 控制方法實現CVT 電動油泵的控制，并深入研究控制品質。首先在構建永磁電機數學模型的基礎上，加入了模糊PI 控制器，其次將CVT 油泵模塊加入到模型中，并進一步地在CVT 的緊急制動工況下仿真驗證了該控制算法的有效性和可行性。

1 PMSM 的數學模型

為了分析和求解PMSM 的數學模型，此處對電機做理想假設，即定子繞組感應電動勢呈正弦波，忽略渦流和遲滯損耗、鐵芯飽和效應［19］。

首先，為了實現電壓與電流的解耦，需要利用坐標變換。Clarke 變換是靜止坐標系變換，實現三相與兩相之間的轉換，亦稱為3S／2S 變換，具體關系如圖1 所示。

圖1 三坐標系關系Fig.1 Relation of three coordinates

按照幅值不變的變換規則，變量之間關系為

則反Clarke 變換為

其中：iA、iB、iC是電機三相定子電流；iα、iβ是α-β 坐標系的定子電流，此處物理量也可用電壓、磁鏈代替；T3s／2s為Clarke 變換矩陣，T2s／3s為反Clarke變換矩陣。

Park 變換是實現兩相靜止坐標系α-β 到兩相同步旋轉d-q 坐標系的轉化，反之亦是反Park 變換。具體如下：

則反Park 變換為

同理：T2s／2r、T2r／2s分別為Park、反Park 矩陣。經過以上兩種變換處理后，便可得到以下在d-q 坐標系下簡化、解耦的電壓方程：

磁鏈方程可表示為

電機電磁轉矩方程為

式中：ud、uq、Ld、Lq、ψd、ψq分別為d-q 坐標系下定子電壓、定子電感、定子磁鏈；Te為電磁轉矩；Pn為電機極對數；ψf為轉子永磁體產生的磁鏈；Rs為定子電阻；ωe為電角速度。

2 PMSM 矢量控制原理

2.1 矢量控制

矢量控制常用于解決交流電機的控制問題，其本質是解耦定子電流矢量，控制方式與他勵型直流電機相似，極大地簡化了電機的整個控制過程［5］。在電機的控制過程中，磁鏈和轉矩的大小受控于兩個電流分量，通過改變id、iq值的大小，便可完成電機轉速與轉矩的輸出。文中采用id＝0 控制，則式（7）可化簡為

該矢量控制基本結構如圖2 所示。從圖中可以看出其控制流程，控制系統實際電機轉速n和目標轉速nref的差值送入模糊PI 控制器，由于采用id＝0 矢量控制，便可得iqref，然后電流環PI 控制器計算目標值iqref與反饋值iq之差，便得到目標的直、交軸電壓ud和uq，再經Park、Clarke 逆變換和空間矢量脈寬調制（SVPWM）后，產生間隔120°電位角的三相正弦交流電以驅動永磁同步電機。

圖2 永磁同步電機矢量控制結構框圖Fig.2 Vector control structure block diagram of PMSM

2.2 空間矢量脈寬調制（SVPWM）

在電機調速過程中，其目標是產生一個理想的、標準的圓形旋轉磁場，從而帶動轉子轉動實現調速，而SVPWM 的主要功能就是產生近似圓形的旋轉磁場。SVPWM 技術的原理是利用特定的組合和序列信號來關斷和導通功率開關器件，使之產生三相正弦電壓作用于電機定子，以得到圓形旋轉磁場［20］。

按照逆變器功率器件開關狀態，可得到以下6 個非零電壓矢量U1（001）、U2（010）、U3（011）、U4（100）、U5（101）、U6（110）以及2 個零矢量U0（000）、U7（111），如圖3 所示。

圖3 電壓空間矢量圖Fig.3 Voltage space vector diagram

電壓空間矢量圖由8 個基本電壓矢量共同組成并六等分。每個扇區內電壓矢量都可由相鄰兩基本電壓矢量和零矢量作用一定時間合成，并且圓形區域為正常調制區域。

3 模糊PI 控制器的設計

模糊控制是基于模糊理論，根據專家知識和先驗實踐經驗制定模糊規則，對偏差量和偏差變化率進行實時調整，做出最優決策的智能控制方法［16］。它不依賴于精確模型，對于時變、非線性系統具有良好的控制效果和廣泛的適應性，且控制算法具有較高控制精度。模糊化、模糊推理以及解模糊化是模糊控制器的主要構成。文中的模糊PI 控制器是將模糊控制與PID控制相結合，利用模糊控制算法智能調節PI 參數，從而實現高精度控制。控制結構框圖如圖4 所示。

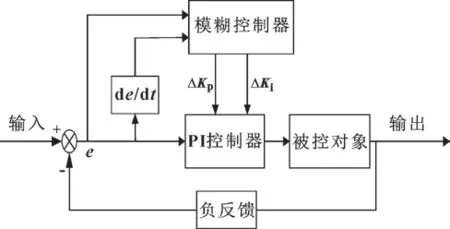
圖4 模糊PI 控制器結構框圖Fig.4 Structure block diagram of fuzzy PI controller

模糊PI 控制器將轉速目標值與反饋值做差并得到轉速誤差e，模糊控制器的輸入即為計算得到的誤差e和誤差偏差率ec，對輸入變量依次進行模糊處理、根據規則完成推理并將模糊變量數值化后，將比例系數增量ΔKp、積分系數增量ΔKi作為控制器的輸出，然后經PI 控制器完成參數累積，最終得到經過調整的PI 參數，從而實現對電機轉速的調節。經過調整后的PI 參數為

其中：Kp0、Ki0分別是PI 控制器的比例、積分系數初始值；ΔKp、ΔKi分別為比例、積分系數的修正值，經模糊推理得出。

3.1 模糊化

模糊化的定義是將精確的輸入變量數值轉化為與之對應的模糊的語言變量值。令｛NB（負大）、NM（負中）、NS（負小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）｝ 作為語言變量模糊集合。圖5 展示了變量的隸屬度函數，梯形函數分布在兩端，中間部分全為三角函數。輸入變量的論域相同，為［-5，5］；輸出變量ΔKp、ΔKi的論域分別為［-3，3］、［-1，1］。

圖5 輸入輸出變量隸屬度函數Fig.5 Membership functions of input and output variables

3.2 模糊規則的制訂與解模糊化

模糊控制器性能的好壞，關鍵在于模糊規則的制訂。ΔKp、ΔKi的模糊推理規則如表1 所示。

表1 ΔKp、ΔKi 的模糊規則Tab.1 Fuzzy rule of ΔKp，ΔKi

根據給出的模糊規則，在得到兩輸入變量的模糊集合后，采用Mamdani 推理方法，便能得到兩個輸出量的模糊集合。輸出量ΔKp、ΔKi與輸入量e和ec的關系如圖6 所示。

圖6 輸出量ΔKp（a）、ΔKi（b）的模糊規則面Fig.6 Fuzzy regular surfaces of outputs ΔKp（a），ΔKi（b）

經過模糊推理后的輸出量為模糊量，要進一步轉換為精確量以作用于控制參數，即解模糊化。在解模糊化過程中，本文作者采用加權平均法進行處理，具體公式為

式中：Ip、Ii分別為模糊推理輸出的比例、積分模糊變量；μ（Ip）和μ（Ii）分別對應Ip、Ii的隸屬度。

4 建模及仿真分析

4.1 永磁同步電機控制系統仿真分析

為驗證所設計的模糊控制算法應用于PMSM 的有效性，采用仿真方法，觀察在模糊控制的作用下，PI 控制參數自調整的有效性及其控制性能。被控電機參數如表2 所示。

表2 永磁同步電機參數Tab.2 Parameters of PMSM

在仿真過程中，兩種控制算法的電流環PI 控制器參數不隨時間變化，Kpd＝Kpq＝20，Kid＝Kiq＝2。傳統PI 控制器轉速環參數分別為Kp＝10，Ki＝1，并作為模糊PI 控制器的初始參數。設定當t＝0 s時，電機負載轉矩為0 N·m，電機轉速為1 000 r／min條件下使電機由靜止開始啟動，然后在t＝0.1 s 時突變負載為10 N·m，兩種算法的結果對比如圖7、8 所示。

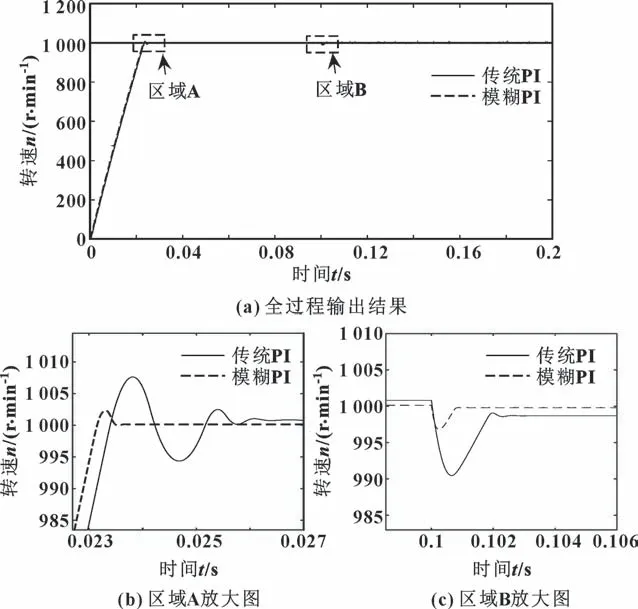
圖7 模糊PI 與傳統PI 轉速輸出結果對比Fig.7 Comparison of output speed between fuzzy PI and traditional PI：（a）output results of the whole process；（b）enlarged view of area A；（c）enlarged view of area B

圖8 模糊PI 與傳統PI 轉矩輸出結果對比Fig.8 Comparison of output torque between fuzzy PI and traditional PI：（a）output results of the whole process；（b）enlarged view of area A；（c）enlarged view of area B

由圖7、8 可知：在相同仿真環境下，輸出轉速在傳統PI 控制器作用下表現出較大的超調量，最高可達0.75%，且出現明顯的震蕩；在0.1 s 時刻負載突增時，轉速波動幅度較大，系統調節時間為2.5 ms，且存在明顯的穩態誤差。而在此基礎上，模糊PI 控制器的輸出轉速超調量小于0.2%，且負載突增時轉速波動幅度小，調節時間小于0.8 ms，轉矩響應迅速無抖動現象。因此，本文作者所設計的模糊PI控制器，在相同的初始參數條件下，有效地實現了對PI 參數的自調整，并改善了原PI 控制器的動靜態響應特性，能在目標轉速階躍及負載干擾中提升電機調速的動態響應速度、縮短調節時間并減少了穩態誤差，提升了系統的魯棒性和抗干擾性。

4.2 控制系統對電動油泵調速仿真分析

為驗證文中所提出的模糊PI 控制算法調節電動油泵的性能，選用車輛在緊急制動時CVT 所處極限工況下對電動油泵實際轉速需求作為控制目標。首先將CVT 液控系統的流量需求轉換為電動油泵的目標轉速，需構建流量與電機轉速的關系：

式中：n是電機轉速；ηE是泵的容積效率；V是油泵排量，為5 mL／r ；Q是電動油泵流量，在該工況下油泵所提供的流量主要由兩部分構成，包括由CVT 調速所需的流量Qshift和泄漏流量Qleakage。對于Qshift和Qleakage，有

其中：λ為帶輪錐角；As為從動油缸有效作用面積；di／dt為速比變化率；Rs為從動輪工作節圓半徑，可由速比計算得到；k為泄漏系數；p為工作壓力。根據上述公式可知，流量Q可由CVT 參數、速比和壓力計算得出。在實際過程中，由于存在能量損失，因此電機驅動功率與油泵輸出的液壓功率存在一定的效率轉換，具體如下：

式中：η為能量轉換效率，則驅動轉矩T為

對于CVT 油泵的流量供給來說，最苛刻的工況是緊急制動（Emergency Stop）。當CVT 運行在最小速比時，發動機轉速較低，而此時如果車輛出現緊急制動工況，那么在停車之前，液控系統要快速將金屬帶從最小速比控制到最大速比位置。選取實車測試中的某一緊急制動工況（初速度100 km／h，末速度為0）下，以最大強度制動，此時CVT 的速比回調速度如圖9 所示（2 s 左右從最小速比0.437 回位到最大速比2.623）。通過計算可得到該過程中所需的流量。利用式（11）（13）便可得電機的轉速與負載，將其作為系統的輸入信號。

圖9 緊急制動工況下測得的實驗數據Fig.9 Experimental datas measured under emergency stop condition：（a）speed ratio change；（b）volumetric efficiency of oil pump；（c）working pressure change；（d）flow change

綜合以上理論分析后，根據模塊化的建模思想，在MATLAB／Simulink 軟件中搭建如圖10 所示的電動油泵調速系統的仿真模型。將通過變換得到的轉速和負載轉矩作為系統的輸入，輸出結果如圖11、12 所示。

圖10 電動油泵調速系統仿真模型Fig.10 Simulation model of EOP speed control system

圖11 流量輸出結果 圖12 轉矩輸出結果Fig.11 Result of flow output Fig.12 Result of torque output

從圖11、12 中能夠看出：設計的控制系統能確保電動油泵輸出流量良好地滿足需求流量，電動油泵轉矩能根據外部負載轉矩做出快速響應并滿足轉矩要求，既保證了CVT 的正常工作，又極大程度上減少了溢流損失。說明設計的基于模糊PI 的控制算法適用于永磁同步電動油泵，且具有良好的控制性能，能滿足CVT 的供油需求。

5 結論

為實現一種兼具良好動靜態控制能力、具有工程化實用價值的油泵電機控制器，本文作者將模糊PI算法用于PMSM 油泵電機的控制。設計了模糊控制器，并利用仿真手段驗證了其對PI 參數自調整的有效性，進一步地將其應用于CVT 液控系統。結果表明：采用模糊PI 算法的控制系統，無論是在轉速階躍還是負載突變的情況下，其性能都優于傳統PI 控制系統，獲得了更好的動態響應和抗干擾性。同時，該算法能精準控制電動油泵的輸出流量，不僅能滿足CVT 正常工作的需求，而且有效減少了溢流損失。