非均勻磁場下Maxwell磁納米流體的拉伸流動與磁擴散分析

吳學珂, 劉春燕, 白 羽, 張 艷

(1. 北京建筑大學 理學院, 北京 100044;2. 建筑結構與環境修復功能材料北京市重點實驗室, 北京 100044)

0 引 言

聚合物是經聚合反應生成的高分子化合物,而熔融的聚合物在力的作用下可以流動,是一類同時具有黏性和彈性的黏彈性流體[1]．在聚合物中加入納米顆粒可有效改善聚合物的性能,提高其韌性和傳熱速率,在工業和生物醫學等領域被廣泛應用,增加了能源的利用率[2-3]．磁性納米顆粒具有磁性特征且具有納米顆粒的獨特效應,常見的磁性納米顆粒有金屬鐵、鈷、鎳、金屬氧化物Fe2O3和Fe3O4等,在熔融聚合物中加入微量的磁性納米顆粒,可以使材料的各種性能如導電性、導熱性、阻隔性等提高．Zainal等[4]應用邊界層理論研究了包含電磁流體動力學在拉伸板上復合納米流體的非穩態常駐點流動．Sheikholeslami等[5]研究了非均勻磁場對Fe3O4-水基納米流體強制對流換熱的影響．

對磁性納米流體施加外磁場,可以在非接觸的條件下對其流動產生影響．這種非接觸操控方式在實際操作中更便于實現,且操控范圍廣,不受pH值、離子強度、表面電荷和溫度的影響[6]．在多數實際情況下,外加磁場是可變的,近年來,很多研究探討了非均勻磁場對納米流體流動的影響．Sheikholeslami等[7]研究了變磁場下磁場力對納米流體傳熱的影響．Shaker等[8]研究了非均勻磁場對磁性納米流體在開腔通道內混合對流換熱的影響,發現腔加熱壁的上角附近產生了渦流．磁流體力學(MHD)是結合經典流體力學和電動力學的方法研究導電流體和磁場相互作用的學科[9],在天體物理、地球物理、宇航工程、電磁學以及工程技術中都有廣泛的應用．Bég等[10]研究了導電金屬流體在感應磁場作用下的流動,發現增加磁參數會使速度提高、感應磁場降低．Hayat等[11]采用有限差分格式數值計算了隨時間變化的黏性納米流體在感應磁場中的流動, 并討論了Brown運動和熱泳運動．但在現有的關于非均勻磁場的數值模擬研究中, 尚未清楚闡明感應磁場的物理機制．

考慮到黏彈性磁納米流體在流動過程中的復雜特性[12],將分數階導數引入本構關系能更靈活地描述黏彈性流體的性質．楊旭等[13]基于分數階微積分理論,采用空間分數階導數建立了圓管內分數階非Newton流體本構模型,為非Newton流體的記憶特征提供了一種建模方法．Zhao等[14]通過在本構關系中引入分數階Maxwell剪切應力和Cattaneo熱流模型,研究了Maxwell流體在平面上的非穩態Marangoni對流換熱．然而上述模型中分數階導數參數固定,導致了有限的記憶特性和非局部特性,且無法準確描述一些復雜的動力學過程,例如復合材料的流變特性[15]．分布階本構模型是分數階導數在參數值范圍內的積分,具有不同的時間和空間特征[16],作為更有效的工具引起了很多學者的關注．Yang等[17]建立了空間分布階本構關系來研究邊界層中的流動和傳熱．Long等[18]基于Maxwell流體流動和Cattaneo傳熱的傳統本構關系,建立了分布階導數的非穩態Marangoni對流邊界層流動和傳熱模型．Liu等[19]將分布階導數引入Maxwell流體的本構模型,并分析了相關參數的影響．

基于上述研究發現,在感應磁場作用下,非穩態時間分布階的Maxwell磁納米流體流動的問題很少有人研究．本文將時間分布階Maxwell本構關系代入動量方程,并與磁擴散方程建立流動和感應磁場的控制方程,然后結合有限差分方法與L1算法獲得控制方程的數值解,最后分析相關參數對流動和感應磁場的影響．

1 數 學 模 型

時間分布階Maxwell流體的本構方程為

(1)

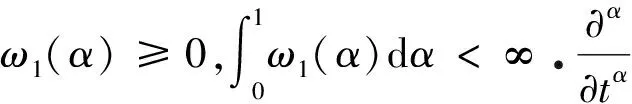
其中,Γ(·)為Gamma函數．

考慮線性拉伸板上的二維不可壓縮非穩態Maxwell磁納米流體的邊界層流動問題,如圖1所示．建立二維直角坐標系,其中x軸與平板平行,y軸垂直于平板．施加非均勻磁場He=H0(cos(x/L)+1),假設(u,v)和(H1,H2)分別是沿著板和垂直于板的速度和感應磁場的分量,并假設感應磁場的法向分量H2在壁處消失、平行分量H1在邊界層邊緣接近給定值．則時間分布階Maxwell磁納米流體的邊界層流動和磁擴散控制方程為

(2)

(3)

(4)

滿足下列初始條件和邊界條件：

(5)

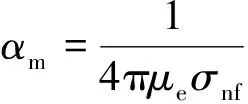
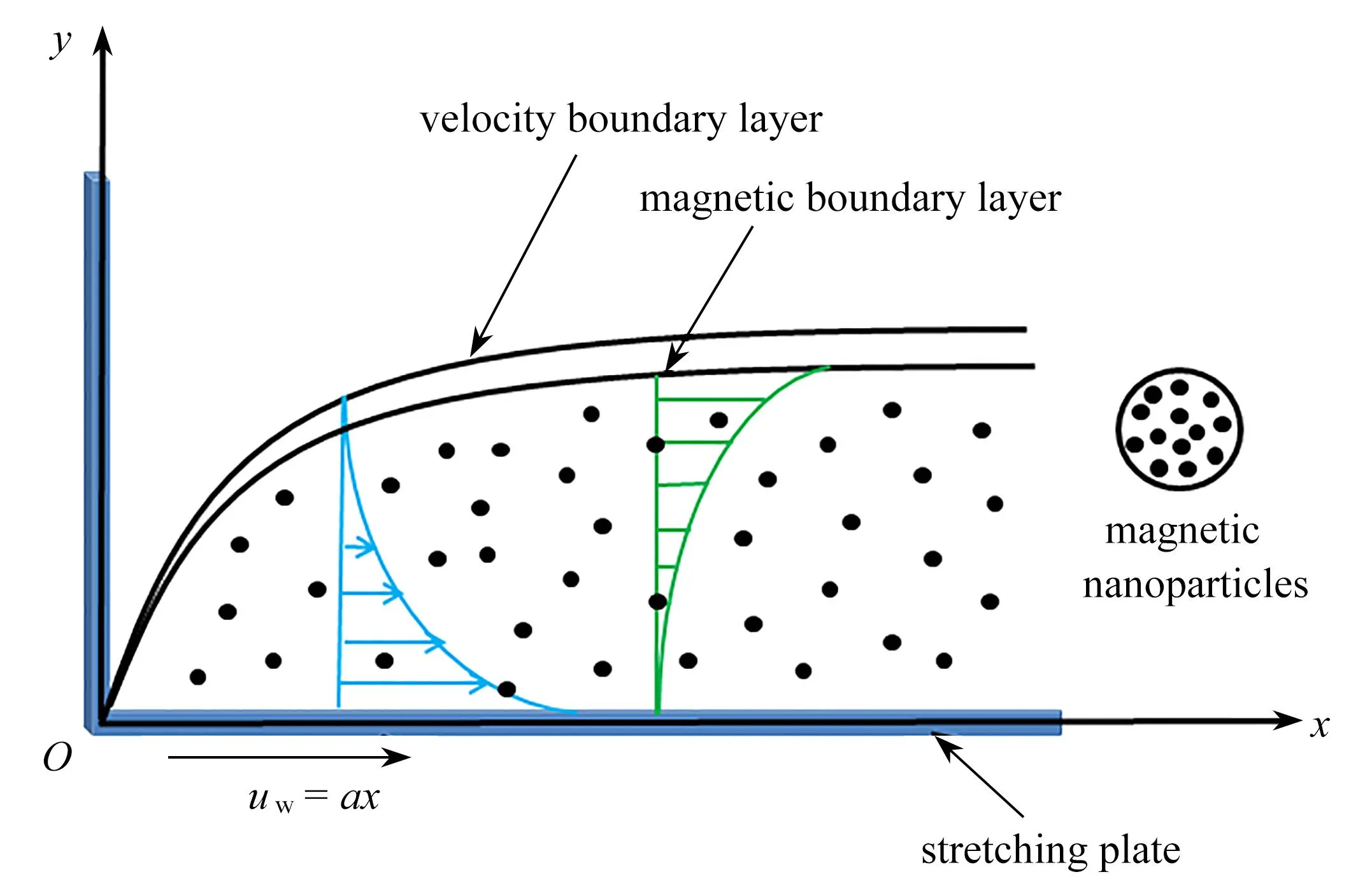
圖1 物理模型示意圖

納米流體的物理性質參數為

(6)

其中φ是磁性納米顆粒的體積分數,μf是流體的黏度,ρf和ρs分別是流體和磁性納米顆粒的密度,σf和σs分別是流體和磁性納米顆粒的電阻率．磁性納米顆粒鐵、鈷、Fe2O3和Fe3O4主要的物理性質如表1所示[21-22]．

表1 磁性納米顆粒的物理性質

對方程(2)—(5)進行無量綱化：

(7)

其中M是磁參數,Pr是磁Prandtl數,Re是Reynolds數,得到無量綱控制方程如下(為了方便,后面將省略標記“*”)：

(8)

(9)

(10)

無量綱化后的初值和邊界條件為

(11)

因此,建立了二維非穩態Maxwell磁納米流體的控制方程(8)—(11),方程(11)為相應的初始條件和邊界條件．

2 數值差分格式

采用有限差分法與L1算法[23]相結合來求解耦合的二維分布階控制方程(8)—(11)．對時間和空間進行網格劃分,設hx,hy分別為沿x軸和y軸的空間步長,τ為時間步長．定義

其中Mx,My,N是網格劃分的數量．

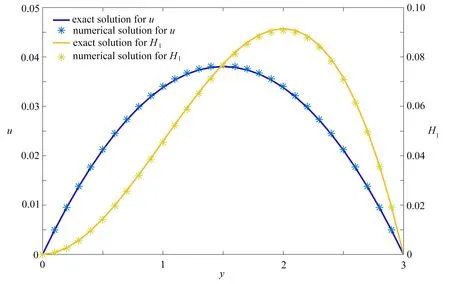
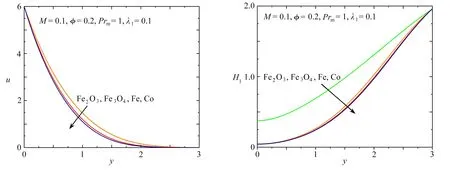
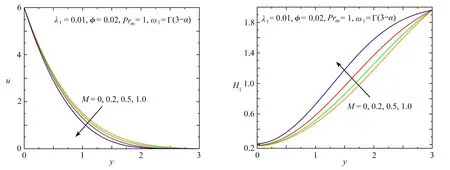
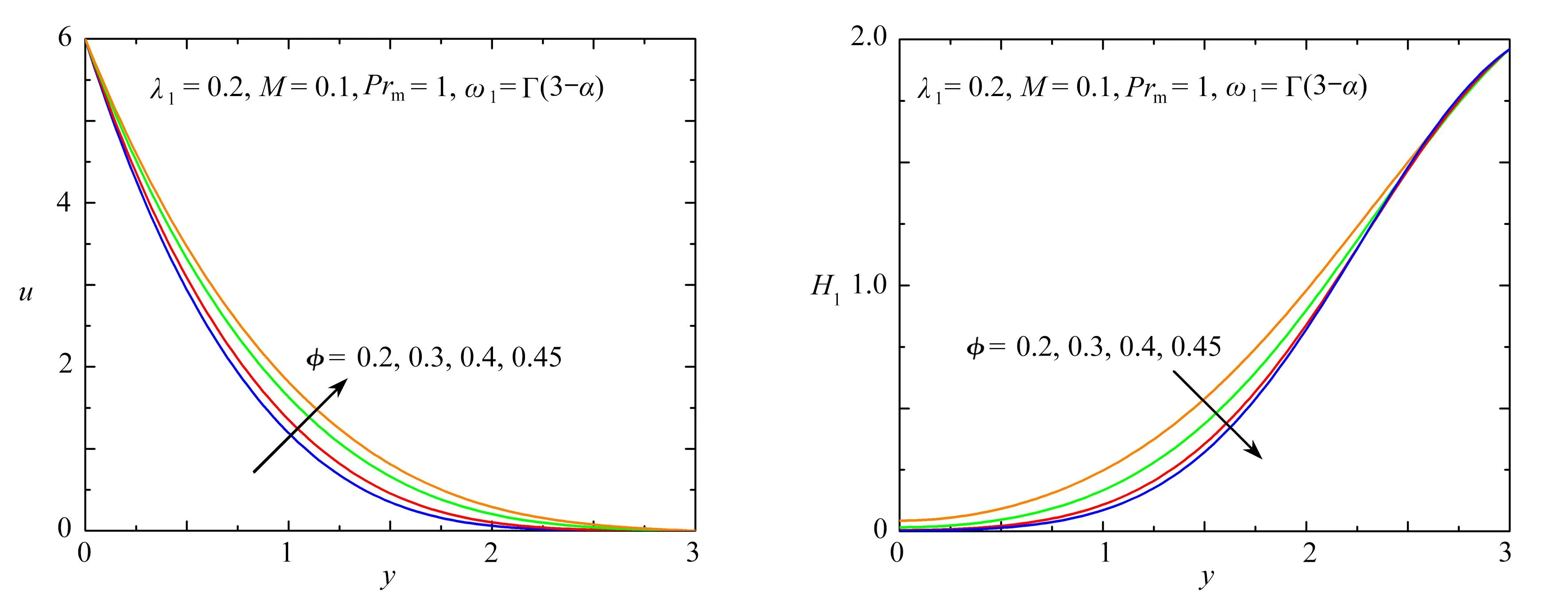
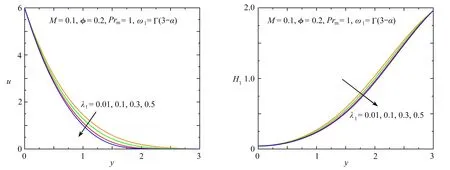
定理1 設0

稱之為L1算法,其基本思想是將被積函數中出現的f的分數階導數直接用數值微分公式逼近,還可改寫為

(12)

其中cj=(j+1)1-α-j1-α,j=0,1,2,…,N．

根據中點Gauss求積規則,使用多個分數項的加權和變換時間分布階分數導數,可以獲得分布項的數值離散格式：

(13)

對于離散區域[0,1]中αr階的時間分數階導數,利用定理1中的L1數值離散格式(13),可得到

(14)

(15)

其中

cr,0=1,cr,s=(s+1)1-αr-s1-αr,s=0,1,…,N．

將離散格式(12)、(14)和(15)代入控制方程(8)—(10)和初邊值條件(11),得到求解問題的數值差分格式．

3 結 果 分 析

利用第2節中的有限差分方法得到動量方程和磁擴散方程的數值解,并說明相關參數對速度和感應磁場的影響．構造解析解驗證了差分格式的收斂性,如圖2所示．

圖2 數值解和解析解的比較

圖3和圖4描繪了磁性納米顆粒Fe2O3、Fe3O4、Fe和Co對速度和感應磁場的影響．從圖3可以看出,密度相近的Fe2O3和Fe3O4納米顆粒對速度的影響幾乎相同,而密度最大的Co使流速受到最大限制,速度邊界層厚度最薄．從物理角度看,當磁性納米顆粒的體積分數相同時,密度越大,顆粒間的間隙越小,從而阻礙了流體的運動．圖4表明,添加的Fe2O3納米顆粒電阻率最小,則感應磁場最大,磁邊界層厚度最厚;對于電阻率相近的Fe和Co,感應磁場的分布幾乎相同．由于磁性納米顆粒的電阻率與電導率呈反比,所以當電阻率增大時,感應磁場減小．

圖5和圖6為變化的磁參數M對Fe3O4納米流體速度和感應磁場的影響．圖5中的曲線表明流動的模式一致,流速值隨著磁參數的增加而降低．在非均勻磁場作用下,邊界層內產生與流體運動方向相反的磁場力,所以當M>0時,磁場力對流體的速度起抑制作用,使得邊界層厚度變薄．當M=0時,無磁場力,Fe3O4納米流體速度由于內摩擦阻力作用逐漸減小．如圖6所示,在邊界層內感應磁場隨M的增大而增大．因為M增大時磁導率增加,磁擴散效應顯著,從而感應磁場增加．

圖3 不同磁性納米顆粒對速度的影響

圖5 不同M對速度的影響

圖7和圖8顯示了速度和感應磁場隨磁性納米顆粒Fe3O4體積分數φ的變化．當φ增加時,速度增大,邊界層厚度變厚,感應磁場減小．由于拉伸板的運動導致固體顆粒運動增加,從而速度隨著磁納米顆粒的加入而增加．而在外加磁場的作用下,隨著φ的增加,速度的增大導致磁對流項增大,使得磁擴散效應減小,從而在邊界層內感應磁場減小．圖9和圖10顯示了松弛時間參數λ1對Fe3O4納米流體中速度和感應磁場的影響．當選擇權重系數ω1(α) =Γ(3-α),無量綱時間t=1時,可以觀察到λ1越大,速度和感應磁場越小,這是由于流體的黏性增加,阻礙了流體的運動進而導致磁場減小,這和應力松弛現象是一致的．

圖7 不同φ對速度的影響

圖9 不同λ1對速度的影響

4 結 論

磁性納米顆粒可以改善聚合物的性能,線性拉伸板上非穩態流動與磁擴散的研究為其提供了良好的理論基礎．本文利用分布階本構模型,研究了黏彈性基磁納米流體在非均勻磁場下的二維不可壓縮邊界層流動,并考慮了高Reynolds數下的感應磁場分布．將時間分布階Maxwell方程引入動量方程,建立了速度和磁擴散控制方程組．使用有限差分法和L1算法耦合求解偏微分方程組的數值解,并驗證了收斂性,結合圖像分析了相關物理參數對速度和感應磁場的影響．所得主要結論如下：Maxwell流體的速度和感應磁場在添加Fe2O3納米顆粒時達到最大,此時速度邊界層和磁邊界層的厚度最厚;由于磁場力的影響,增大的磁參數阻礙了流體的運動,增強了磁擴散;隨著Fe3O4納米流體體積分數增加,速度增大,感應磁場減小;此外,較高的松弛時間參數會使Maxwell流體的流動和磁場的擴散減弱．因此,本文從數值解的角度研究了添加磁性納米顆粒的熔融聚合物在非均勻磁場下的邊界層拉伸流動與磁擴散,對制備出高性能的聚合物材料具有重要意義．

致謝本文作者衷心感謝北京建筑大學金字塔人才培養工程項目(JDYC20220829)、北京建筑大學促進高校內涵發展定額項目(X21027)和北京建筑大學研究生創新項目(PG2023144)對本文的資助．