找準(zhǔn)目標(biāo)切入，分類討論引領(lǐng)

■陳渭渭

分類討論思想是高考數(shù)學(xué)中經(jīng)常用到的基本數(shù)學(xué)思想方法之一,滲透于數(shù)學(xué)問題的方方面面。利用分類討論思想解決問題的關(guān)鍵是找準(zhǔn)切入目標(biāo),合理分類,實(shí)現(xiàn)問題的圓滿解決。

一、根據(jù)概念、法則、公式進(jìn)行分類討論

例1 (2023 年新高考卷)設(shè)集合A={0,-a},B={1,a-2,2a-2},若A?B,則a=( )。

分析:從兩集合間的包含關(guān)系入手,分析集合間元素的關(guān)系,構(gòu)建相應(yīng)的方程,結(jié)合方程所對應(yīng)的參數(shù)值進(jìn)行分類討論求解。

解:由A?B,結(jié)合兩集合之間元素的關(guān)系得a-2=0或2a-2=0。

當(dāng)a-2=0時(shí),解得a=2,此時(shí)A={0,-2},B={1,0,2},不滿足條件A?B,舍去;

當(dāng)2a-2=0 時(shí),解得a=1,此時(shí)A={0,-1},B={1,-1,0},滿足條件A?B。

綜上可得,a=1。應(yīng)選B。

題中兩集合之間的包含關(guān)系就是分類討論解決問題的基礎(chǔ)條件,要注意問題的切入視角與應(yīng)用方式,不要出現(xiàn)重復(fù)或遺漏。

二、利用參數(shù)的取值、變量的變化進(jìn)行分類討論

例2 關(guān)于x的不等式mx2-mx+m+1>0 恒成立,則實(shí)數(shù)m的取值范圍為( )。

A.(0,+∞)

B.[0,+∞)

分析:利用不等式恒成立,對二次項(xiàng)系數(shù)進(jìn)行分類討論,借助二次函數(shù)的圖像與性質(zhì)進(jìn)行求解。

解:關(guān)于x的不等式mx2-mx+m+1>0恒成立,以下分兩種情況進(jìn)行討論。

當(dāng)m=0時(shí),可得1>0,適合題意;

當(dāng)m≠0時(shí),由mx2-mx+m+1>0恒成立得解得m>0。

綜上可得,m≥0,即實(shí)數(shù)m的取值范圍為[0,+∞)。應(yīng)選B。

解決一些含參數(shù)的不等式問題,往往離不開參數(shù)的取值范圍或限制條件,對參數(shù)進(jìn)行合理的分類討論是解題的關(guān)鍵。

三、結(jié)合圖形的位置、形狀進(jìn)行分類討論

例3 (2023年高考上海卷)已知a∈R,記y=sinx在[a,2a]上的最小值為sa,在[2a,3a]上的最小值為ta,則下列情況不可能的是( )。

A.sa>0,ta>0 B.sa<0,ta<0

C.sa>0,ta<0 D.sa<0,ta>0

分析:根據(jù)正弦函數(shù)的圖像,利用參數(shù)a和對應(yīng)區(qū)間上的最值,結(jié)合特殊值的選取進(jìn)行分類討論,進(jìn)而判斷三角函數(shù)在給定區(qū)間上的最小值的正負(fù)情況。

解:依題中給出的區(qū)間,可知a>0,區(qū)間[a,2a]與區(qū)間[2a,3a]相鄰,且區(qū)間長度相同,畫出函數(shù)y=sinx的部分圖像,如圖1所示。

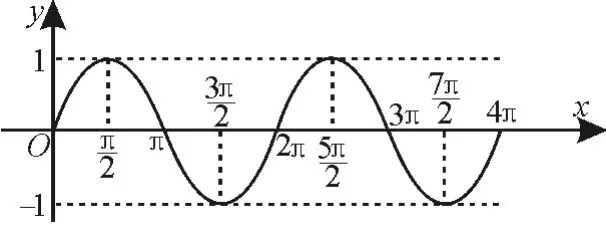
圖1

綜上可知,不可能成立的是sa<0,ta>0。應(yīng)選D。

本題是利用三角函數(shù)的圖像,結(jié)合參數(shù)的特殊取值進(jìn)行分類討論求解的。

四、利用運(yùn)算結(jié)果、性質(zhì)進(jìn)行分類討論

例4 若函數(shù)f(x)=logax(a>0,且a≠1)在區(qū)間上的最大值為2,最小值為m,函數(shù)g(x)=(3+2m)x在區(qū)間[0,+∞)上是增函數(shù),則a+m=____。

分析:利用對數(shù)函數(shù)的基本性質(zhì),對底數(shù)a的兩種不同取值進(jìn)行分類討論,結(jié)合函數(shù)在給定區(qū)間上的最值構(gòu)建關(guān)系式,確定對應(yīng)的參數(shù)值。

解:結(jié)合對數(shù)函數(shù)的基本性質(zhì),分以下兩種情況進(jìn)行討論。

當(dāng)a>1時(shí),函數(shù)f(x)=logax是正實(shí)數(shù)集上的增函數(shù),而函數(shù)f(x)=logax在區(qū)間上的最大值為2,所以f(4)=loga4=2,解得a=2,所以,此時(shí)g(x)=x在區(qū)間[0,+∞)上是增函數(shù),符合題意,所以a+m=2-1=1。

當(dāng)0

綜上可得,a+m=1。

本題是利用對數(shù)函數(shù)的底數(shù)a的兩種不同取值情況,結(jié)合對應(yīng)函數(shù)的單調(diào)性求解的。

1.若命題“?x∈R,x2-4x+a≠0”為假命題,則實(shí)數(shù)a的取值范圍是( )。

A.(- ∞,4] B.(- ∞,4)

C.(-∞,-4) D.[-4,+∞)

提示:因?yàn)槊}“?x∈R,x2-4x+a≠0”為假命題,所以“?x0∈R,x20-4x0+a=0”是真命題,所以方程x2-4x+a=0 有實(shí)根,所以Δ=(-4)2-4a≥0,解得a≤4。應(yīng)選A。

2.若命題“?x∈R,(a2-3a+2)x2+(a-1)x+2<0”是真命題,則實(shí)數(shù)a的取值范圍為_____。

提示:①若a2-3a+2=0,則a=1或a=2。當(dāng)a=1 時(shí),不等式為2<0,顯然不成立;當(dāng)a=2時(shí),不等式為x+2<0,顯然?x∈R,使x+2<0 成 立,即a=2 符 合 題 意。②若a2-3a+2<0,則10,則a<1或a>2,此時(shí)不等式對應(yīng)的一元二次函數(shù)的圖像開口向上,要使其符合題意,只需方程(a2-3a+2)x2+(a-1)x+2=0 有兩個(gè)不相等的實(shí)根,所以Δ=(a-1)2-4×2(a2-3a+2)>0,解得,所以

由①②③得實(shí)數(shù)a的取值范圍為1<,即