溫度突變下人體熱反應的實驗研究*

張子揚 趙勝凱 武 峰 翟永超△

(1.綠色建筑全國重點實驗室,西安;2.西安建筑科技大學,西安)

0 引言

生活中人們經常經歷環境溫度發生突變的情況,如出入地鐵站和辦公樓等。探索人體在溫度突變環境下的熱反應規律,是合理設計建筑物室內外溫差和過渡空間溫度參數及開發人體熱感覺預測模型的基礎。

為探索人體在溫度突變動態環境中的生理響應及其與主觀感覺變化的關系,國內外學者通過在實驗室營造不同的溫度工況,開展了諸多人體熱舒適實驗研究。Stolwijk等人通過實驗探索了人體在經歷28 ℃→33/38/43/48 ℃→28 ℃往返式溫度突變時皮膚溫度、出汗量、熱負荷、皮膚蒸發熱損失的變化規律,發現在33 ℃和38 ℃工況下皮膚蒸發熱損失和皮膚溫度之間有很好的相關性[1]。Gagge等人[2]、Dear等人[3]、Nagano等人[4]、Tsutsumi等人[5]、Zhao等人[6]和Liu等人[7]開展了一系列中性→冷(熱)和冷→熱的溫度突變實驗后發現了3條重要規律:1) 在溫度突變的情況下,人體產生心理超前現象,表現為熱感覺等心理反應變化超前于皮膚溫度的變化;2) 突變瞬間人體出現熱感覺超越現象,表現為環境溫度突升或突降時,熱感覺的初始反應非常強烈,而后逐漸減弱至穩態水平;3) 人體進入低溫環境時皮膚溫度變化幅度大,穩定時間長,生理熱調節遲鈍,而進入高溫環境時相反。此外,Zhang等人在中性→熱(冷)→中性往返式溫度突變實驗中發現前后2次在中性環境中的熱感覺投票值不同,表現為經歷過低溫突變后熱感覺投票升高,經歷過高溫突變后熱感覺投票降低,即出現熱感覺不對稱現象[8]。廖建科在熱→中性→熱往返式溫度突變實驗中也發現了該現象[9]。已有的關于人體在溫度突變環境中熱反應的研究大都集中于中小溫差突變,而人們在生活中經常經歷一些溫差達到20 ℃以上的短時溫度突變,而且已有的實驗結果局限于皮膚溫度、皮膚濕潤度和主觀反應,缺少在溫度突變環境下人體與環境的換熱和熱負荷規律的探索。

基于實驗研究,國內外學者提出了人體熱感覺預測模型,主要有2種:1) 直接建立人體熱感覺和環境參數的關系,比如Fanger提出的PMV模型[10],這種模型多適用于穩態環境。2) 量化熱感覺與生理指標之間的關系,如Wang等人將動態環境中的熱感覺分為穩態項和動態項,其中穩態項與皮膚溫度呈線性關系,并進一步提出了動態熱感覺模型[11];張宇峰等人發現動態項隨皮膚溫度變化率的變化而變化[12];Arens等人認為人體熱感覺除了受皮膚溫度影響外,還受核心溫度的影響[13];Zhang等人對人體13個部位建立了局部熱感覺回歸模型,并在模型中增加了核心溫度[14];Fiala模型[15]中的動態項也考慮了核心溫度的影響,采用核心溫度對熱中性狀態的偏離量作為變量。

綜上,本文的主要研究目的為:1) 在人工氣候室開展高溫和低溫突變的人體熱舒適實驗,獲得不同突變溫差、突變方向下人體皮膚溫度、皮膚濕潤度隨環境溫度及暴露時間的變化規律,并進一步利用人體熱平衡方程計算實驗過程中的人體熱負荷,探索人體生理調節規律;2) 分析人體皮膚溫度和主觀熱感覺之間的關系,建立基于皮膚溫度及其變化率的熱感覺預測模型;3) 探索溫度突變環境中人體熱感覺與人體熱負荷、皮膚溫度之間的關系,從而為動態環境下熱感覺的預測和評價提供參考。

1 研究方法

1.1 實驗平臺

實驗在西安建筑科技大學人工氣候室進行,實驗室由2個可單獨調控的房間(A室和B室)組成,A室尺寸為4.5 m(長)×3.9 m(寬)×2.6 m(高),B室尺寸為3.0 m(長)×2.4 m(寬)×2.1 m(高),A室和B室之間由凈寬800 mm的保溫密封門連通,2個房間之間裝有1 510 mm×1 100 mm的雙層真空玻璃窗。人工氣候室的空氣經空調機組壓縮、加濕、變溫等處理后,從上送風口和帶孔板的吊頂送入室內,由下回風口及帶孔板的架空地板回風,形成通風循環,確保了A室和B室的室內熱環境參數分布均勻。其性能指標如下:A室和B室空氣溫度控制精度為±0.3 ℃,相對濕度控制精度為±5%;送風量在設計送風量的50%～100%之間可調。以上的性能指標在一定程度上確保精確營造穩定均勻的室內環境。實驗中人工氣候室的布置情況見圖1。

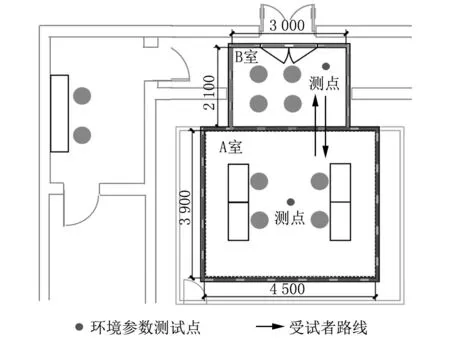
圖1 人工氣候室布置

1.2 受試者

招募24名身體健康的受試者,其中男生和女生各12名,均為西安建筑科技大學在校學生,受試者基本信息見表1。受試者在實驗過程中穿著統一服裝,根據ISO 7730:2005[16],夏季工況服裝熱阻為0.57 clo(短袖T恤、長褲、運動鞋),過渡季工況服裝熱阻為0.7 clo(長袖襯衫、短袖T恤、長褲、運動鞋),冬季工況服裝熱阻為1.8 clo(長袖襯衫、厚外套、短款羽絨服、秋褲、長褲、運動鞋)。

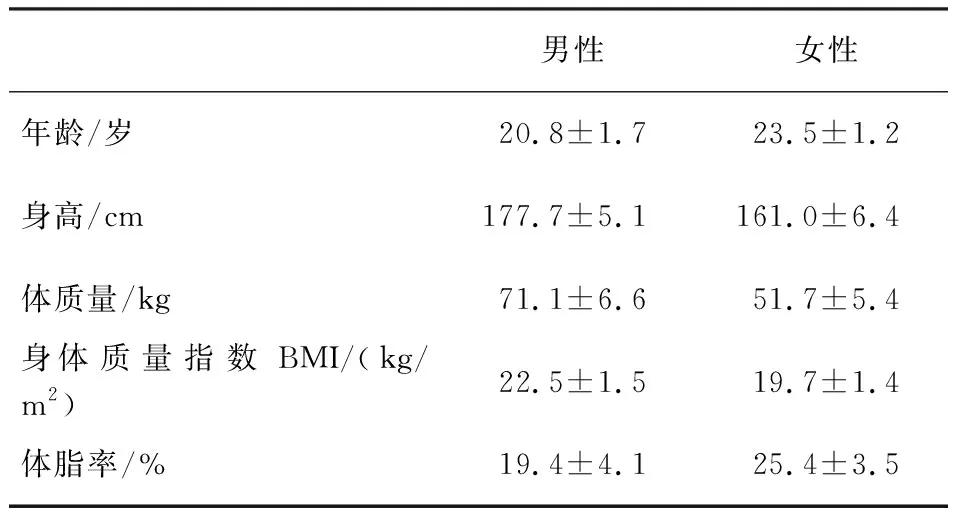
表1 受試者詳細信息

1.3 相關參數及測量

1.3.1環境參數測量方法

實驗期間測量的環境參數為空氣溫度、相對濕度、氣流速度及黑球溫度,測量儀器見表2。測量位置為A、B室內0.1、0.6、1.1 m高度處。

表2 環境參數測量儀器

1.3.2生理參數測量方法

本研究測試了與人體熱舒適相關的生理參數:皮膚溫度、皮膚濕潤度。測量儀器見表3。

表3 生理參數測量儀器及測量位置

1.3.3生理參數計算方法

皮膚溫度:利用熱電偶對身體16個部位的皮膚溫度進行連續測量,采用其中7個部位的皮膚溫度計算平均皮膚溫度,計算式為[17]

tsk,m=0.07tfh+0.35tp+0.14tla+

0.05tlh+0.19tlt+0.13tll+0.07tlf

(1)

式中tsk,m為平均皮膚溫度,℃;tfh為前額皮膚溫度,℃;tp為骨盆皮膚溫度,℃;tla為左小臂皮膚溫度,℃;tlh為左手皮膚溫度,℃;tlt為左大腿皮膚溫度,℃;tll為左小腿皮膚溫度,℃;tlf為左腳皮膚溫度,℃。

皮膚濕潤度:將iButton溫濕度傳感器布置在受試者的4個部位以采集皮膚與服裝之間空氣間層的溫度和皮膚表面相對濕度數據,溫濕度傳感器與皮膚表面間隔0.3 cm,以確保測量部位的汗液能夠正常蒸發。皮膚濕潤度計算式如下[18]:

w=0.3wch+0.3wa+0.2wt+0.2wl

(2)

式中w為全身皮膚濕潤度;wch為左前胸皮膚濕潤度;wa為左上臂皮膚濕潤度;wt為左大腿皮膚濕潤度;wl為左小腿皮膚濕潤度。

人體熱負荷:根據人體熱平衡方程[19],環境中人體的熱負荷LT可以表示為

LT=M-W-R-C-Esk-Cres-Eres

(3)

式中M為靜坐狀態的代謝率,W/m2,取60 W/m2;W為對外做功,W/m2,在本實驗中取0 W/m2;R為輻射換熱量,W/m2;C為對流換熱量,W/m2;Esk為皮膚蒸發散熱量,W/m2;Cres和Eres分別為來自呼吸顯熱和潛熱的散熱量,W/m2。

R=3.96×10-8fcl[(tcl+273)4-(ta+273)4]

(4)

C=hcfcl(tcl-ta)

(5)

(6)

Cres=0.001 4M(34-ta)

(7)

Eres=1.7×10-5M(5 867-pa)

(8)

式(4)～(8)中fcl為服裝面積因子,fcl=1.00+0.28Icl(其中Icl為服裝熱阻,clo,1 clo=0.155 m2·℃/W);tcl為服裝表面溫度,℃;ta為空氣溫度,℃;hc為對流換熱系數,W/(m2·K),hc=2.38(tsk-ta)0.25,其中tsk為皮膚表面溫度,℃;psk,s為平均皮膚溫度對應的飽和水蒸氣分壓力,Pa;pa為環境空氣中的水蒸氣分壓力,Pa;Re,cl為服裝的蒸發熱阻,m2·Pa/W,Re,cl=Rcl/0.005 61,其中Rcl為服裝熱阻,m2·℃/W;he為蒸發傳熱系數,W/(m2·Pa),he=0.016 5hc。

1.3.4主觀熱感覺調查

采用問卷調查受試者的主觀熱感覺。問卷包括受試者對熱環境的全身和局部的主觀感受,包括熱感覺、熱舒適等問題。熱感覺投票采用ASHRAE標準中的9級連續標尺:-4非常冷、-3 冷、-2涼、-1稍涼、0不冷不熱、1稍暖、2暖、3熱、4非常熱。熱舒適投票為斷裂標尺,不舒適的投票范圍從“-4非常不舒服”到“-0.01有點不舒服”,舒適的投票范圍從“0.01有點舒服”到“4非常舒服”。

1.4 實驗控制及工況

通過人工氣候室完成不同的溫度突變過程,A室模擬不同季節的中性溫度,B室模擬不同工況下的高溫和低溫條件。實驗包括9種不同溫度的工況,各工況A、B室溫度設定值見表4。每次實驗完成1個工況,夏季工況模擬受試者在夏季經歷短時高溫環境后進入中性環境的場景;過渡季工況模擬受試者在過渡季經歷短時偏涼環境后進入中性環境的場景,冬季工況模擬受試者在冬季經歷短時寒冷環境后進入中性環境的場景。A、B室的相對濕度均控制在50%,空氣流速控制在0.05 m/s以內,平均輻射溫度近似于空氣溫度。

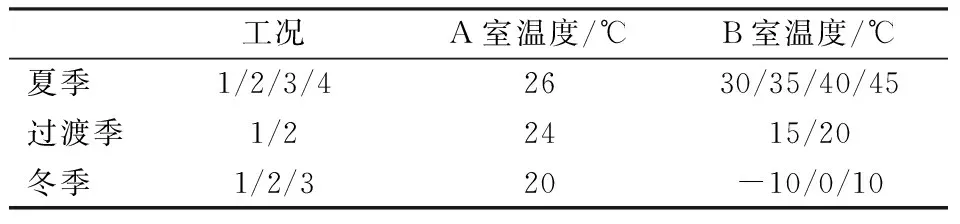
表4 實驗工況設計

1.5 實驗步驟

實驗時間為2020年9月和12月,2021年3月和5月。實驗開始前,受試者更換統一服裝,固定測量皮膚溫度的熱電耦及測量皮膚濕潤度的紐扣。實驗流程如圖2所示,第1階段受試者在A室中預暴露30 min,第2階段進入B室停留15 min,第3階段再進入A室中靜坐40 min。整個實驗過程中連續測量皮膚溫度、皮膚濕潤度及環境參數。

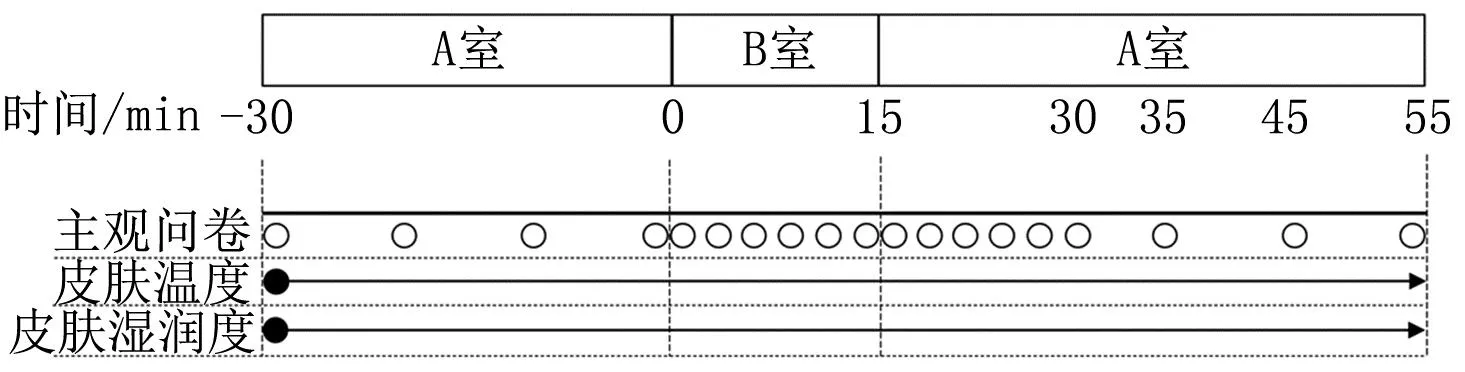
注:○表示主觀問卷記錄時刻。圖2 實驗流程

2 實驗結果

2.1 生理反應

圖3顯示了各工況下受試者平均皮膚溫度隨時間的變化規律。可以看出:在預暴露后期皮膚溫度處于穩定狀態;在進入低溫或高溫環境時,突降或突升溫差越大,受試者的平均皮膚溫度降低或升高越顯著;突變溫差越大,受試者的皮膚溫度在返回中性溫度環境后達到穩定的時間越長;在夏季各工況下,受試者由偏熱環境回到中性溫度環境時,平均皮膚溫度均在較短時間內(約5 min)迅速降低并逐漸趨于穩定;而冬季和過渡季各工況下,受試者由偏冷環境回到中性溫度環境時,平均皮膚溫度升高緩慢,這表明人體皮膚溫度對冷刺激的調節快于熱刺激的響應。對比溫度突變前后中性溫度下受試者的平均皮膚溫度,當突變溫差Δt≤4 ℃時,受試者皮膚溫度在第3階段結束時近似等于第1階段的皮膚溫度,表明該溫差范圍內人員能較好地響應溫度調節,并在短時間內恢復自身熱平衡。當突變溫差Δt≥9 ℃時,突變前后皮膚溫度出現一定的不對稱性。這與以往的研究結果一致[7,20]。

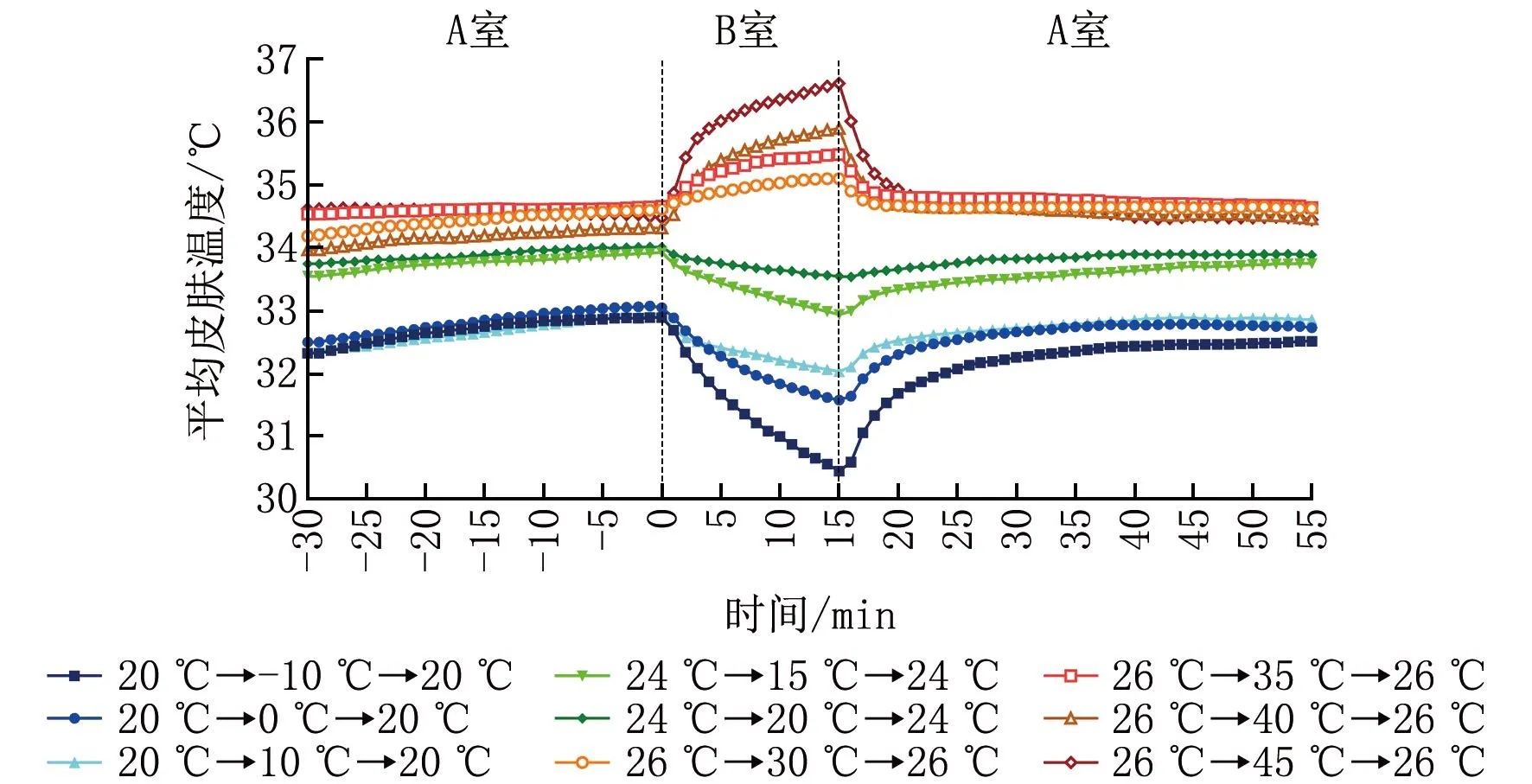
圖3 各工況下受試者平均皮膚溫度的逐時變化

由于本次實驗中受試者只有在夏季工況下存在出汗行為,故僅對夏季各工況下皮膚濕潤度測量結果進行分析,結果如圖4所示。可以看出:在預暴露過程中受試者的皮膚濕潤度均能達到穩定;受試者進入高溫環境后人體體溫調節系統發揮作用,出汗量迅速增加以促進皮膚蒸發散熱,且增加的幅度隨突變溫差的增大而增大;在回到中性環境后皮膚濕潤度逐漸降低,但一直到實驗結束仍未恢復至經歷高溫突變前的水平。

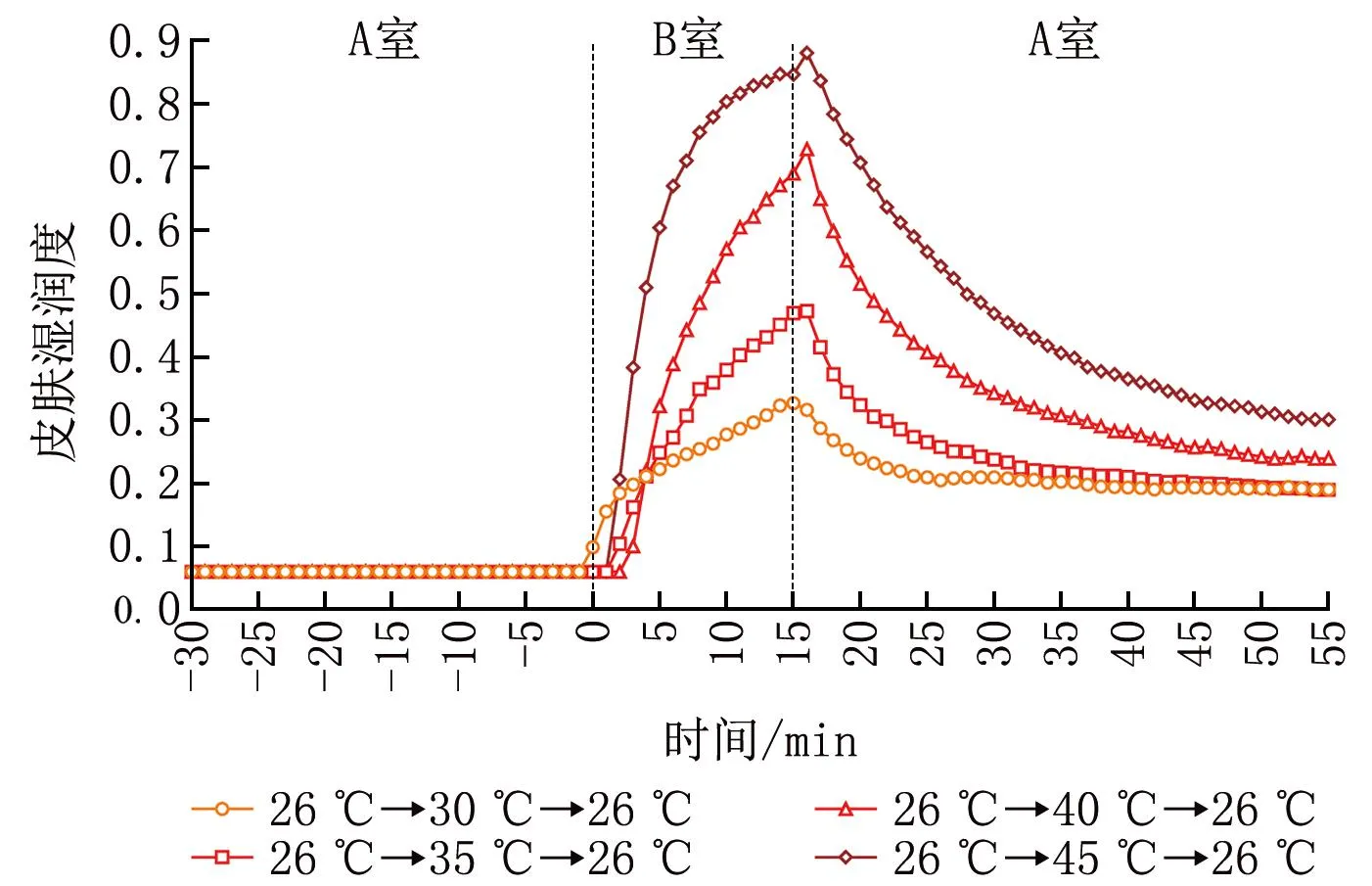
圖4 夏季各工況下受試者皮膚濕潤度的逐時變化

2.2 主觀反應

圖5顯示了各工況下受試者全身熱感覺的逐時變化情況。可以看出:過渡季和冬季各工況下,受試者由中性溫度環境進入低溫環境的瞬間熱感覺下降幅度隨突變溫差的增大而增大,在低溫環境中受試者的熱感覺不斷降低,當受試者重新回到中性溫度環境時,熱感覺恢復至突變前的水平并趨于穩定;夏季各工況下,受試者由中性溫度環境進入高溫環境的瞬間熱感覺上升幅度隨突變溫差的增大而增大,熱感覺投票值隨暴露時間的延長不斷提高,當受試者重新回到中性溫度環境時,暴露初始時刻熱感覺投票值降低至負值,出現明顯的“冷感超越”現象,在發生降溫突變的前2 min內“超越”現象最明顯,且該“超越”現象隨著突變溫差的增大顯得更明顯。對比夏季各工況前后2次在中性溫度環境中的熱感覺投票值,發現經歷過高溫突變后熱感覺投票值降低,出現熱感覺不對稱現象。Zhang等人[8]和Ji等人[21]對這種不對稱現象的解釋是:在熱感覺達到穩定后,皮膚溫度還在繼續變化,而此時的皮膚溫度變化率對熱感覺的影響大于皮膚溫度,使得熱感覺繼續變化,偏離中性條件下的熱感覺投票值。

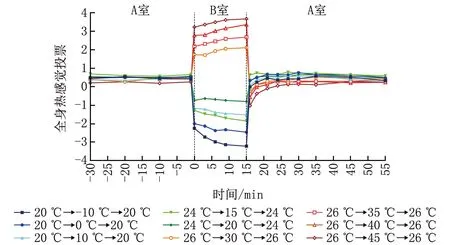
圖5 各工況下受試者全身熱感覺的逐時變化

圖6顯示了各工況下受試者全身熱舒適的逐時變化情況。可以看出:各工況預暴露過程中受試者熱舒適投票值基本在1.5以上,經歷溫度突降或突升的初始時刻,熱舒適投票值迅速降低,且突變溫差越大,其熱舒適投票值越低;隨著暴露時間的延長,-10 ℃和45 ℃環境中的熱舒適投票值由初始時刻的-2降低到-3以下,其余工況的熱舒適投票值也降低了超過0.5,這可能是由于受試者的熱負荷或冷負荷隨著暴露時間的延長而增大,導致其熱舒適水平持續降低;第3階段初始時刻的熱舒適投票值均低于第1階段,且這種差異在20 ℃→-10 ℃→20 ℃和26 ℃→45 ℃→26 ℃工況下最明顯,這可能是由于這2種工況的突變溫差過大,導致受試者需要更長的時間去適應;在各突變工況下,主觀反應變化均超前于生理反應,即出現心理超前現象。

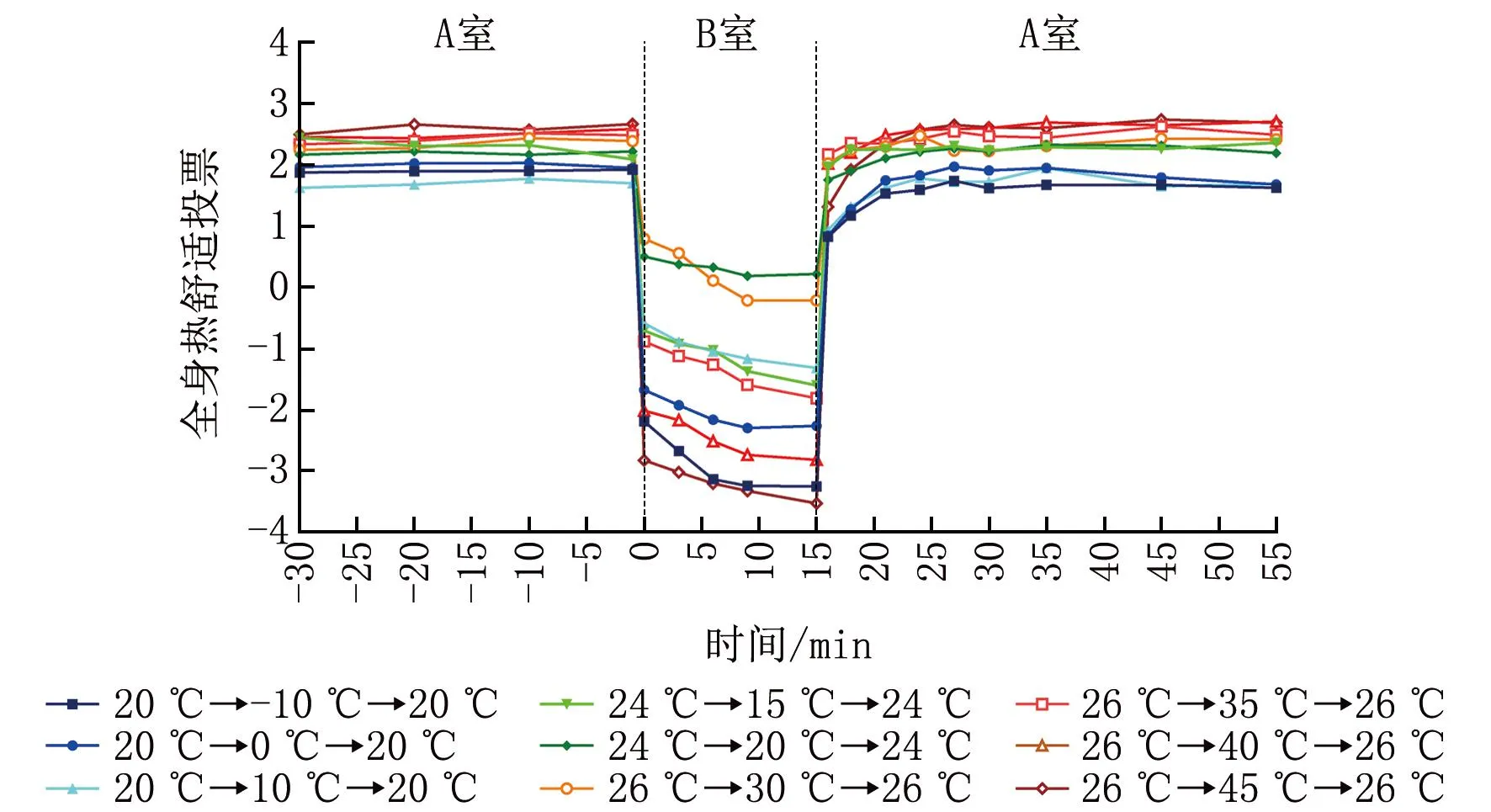
圖6 各工況下受試者全身熱舒適的逐時變化

2.3 全身熱負荷

圖7顯示了各工況下受試者全身熱負荷隨時間的變化規律。可以看出:在預暴露過程中,受試者的全身熱負荷穩定在0～10 W/m2之間;夏季工況下受試者進入高溫環境的初始時刻,由于空氣溫度和平均輻射溫度均高于皮膚溫度,所以全身熱負荷劇增,且突變溫差越大熱負荷增加越多,隨后體溫調節系統開始發揮作用,表現為皮膚濕潤度持續上升以促進蒸發散熱,因此熱負荷在受試者進入高溫環境3 min左右便開始下降;受試者回到中性溫度環境后,熱負荷出現“超越”現象,隨后熱負荷逐漸恢復,但直至實驗結束仍低于第1階段,這是由于人體在高溫環境中大量出汗,返回中性溫度環境后皮膚表面積蓄的汗液持續從皮膚表面帶走熱量;在過渡季和冬季工況下受試者進入低溫環境的初始時刻,由于空氣溫度和平均輻射溫度均低于皮膚溫度,所以全身熱負荷降低,且突變溫差越大熱負荷降低越多,隨后體溫調節系統開始發揮作用,表現為平均皮膚溫度持續降低以減少人體輻射散熱和對流散熱,因此熱負荷在受試者進入低溫環境2 min左右便開始逐漸上升,在回到中性溫度環境時,熱負荷逐漸恢復并趨于穩定。

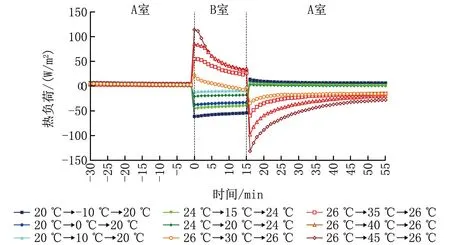
圖7 各工況下受試者全身熱負荷的逐時變化

3 討論

3.1 人體熱負荷與熱感覺的關系

由熱感覺和熱負荷逐時變化曲線可以看出,高溫到中性溫度突變瞬間,熱感覺出現明顯“冷感超越”現象的時刻對應于人體熱負荷發生“超越”的時刻。針對這種現象,圖8顯示了夏季工況下人體各項散熱量的逐時變化,散熱量為正值時說明人體向外界散熱,為負值時說明人體從外界得熱。可以看出:30 ℃環境中空氣溫度略低于皮膚溫度,人體通過對流換熱、輻射換熱和皮膚蒸發向外界散熱,但在空氣溫度更高的環境中由于空氣溫度近似于或高于皮膚溫度,導致人體通過對流換熱、輻射換熱向外界散熱很少(35 ℃)或從外界得熱(40 ℃和45 ℃),作為補償,皮膚蒸發散熱量隨著出汗量的增大而增大;從高溫環境到中性溫度環境后,人體皮膚蒸發散熱量急劇增大,總散熱量大于產熱量,導致人體出現冷感;在夏季4個工況中,45 ℃→26 ℃工況下皮膚蒸發散熱量增加幅度最大,也導致了該工況下“冷感超越”最明顯;隨著體溫調節系統開始發揮作用,皮膚蒸發散熱量逐漸下降,突變后的冷感逐漸消失;在突變后25 min左右皮膚蒸發散熱量基本趨于平穩,這與熱感覺的穩定時間較為一致。

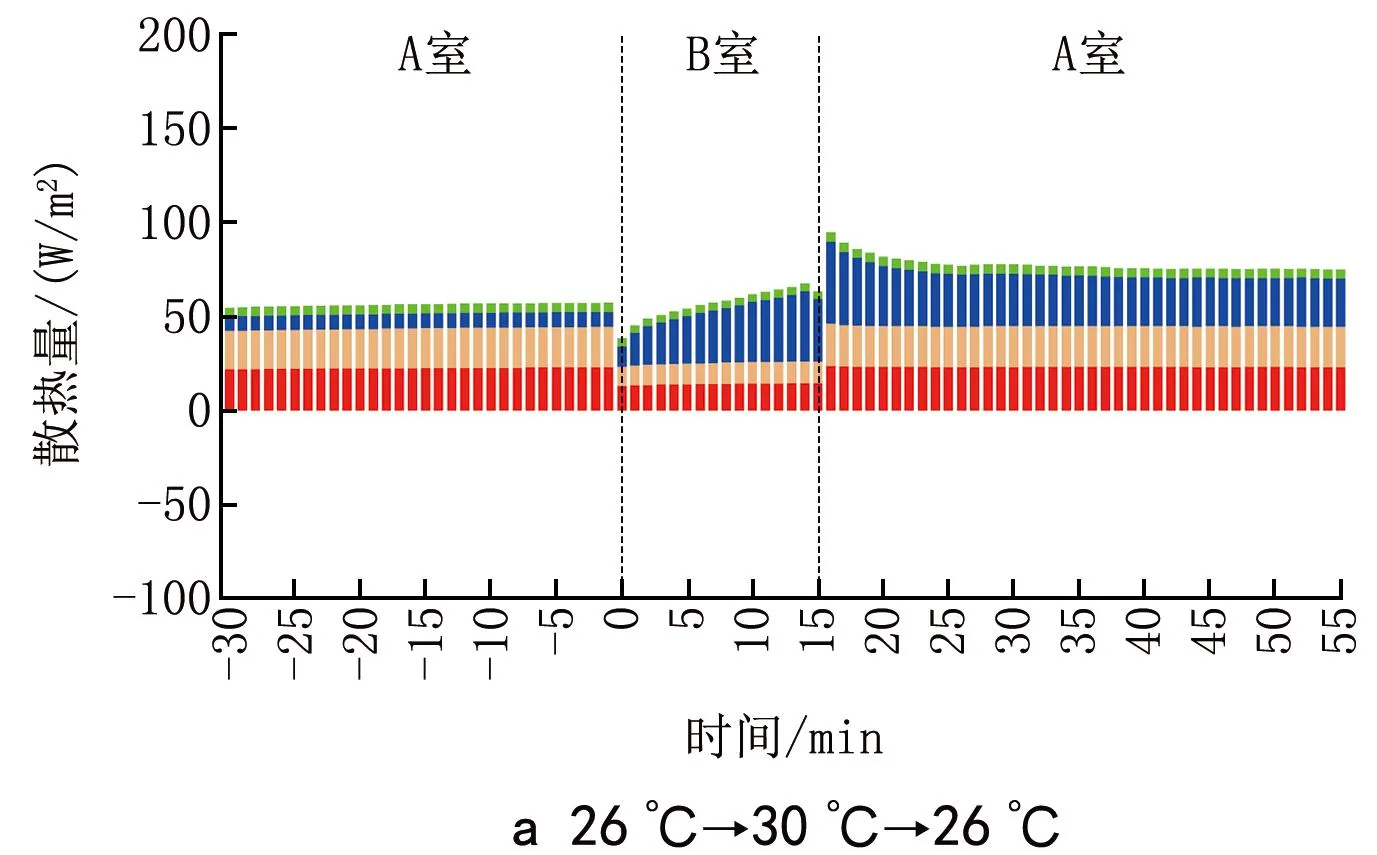
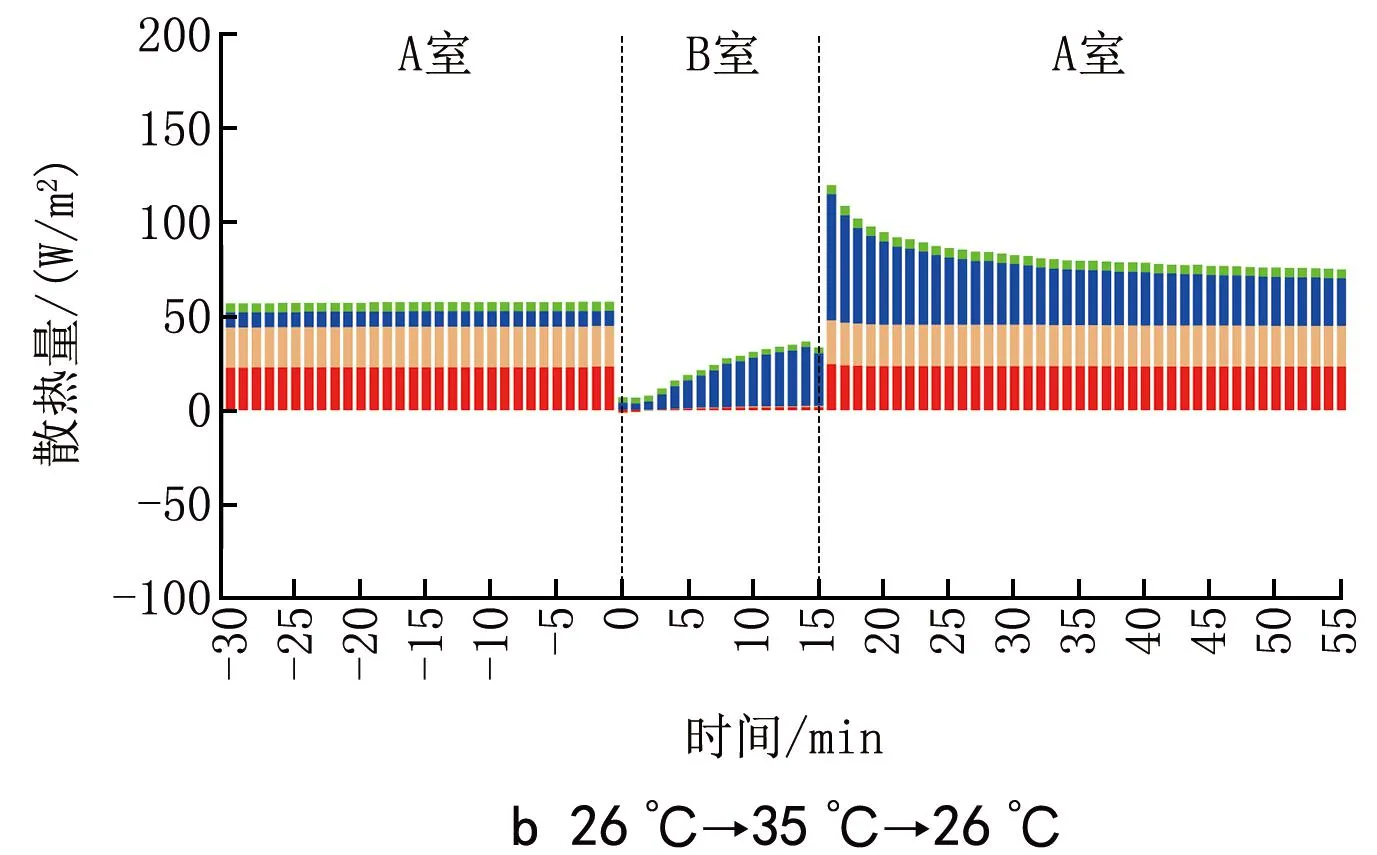
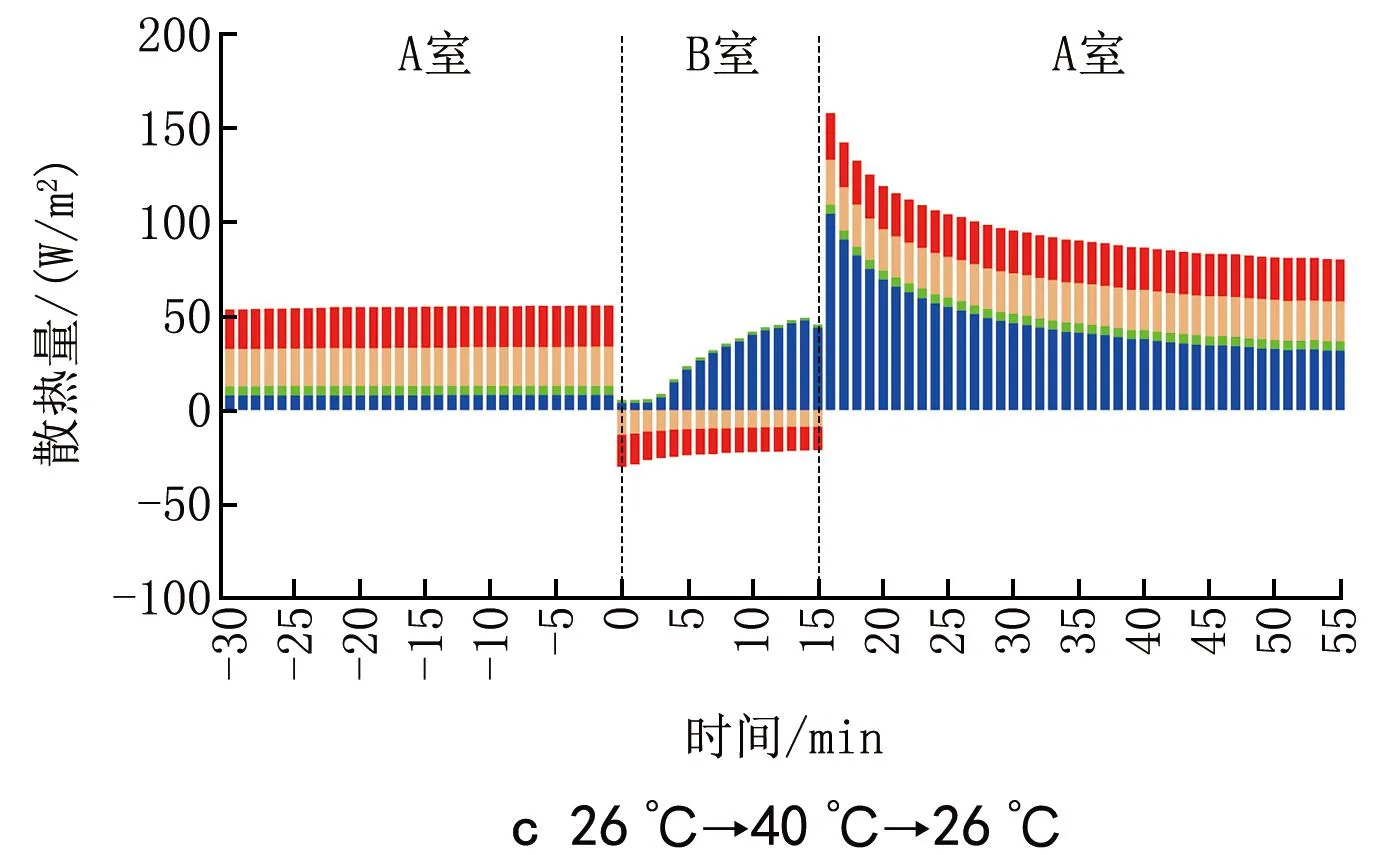
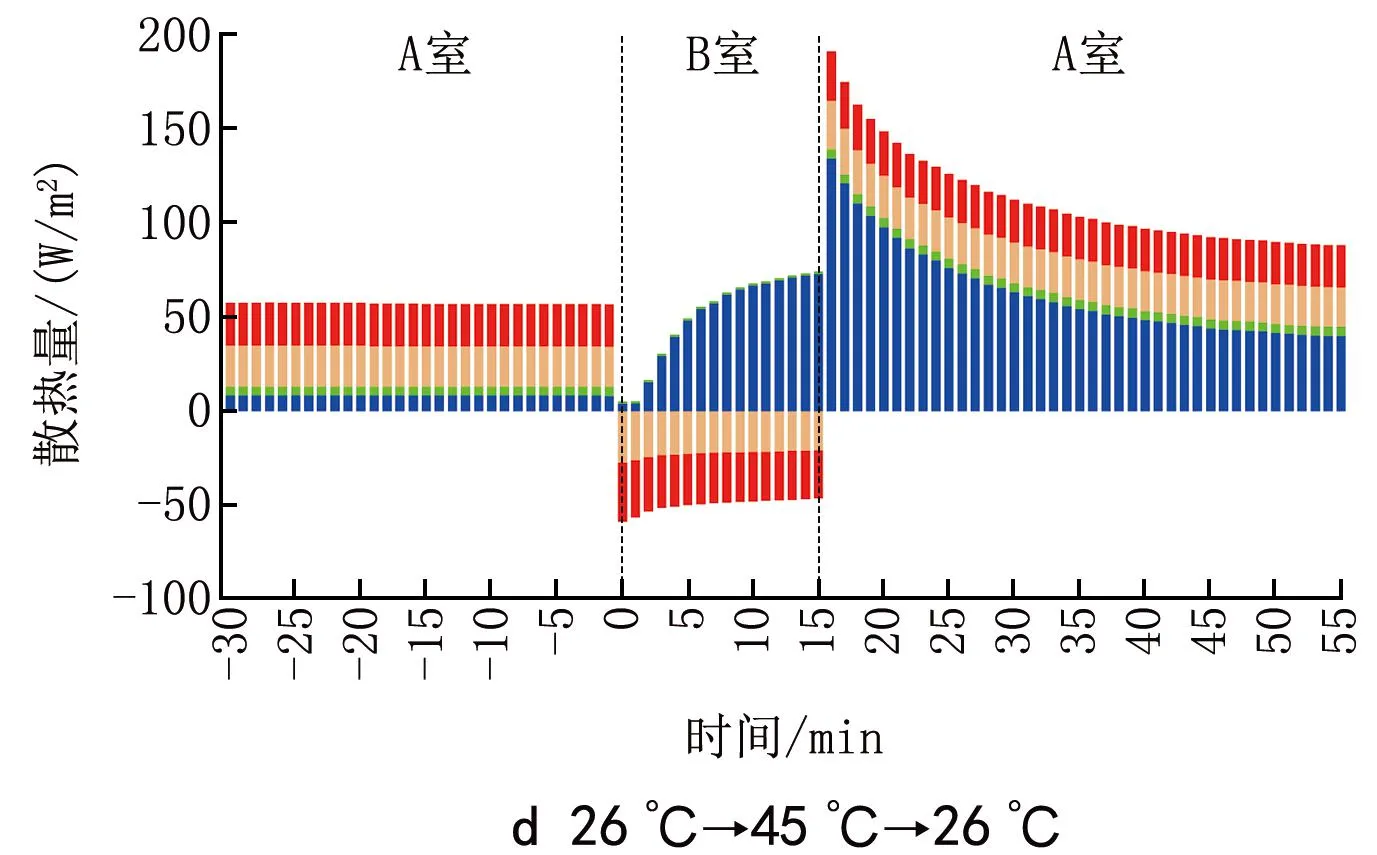
圖8 人體各項散熱量的逐時變化

3.2 基于皮膚溫度的熱感覺預測

溫度突變過程中,熱感覺與平均皮膚溫度及其變化率相關。因此動態熱環境中的人體熱感覺預測需要分別建立熱感覺模型的穩態項和動態項,動態熱感覺(TDTS)視為穩態項(Ts)與動態項(Td)之和,即

TDTS=Ts+Td

(9)

3.2.1預測模型穩態項Ts

將各工況3個階段最后1 min的熱反應視為穩態,之前的反應視為動態。對各個工況下全身熱感覺和平均皮膚溫度的穩態值作回歸分析,結果如圖9所示。全身熱感覺與平均皮膚溫度的回歸模型為

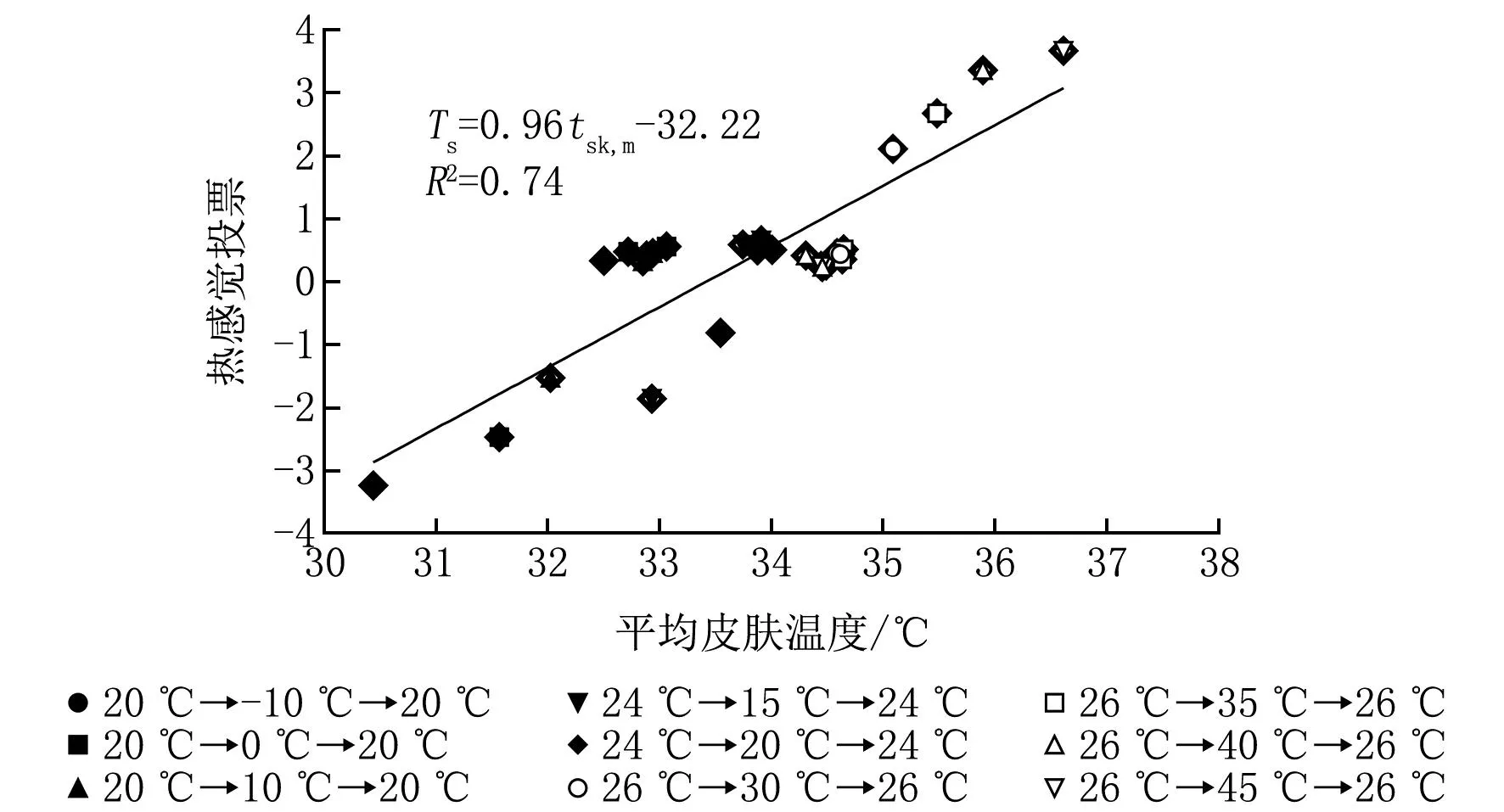
圖9 穩態情況下熱感覺與皮膚溫度的關系

Ts=0.96tsk,m-32.22 (R2=0.74)

(10)

由圖9可以看出,穩態情況下人體的全身熱感覺投票值與平均皮膚溫度呈較好的線性關系,平均皮膚溫度每升高1 ℃,全身熱感覺投票值增加0.96。對應熱感覺為中性的平均皮膚溫度即皮膚溫度的設定點為33.56 ℃,這與以往的研究結果[2]相差很小。

3.2.2預測模型動態項Td

動態項假定只與平均皮膚溫度變化率r有關,r可由下式計算:

(11)

式中tsk,mτ為τ時刻的平均皮膚溫度,℃;tsk,mτ-1為τ-1時刻的平均皮膚溫度,℃。

先按式(10)和逐時平均皮膚溫度計算熱感覺的穩態項,然后由動態熱感覺和式(9)計算得到熱感覺動態項,熱感覺動態項與平均皮膚溫度變化率的關系如圖10所示。

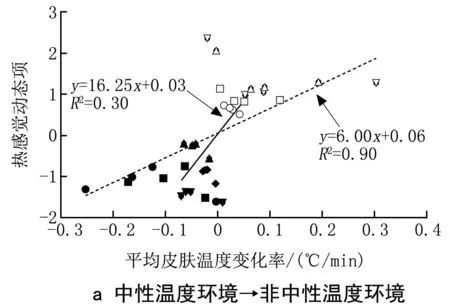
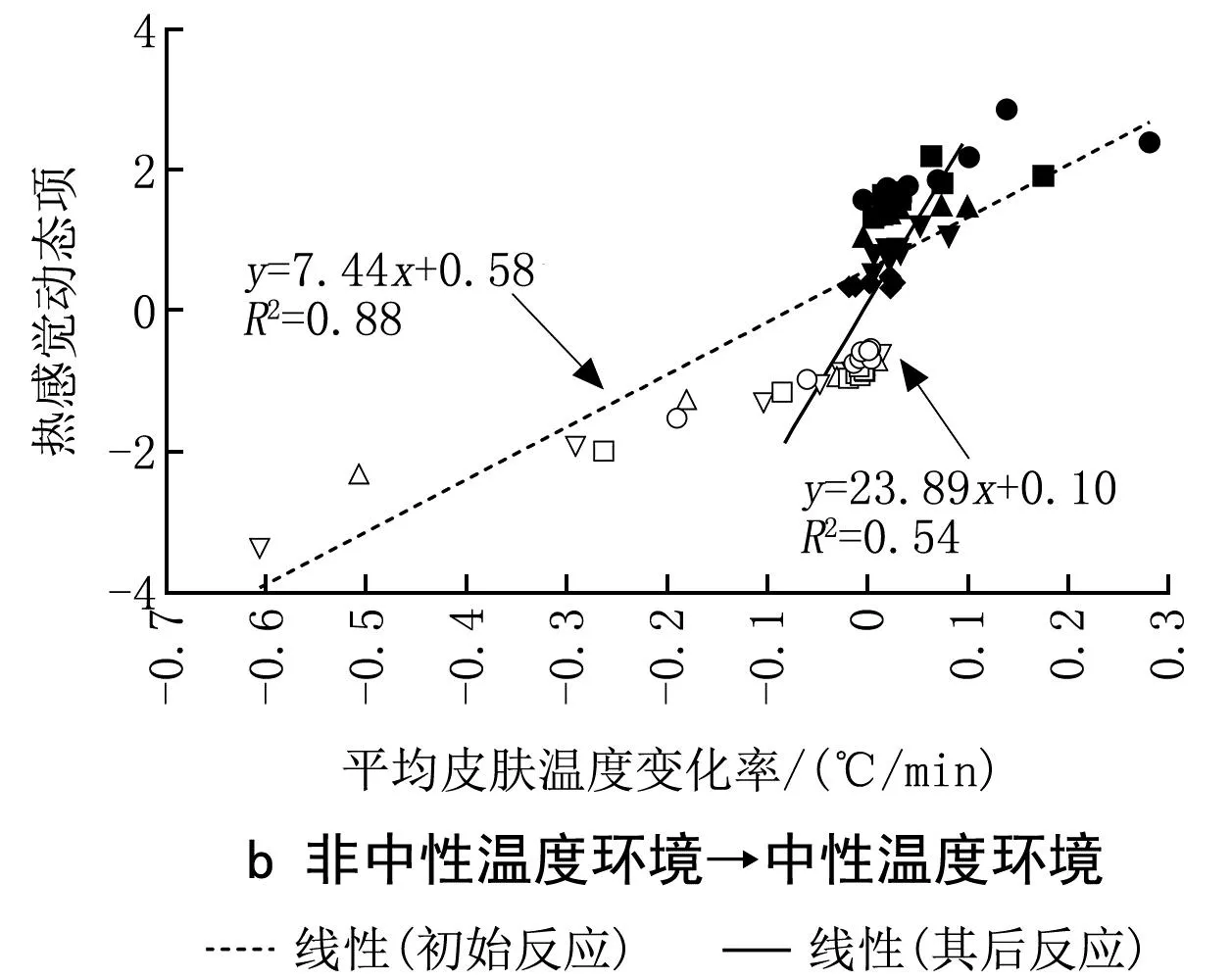
圖10 熱感覺動態項與平均皮膚溫度變化率的關系

由圖10可知,熱感覺動態項隨平均皮膚溫度變化率的變化而變化,突變初始時刻的平均皮膚溫度變化率較大,分散在兩邊,其后時刻的平均皮膚溫度變化率較小,集中在中間,故將平均皮膚溫度變化率r≤-0.1 ℃/min和r≥0.1 ℃/min的數據點看作初始反應,將-0.1～0.1 ℃/min間的數據點看作其后反應,分別作回歸。

中性溫度環境→非中性溫度環境:

初始反應

Td=6.00r+0.06 (R2=0.90)

(12)

其后反應

Td=16.25r+0.03 (R2=0.30)

(13)

非中性溫度環境→中性溫度環境:

初始反應

Td=7.44r+0.58 (R2=0.88)

(14)

其后反應

Td=23.89r+0.10 (R2=0.54)

(15)

可以看出:2種突變過程的初始反應中,受試者熱感覺動態項與平均皮膚溫度變化率呈顯著的線性關系,平均皮膚溫度變化率越大,熱感覺動態項越大,最大可達3.37;2種突變過程的其后反應中,受試者熱感覺動態項與平均皮膚溫度變化率的線性關系不再顯著,這是由于受試者的熱感覺和平均皮膚溫度在新環境中都達到穩定;熱感覺動態項隨平均皮膚溫度變化率線性變化的趨勢在初始時刻較為平緩,在其后時刻較為陡峭,即在其后時刻熱感覺隨皮膚溫度變化率的變化更為敏感。以上結果證實了Gagge等人提出的皮膚溫度變化率的重要作用[2],也可以更好地解釋不對稱現象。結合式(9)～(15)可得到基于皮膚溫度的人體熱感覺預測模型。

3.3 基于人體熱負荷的熱感覺預測

參考3.2節方法,將各工況3個階段最后1 min的熱反應視為穩態,之前的反應視為動態。選擇穩態反應的熱負荷LT和平均皮膚溫度tsk,m來確定熱感覺穩態項Ts。通過多元線性回歸獲得以下關系:

Ts=0.04LT+0.58tsk,m-19.06 (R2=0.92)

(16)

選擇動態反應的熱負荷變化量ΔLT和平均皮膚溫度變化率r來確定熱感覺動態項Td。通過多元線性回歸獲得以下關系式:

Td=0.03ΔLT+1.71r+0.08 (R2=0.87)

(17)

熱感覺穩態項Ts與熱感覺動態項Td之和即為基于人體熱負荷的熱感覺T′DTS預測模型:

T′DTS=Ts+Td

(18)

3.4 模型評估

圖11比較了熱感覺實測值與PMV模型、基于皮膚溫度的熱感覺預測模型、基于熱負荷的熱感覺預測模型預測值。可以看出,PMV模型對于溫度突變情況下人體熱感覺預測不準確,基于皮膚溫度和人體熱負荷的熱感覺預測模型預測效果較好。

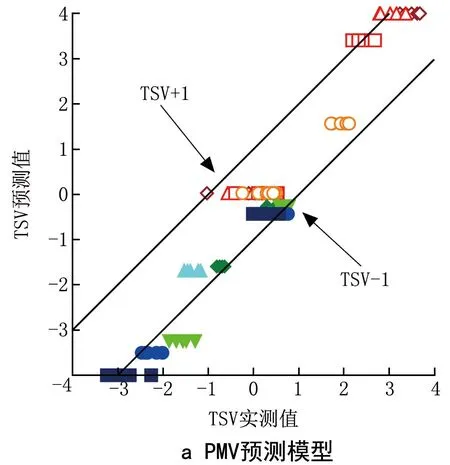
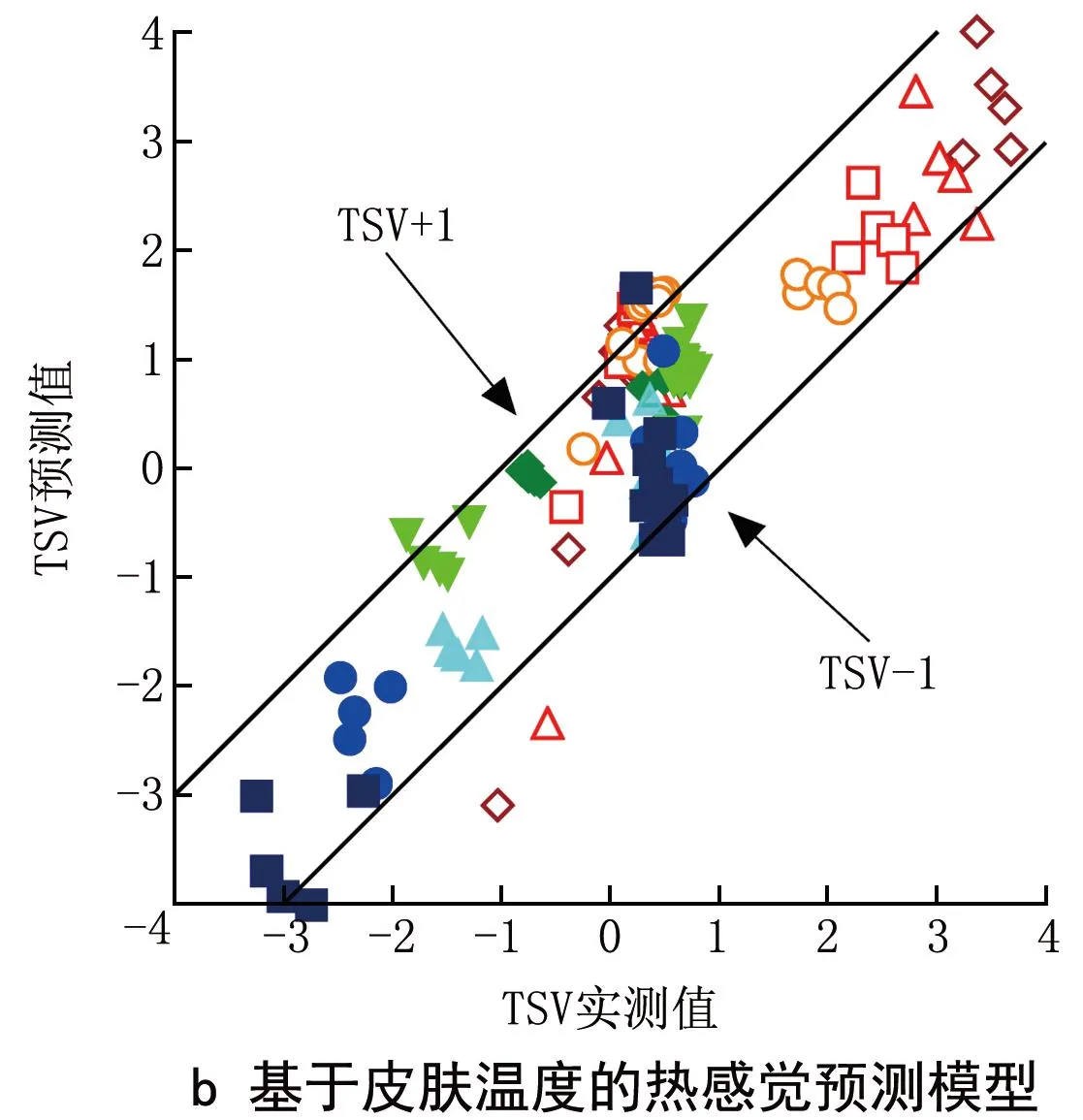
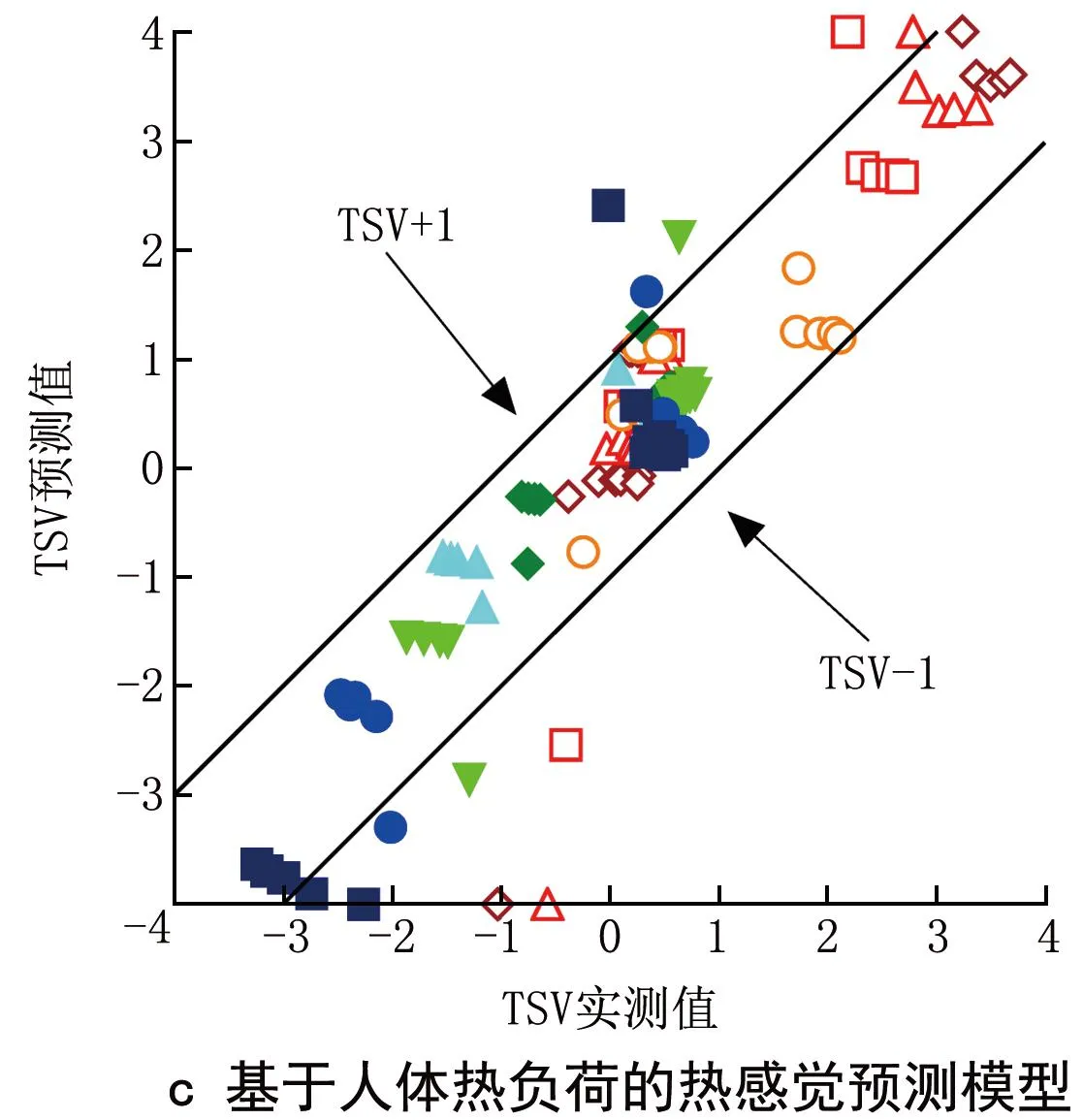
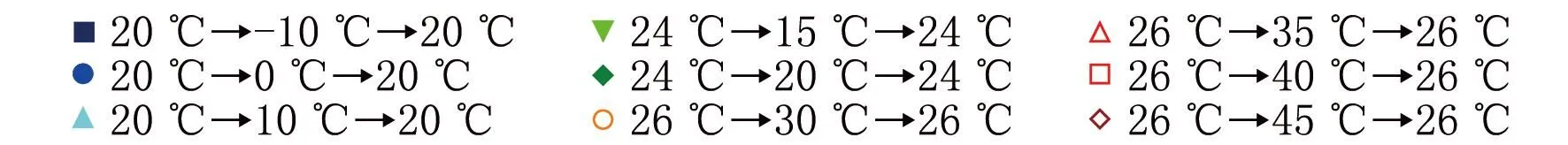
圖11 3種熱感覺預測模型的比較

表5顯示了各工況下熱感覺實測值與以上3種預測模型預測值之間的均方根誤差(RMSE)。

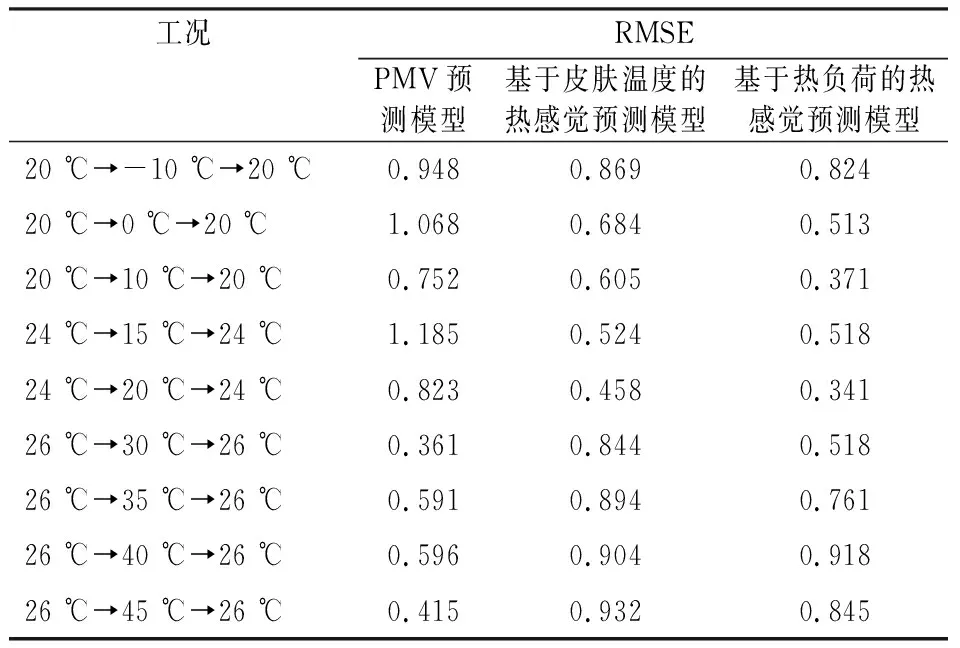
表5 模型驗證結果

可以看出:在冬季和過渡季工況下,PMV預測模型均方根誤差最大,甚至出現大于1的情況,其余2個模型均方根誤差較小,基于熱負荷的熱感覺預測模型效果最佳;在夏季工況下,PMV模型的均方根誤差最小,基于皮膚溫度的熱感覺預測模型的均方根誤差最大。

4 結論

1) 各工況突變過程中主觀反應變化均超前于生理反應,即出現心理超前現象;各工況突變前后2次中性溫度環境的熱感覺投票值不同,即出現熱感覺不對稱現象。

2) 在熱→中性突變工況中出現“冷感超越”現象,出現冷感的原因是人體從高溫環境進入中性溫度環境的瞬間,皮膚蒸發散熱量達到最大值,導致人體散熱量遠大于產熱量。隨著人體體溫調節系統開始起作用,人體的冷感逐漸消失。

3) 溫度突變動態環境中的熱感覺與平均皮膚溫度及其變化率均呈線性關系,進而得到了基于皮膚溫度的熱感覺預測模型。

4) 穩態階段的熱感覺與人體熱負荷和平均皮膚溫度呈線性關系,動態階段的熱感覺變化量與人體熱負荷變化量和平均皮膚溫度變化率呈線性關系,進而得到了基于熱負荷的熱感覺預測模型。

5) 對比了PMV模型、基于皮膚溫度的熱感覺預測模型、基于熱負荷的熱感覺預測模型在溫度突變情況下的預測性能,發現引入熱負荷的預測模型性能更好。