負壓廠房事故后壓力動態變化研究

薛 宇 趙 丹

(上海核工程研究設計院股份有限公司,上海)

0 引言

在工業生產活動中,可能會產生對人體有害的放射性物質,為防止放射性空氣及氣溶膠無控制地向室外逸散,必須通過排風維持室內的負壓環境[1]。事故工況下,大量帶放射性物質泄漏會造成室內壓力快速突增,破壞負壓平衡。因此,需要對事故工況進行分析研究,得到房間壓力的逐時變化數據,用于指導類似負壓廠房事故排風設計。

事故通風目前被大量應用于地下綜合管廊及制冷機房通風設計中[2-4],學者們通過模擬事故工況,得到了較優的氣流組織方案,可以減少事故危害。張倩茹等人對氨制冷機房發生泄漏時的排風口位置進行了優化設計,并指出房間門窗設置對氨氣排除有較大影響[5];王雪梅等人對管廊燃氣泄漏擴散進行了模擬,得到了不同泄漏孔徑下所需的事故通風換氣次數[6]。室內有害氣體泄漏研究主要集中于天然氣泄漏的模擬與實驗分析,并得到了對應的擴散模型[7-9]。陳琪對室內天然氣管道泄漏擴散特性進行了研究,得到了甲烷滯留區范圍,可用于指導事故現場檢測[10];于曉龍對不銹鋼波紋管內的天然氣泄漏進行了理論研究,得到了泄漏管段壓力與泄漏量的關系式[11]。目前研究多集中于易燃易爆物質泄漏后的檢測與通風排除,對于帶放射性物質泄漏過程中房間壓力變化的研究較少。

本文對負壓廠房內物質發生泄漏后房間壓力的變化進行理論與模擬研究,分析物質泄漏過程中房間的壓力變化及泄漏物質擴散情況,并計算房間恢復到初始狀態所需時間,為類似負壓廠房事故排風設計提供參考。

1 理論計算

1.1 負壓變化計算

負壓廠房日常工況下,室內開啟排風機(風量2 000 m3/h)維持-30 Pa的負壓,室外空氣由門縫滲透進入室內;事故工況下,內部帶放射性高溫水泄漏,室內短時間內達到正壓,室內帶放射性氣體由門縫排至室外。理論計算過程中進行了以下假設簡化:

1) 室內空氣為理想氣體;

2) 室外氣壓為標準大氣壓;

3) 室內初始溫度為26 ℃;

4) 破口泄漏流量恒定為28 kg/s,泄漏時長為24 s;

5) 破口高溫水泄漏的同時會產生氣體閃蒸,閃蒸率γ為40%;

6) 建筑物與環境沒有換熱;

7) 假設24 s后室內空氣溫度不再下降。

整個事故過程可以分為3個階段:0～24 s室內壓力不斷上升,24 s時室內達到最大正壓;受排風與門縫漏風影響,室內壓力與外界大氣壓達到平衡;排風機繼續運行,室內轉為負壓,門縫處空氣流向轉變,向室內補風,最終室內壓力恢復至-30 Pa。

使用理想氣體狀態方程與換熱公式進行室內壓力變化的動態計算,得到以下計算公式。

(1)

(2)

Q1=Qmγr+(100-26)Qmc1

(3)

(4)

tτ=t(τ-1)+Δt1(τ≤24 s)

(5)

tτ=t24(τ>24 s)

(6)

(7)

(8)

式(1)～(8)中n1為破口高溫水摩爾質量流速,mol/s;Qm為破口高溫水泄漏流量,kg/s;μ2為水蒸氣摩爾質量,kg/mol;n2為排風口空氣摩爾質量流速,mol/s;ρa為空氣密度,kg/m3;Qv1為室內排風機流量,kg/s;μ1為空氣摩爾質量,kg/mol;Q1為破口高溫水每秒對室內輸入的熱量,kW;r為水的汽化潛熱,kJ/kg,取2 257.2 kJ/kg;c1為水的比熱容,kJ/(kg·℃),取4.2 kJ/(kg·℃);Δt1為Q1單位時間內對室內溫度的提升,℃;V1為室內空間體積,m3;c2為空氣的比熱容,kJ/(kg·℃),取1.012 kJ/(kg·℃);t為室內溫度,℃;n′為門縫處空氣摩爾流量,mol/s;Q為門縫處空氣流量,m3/h;p為室內壓力,Pa;n為室內空氣物質的量,mol;下標τ為時間,s。

根據經驗公式,門縫處空氣流量Qτ為

(9)

式中 1.03為混凝土拼縫接縫等的附加泄漏量系數;A為門縫有效漏風面積,m2;Δp為室內外壓差,Pa;z為指數,一般取2;1.25為不嚴密處附加系數;N2為漏風疏散門數量。

采用式(1)～(9)進行700 s的逐時計算,得到室內壓力的動態變化,并繪制室內壓力隨時間的變化曲線及門縫處空氣流量隨時間的變化曲線,如圖1、2所示。

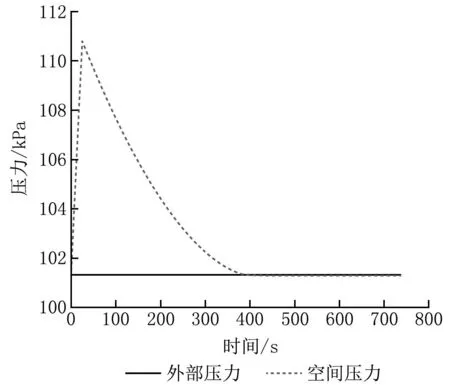
圖1 室內壓力隨時間的變化

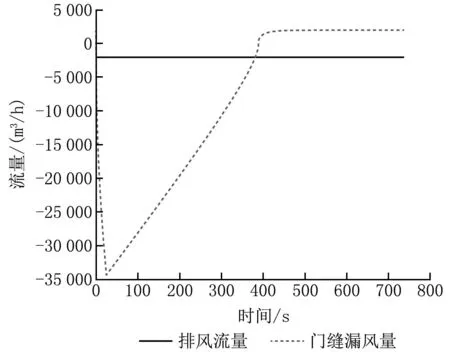
圖2 門縫處空氣流量隨時間的變化

計算可知,24 s時,室內達到最高壓力,為110.800 kPa,表壓為9.480 kPa,室內壓力增大9.505 kPa,此時門縫處空氣流量最高,為34 252 m3/h。390 s時,室內外壓差為0 Pa,448 s時,室內外壓差重新變為-30 Pa。

0～24 s時,由于室內壓力遠大于室外,門縫處空氣流向為由室內向室外擴散,且于24 s達到空氣流量峰值,為34 169 m3/h;24 s后室內壓力逐步降低,內外壓差縮小;390 s時,室內壓力與外部壓力相等,門縫處空氣流量為0 m3/h;390 s后,室內變為負壓狀態,門縫處空氣流向發生轉換,至448 s時,室內與室外壓差恢復最初狀態,為-30 Pa,門縫處空氣流量也達到穩定,為2 000 m3/h。

1.2 參數敏感性分析

研究排風量、泄漏水與空氣的換熱量、門縫面積對室內壓力動態變化的影響。

調整排風量參數分別為2 000、5 000、10 000 m3/h,對比各工況下室內壓力峰值及門縫處空氣流量變化情況,得到對應的恢復負壓所需時間,如圖3、4所示。

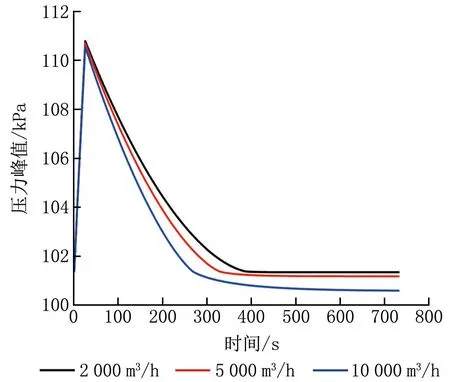
圖3 不同排風量下室內壓力峰值隨時間的變化

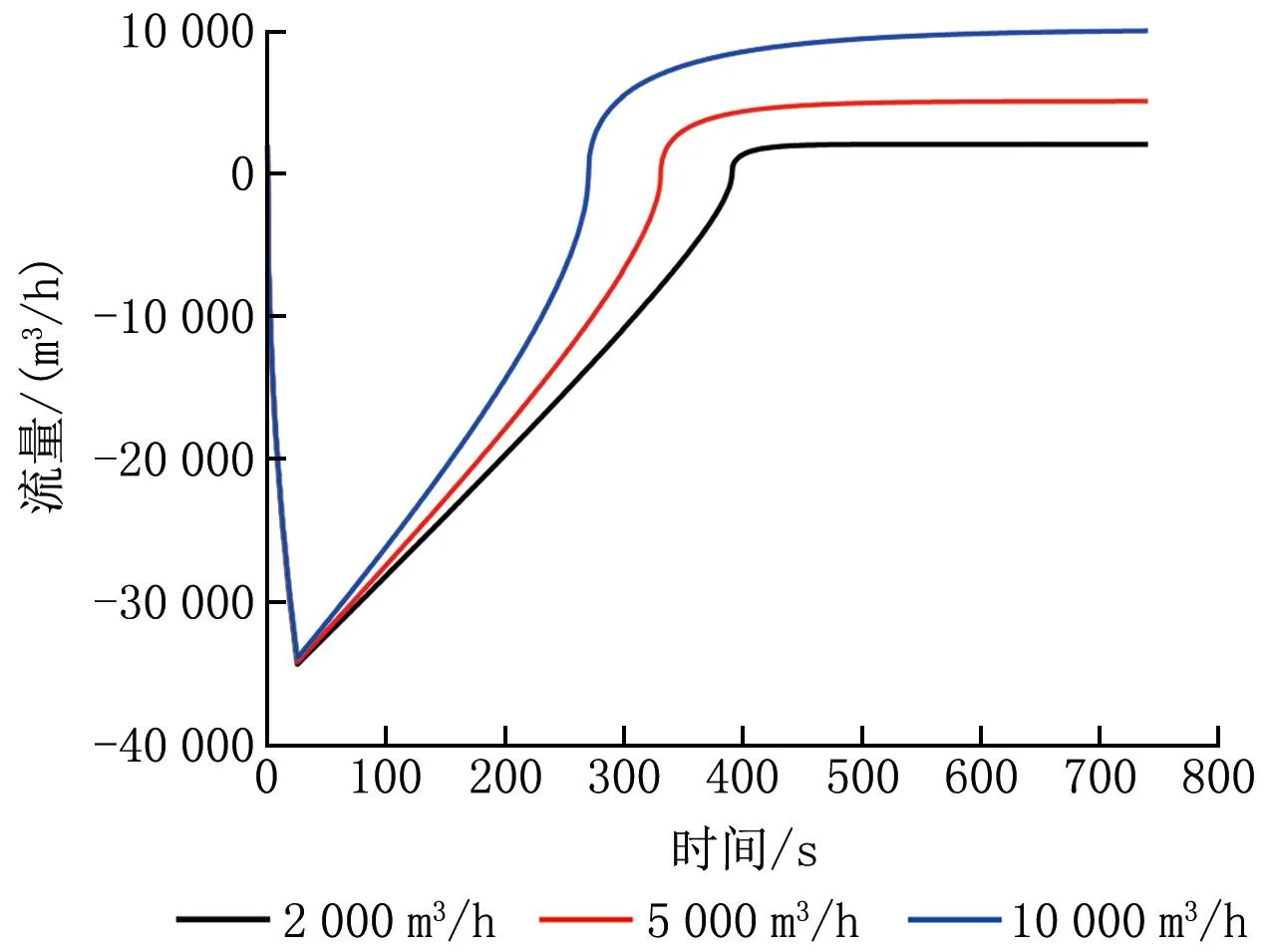
圖4 不同排風量下門縫處空氣流量隨時間的變化

由圖3、4可知,增大排風量可降低室內壓力峰值,并縮短室內恢復負壓所需時間。排風量為5 000 m3/h時,室內壓力峰值為110.436 kPa,室內外壓差為9.111 kPa,恢復負壓所需時間為337 s;排風量增大為10 000 m3/h時,室內壓力峰值為110.204 kPa,室內外壓差為8.879 kPa,恢復負壓所需時間為273 s。排風量增大150%,室內壓力峰值僅減小0.08%,恢復負壓所需時間縮短24.7%;排風量增大400%,室內壓力峰值僅減小0.21%,恢復負壓所需時間縮短39.0%。排風量增大對室內壓力影響較小。

調整泄漏水的溫度分別為30、50、75、100 ℃,對比各工況下室內壓力峰值及門縫處空氣流量變化情況,得到對應的恢復負壓所需時間,如圖5、6所示。

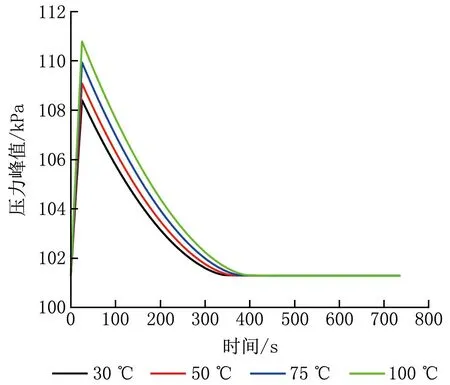
圖5 不同泄漏水溫度下室內壓力峰值隨時間的變化

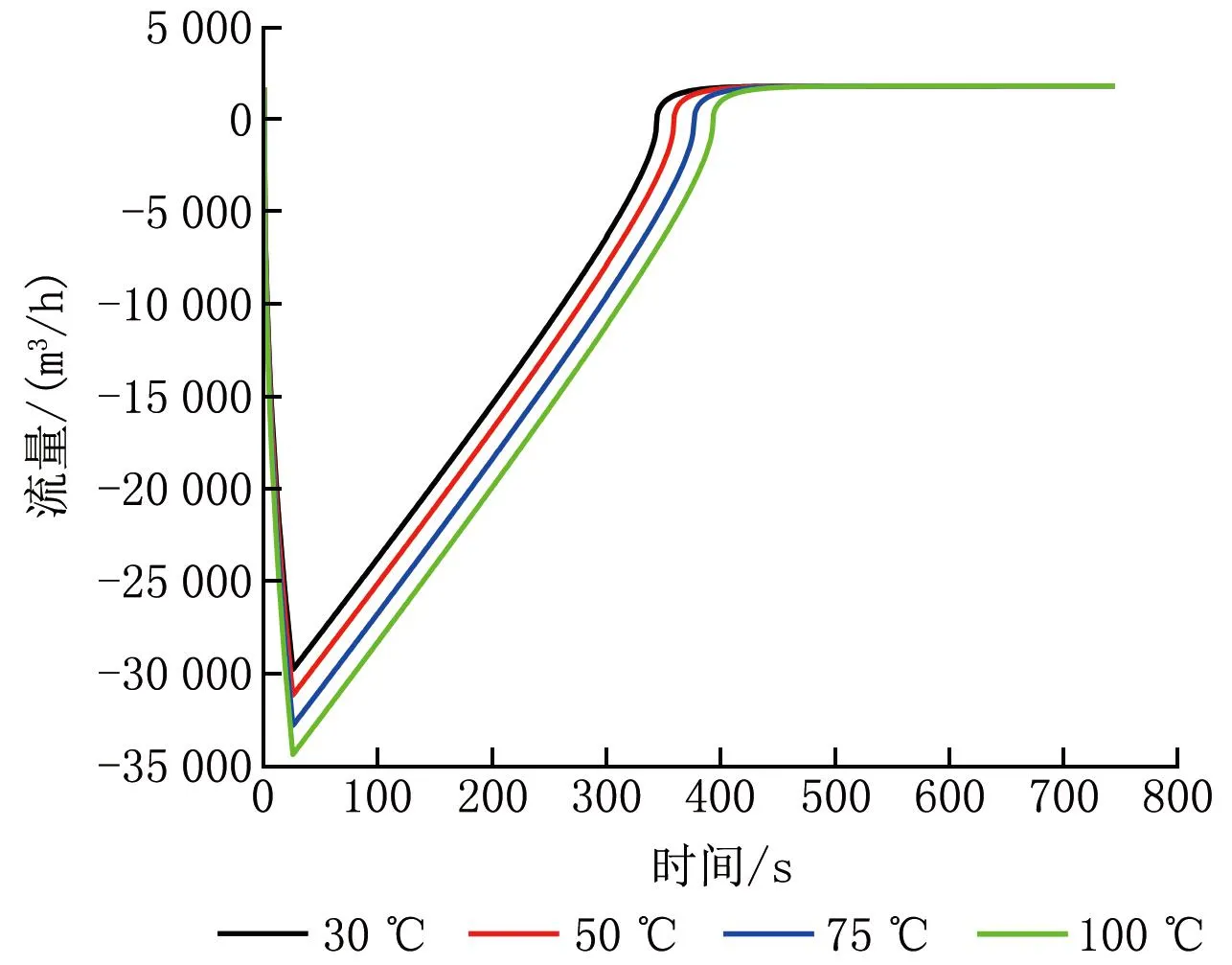
圖6 不同泄漏水溫度下門縫處空氣流量隨時間的變化

由圖5、6可知,泄漏水溫度對室內壓力峰值和恢復負壓所需時間的影響較大。泄漏水溫度為30 ℃時,室內壓力峰值為108.422 kPa,室內外壓差為7.097 kPa,恢復負壓所需時間為401 s;泄漏水溫度為50 ℃時,室內壓力峰值為109.100 kPa,室內外壓差為7.775 kPa,恢復負壓所需時間為416 s;泄漏水溫度為75 ℃時,室內壓力峰值為109.949 kPa,室內外壓差為8.624 kPa,恢復負壓所需時間為433 s。泄漏水溫度降低25%,室內壓力峰值減小0.77%,恢復負壓所需時間縮短3.3%;泄漏水溫度降低50%,室內壓力峰值減小1.50%,恢復負壓所需時間縮短7.1%。泄漏水與空氣的換熱量對室內壓力峰值影響較大,對恢復負壓所需時間影響較小。

調整門縫漏風面積分別為初始面積的2倍、5倍,對比各工況下室內壓力峰值及門縫處空氣流量變化情況,得到對應的恢復負壓所需時間,如圖7、8所示。

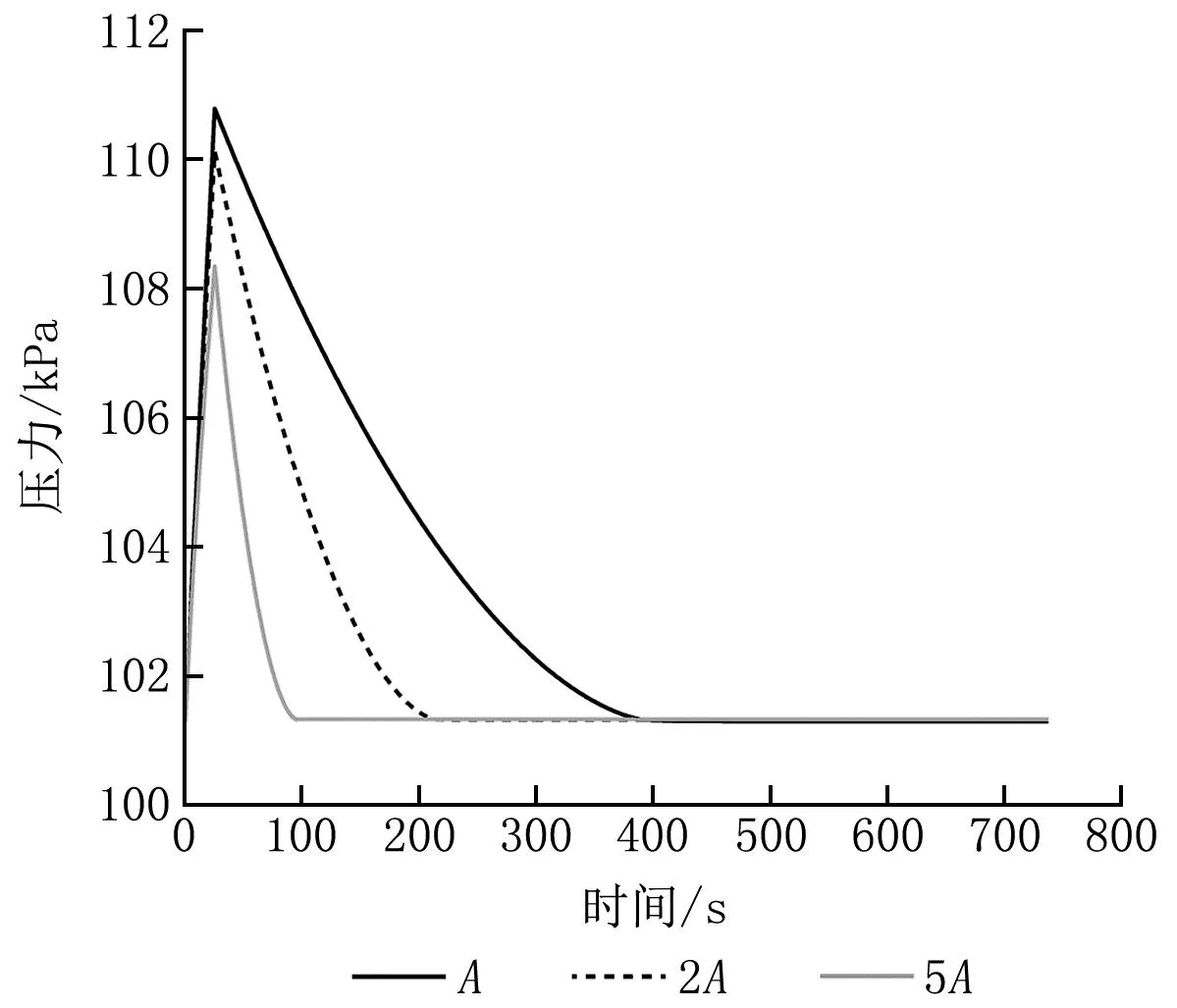
圖7 不同門縫漏風面積下室內壓力隨時間的變化

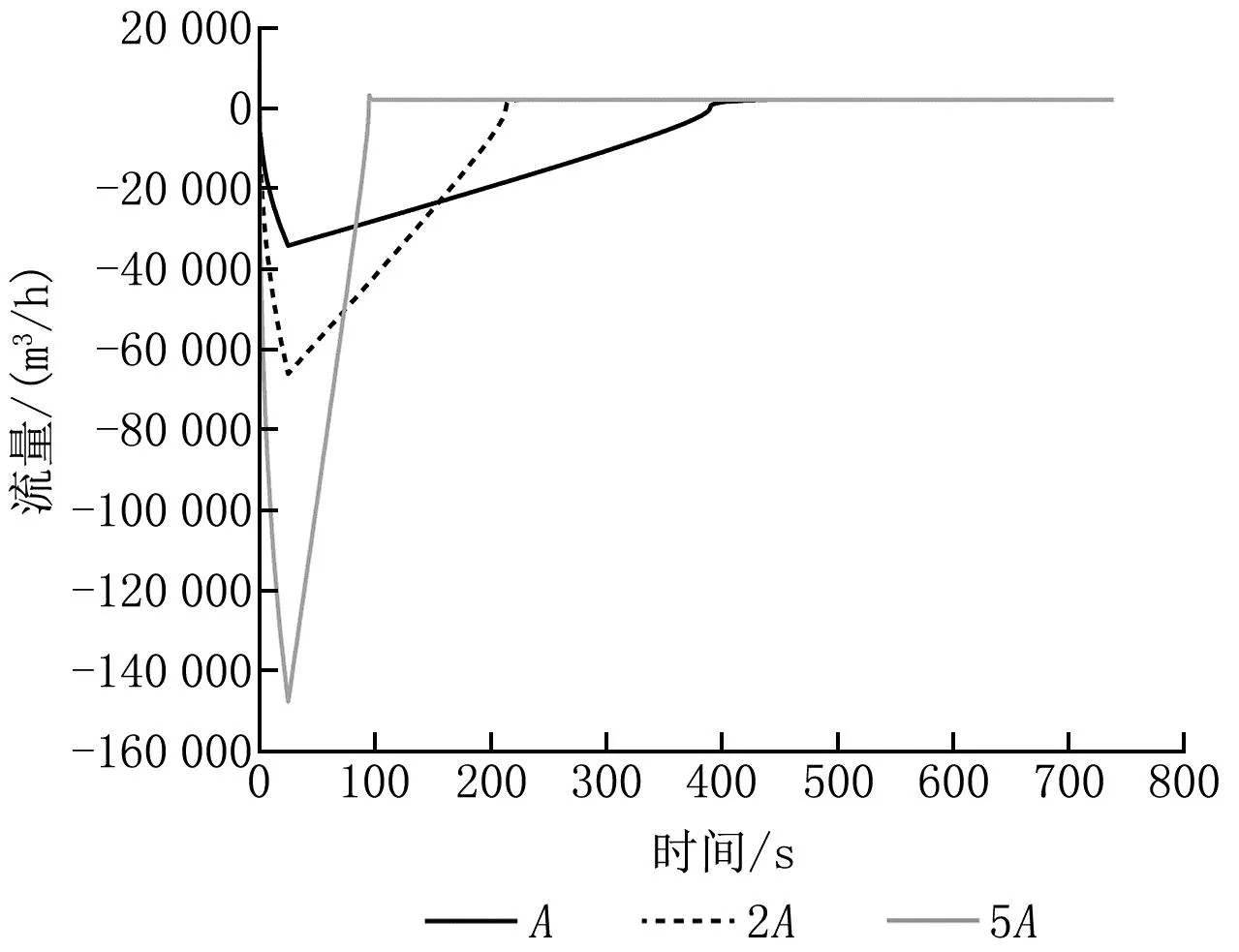
圖8 不同門縫漏風面積下門縫處空氣流量隨時間的變化

由圖7、8可知,門縫面積對室內壓力峰值和恢復負壓所需時間影響較大,門縫面積為初始面積的2倍時,室內壓力峰值為110.136 kPa,室內外壓差為8.489 kPa,恢復負壓所需時間為244 s,室內壓力峰值減小0.59%,恢復負壓所需時間縮短54%;門縫面積為初始面積的5倍時,室內壓力峰值為108.346 kPa,室內外壓差為7.021 kPa,恢復負壓所需時間為97 s,室內壓力峰值減小1.30%,恢復負壓所需時間縮短78%。門縫面積對室內恢復負壓所需時間影響較大,即室內有較多與外界連通的門時,恢度負壓所需時間會大幅縮短;門縫面積對室內壓力峰值影響較小。

2 數值模擬計算

2.1 幾何模型

建立負壓廠房簡化模型,如圖9所示。中部為高溫水蒸氣儲罐,事故工況下儲罐頂部出現直徑30 mm的泄漏點。排風口尺寸為500 mm×400 mm,位于儲罐單側,中心標高10 m。

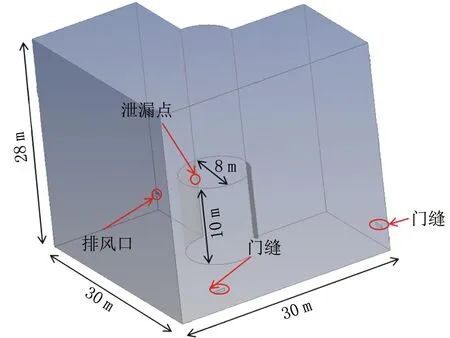
圖9 負壓廠房簡化模型

采用ANSYS Fluent軟件進行模擬計算,采用Meshing進行網格劃分,對送風口與門縫進行加密,并完成網格獨立性檢驗。采用非穩態計算,考慮重力,采用標準K-ε模型及組分運輸模型,設置混合物為不可壓縮理想氣體。邊界條件見表1。

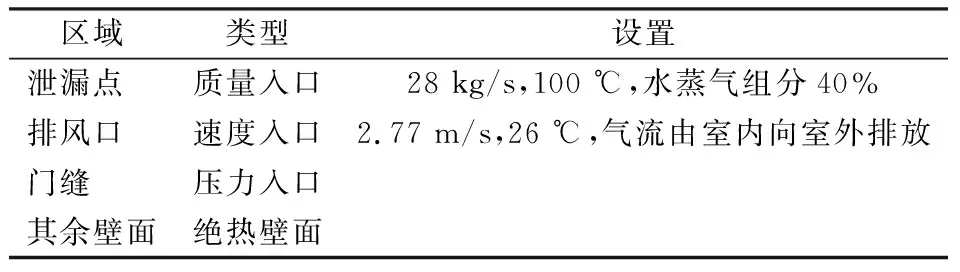
表1 邊界條件設置

2.2 0～24 s時段的模擬計算

24 s時的室內水蒸氣質量分數分布如圖10所示。粒子在24 s內會充斥整個房間,且可以到達門縫位置,向外溢出。24 s時,室內水蒸氣平均質量分數為2.7%。泄漏點附近水蒸氣質量分數較高,其余位置分布較均勻。

圖10 24 s時水蒸氣質量分數分布

選取特殊截面進行分析。平面1為2.5 m高度處的水平截面;平面2為排風口處的豎直截面。平面1的壓力分布云圖與水蒸氣質量分數分布如圖11、12所示。

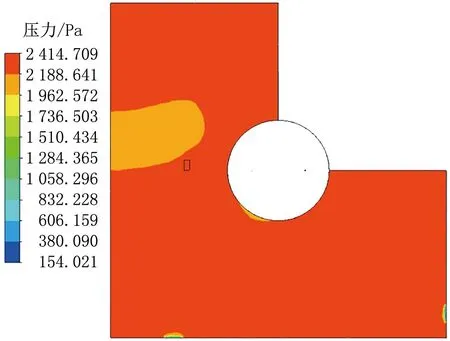
圖11 24 s時平面1的壓力分布云圖

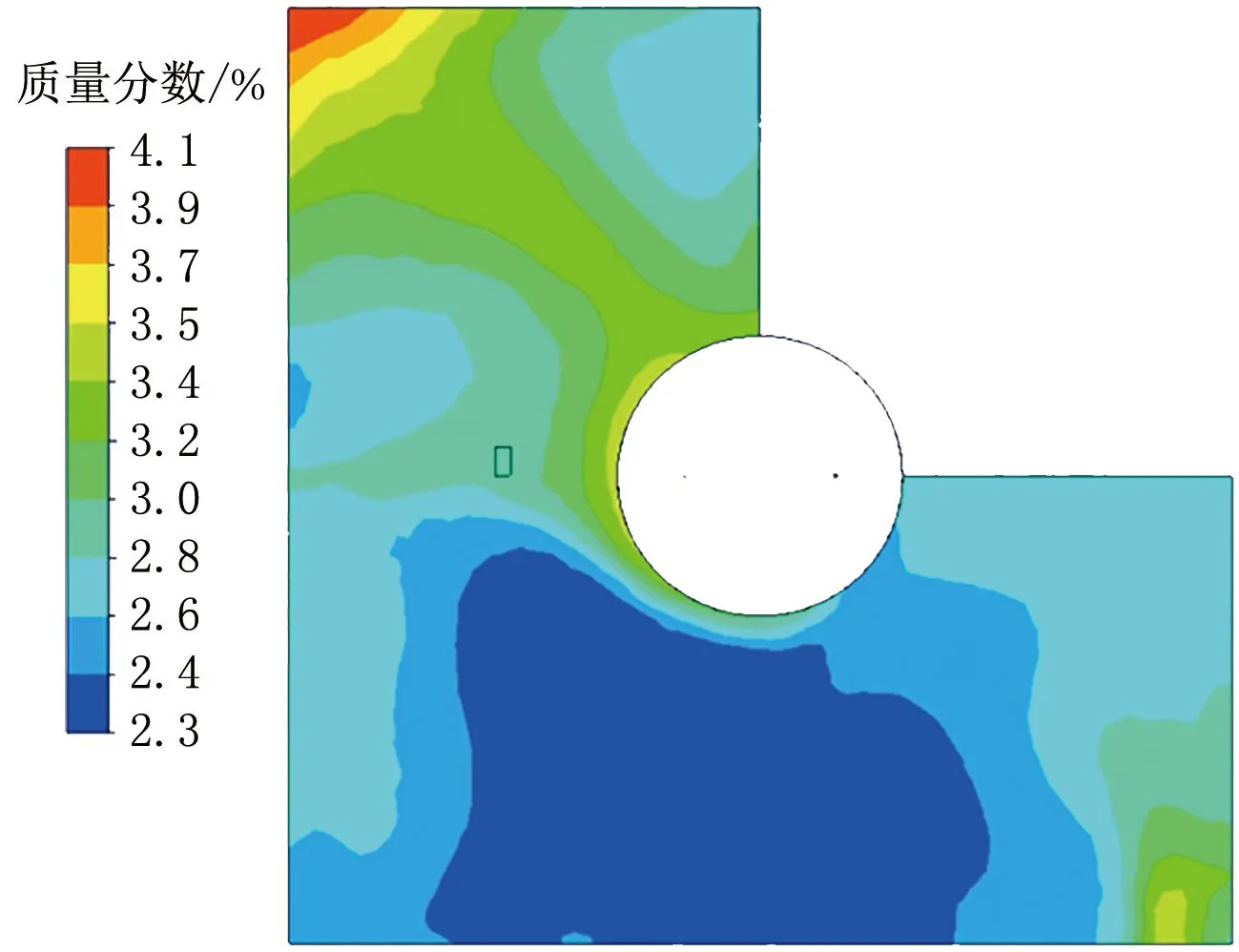
圖12 24 s時平面1的水蒸氣質量分數分布云圖

24 s時,平面1壓力分布大致均勻,基本維持在2 400 Pa左右,但門縫附近會存在壓力的梯度變化,這是由于門縫附近存在流體向外流出。內外壓差峰值為2 414 Pa。平面1水蒸氣質量分數基本維持在3.0%左右,房間角落位置存在循環死角,質量分數較大,門縫附近質量分數較小。

平面2壓力分布與水蒸氣質量分布如圖13、14所示。

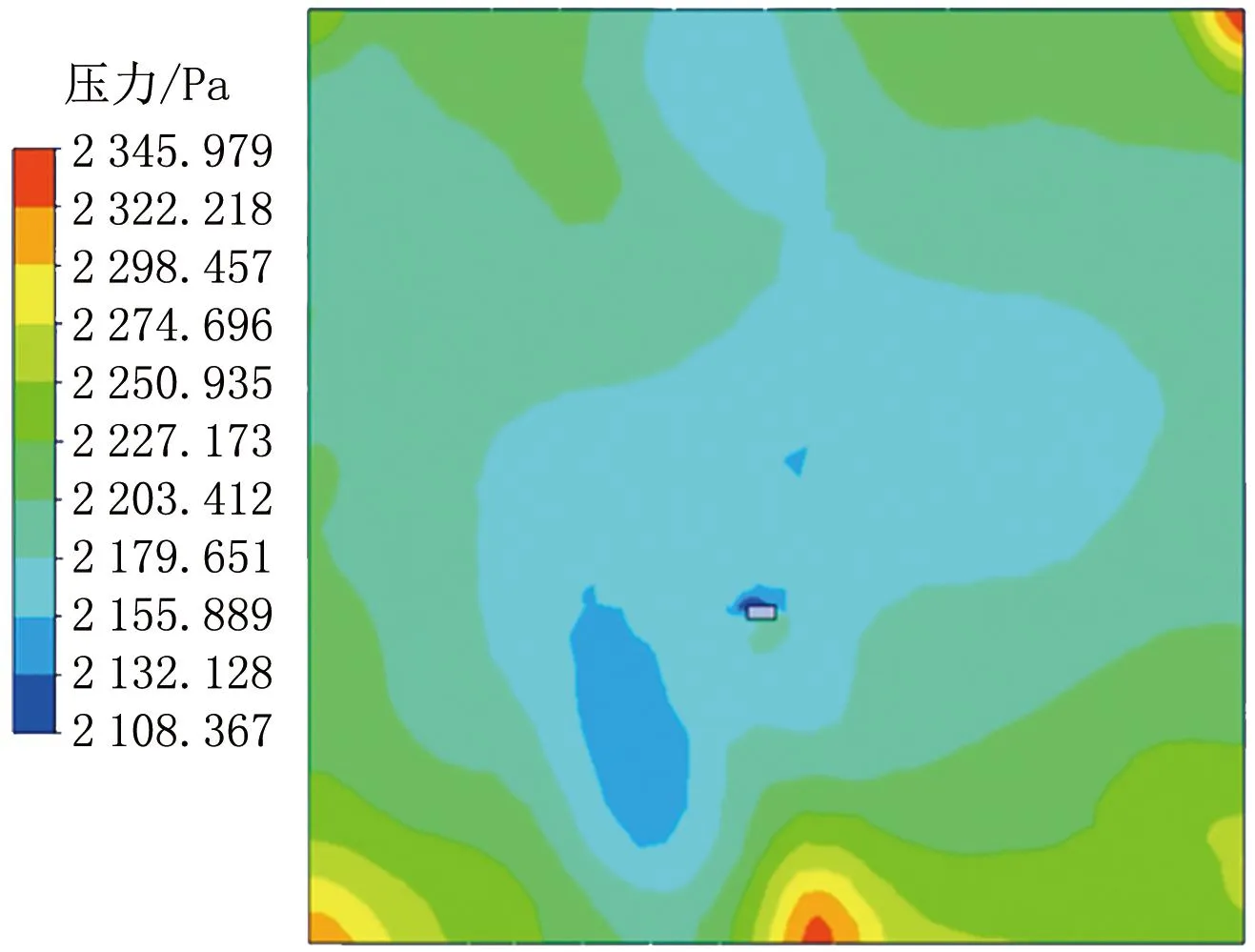
圖13 24 s時平面2的壓力分布云圖

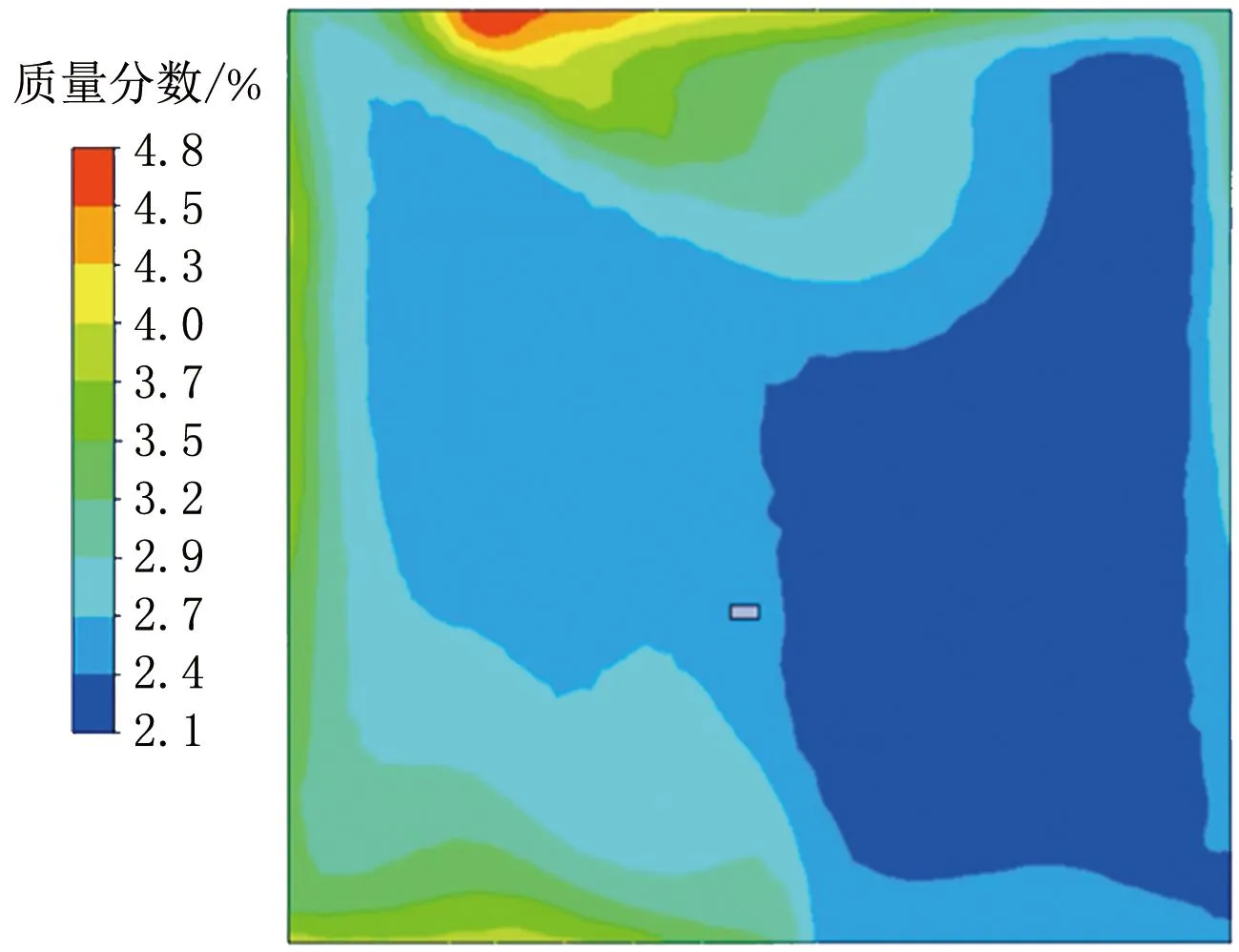
圖14 24 s時平面2的水蒸氣質量分數分布云圖

24 s時,平面2壓力分布基本均勻,均為高壓狀態,壓力基本維持在2 200 Pa左右,排風口附近壓力較低,角落處存在循環死角,壓力較高。門縫附近水蒸氣質量分數較小,這是由于水蒸氣持續向外排除導致的。

2.3 24～234 s時段的模擬計算

24 s之后,關閉泄漏點的入口,繼續模擬至234 s。234 s時的室內水蒸氣質量分數分布如圖15所示。234 s時室內水蒸氣質量分數平均為2.0%,較24 s時有所下降,且分布較均勻。

圖15 234 s時水蒸氣質量分數分布

234 s時平面1壓力分布與水蒸氣質量分數分布如圖16、17所示。

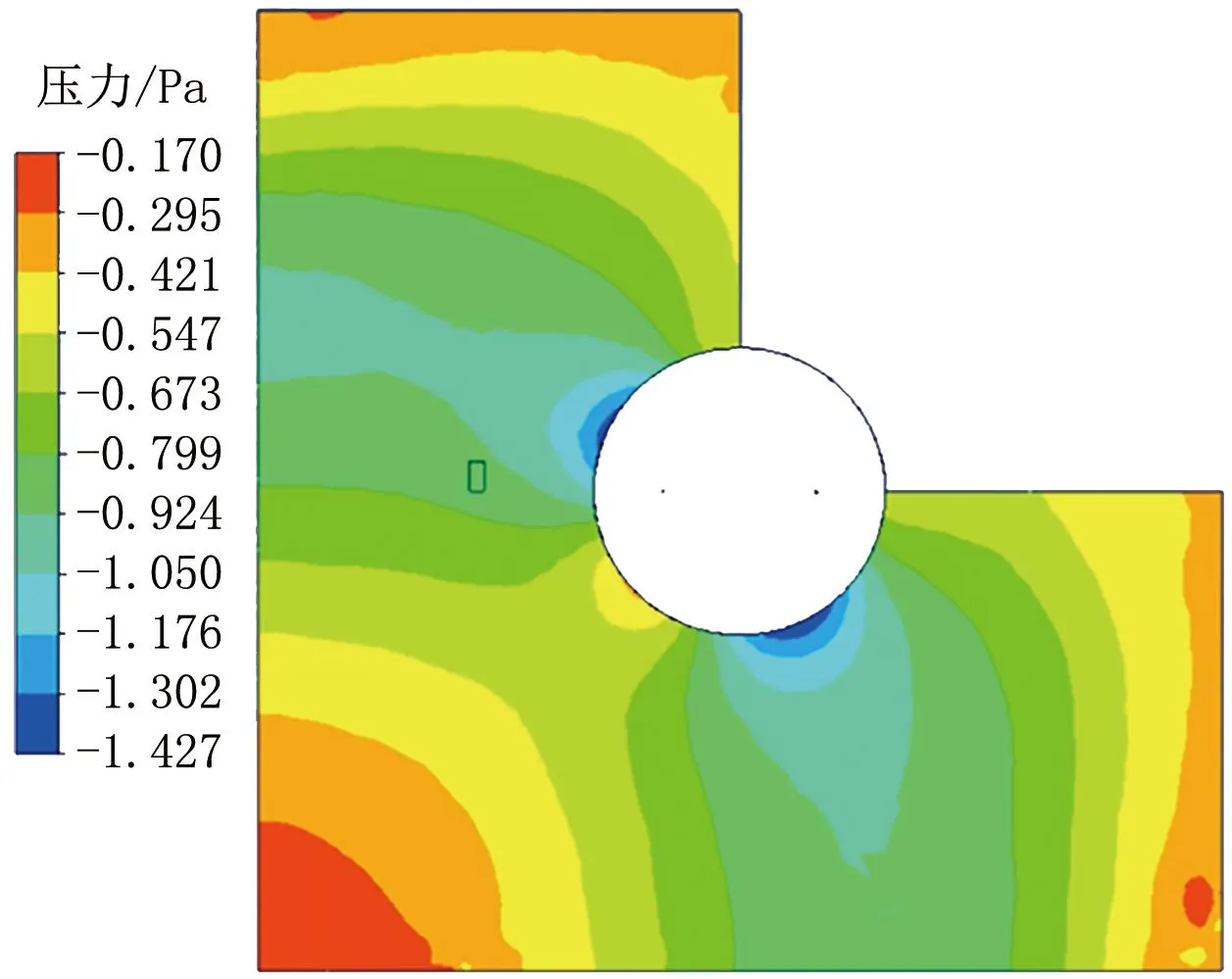
圖16 234 s時平面1的壓力分布云圖

234 s時,平面1均為負壓,壓力基本為-1 Pa左右,分布較均勻。房間角落處存在高壓區域,門縫處壓力也較高,流動方向為從門縫向室內流動。平面1水蒸氣質量分數基本維持在2.5%左右,門縫處由于有氣流進入,水蒸氣質量分數較小,存在濃度梯度。

平面2壓力分布與水蒸氣質量分數分布如圖18、19所示。

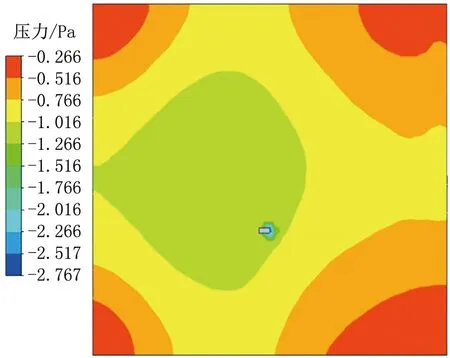
圖18 234 s時平面2的壓力分布云圖

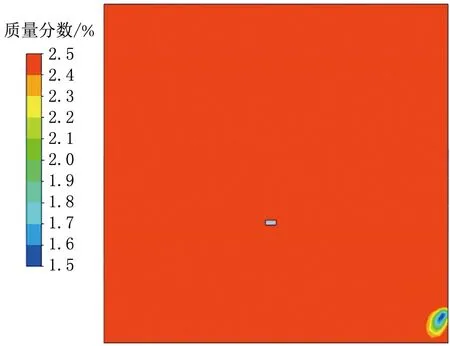
圖19 234 s時平面2的水蒸氣質量分數分布云圖

234 s時,平面2壓力均為負壓且分布均勻,基本維持在-0.7 Pa左右,排風口附近壓力較低,角落處存在循環死角,壓力較高。水蒸氣質量分數基本為2.5%左右,由于外部干凈氣流一直向室內輸送,門縫附近水蒸氣質量分數較小,為1.5%。

模擬計算的壓力峰值與理論計算值有誤差,但均在同一數量級,模擬氣體運動過程與理論分析相符,仍可表示事故發生工況下泄漏物質擴散情況與室內壓力分布。

3 結論

1) 得到了負壓廠房氣態物質泄漏后的理論計算方法。事故發生后,房間恢復負壓所需時間取決于3個因素:排風量、泄漏水與空氣的換熱量、門縫面積。

2) 根據理論計算,事故后24 s時,室內壓力達到峰值,為110.80 kPa,室內壓力增大9.505 kPa。室內外壓差恢復到0 Pa所需時間為390 s,恢復到-30 Pa所需時間為448 s。

3) 泄漏水與空氣的換熱量對室內壓力峰值影響較大,泄漏水溫度降低50%,室內壓力峰值減小1.5%,恢復負壓所需時間縮短7.1%;門縫面積對室內恢復負壓所需時間影響較大,門縫面積增大到5倍時,室內壓力峰值減小1.3%,恢復負壓所需時間縮短78%。

4) 根據模擬計算,事故后24 s時,室內壓力達到峰值,峰值為103.7 kPa,室內水蒸氣質量分數平均為2.7%,平均壓力為2.4 kPa;隨著水蒸氣由門縫向室外流動,234 s時,室內大部分區域水蒸氣質量分數為2.0%,內部均為負壓,基本為-1 Pa左右,室外空氣由門縫向室內流動,室內水蒸氣質量分數持續降低。室內存在氣流死角,后續可通過優化排風口位置減少氣流死角。

5) 事故發生后,由于大量水蒸氣輸入,室內壓力快速上升,在24 s時達到峰值。后續由于室內持續排風,室內壓力逐漸恢復至初始負壓狀態。模擬計算的壓力峰值與理論計算值有誤差,但均在同一數量級,模擬氣體運動過程與理論分析相符,可顯示事故發生工況下泄漏物質擴散情況與室內壓力分布。