基于分式二次規(guī)劃的互模糊函數(shù)賦形方法

楊 晨 吳 蕾 楊 威* 姜衛(wèi)東 劉永祥

①(國(guó)防科技大學(xué)電子科學(xué)學(xué)院 長(zhǎng)沙 410073)

②(北京跟蹤與通信技術(shù)研究所 北京 100094)

1 引言

在微弱目標(biāo)檢測(cè)問(wèn)題中，信號(hào)相關(guān)雜波是發(fā)射信號(hào)經(jīng)不同于目標(biāo)的延時(shí)和多普勒頻率的無(wú)關(guān)回波。由于其與目標(biāo)回波具有強(qiáng)相似性，極易對(duì)檢測(cè)造成影響。為了改善信號(hào)相關(guān)雜波下波形設(shè)計(jì)性能，文獻(xiàn)[1]在假設(shè)脈沖內(nèi)多普勒可以忽略不計(jì)的情況下，建立了相鄰距離單元雜波下的回波離散模型，并根據(jù)目標(biāo)和雜波在距離維的差異性，研究了基于最小化均方誤差(Mean Square Error,MSE)準(zhǔn)則的發(fā)射波形與接收濾波器聯(lián)合設(shè)計(jì)問(wèn)題。然而，在平臺(tái)與目標(biāo)之間存在快速運(yùn)動(dòng)的情況下，多普勒頻率通常不可忽略。因此上述問(wèn)題模型應(yīng)進(jìn)行修改以適應(yīng)多普勒頻率的展寬，同時(shí)問(wèn)題模型的維度也應(yīng)從距離維升高到二維模糊函數(shù)(Ambiguity Function,AF)[2]。

AF被定義為對(duì)具有不同時(shí)延和歸一化多普勒頻率的波形的匹配濾波器輸出響應(yīng)函數(shù)。AF是進(jìn)行波形設(shè)計(jì)與分析的有效工具，其可以有效揭示雷達(dá)系統(tǒng)的距離多普勒分辨率，同時(shí)還可以用來(lái)評(píng)估波形的抗干擾性能[3]。理想的雷達(dá)測(cè)量系統(tǒng)的AF要求在目標(biāo)所處距離-多普勒單元處具有單一峰值，但由于AF的等體積特性，實(shí)際波形通常難以滿足上述要求[4]。不少研究選擇通過(guò)AF賦形方法提高雷達(dá)系統(tǒng)的目標(biāo)檢測(cè)性能[5-22]。具體來(lái)說(shuō)，認(rèn)知雷達(dá)系統(tǒng)可以通過(guò)動(dòng)態(tài)環(huán)境數(shù)據(jù)庫(kù)和存儲(chǔ)在平臺(tái)中的環(huán)境信息來(lái)預(yù)測(cè)實(shí)際的散射環(huán)境[6]，從而使波形在先驗(yàn)干擾散射點(diǎn)所處距離-多普勒單元上的響應(yīng)盡可能小，在目標(biāo)所處距離-多普勒單元上的響應(yīng)盡可能高。

AF賦形方法中發(fā)射序列一般采用相位編碼序列。根據(jù)發(fā)射序列的相位編碼特性，通常模糊函數(shù)設(shè)計(jì)可以分為快時(shí)間維模糊函數(shù)設(shè)計(jì)和慢時(shí)間維模糊函數(shù)(Slow Time Ambiguity Function,STAF)設(shè)計(jì)。快時(shí)間發(fā)射波形是指包含一系列子脈沖的發(fā)射波形，文獻(xiàn)[5]提出了一種加速序列迭代優(yōu)化方法(Accelerated Iterative Sequential Optimization,AISO)實(shí)現(xiàn)局部模糊函數(shù)賦形，通過(guò)最小化特定距離-多普勒單元的加權(quán)積分旁瓣電平(Weighted Integrated Sidelobe Level,WISL)，提高雷達(dá)系統(tǒng)對(duì)指定區(qū)域的目標(biāo)探測(cè)能力。其結(jié)果與文獻(xiàn)[7,8]的梯度算法相比，具有更低的旁瓣與更快的收斂速度。文獻(xiàn)[9]研究了具有理想AF形狀的恒模快時(shí)間維發(fā)射波形與接收濾波器聯(lián)合設(shè)計(jì)問(wèn)題，在有限的信噪比損失約束條件下，通過(guò)交替迭代以及MM (Majorization-Minimization)算法實(shí)現(xiàn)了WISL和互補(bǔ)積分旁瓣電平(Complementary Integrated Sidelobe Level,CISL)的最小化，并在硬件系統(tǒng)上對(duì)所設(shè)計(jì)波形性能進(jìn)行驗(yàn)證。

慢時(shí)間發(fā)射波形是指由恒定脈沖重復(fù)間隔(Pulse Repetition Interval,PRI)的一系列脈沖組成的信號(hào)，其對(duì)應(yīng)的距離-多普勒響應(yīng)可以理解為STAF。文獻(xiàn)[10]首先提出了STAF賦形的概念，其主要思想為最小化發(fā)射波形AF在某些特定單元的平均值，并且通過(guò)最大塊改進(jìn)方法(Maximum Block Improvement,MBI)以及共軛超對(duì)稱四階張量理論，解決了問(wèn)題模型帶來(lái)的四階多項(xiàng)式優(yōu)化難題。針對(duì)上述模型帶來(lái)的復(fù)雜多項(xiàng)式，文獻(xiàn)[11]還提出了一種四次黎曼信賴域算法，其首先將問(wèn)題模型轉(zhuǎn)化為復(fù)圓黎曼流形上的無(wú)約束優(yōu)化問(wèn)題，然后設(shè)計(jì)一種新的黎曼信賴域優(yōu)化算法以求得迭代解。文獻(xiàn)[12]在峰值平均功率比(Peak-to-Average power Ratio,PAR)約束下，以最大化信干噪比(Signal-to-Interferenceplus-Noise Ratio,SINR)為準(zhǔn)則，同樣構(gòu)造了一個(gè)復(fù)雜四次函數(shù)優(yōu)化問(wèn)題。同時(shí)，提出一種將MM與坐標(biāo)下降(Coordinate Descent,CD)相結(jié)合的方法，解決了恒模(Constant Modulus,CM)約束下的慢時(shí)間維AF設(shè)計(jì)問(wèn)題。

為了充分利用雷達(dá)聯(lián)合收發(fā)處理的自由度，基于非匹配濾波體制，文獻(xiàn)[13]引入發(fā)射波形與接收濾波器失配的互模糊函數(shù)(Cross-Ambiguity Function,CAF)設(shè)計(jì)概念，設(shè)計(jì)的序列可以用作發(fā)射波形與接收濾波器，也可用于MIMO雷達(dá)。文獻(xiàn)[14]針對(duì)低旁瓣CAF設(shè)計(jì)所帶來(lái)的高階多項(xiàng)式優(yōu)化(High-Order Polynomial,HOP)問(wèn)題，提出了一種廣義MBI方法，通過(guò)為原線性張量函數(shù)設(shè)計(jì)等效多項(xiàng)式函數(shù)，降低了計(jì)算復(fù)雜度。文獻(xiàn)[15]研究了離散與連續(xù)CAF賦形問(wèn)題，通過(guò)設(shè)計(jì)一對(duì)發(fā)射波形與接收濾波器，最小化與既定CAF之間的累計(jì)平方誤差。與此同時(shí)，該方法還對(duì)模板所關(guān)注的區(qū)域加大了權(quán)重，然而權(quán)重項(xiàng)的加入導(dǎo)致優(yōu)化問(wèn)題難度增大，因此文獻(xiàn)[15]忽略了發(fā)射波形的PAR約束。

在CAF賦形問(wèn)題中，倘若以最大化SINR為優(yōu)化準(zhǔn)則，目標(biāo)函數(shù)經(jīng)化簡(jiǎn)通常為二次分式形式。前期文獻(xiàn)[15,18]中的常規(guī)解決方法是利用丁克爾巴赫算法將其化為多項(xiàng)式形式，再利用MM算法等優(yōu)化方法求解。基于此研究背景，為了增強(qiáng)波形對(duì)微弱運(yùn)動(dòng)目標(biāo)的檢測(cè)能力，同時(shí)提高其運(yùn)算效率，本文研究了一種發(fā)射波形與接收濾波器CAF賦形策略，并提出了一種高效迭代求解方法。其基本思路是在信號(hào)相關(guān)雜波背景下，選取最大化接收端SINR為優(yōu)化準(zhǔn)則，同時(shí)為了保證最大化雷達(dá)發(fā)射機(jī)功率效率，在優(yōu)化模型中引入CM約束，通過(guò)對(duì)發(fā)射與接收濾波器的交替迭代優(yōu)化求得最優(yōu)解。對(duì)于模型所帶來(lái)的NP (Non-deterministic Polynomial)難分式二次規(guī)劃(Fractional Quadratic Programming,FQP)問(wèn)題，本文將其轉(zhuǎn)化為單模二次規(guī)劃(Unimodular Quadratic Programming,UQP)問(wèn)題，并通過(guò)類冪迭代(Power Method-Like,PML)方法進(jìn)行求解。此外，為了使波形具有更高的自由度和更好的實(shí)用性，在該模型下進(jìn)一步考慮了低PAR約束下的優(yōu)化問(wèn)題，并且通過(guò)最近鄰向量法求解最優(yōu)的發(fā)射波形與接收濾波器。最后，實(shí)驗(yàn)仿真與實(shí)測(cè)數(shù)據(jù)表明，相對(duì)于經(jīng)典CAF賦形方法，本文設(shè)計(jì)的發(fā)射波形與接收濾波器能實(shí)現(xiàn)更高的SINR值，同時(shí)具有較低的運(yùn)算復(fù)雜度。

2 問(wèn)題模型

x=[x(1),x(2),...,x(N)]T∈CN×1為單基地雷達(dá)系統(tǒng)在一個(gè)脈沖重復(fù)間隔內(nèi)發(fā)射的碼長(zhǎng)為N的波形，(·)T代表矩陣的轉(zhuǎn)置，則接收端的N維觀測(cè)向量r=[r(1),r(2),...,r(N)]T∈CN×1，R 和 C分別代表實(shí)數(shù)域和復(fù)數(shù)域，可以表示為[15]

其中，NS是干擾點(diǎn)數(shù)量，ρm代表第m個(gè)干擾散射點(diǎn)的回波復(fù)幅度，是第m個(gè)干擾散射點(diǎn)的歸一化多普勒頻率。歸一化即為將多普勒頻率區(qū)間均勻分為Nv份，設(shè)置目標(biāo)的多普勒頻率vtarget=0，并將干擾的多普勒頻率歸一化到目標(biāo)上。rm是第m個(gè)干擾散射點(diǎn)所處距離單元，Jr∈CN×N是移位矩陣，其第 (a,b)個(gè)元素定義為[11]

為了提升回波經(jīng)信號(hào)處理后的信干噪比，針對(duì)接收回波信號(hào)設(shè)計(jì)非匹配濾波器h=[h(1),h(2),...,h(N)]T∈CN×1，(·)H代表矩陣的共軛轉(zhuǎn)置，非匹配濾波輸出信號(hào)可以表示為

其中，P(vtarget)=diag(p(vtarget))，diag(·)表示對(duì)向量構(gòu)造對(duì)角矩陣。

由于干擾d(x)與噪聲n不相關(guān)，式(4)中干擾噪聲部分能量可以近似用C(x,h)∈R表示為

假設(shè)目標(biāo)的回波能量可以表示為G(x,h)∈R

當(dāng)發(fā)射端信號(hào)x滿足恒模約束時(shí)，接收端信干噪比可以表示為

在發(fā)射波形滿足恒模約束的條件下，通過(guò)設(shè)計(jì)發(fā)射信號(hào)與接收濾波器的互模糊賦形方法，最大化信干噪比的問(wèn)題模型可以表示為

值得說(shuō)明的是，以上模型可同時(shí)適用于快慢時(shí)間維波形設(shè)計(jì)。在雷達(dá)信號(hào)處理過(guò)程中，假設(shè)一個(gè)相參處理時(shí)間內(nèi)(Coherence Processing Interval,CPI)所包含的PRI為L(zhǎng)，一個(gè)PRI內(nèi)編碼xi長(zhǎng)度為N，X=[x1,x2,...,xL]∈CN×L為一個(gè)CPI內(nèi)發(fā)射信號(hào)，其中xi=[xi1,xi2,...,xiN]T∈CN×1為第i個(gè)PRI內(nèi)的相位編碼信號(hào)，而y=[x11,x21,...,xN1]∈C1×N是一個(gè)CPI內(nèi)所有PRI的初始相位編碼。對(duì)于快時(shí)間維波形設(shè)計(jì)模型，如前文所述，設(shè)計(jì)的發(fā)射波形為xi。而對(duì)于慢時(shí)間維波形設(shè)計(jì)，匹配濾波變?yōu)槁龝r(shí)間維匹配濾波，移位矩陣Jr中的參數(shù)r不再代表每個(gè)距離單元的移位，而是每個(gè)PRI對(duì)應(yīng)距離的移位，但仍可應(yīng)用本文的波形設(shè)計(jì)方法。

3 基于PML方法的模型求解

3.1 恒模約束下發(fā)射波形與接收濾波器設(shè)計(jì)

由于式(8)中包含兩個(gè)待優(yōu)化變量x和h，可采用一種交替迭代的優(yōu)化方法。將式(8)作如下簡(jiǎn)單變換：

其中，

對(duì)于確定性發(fā)射信號(hào)x，使目標(biāo)函數(shù)最大的h的最優(yōu)閉式解為[23]

對(duì)于固定h，最大化SINR對(duì)應(yīng)發(fā)射波形x可以通過(guò)如下方法求出。式(8)中的目標(biāo)函數(shù)可寫(xiě)成分式二次規(guī)劃形式：

其中，

式(12)是一個(gè)NP難的非凸優(yōu)化問(wèn)題，運(yùn)用類冪迭代方法可高效解決此類問(wèn)題[24]。

首先將問(wèn)題模型式(12)變?yōu)?/p>

P1的第2個(gè)約束條件可以等價(jià)變換為

其中，μ表示添加到原問(wèn)題P1的目標(biāo)函數(shù)的懲罰項(xiàng)的權(quán)重，當(dāng)μ→∞時(shí)，P2和P1完全相同。

將式(17)目標(biāo)函數(shù)寫(xiě)成關(guān)于x的二次函數(shù)形式，

其中，酉矩陣U是在不改變模長(zhǎng)的前提下將向量B1/2x旋轉(zhuǎn)到與A1/2x相同的方向，即式(19)成立：

將式(19)代入式(18)，易證問(wèn)題模型P3與P2等價(jià)。

通過(guò)求解式(19)，可以得到矩陣U，進(jìn)而可以求解問(wèn)題模型P3。對(duì)于酉矩陣U，直接求解式(19)不易，故可以將式(19)成立等效為等式左邊和右邊差值的二范數(shù)的平方最小，同時(shí)限制優(yōu)化變量U為酉矩陣。即求解U可等效于求解子問(wèn)題P4：

P4是只有正交約束的最小化問(wèn)題，優(yōu)化變量是矩陣U，其所在解空間集合稱為Stiefel流形，用符號(hào)表示[25]。對(duì)于P4，可以在流形空間St(n,r)上通過(guò)共軛梯度下降法求解。

求解子問(wèn)題P4得到酉矩陣U，對(duì)于確定的λ和U，P3可以看成一個(gè)二次規(guī)劃問(wèn)題，即

其中，

因此式(21)可以進(jìn)一步轉(zhuǎn)化為恒模二次規(guī)劃問(wèn)題：

求解式(24)即尋找式(25)問(wèn)題的最優(yōu)解[23]：

其中，式(25)的解是類冪迭代形式[16]：

arg(x)分別代表x的相位。關(guān)于類冪迭代方法對(duì)目標(biāo)函數(shù)的遞增性質(zhì)，文獻(xiàn)[23]已給出證明。

上述求解方法前提是給定λ和μ，下面給出參數(shù)λ和μ的確定方法。當(dāng)U與x確定時(shí)，P3問(wèn)題轉(zhuǎn)化為

根據(jù)簡(jiǎn)單求導(dǎo)運(yùn)算，易證上述二次優(yōu)化問(wèn)題的最優(yōu)解為

對(duì)于μ值，當(dāng)其滿足條件：

可以保證優(yōu)化式(27)的收斂性，達(dá)到收斂上界式(28)。

上文已說(shuō)明為保證問(wèn)題收斂性，μ的取值存在下界，同時(shí)μ的取值也不能過(guò)大。當(dāng)λ為定值，式(27)變?yōu)獒槍?duì)x的優(yōu)化問(wèn)題，由式(28)可知，優(yōu)化過(guò)程中，κ的取值應(yīng)趨近于λoptimal。但κ的取值恒小于λoptimal。故針對(duì)λ的優(yōu)化過(guò)程，κ的取值增大影響λoptimal增 大，λoptimal增大又趨使κ的上界繼續(xù)增大，直到收斂。且由式(28)可以看出，若μ過(guò)大，κ趨近于λoptimal的速度會(huì)變得緩慢，因此過(guò)大的μ會(huì)影響運(yùn)算速度。

根據(jù)上述過(guò)程，基于分式二次規(guī)劃的發(fā)射接收聯(lián)合互模糊函數(shù)賦形算法流程總結(jié)為算法1。其中，相鄰兩次迭代的內(nèi)外層迭代誤差分別記為 error1和error2 。外層迭代誤差 error1表達(dá)式為

其中，SINRupdate和 SINRbefore分別代表根據(jù)本次迭代和上次迭代所設(shè)計(jì)的發(fā)射波形與接收濾波器，所計(jì)算得到的回波SINR值。內(nèi)層迭代誤差表達(dá)式為

其中，xupdate和xbefore分別代表本次內(nèi)層迭代和上次內(nèi)層迭代所設(shè)計(jì)發(fā)射波形。

對(duì)算法1的計(jì)算復(fù)雜度進(jìn)行分析，由于所提算法采用迭代求解的方式，其總體計(jì)算復(fù)雜度是迭代次數(shù)的線性函數(shù)。假設(shè)Nr=Nh=N，在每一次迭代中，步驟3、步驟5-步驟8、步驟10的計(jì)算復(fù)雜度均為O(N3)。步驟4采用共軛梯度下降法，其計(jì)算復(fù)雜度與樣本數(shù)量、單個(gè)樣本計(jì)算量以及迭代次數(shù)有關(guān)。對(duì)U的求解式求導(dǎo)數(shù)：

在共軛梯度下降法的單次迭代中，其計(jì)算復(fù)雜度為O(N3)。因此，在每次外層迭代計(jì)算復(fù)雜度為O(N3)。

3.2 低PAR約束下發(fā)射波形與接收濾波器設(shè)計(jì)

考慮到發(fā)射信號(hào)的動(dòng)態(tài)范圍受硬件限制，例如功率放大器和A/D轉(zhuǎn)換器最大削波，通常希望發(fā)射信號(hào)具有低峰均比[1]。因此，3.2節(jié)將恒模約束放寬到低PAR約束，研究互模糊函數(shù)賦形方法。

發(fā)射信號(hào)的PAR可以定義為

對(duì)于低PAR約束下問(wèn)題的求解過(guò)程，前式推導(dǎo)大部分相同。僅PML內(nèi)層迭代式(25)變?yōu)?/p>

針對(duì)式(34)，可以引入文獻(xiàn)[26]中的最近鄰向量算法求解。具體算法流程如算法2所示。

4 仿真實(shí)驗(yàn)與實(shí)測(cè)數(shù)據(jù)實(shí)驗(yàn)結(jié)果分析

實(shí)施細(xì)節(jié)：為了驗(yàn)證所提方法的有效性和先進(jìn)性，本節(jié)從慢時(shí)間維波形優(yōu)化出發(fā)，通過(guò)數(shù)值仿真實(shí)驗(yàn)，對(duì)所提算法的收斂速度、運(yùn)行時(shí)間和SINR等性能進(jìn)行評(píng)估，并與文獻(xiàn)[15]中加權(quán)互模糊函數(shù)(Weighted-CAF,We-CAF)、文獻(xiàn)[17]中迭代最小化恒模模糊函數(shù)賦形(Unimodular AF Shaping via Iterative Minimization,UniAFSIM)，文獻(xiàn)[18]中序列迭代優(yōu)化算法(Iterative Sequential Optimization,ISO)以及文獻(xiàn)[23]中的認(rèn)知接收發(fā)射聯(lián)合設(shè)計(jì)循環(huán)算法(Cognitive Receiver and Waveform cyclic,CREWcyclic)等經(jīng)典算法進(jìn)行對(duì)比。本節(jié)的實(shí)驗(yàn)驗(yàn)證采用的初始化發(fā)射波形與接收濾波器均為隨機(jī)序列，并對(duì)5種不同的算法采用相同的隨機(jī)種子，使5種算法的初始發(fā)射波形完全相同。在本文所提算法中，內(nèi)外層誤差迭代值設(shè)置為ε1=1E-4,ε2=5E-4。仿真中涉及的關(guān)于計(jì)算時(shí)間的分析均在計(jì)算機(jī)(內(nèi)核2.30 GHz i7-12700H,RAM 16.0 GB)上進(jìn)行，MATLAB版本為R2022a。

算法 2 低PAR約束下最近鄰向量問(wèn)題求解方法Alg.2 Nearest vector method with low PAR

4.1 CM約束下互模糊函數(shù)賦形的仿真實(shí)驗(yàn)驗(yàn)證

其中，∪表示兩個(gè)集合的并集。

在實(shí)際問(wèn)題中干擾區(qū)域通常可以利用動(dòng)態(tài)環(huán)境數(shù)據(jù)庫(kù)來(lái)預(yù)測(cè)，例如地理信息系統(tǒng)、氣象數(shù)據(jù)、先前回波以及一些雜波譜模型等[10]。如前文問(wèn)題模型所述，將雜波的多普勒速度歸一化到目標(biāo)多普勒速度。因此對(duì)于本文仿真實(shí)驗(yàn)，目標(biāo)多普勒速度為vtarget=0。

圖2是式(12)中的目標(biāo)函數(shù)隨內(nèi)層迭代次數(shù)的變化曲線，可以看出響應(yīng)值呈階梯狀上升趨勢(shì)。如算法1所述，內(nèi)層迭代更新發(fā)射波形x，外層迭代更新接收濾波器h以及其他相關(guān)參數(shù)。圖2中局部放大圖為PML法更新發(fā)射波形對(duì)目標(biāo)響應(yīng)值的影響，即內(nèi)層迭代；而曲線整體趨勢(shì)代表更新接收濾波器對(duì)目標(biāo)響應(yīng)值的影響，即外層迭代。收斂曲線說(shuō)明本文所提方法使目標(biāo)函數(shù)響應(yīng)值單調(diào)遞增，且最終收斂到平穩(wěn)。

圖3對(duì)比了5種算法SINR值隨迭代次數(shù)的變化趨勢(shì)，其中外層迭代次數(shù)取前200次。本文所提算法、We-CAF,UniAFSIM,ISO算法以及CREWcyclic算法在經(jīng)過(guò)200次外層迭代后的SINR值分別為14.7 dB,5.1 dB,6.0 dB,10.3 dB和13.3 dB。可以看出，在200次外層迭代后，除了UniAFSIM和ISO算法，其余3種算法均達(dá)到收斂。在未達(dá)到收斂的兩種算法中，ISO算法在200次外層迭代后接近收斂，最終收斂為10.9 dB，而UniAFSIM算法尚未達(dá)到收斂，最終收斂值為11.5 dB。在5種算法中，本文所提算法和其余3種對(duì)比算法收斂所需外層迭代次數(shù)要明顯小于UniAFSIM算法的收斂所需外層迭代次數(shù)，且所提算法的收斂值要大于其余4種算法。4種算法中UniAFSIM方法收斂所需外層迭代次數(shù)較多，這是由于UniAFSIM是發(fā)射波形與接收濾波器相匹配的模糊函數(shù)設(shè)計(jì)，而本文所提算法、We-CAF以及ISO算法均改變接收濾波器，令其與發(fā)射波形失配，從而提高了波形設(shè)計(jì)的自由度，也提升了接收信號(hào)的SINR性能。

根據(jù)圖1所示的干擾能量分布圖，理想的互模糊函數(shù)圖應(yīng)該在干擾能量較大處具有較為明顯的凹陷，而在目標(biāo)所在的距離-多普勒單元具有較大響應(yīng)值，同時(shí)在雜波較低且不存在目標(biāo)的區(qū)域平均分配能量。圖4是5種不同算法設(shè)計(jì)發(fā)射波形與接收濾波器的互模糊函數(shù)圖。互模糊函數(shù)的計(jì)算方法為

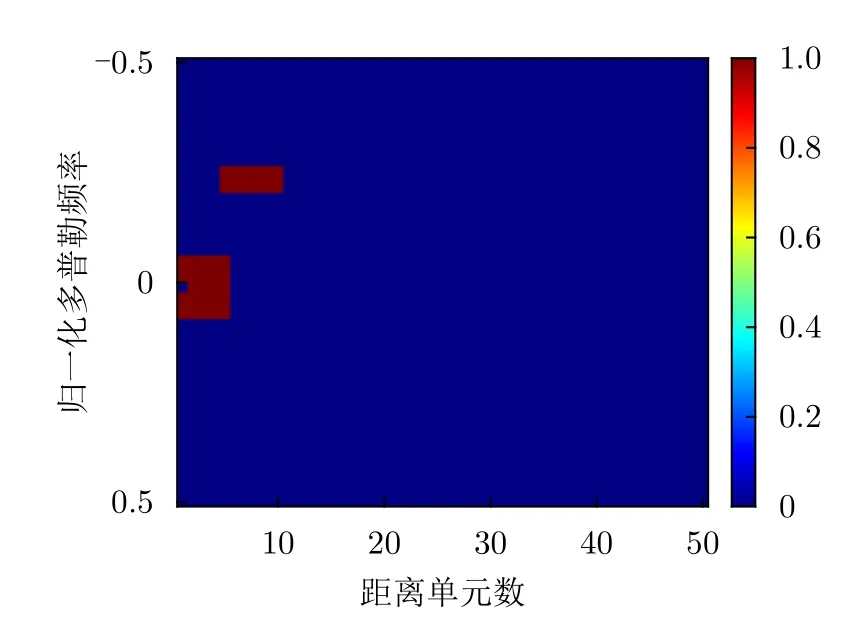
圖1 干擾能量分布Fig.1 Interference energy distribution

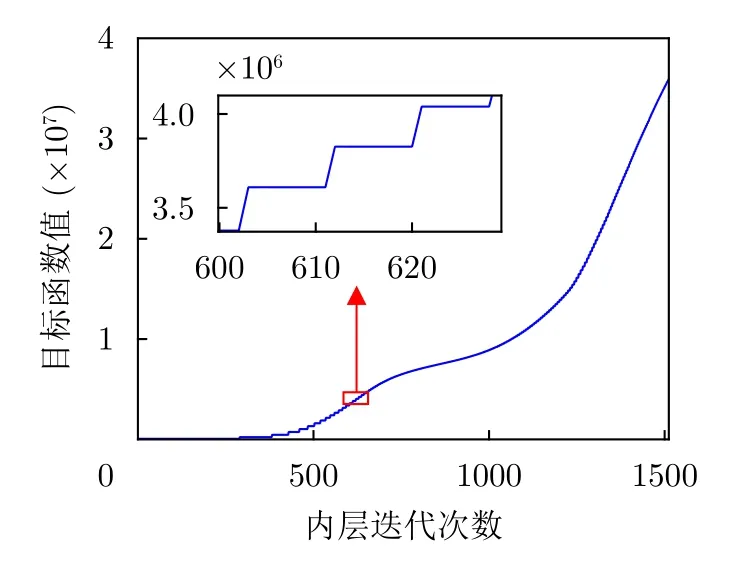
圖2 本文算法目標(biāo)函數(shù)響應(yīng)值收斂曲線Fig.2 The convergence curve of objective function response value in the proposed algorithm

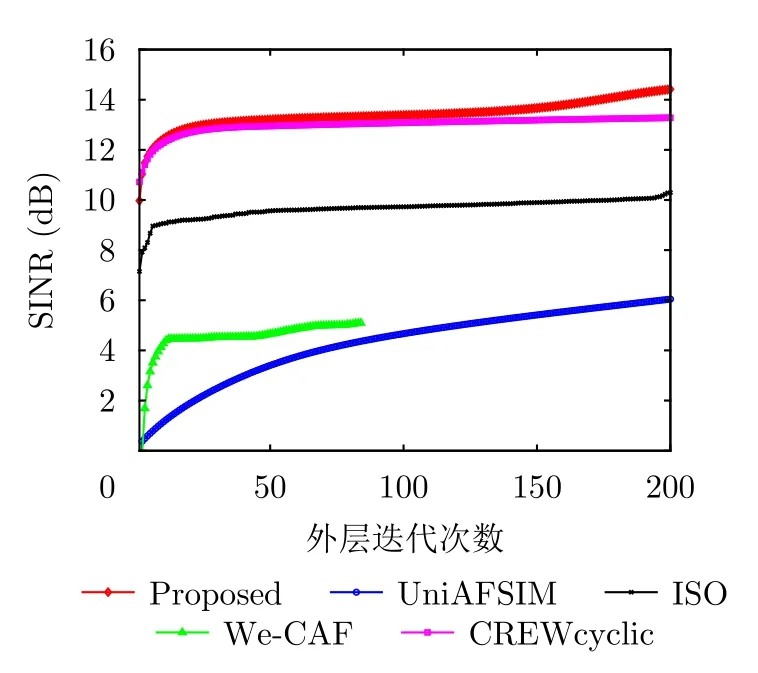
圖3 不同方法下SINR值隨迭代次數(shù)變化Fig.3 SINR versus the iteration times of different algorithms

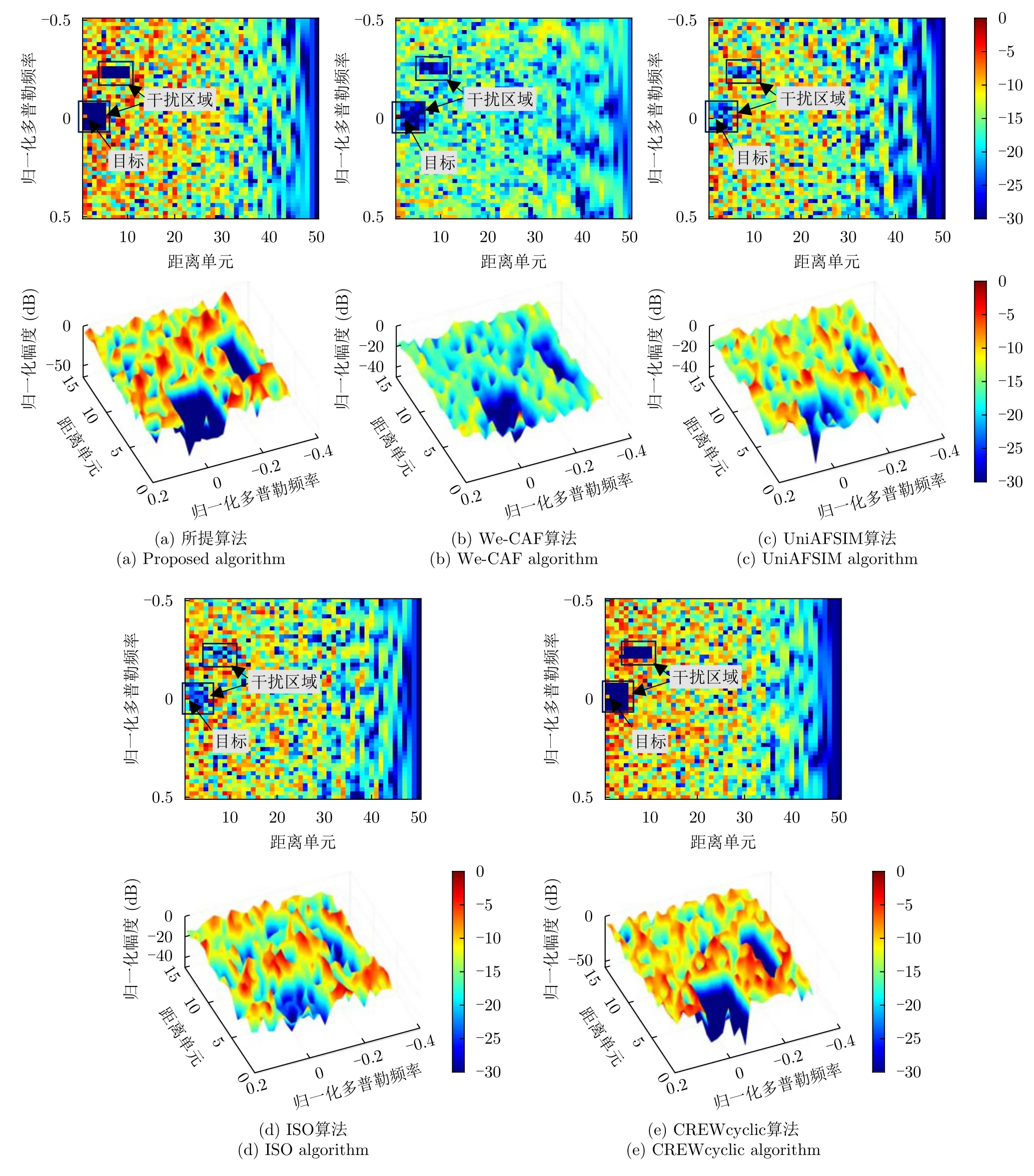
圖4 5種算法生成CAFFig.4 CAF generated by five different algorithms

其中，圖4框內(nèi)是雜波所在的距離-多普勒單元，圖4的互模糊函數(shù)在雜波所處距離單元內(nèi)均具有凹口，證明了5種算法的有效性。從圖4可以看出，本文所提CM約束下的聯(lián)合設(shè)計(jì)方法與CREWcyclic算法設(shè)計(jì)發(fā)射與接收濾波器具有較好的互模糊函數(shù)性能。

圖5展示了圖4在距離單元為r=1,2,3的截面圖，其中紅色區(qū)域?yàn)楦蓴_能量分布集中處，r=1,h=0為目標(biāo)所在距離-多普勒單元。從圖5可以看出，歸一化多普勒頻率在 [-0.06,0.06]時(shí)，即雜波干擾集中處，5種方法對(duì)不同的距離單元均有較為明顯的凹口和尖峰。對(duì)于目標(biāo)附近雜波區(qū)域的CAF凹陷深度，We-CAF,UniAFSIM,ISO算法旁瓣大小可以達(dá)到約-30 dB，CREWcyclic算法在r=1,2,3的距離單元處的凹陷均可達(dá)到-40 dB，而本文所提算法凹陷值可達(dá)到約-50 dB。因此本文所提算法和CREWcyclic算法相比于其他3種算法在多普勒維度，具有更低的旁瓣。

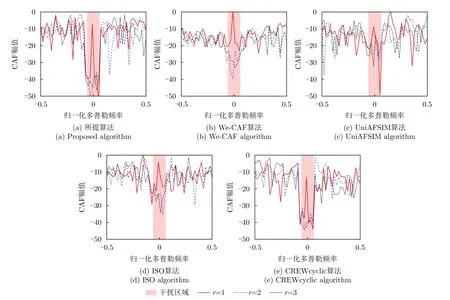
圖5 5種算法生成CAF距離單元(r=1,2,3;N=50)截面圖Fig.5 Distance cut (r=1,2,3) of the CAF generated by five algorithms (N=50)

為了進(jìn)一步體現(xiàn)所提方法在不同碼長(zhǎng)下的性能與運(yùn)行效率，改變發(fā)射波形碼長(zhǎng)為N=30:10:100，并對(duì)比5種算法接收回波的SINR值和達(dá)到收斂時(shí)的運(yùn)行時(shí)長(zhǎng)。從表1可以看出，隨著發(fā)射波形碼長(zhǎng)的增加，5種算法達(dá)到收斂的時(shí)間均增加。其中所提方法與CREWcyclic方法程序運(yùn)行時(shí)長(zhǎng)相近，且CREWcyclic算法運(yùn)行效率略優(yōu)于所提算法。Uni-AFSIM算法和ISO算法的運(yùn)算時(shí)長(zhǎng)明顯增大，在運(yùn)行效率上要略差于其他3種算法。We-CAF算法達(dá)到收斂的速度較快，這是由于We-CAF算法未對(duì)發(fā)射波形進(jìn)行恒模約束。所提算法運(yùn)行時(shí)長(zhǎng)略高于CREWcyclic算法的原因在于，在優(yōu)化求解方式上，兩者均利用內(nèi)外兩層迭代交替更新發(fā)射波形與接收濾波器，但在將分式規(guī)劃轉(zhuǎn)化到二次規(guī)劃的過(guò)程中，CREWcyclic采用Dinkelbach算法，而本文通過(guò)引入新的參數(shù)λ,μ,U，將約束條件與目標(biāo)函數(shù)進(jìn)行轉(zhuǎn)化，把問(wèn)題分式規(guī)劃形式變換到二次規(guī)劃形式。在本文的轉(zhuǎn)化方式中采用了共軛梯度下降法，這導(dǎo)致運(yùn)行時(shí)長(zhǎng)的增加，因此所提方法較CREWcyclic算法運(yùn)算效率低。同時(shí)，圖6表明本文設(shè)計(jì)發(fā)射波形和接收濾波器下，回波的SINR性能相較于其余4種方法有明顯提升。雖然本文所提算法和CREWcyclic均在雜波所在的距離-多普勒單元具有較低的凹口，但CREWcyclic算法生成的發(fā)射波形與接收濾波器在對(duì)回波進(jìn)行處理后，SINR值低于本文算法。其原因可由圖5(e)看出，CREWcyclic算法對(duì)應(yīng)發(fā)射波形-接收濾波器對(duì)目標(biāo)所在零多普勒點(diǎn)的非匹配濾波響應(yīng)值不高，即峰值SINR值損失較大。另外，本文所提方法和CREWcyclic算法由于目標(biāo)函數(shù)為接收SINR最大化，因此忽略了非匹配接收帶來(lái)的峰值SINR損失，這也可作為未來(lái)工作的發(fā)展方向。

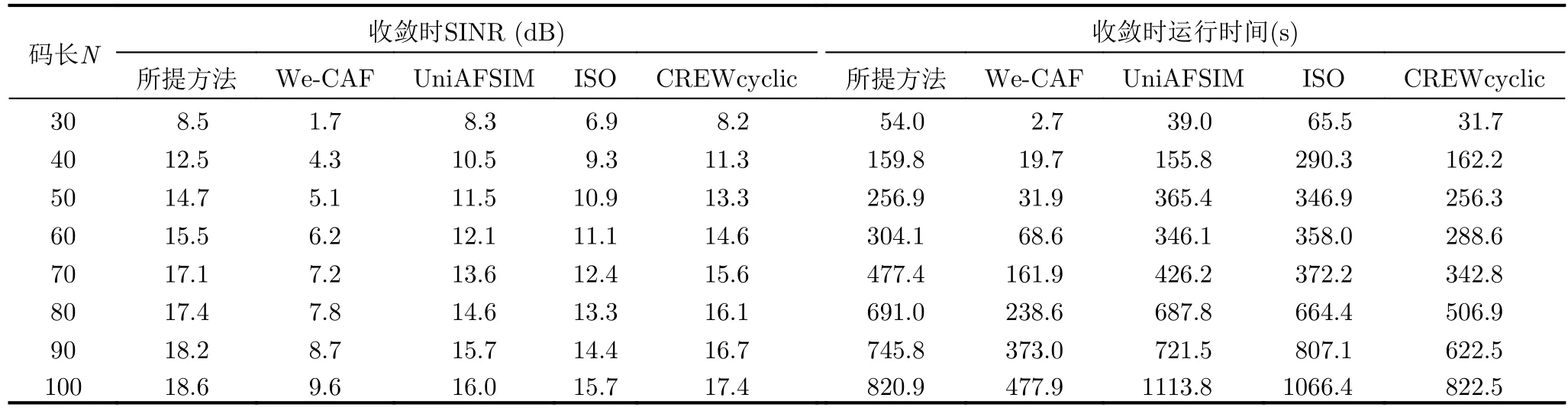
表1 不同碼長(zhǎng)下5種算法性能統(tǒng)計(jì)Tab.1 Performance statistics table of five algorithms under different code length

4.2 低PAR約束下互模糊函數(shù)賦形的實(shí)驗(yàn)驗(yàn)證

當(dāng)把CM約束放寬到低PAR約束時(shí)，利用最近鄰向量法所設(shè)計(jì)的發(fā)射波形的實(shí)部與虛部如圖7所示。當(dāng) PAR=1時(shí)，本文產(chǎn)生的發(fā)射波形所對(duì)應(yīng)的點(diǎn)位于單位圓上，證明產(chǎn)生的發(fā)射波形滿足CM約束。當(dāng) PAR=2 時(shí)，點(diǎn)的分布半徑較 PAR=1相對(duì)分散，但也滿足PAR約束。這說(shuō)明PAR值越大，波形幅度起伏越大，越不利于實(shí)際應(yīng)用。值得說(shuō)明的是，由于h僅在接收機(jī)中使用，無(wú)需滿足峰均比的硬件約束，本文并未對(duì)其模長(zhǎng)做任何約束，這與文獻(xiàn)[15]的思路是一致的。

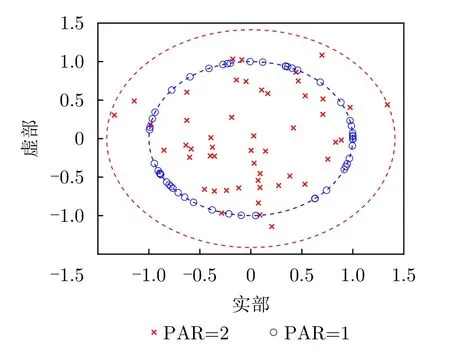
圖7 不同PAR約束下發(fā)射波形實(shí)部虛部Fig.7 The real and imaginary parts of transmitting waveform under different PAR constraints

對(duì)發(fā)射序列選取不同的PAR值作為約束條件，圖8展示了恒模約束、PAR=2,PAR=4條件下，SINR性能隨外層迭代次數(shù)的變化曲線。在1000次外層迭代下，3種約束下所能達(dá)到的SINR值分別為14.7 dB,15.5 dB以及16.0 dB。可以看出隨著PAR約束的逐漸放寬，發(fā)射波形與接收濾波器具有更好的SINR性能。這是由于隨著PAR值變大，發(fā)射波形的可行解域也變大，所以最終收斂值也會(huì)相應(yīng)變大。

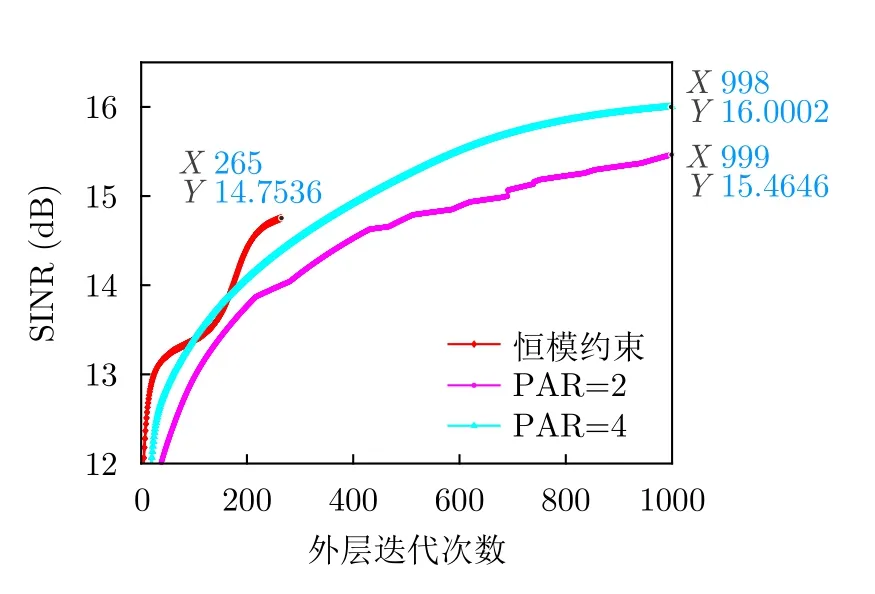
圖8 不同PAR約束下SINR值隨運(yùn)行時(shí)間變化Fig.8 SINR versus the iteration time under different PAR constraints

4.3 互模糊函數(shù)賦形的超參數(shù)分析

本小節(jié)將對(duì)模型求解中給出的μ,κ,λ這3種參數(shù)取值規(guī)律提出數(shù)值仿真實(shí)驗(yàn)證明。由上文分析，為了增大收斂速度，可使3者均隨著外層迭代變化直至收斂。在實(shí)驗(yàn)中，設(shè)置

其中，k為可變參數(shù)。

令k=1/5,2,5,10 分別在碼長(zhǎng)N=50條件下實(shí)驗(yàn)，外層迭代次數(shù)控制在300次，結(jié)果如圖9所示。可以看出，在外層迭代次數(shù)達(dá)到300次時(shí)，僅k=2 時(shí)算法達(dá)到收斂。實(shí)驗(yàn)證明，當(dāng)k＞1時(shí)，隨著k取值的增大，算法收斂速度逐漸變慢；當(dāng)k＜1時(shí)，即不滿足式(29)所示條件時(shí)，算法不收斂。因此，在應(yīng)用本文所提算法時(shí)，需綜合考慮算法收斂性能和運(yùn)行速度，選擇合適的k參數(shù)。本文實(shí)驗(yàn)均在k=2條件下進(jìn)行。

圖9 不同k取值下信干噪比隨運(yùn)行時(shí)間變化曲線Fig.9 SINR with respect to running time under different values of k

4.4 CM約束下互模糊函數(shù)賦形的實(shí)測(cè)數(shù)據(jù)驗(yàn)證

上文的仿真實(shí)驗(yàn)僅對(duì)雜波分布進(jìn)行簡(jiǎn)單的塊狀假設(shè)，為了分析實(shí)際場(chǎng)景中雜波在RD圖上的分布形狀，本節(jié)將利用實(shí)測(cè)數(shù)據(jù)作為雜波先驗(yàn)信息，測(cè)試本文算法在更為復(fù)雜場(chǎng)景下的性能。本節(jié)采用海南地區(qū)近岸海雜波前下視掛飛實(shí)測(cè)數(shù)據(jù)作為實(shí)驗(yàn)場(chǎng)景，對(duì)本文算法進(jìn)行分析。采集實(shí)測(cè)數(shù)據(jù)時(shí)，相關(guān)雷達(dá)參數(shù)如表2所示。取回波的前64個(gè)脈沖數(shù)據(jù)做距離-多普勒?qǐng)D分析，并在距離維截取前64個(gè)距離單元，結(jié)果如圖10所示。紅色區(qū)域即為雜波干擾集中區(qū)域，其所在歸一化多普勒頻率區(qū)間為[-0.15,0.20]。

表2 實(shí)測(cè)數(shù)據(jù)實(shí)驗(yàn)下的雷達(dá)參數(shù)Tab.2 Radar parameters in real measured data experiment

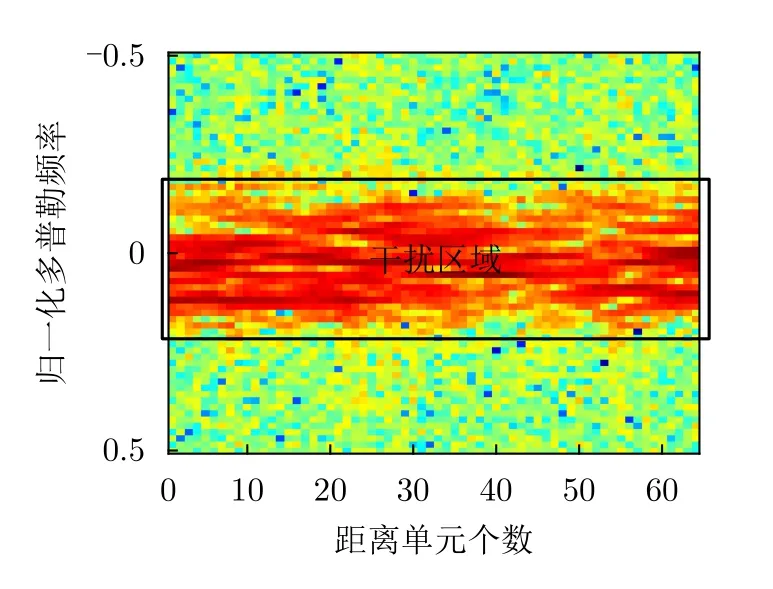
圖10 海南地區(qū)某機(jī)場(chǎng)實(shí)測(cè)數(shù)據(jù)距離-多普勒?qǐng)DFig.10 Range-Doppler diagram of real measured data from an airport in Hainan

利用算法1對(duì)圖10所示干擾區(qū)域進(jìn)行恒模發(fā)射波形-接收濾波器設(shè)計(jì)。所得SINR隨迭代次數(shù)變化趨勢(shì)如圖11(a)所示，算法對(duì)于實(shí)測(cè)數(shù)據(jù)滿足單調(diào)收斂趨勢(shì)，并且收斂值可達(dá)17.1 dB。本文算法所設(shè)計(jì)的發(fā)射波形與接收濾波器的幅度和相位信息如圖11(c)、圖11(d)所示，雖然所提方法并未對(duì)接收濾波器進(jìn)行幅度約束，但結(jié)果表明其幅度差別不大，具備實(shí)際應(yīng)用可能。生成的CAF如圖11(b)所示，其形狀在對(duì)應(yīng)的雜波分布較為集中的距離-多普勒區(qū)域具有凹陷，這證明了所提算法在更復(fù)雜場(chǎng)景下的有效性。

圖11 實(shí)測(cè)數(shù)據(jù)運(yùn)用算法1運(yùn)行結(jié)果Fig.11 Results of applying Alg.1 to the real measured data

5 結(jié)語(yǔ)

針對(duì)經(jīng)典CAF賦形方法中，波形對(duì)微弱運(yùn)動(dòng)目標(biāo)的檢測(cè)能力不高，且運(yùn)算效率較低的問(wèn)題，本文分別以CM和低PAR為約束條件，提出了一種基于最大化SINR優(yōu)化準(zhǔn)則的發(fā)射波形與接收濾波器互模糊函數(shù)賦形方法。為了解決所建模的恒模二次分式非凸優(yōu)化問(wèn)題，先將其轉(zhuǎn)化為恒模二次規(guī)劃問(wèn)題，并利用交替迭代與PML方法求得最優(yōu)解。仿真與實(shí)測(cè)雜波數(shù)據(jù)下的實(shí)驗(yàn)證明，相比于現(xiàn)有方法，本文具有更高的SINR和短碼長(zhǎng)下較高運(yùn)算效率，同時(shí)可以實(shí)現(xiàn)任意PAR約束下的聯(lián)合設(shè)計(jì)。另外，本文還驗(yàn)證了算法中超參數(shù)取值對(duì)收斂性能與迭代速度的影響，以期對(duì)算法實(shí)際應(yīng)用中的參數(shù)選擇提供理論依據(jù)與經(jīng)驗(yàn)參考。基于本文研究，未來(lái)的工作可集中于以下兩部分，一是在問(wèn)題模型中考慮增加峰值SINR損失約束，以解決強(qiáng)噪聲背景下的目標(biāo)檢測(cè)問(wèn)題；二是完善外場(chǎng)實(shí)驗(yàn)方案，通過(guò)發(fā)射波形設(shè)計(jì)和相應(yīng)的接收回波處理，在實(shí)際復(fù)雜場(chǎng)景下驗(yàn)證所提算法的有效性。

利益沖突所有作者均聲明不存在利益沖突

Conflict of InterestsThe authors declare that there is no conflict of interests