空間微動多目標雙基地雷達回波仿真方法

關鍵詞：微動；多目標；雙基地雷達；回波仿真

中圖分類號：ＴＮ９５５ 文獻標志碼：Ａ DOI：１０．１２３０５／ｊ．ｉｓｓｎ．１００１-５０６Ｘ．２０２４．１２．０８

０引言

空間目標在突防時，常使用誘餌釋放、彈頭分導和協同打擊等多種突防手段，使得反導雷達常常面臨多目標環境。相對于單目標，多目標探測與識別往往更為困難。一方面，密集多目標往往集中在同一雷達波束內，低分辨雷達單從距離向和方位向難以實現目標分離［１］；另一方面，各目標運動參數不一致，使得雷達成像時的運動補償更加困難［２３］，許多問題有待于深入研究。

空間目標由于空氣擾動存在著旋轉、進動和章動等微動形式［４］，利用微動特征進行目標分類和識別已成為反導雷達的關鍵技術［５６］。對于距離分辨力較弱的窄帶雷達而言，利用微動特征進行目標分辨成為了一條可行的途徑［７］，但多目標微動分量的相互交叉為微動特征提取帶來了挑戰［８］。文獻［９］使用復雜獨立成分分析的方法對彈頭、誘餌的混合回波進行分離，有效避免了時頻分析中交叉項的影響。文獻［１０］從時頻分析算法入手，利用深度學習的方法，在保持曲線高分辨的條件下，有效消除了曲線間的交叉項。文獻［１１］將非對稱Ｆｅｒｇｕｓｏｎ參數模型與Ｈｏｕｇｈ變換相結合，解決了在多目標時頻曲線跟蹤中的頻率交叉問題。文獻［１２］利用高階模糊函數、延遲共軛相乘及時頻分布處理相結合的方法，能夠在不分離信號的前提下完成多目標平動參數和微動周期的估計。文獻［１３］使用二元Ｈｏｕｇｈ變換和自適應時頻濾波的方法，在大目標散射能量較大的場景下，同時完成了大目標和小目標的檢測。文獻［１４］將微多普勒曲線視為高階馬爾可夫鏈的狀態模型，利用“檢測前跟蹤”的方法完成了具有平動的微動曲線的提取，具有較強的抗噪性能。文獻［１５］充分利用分量間的關系，對提取的時頻脊線重新分配，解決了多條時頻曲線提取時的脊線失配問題。上述文獻均針對單基地雷達，而單基地雷達面臨強干擾和被摧毀的威脅。

雙基地雷達具有天然的“四抗”優勢［１６］，在防空反導體系逐漸得到應用，對空間微動目標探測與識別具有重要意義。文獻［１７］推導了空間錐形目標散射中心的位置，重構出了微動目標的雙基地雷達一維距離像，并總結了一維距離像與目標長度的關系。文獻［１８］基于窄帶發／收收（ｔｒａｎｓｍｉｔｔｅｒ／ｒｅｃｅｉｖｅｒ-ｒｅｃｅｉｖｅｒ，Ｔ／Ｒ-Ｒ）的雙基地雷達體制，提出了一種空間旋轉目標的成像方法。文獻［１９］研究了基于寬帶復合雙基地雷達空間自旋目標三維成像方法。但雙基地雷達多目標的微動成像與特征提取鮮見報道，難以獲得有效的雙基地微動多目標回波數據是一個重要因素。由于實測數據的保密性，空間多目標的研究往往由回波仿真生成數據，回波模型的逼真度在一定程度上影響了特征提取方法研究的正確性。在高頻區，目標回波可以等效視為若干散射中心回波的疊加［２０］，空間錐形目標由錐頂局部型散射中心（ｌｏｃａｌｉｚｅｄｓｃａｔｔｅｒｉｎｇｃｅｎｔｅｒ，ＬＳＣ）和錐底邊緣滑動型散射中心（ｓｌｉｄｉｎｇｓｃａｔｔｅｒｉｎｇｃｅｎｔｅｒｓｏｆｔｈｅｅｄｇｅ，ＳＳＣＥ）［２１］組成。文獻［１２］在特征提取中考慮了這兩類散射中心的參數化模型，但回波仿真僅針對單基地雷達。文獻［９］利用電磁計算，使用全波法獲得了多個微動目標的單基地混合回波，得到了更為精準的模型，但考慮的目標均為同一尺寸的錐體目標，對于存在相對運動、尺寸不同、入射和散射方向不同的情形，電磁計算時間成本巨大。

為此，本文聚焦于雙基地雷達探測中微動多目標的回波仿真問題，基于散射中心模型建立了微動多目標的雙基地雷達動態回波仿真模型。對仿真的窄帶回波進行微多普勒特征提取與分析，對寬帶回波進行一維像特征和二維像特征提取與分析，并通過電磁計算結果驗證了模型的正確性。

３動態仿真與驗證

３．１窄帶回波動態仿真與分析

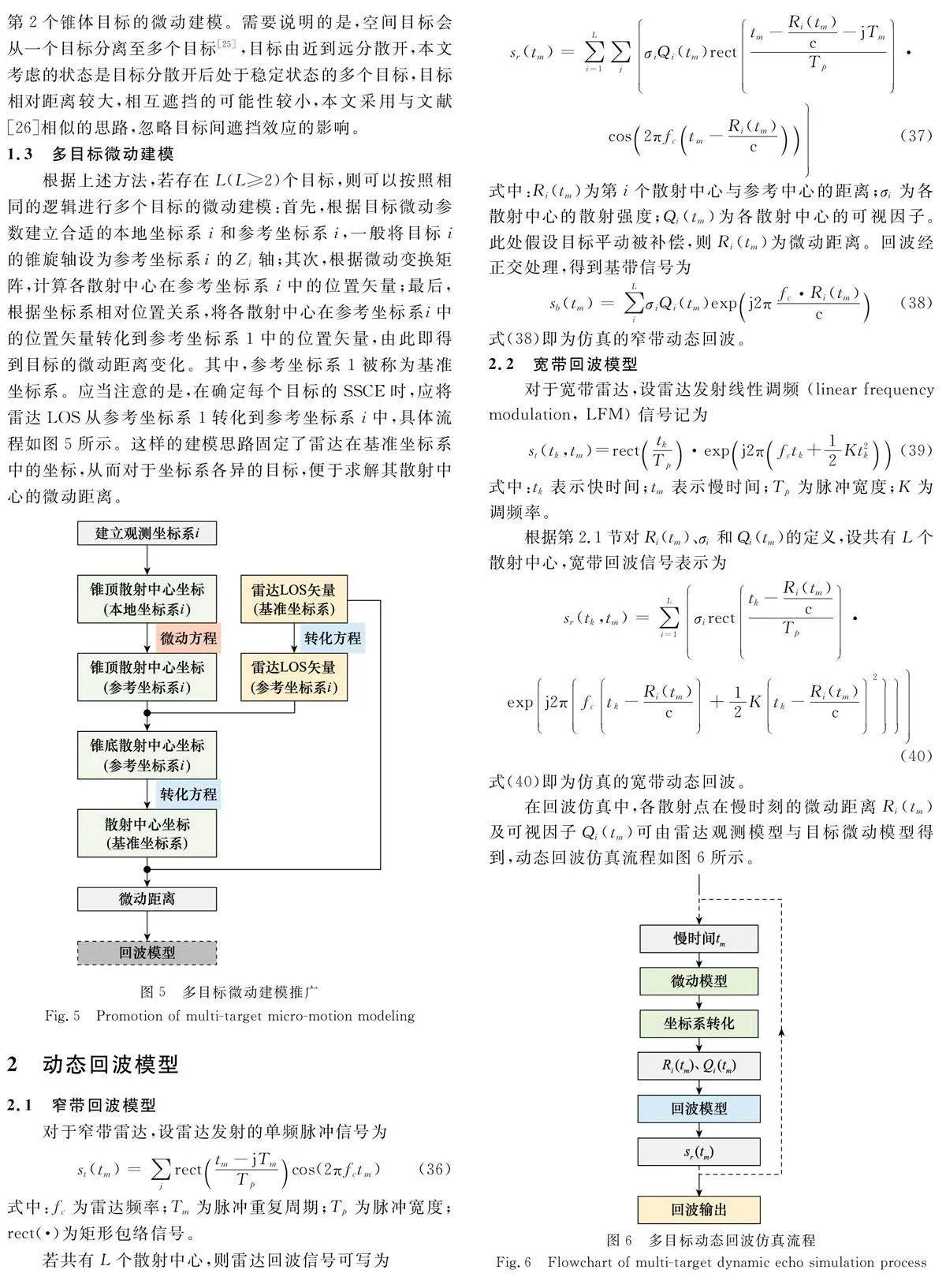
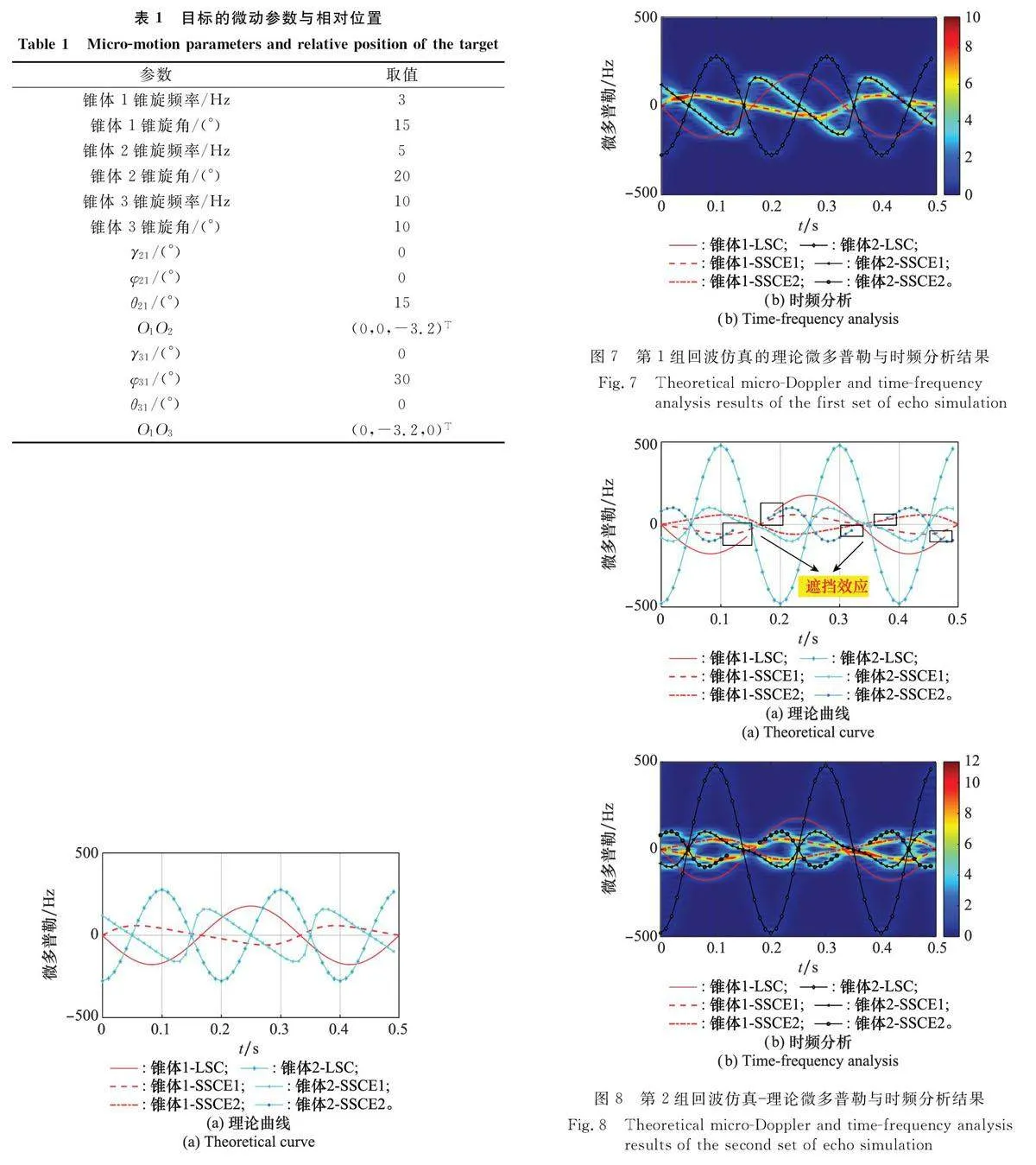
設置雷達頻率為５ＧＨｚ，脈寬T_P＝１０μｓ，脈沖重復周期為T_m＝１ ｍｓ，發射信號為單頻信號，入射ＬＯＳ 和接收ＬＯＳ的方位角均為９０°。在仿真中，３ 個目標均為半徑為０．５ｍ、高度為１．６ ｍ 的錐形目標，ＬＳＣ 散射強度與ＳＳＣＥ散射強度之比為１∶１０［２７］，每個目標包含３ 個散射中心，根據可視條件判斷是否出現在回波信號中。目標其他微動參數與位置關系如表１所示。

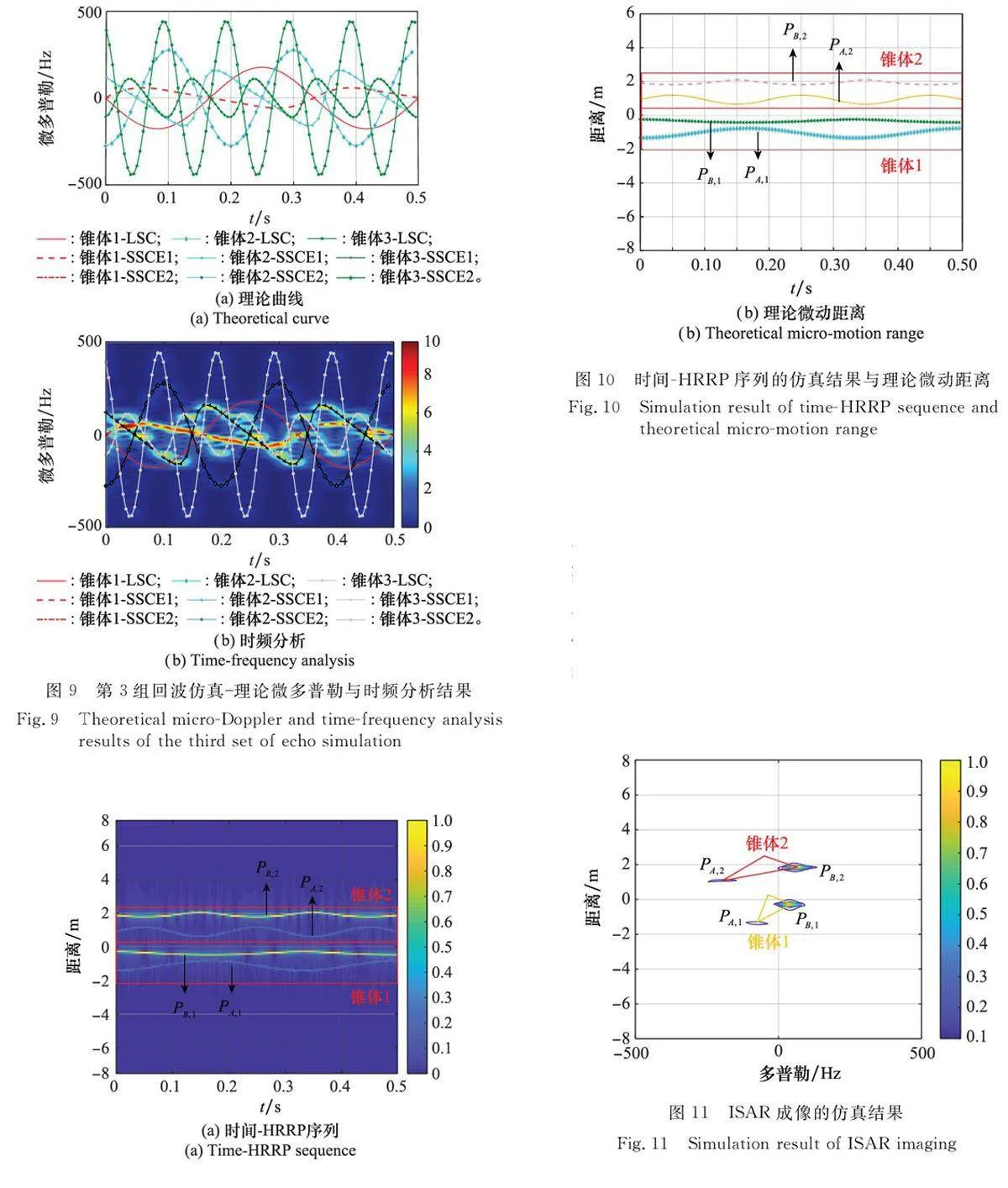
下面進行３ 組仿真分析，第１ 組仿真錐體１ 和錐體２的回波，入射ＬＯＳ和接收ＬＯＳ的俯仰角分別為３０°和６０°。對回波進行短時傅里葉變換（ｓｈｏｒｔｔｉｍｅＦｏｕｒｉｅｒｔｒａｎｓ-ｆｏｒｍ，ＳＴＦＴ），理論微多普勒曲線和回波仿真的時頻圖如圖７ 所示。圖例中，ＳＳＣＥ１ 表示靠近雷達端的ＳＳＣＥ，ＳＳＣＥ２表示遠離雷達端的ＳＳＣＥ，下文無特殊說明均為此。第２組仍仿真錐體１和錐體２的回波，但改變入射ＬＯＳ和接收ＬＯＳ的俯仰角分別為１２０°和１５０°，理論結果與仿真結果如圖８ 所示。第３ 組仿真３個目標的回波，設置入射ＬＯＳ和接收ＬＯＳ的俯仰角分別為３０°和６０°，理論結果與仿真結果如圖９所示。

觀察圖７、圖８和圖９的結果，回波仿真的微多普勒曲線與理論曲線一致，證明了回波能夠準確表示由各散射中心運動引起的相位變化。值得注意的是，在第１組和第３組仿真中，錐體目標遠離雷達端的ＳＳＣＥ 在觀測時間內均被遮擋，而在第２組仿真中，錐體１ 的ＬＳＣ 和錐體２ 的ＳＳＣＥ 出現了短暫被遮擋的現象。在其他時間內，錐體目標的３ 個散射中心均能被觀察到，回波仿真結果也正確體現了遮擋效應。

３．２寬帶回波動態仿真與分析

設置雷達發射信號為載頻為５ＧＨｚ、帶寬為２ＧＨｚ的ＬＦＭ 信號，其他參數保持不變。在仿真中，錐體微動參數與雷達視線與第１組窄帶仿真參數設置一致。對回波進行Ｄｅｃｈｉｒｐ處理［２８］，得到目標能量歸一化后的一維高分辨距離像（ｈｉｇｈｒｅｓｏｌｕｔｉｏｎｒａｎｇｅｐｒｏｆｉｌｅ，ＨＲＲＰ）序列，如圖１０（ａ）所示，仿真中散射中心的理論微動距離變化如圖１０（ｂ）所示。

由圖１０可以觀察到，由于寬帶雷達的高分辨率，經脈沖壓縮處理后，一維ＨＲＲＰ序列出現了跨越距離單元的現象，并呈周期變化，不同目標的散射中心呈現不同的進動周期。得到的一維ＨＲＲＰ 序列與散射中心的理論微動距離變化一致。同時，由于遠離雷達端的ＳＳＣＥ 被遮擋，兩個錐體均有兩個明顯的散射中心。

利用目標的高速微動可以進一步得到逆合成孔徑雷達（ｉｎｖｅｒｓｅｓｙｎｔｈｅｔｉｃａｐｅｒｔｕｒｅｒａｄａｒ，ＩＳＡＲ）成像［２９］。仿真中，利用距離瞬時多普勒（ｒａｎｇｅｉｎｓｔａｎｔａｎｅｏｕｓＤｏｐｐｌｅｒ，ＲＩＤ）成像算法［３０］，得到目標能量歸一化后的二維像，如圖１１ 所示。從圖中可以觀察到４ 個特顯點，分別對應兩個錐體目標的４個散射中心。但由于兩個目標的轉動角速度不同，成像得到的目標尺寸也不相同。

３．３電磁計算數據驗證

３．３．１窄帶電磁計算結果

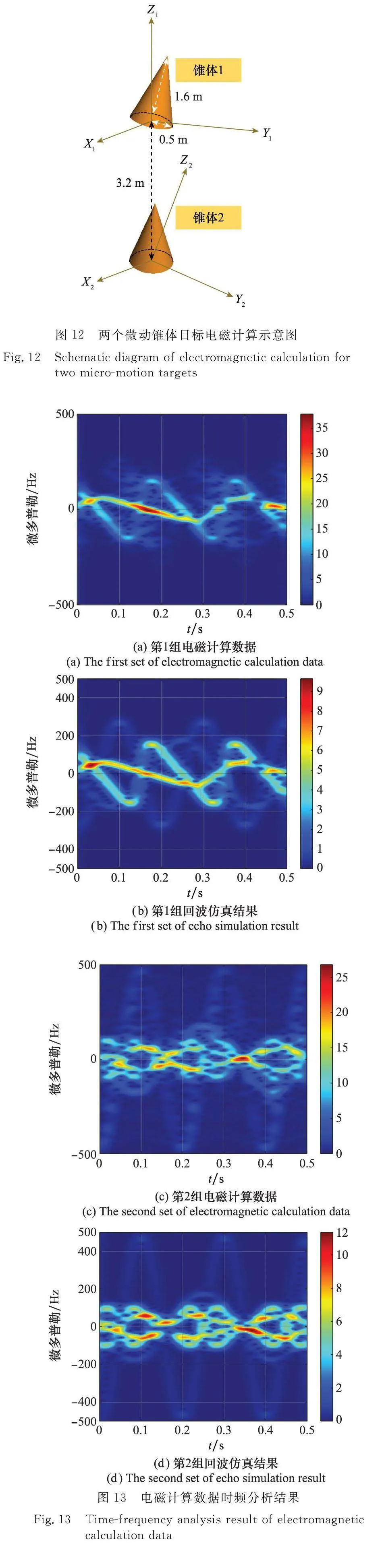
使用商業電磁計算軟件ＦＥＫＯ計算第１組窄帶回波仿真和第２組回波仿真中在兩個錐體目標情形下的動態電磁數據，同時對電磁計算數據進行時頻分析。其中，電磁計算算法設置為矩量法（ｍｅｔｈｏｄｏｆｍｏｍｅｎｔｓ，ＭｏＭ），參數設置與回波仿真設置保持一致，電磁計算示意圖如圖１２所示。在電磁計算過程中，首先給定某一慢時間時刻，通過微動方程計算各目標在該時刻下的微動姿態，然后通過電磁計算軟件生成特定姿態下的錐體目標，再給定雷達頻率和ＬＯＳ角，并計算電磁計算數據，最后將電磁計算數據按照觀測時間順序排列，得到微動目標的動態電磁數據。

對動態電磁計算數據進行時頻分析，結果如圖１３（ａ）和圖１３（ｃ）所示，圖１３（ｂ）和圖１３（ｄ）分別給出了相應的回波仿真結果。通過對比圖１３（ａ）和圖１３（ｂ）以及圖１３（ｃ）和圖１３（ｄ），可以發現，目標ＳＳＣＥ 能量較強，微多普勒曲線明顯，仿真結果與電磁計算結果一致。而ＬＳＣ 由于能量較弱，在電磁計算結果中與其他弱能量相互交叉，并不明顯，但仍能夠看到較為清晰的微多普勒曲線，與仿真結果一致。

電磁計算結果中部分弱能量出現的原因是目標強散射中心的能量并不能完全包含整個目標的能量，點散射中心回波模型只是近似的結果，但當仿真回波用于微動特征提取時，不被散射中心包含的能量非常小，且不影響散射中心的微多普勒曲線，可以忽略。同時，如圖１３（ｃ）所示，在電磁計算中，散射中心強度隨姿態角小幅變化，使得微動曲線能量隨時間變化，加之微動曲線相互交叉，使得時頻圖中微動曲線不連續，這在回波仿真中也能夠體現。

采用矩陣相關系數和圖像誤差進一步定量說明仿真結果和電磁計算結果的相似性和差異性。兩個矩陣的相關系數定義為二值矩陣；犕和犖分別為矩陣的行數和列數。

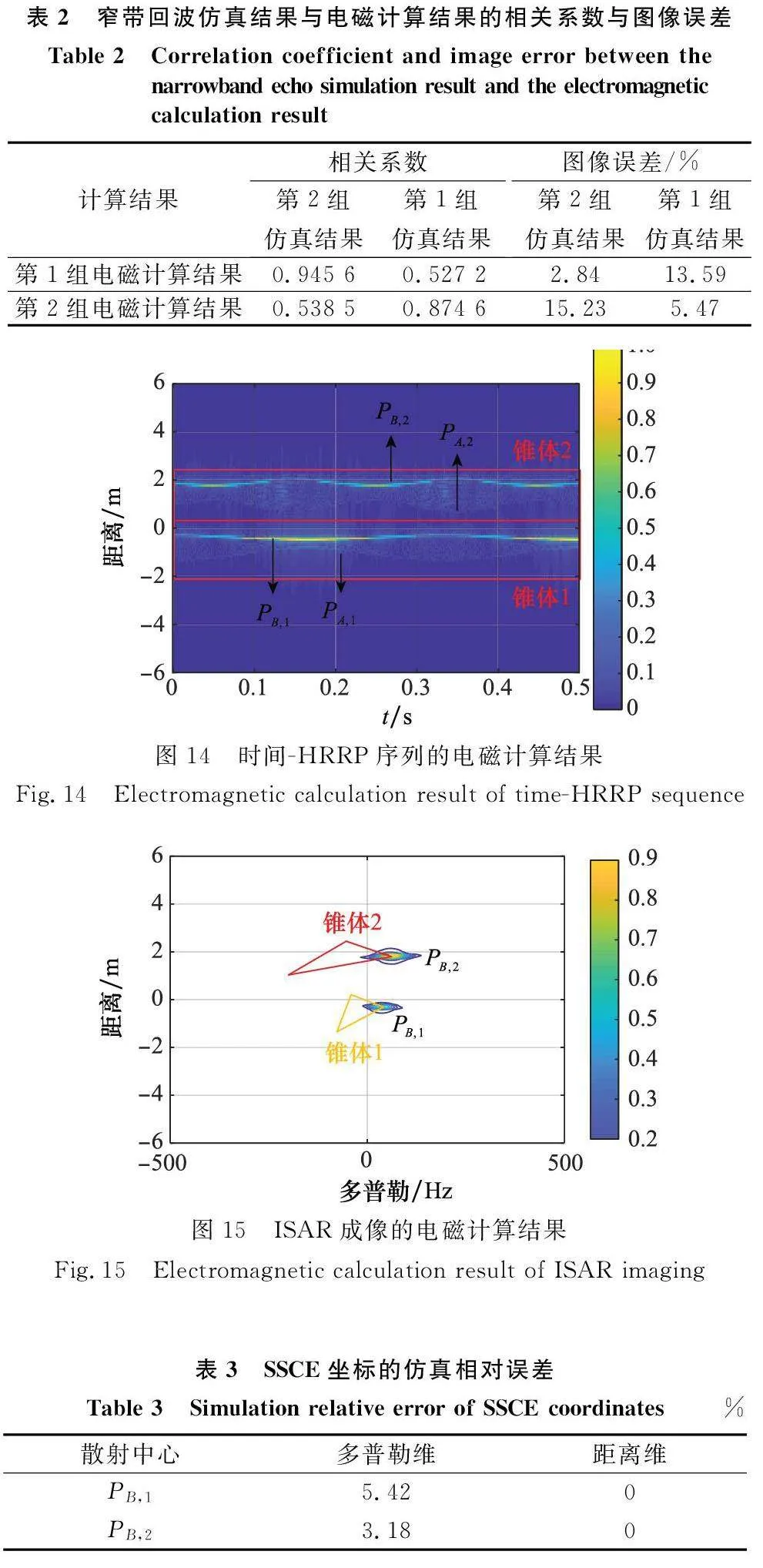
將兩組仿真結果和電磁計算結果歸一化后，兩兩計算相關系數和圖像誤差，結果如表２所示。結果顯示，兩組仿真結果和電磁計算結果的相關系數均大于０．８５，具有很好的相似性，且圖像誤差小于６％，圖像的差異性較小，進一步說明了仿真結果的有效性。需要說明的是，由于微動矩陣是一個零值較多的稀疏矩陣，所以第１組仿真結果與第２組電磁計算結果的圖像誤差值不大，接近１５％，反之亦然。

３．３．２寬帶電磁計算結果

采用ＦＥＫＯ 中的物理光學（ｐｈｙｓｉｃａｌｏｐｔｉｃｓ，ＰＯ）近似算法計算寬帶回波仿真情形下的掃頻數據，其等效為快時間域基帶回波［３１］。采用與第３．３．１節相同的方法，得到微動目標的動態電磁數據。對回波在快時間域進行傅里葉變換（Ｆｏｕｒｉｅｒｔｒａｎｓｆｏｒｍ，ＦＴ），得到目標的時間-ＨＲＲＰ序列，結果如圖１４所示。利用ＲＩＤ 成像算法，以與仿真相同的觀測時間對目標進行二維成像，結果如圖１５所示。

觀察圖１０ 與圖１４ 結果，電磁計算數據得到的時間-ＨＲＲＰ序列同樣存在４個散射中心，其微動規律與仿真結果一致。在電磁計算結果中，ＬＳＣ 與ＳＳＣＥ 之間存在較弱的能量，這與點散射模型不能包含目標的全部能量的結論一致。觀察圖１５結果，在二維成像中分別得到了兩個目標ＳＳＣＥ 的特顯點，由于ＬＳＣ 與ＳＳＣＥ之間的能量與ＬＳＣ的能量相當，ＬＳＣ未能在圖像中顯示。

４結論

本文以一個基準坐標系為基礎，將多個目標的觀測坐標系中的位置轉換到基準坐標系下，從而建立了微動多目標的雙基地雷達窄／寬帶回波模型。回波仿真結果與電磁計算結果基本吻合，窄帶回波得到的微多普勒曲線與理論微多普勒曲線一致，寬帶回波得到的時間-ＨＲＲＰ序列與理論微動距離吻合，二維成像中散射中心的坐標與電磁計算結果一致。所提方法能夠快速生成逼真度較高的多目標微動回波，同時也適用于單基地雷達體制，為后續雙基地雷達空間多目標的特征提取、成像方法研究提供參考。

作者簡介

朱義奇（１９９９—），男，博士研究生，主要研究方向為雙基地雷達目標特征提取。

艾小鋒（１９８３—），男，副研究員，博士研究生導師，博士，主要研究方向為雙基地雷達成像、特征提取。徐志明（１９９５—），男，講師，博士，主要研究方向為雙基地雷達目標特性與特征提取。

趙鋒（１９７８—），男，教授，博士研究生導師，博士，主要研究方向為電子信息系統仿真建模評估。

潘小義（１９８６—），男，副教授，碩士研究生導師，博士，主要研究方向為新體制雷達對抗仿真與應用。