生物質CFB氮氧化物排放建模與優化控制

郭炯楠, 高明明, 呂俊復, 岳光溪

(1.華北電力大學 新能源電力系統國家重點實驗室,北京 102206;2.清華大學 能源與動力工程系,北京 100084)

循環流化床(Circulating fluidized bed,CFB)燃燒技術因燃料適應性廣的特性[1],無比契合我國生物質資源種類繁多、品質良莠不齊的國情,近年來在生物質發電領域發展迅速[2]。為響應國家綠色環保政策,我國多地鼓勵新建NOx排放質量濃度不高于50 mg/m3的生物質CFB機組[3]。生物質燃料普遍氮含量低,爐外脫硝效率低[4],所以多數生物質CFB鍋爐廠只通過爐內反應來控制NOx排放量,但生物質CFB具有大遲延、大慣性、安全負荷運行范圍狹窄、爐內燃燒狀況復雜、流化不佳等特征,同時NOx排放系統耦合性強,而我國對生物質鍋爐NOx的控制尚處于試點和起步階段,控制技術目前還不完全成熟。因此,建立動態運行下的生物質CFB NOx排放模型及降低NOx排放系統的耦合性,可以為NOx排放自動控制提供指導,并進一步降低污染物控制成本。

目前,針對生物質CFB大氣污染物排放模型,研究者大多采用數值分析方法,建立相應的靜態數學模型,用于機組設計與改造。同時,我國的生物質資源以秸稈等農業生產副產物為主,而國外長期以木質生物質及其成型燃料為主,因此國外的成熟經驗和技術在我國并不能完全套用,發展出適合我國國情的生物質CFB NOx排放預測模型及控制技術尤為重要[5]。孫俊威等[6]研究了不同生物質氣化氣對爐內燃燒、煙溫及NO生成的影響。Miao等[7]研究發現NOx排放異相反應集中在密相區,而均相反應集中在稀相區。李剛[8]建立了CFB生物質氣化過程模型,用于預測燃料氮元素的遷移特性。張敏[9]在管式爐實驗臺和固定床實驗臺上,通過數值模擬建立了生物質層燃及NOx模型。Trinh等[10]對生物質鍋爐的NOx排放行為進行了深入的三維數值模擬,發現實現NOx排放預測需要考慮碳氮比等因素。Ma等[11]提出了一個綜合計算流體動力學(CFD)模型,該模型建模過程中綜合考慮了NOx化學反應與流動、燃燒模擬。Liu等[12]簡化了CFB生物質立管流體動力學模型,驗證了揮發分氮由NH3和HCN組成的合理性。以上研究可以為機組動態運行污染物排放控制提供機理基礎,但上述模型在成果驗證部分均為實驗室條件下的排放數據,不適用于電廠實際控制策略設計。高昕玥等[13]分析了傳統脫硝技術以及新型脫硝技術的發展現狀和各自優缺點。毛洪鈞等[5]總結了目前國內外NOx燃燒控制技術的優缺點,以及我國目前在生物質鍋爐NOx控制技術方面遇到的瓶頸。因此,根據現實條件設計NOx控制策略,提高NOx排放控制質量具有重要意義。

筆者基于即燃碳模型及氧量模型,應用某130 t/h生物質CFB鍋爐的運行數據,經過機理分析及模型簡化,搭建可適用于實際工程的生物質CFB的 NOx排放模型,對NOx排放質量濃度進行精準預測。基于該模型進行開環階躍試驗,研究給料量和二次風量對NOx排放及氧量動態特性的影響。在此基礎上,針對NOx排放系統耦合強的特征進行解耦設計,提高NOx排放控制質量,為機組實際運行提供指導。

1 生物質CFB NOx排放建模機理

燃料型NOx是生物質燃料中含氮物質在爐內燃燒時經歷一系列復雜反應后生成的污染物,是生物質CFB的主要生成類型,約占燃料燃燒產生NOx質量分數的80%～90%[14]。生物質氮含量大致在1%,生物質燃料NOx生成分為多個階段,第一階段是揮發分氮析出,主要含氮產物為NH3和HCN,NH3與HCN的質量比由生物質燃料種類決定;第二階段是焦油熱裂解和燃燒,產生HCN、NH3和HNCO,考慮到HNCO含量相對較少,且是通過生成HCN來對NOx排放產生影響,因此忽略HNCO的生成;第三階段是即燃碳氮被氧化轉化為NOx[15]。在生物質CFB鍋爐燃燒過程中由于燃料顆粒較大,鍋爐爐膛燃燒的發熱量中,當前時刻的給料量僅占其中的極少部分,而大量存儲在爐膛中燃料的燃燒發熱量為當前鍋爐主導發熱量,將當前大量存儲在爐膛中燃燒的物質稱為即燃碳。燃料氮轉化途徑如圖1所示[16]。

圖1 燃料氮的轉化途徑Fig.1 Conversion pathway of fuel nitrogen

圖2 NOx排放模型邏輯圖Fig.2 Logic diagram of NOx emission model

燃料氮生成NOx后,NOx在爐內發生自還原反應,建立CFB爐內自還原模型,需同時考慮2種還原反應。其一是NO均相還原,本文所用生物質CFB爐膛溫度在1 000 K左右,在此溫度下,占據爐內氣體份額最多的CO幾乎不還原NO,均相還原NO的主要成分為H2、烴類物質以及NH3[17]。其二是即燃碳與NO之間的氣固異相反應,生物質CFB是中低溫燃燒,燃燒反應速率較低,因此爐內存在的大量即燃碳不僅提供了自還原反應吸附表面,還與NO發生了異相還原反應[9]。

2 生物質CFB NOx排放質量濃度模型

筆者以即燃碳模型與氧量模型為基礎,建立爐內NOx自生成模型及自還原模型,自生成模型分為揮發分氮生成與即燃碳氮生成兩部分,自還原模型包括氣體均相還原和即燃碳還原兩部分,前者減后者即為NOx排放質量濃度。揮發分氮析出模型涉及到密相區氧含量,氣體均相還原NOx模型涉及到稀相區氧含量,計算煙氣氧含量需要知道即燃碳的燃燒速率,各個模型互輔互承,共同構成NOx排放質量濃度預測模型。

2.1 氧量模型

從生物質燃料燃燒過程中NOx的生成機理可知,無論是揮發分氮還是即燃碳氮,只有在氧存在的條件下才能被氧化,氧量變化對NOx排放量的影響較為顯著,較低的氧量變化即可有效控制NOx排放量,但氧量的高低同時還會影響鍋爐的燃燒效率和鍋爐排煙熱損失,所以建立準確的氧量機理預測模型具有重要意義。

燃料在空氣中正常燃燒速率為B/tB(其中B為燃料剩余量,tB為固體燃料燃燒時間),但是燃燒劇烈程度與氧含量息息相關,氧含量越高燃燒越劇烈,氧含量越低燃燒越平緩,用密相區氧含量與一次風入爐時氧含量的比值來表示燃料燃燒的劇烈程度。給料遵循質量守恒定律,燃料剩余量B[18]可表示為

(1)

式中:wh為揮發分質量分數,%;qm,c為給料質量流量,kg/s;φom為密相區氧體積分數,%;FO1為一次風氧含量,%;t為時間,s。

密相區氧體積分數考慮一次風帶入帶出氧量以及床料消耗氧量,建立如下模型:

(2)

式中:Vm為密相區容積,m3;F1為一次風風速,m3/h;ηB為固體燃料耗氧系數。

稀相區氧體積分數考慮一次風帶入氧量、一二次風帶出氧量以及燃料揮發分消耗氧量,建立如下模型:

(3)

式中:φox為稀相區氧體積分數,%;Vx為稀相區容積,m3;F2為二次風風速,m3/h;FO2為二次風氧含量,%;ηh為揮發分耗氧系數。

本文所用氧量測點在過熱器下方,考慮一二次風以及給料量等因素,煙氣氧體積分數[19]可表示為

(4)

式中:Vc為爐膛出口到過熱器下方區域容積,m3;φo為煙氣氧體積分數,%;ηxf為旋風分離器分離效率,%;ηhr為揮發分燃燒份額,%;φohin為揮發分帶入氧體積分數,%;φohr為揮發分燃燒消耗氧體積分數,%;T0為273.15 K;γm為氣體摩爾體積,L/mol;Ty為排煙溫度,K;rsc為即燃碳顆粒燃燒速率,kg/s;ηscr為即燃碳的燃燒份額,%。

一次風吹入的燃料可分為4部分:首先是燃燒放熱,其次還有一部分積蓄到床料中,經上面兩步還沒有燃盡的,當作損失存在于飛灰和底渣中。對這四步建立如下模型[20]

(5)

式中:Bsc為即燃碳量,kg;wc為生物質燃料收到基碳質量分數,%;qm,ZF為排放灰渣飛灰質量流量,kg/s;wcZF為排放灰渣飛灰含碳質量分數,%。

即燃碳顆粒燃燒速率為

(6)

式中:M(C)為碳的摩爾質量,g/mol;ksc為即燃碳顆粒燃燒速率常數;cO2m為密相區氧氣濃度,kmol/m3;dc為即燃碳顆粒直徑,m;ρc為即燃碳顆粒密度,kg/m3。

在氧量數據處理過程中,考慮爐膛下部溫度,得到密相區氧氣摩爾濃度如下:

(7)

式中:Tm為密相區溫度。

2.2 NOx自生成模型

NOx的自生成過程復雜,本文做如下簡化:燃料氮分為揮發分氮和即燃碳氮,且兩者的轉化率相同;揮發分氮分為HCN和NH3兩部分;最終排放的NOx均為NO,且進入爐膛立即被轉換;自生成過程全部在密相區進行。

簡化后的模型包括NO、HCN、NH3、O2、H2和H2O 5種成分。假設HCN被氧化的反應為一級反應,其生成NO的反應速率[10]可表示為

(8)

式中:rHCN-NO為HCN氧化生成NO的反應速率,kmol/(m3·s);kHCN-NO為HCN氧化生成NO的反應動力學參數常數;EHCN-NO為HCN氧化生成NO的反應活化能,kJ/kmol;R為氣體常數,8.319 kJ/(mol·K);cHCN為HCN的濃度,kmol/m3。

考慮給料量、揮發分份額、床溫、一二次風量、爐內氧體積分數、積蓄的即燃碳等因素,爐內HCN的摩爾濃度可表示為

(9)

式中:V為爐膛容積,m3;wh_N為生物質揮發分氮質量分數,%;wh_N(HCN)為揮發分氮中HCN質量分數,%;M(HCN)為HCN的摩爾質量,g/mol;F為總風速率,m3/h;M(N)為N的摩爾質量,g/mol;M(NO)為NO的摩爾質量,g/mol;rNO-CxHy為CxHy還原NO的反應速率,kmol/(m3·s);RN為燃料氮轉化率,%。

RN與燃料揮發分相關,其經驗式[21]為

(10)

即燃碳氮取決于燃料結構,據此引入1個參數μ(即燃碳氮與生物質燃料收到基氮的關系系數)。生物質揮發分氮質量分數wh_N[10]可表示為

(11)

式中:wN為生物質燃料收到基氮質量分數,%。

假設NH3被氧化的反應為一級反應,其生成NO的反應速率可表示為

(12)

式中:rNH3-NO為NH3氧化生成NO的反應速率,kmol/(m3·s);kNH3-NO為NH3氧化生成NO的反應動力學參數常數;αT0為密相區溫度指數常數;ENH3-NO為NH3氧化生成NO的反應活化能,kJ/kmol;cNH3為NH3的濃度,kmol/m3;cH2為氫氣的濃度,kmol/m3。

同樣考慮給料量、一二次風量等因素,建立爐內NH3摩爾濃度模型,可表示為

(13)

式中:wh_N(NH3)為揮發分氮中NH3質量分數,%;M(NH3)為NH3的摩爾質量,g/mol;rNO-NH3為NH3還原NO的反應速率,kmol/(m3·s)。

生物質燃料在揮發分析出后,剩余在即燃碳中的即燃碳氮會隨著燃燒氧化為NO,其反應速率[9]可表示為

(14)

式中:rsc_N為即燃碳氮氧化生成NO的反應速率,kg/s;ksc_N為即燃碳氮氧化生成NO的反應動力學常數,與密相區溫度有關,%;wsc_N為即燃碳氮質量分數,%;wsc_C為燃料剩余碳質量分數,%。

即燃碳氮質量分數表達式為

(15)

爐膛內NO自生成速率表達式為

rNOs=M(NO)Vm(rHCN-NO+rNH3-NO)+rsc_N

(16)

式中:rNOs為NO自生成速率,kg/s。

2.3 NOx自還原模型

NOx的自還原過程復雜,本文做如下簡化:自還原分為均相還原與異相還原,均相還原只考慮還原氣體的主要成分H2、烴類物質以及NH3;均相還原在稀相區進行,異相還原在密相區進行。

生物質CFB爐內復雜反應過程中,假定同時產生CO和CO2,二者關系平衡式為

(17)

考慮床溫、粒徑、風量、爐內氧體積分數、即燃碳等因素,CO的濃度可表示為

(18)

式中:cCO為CO濃度,kmol/m3;φ為化學反應的機械因子,與床溫和即燃碳顆粒直徑強相關;M(CO)為CO的摩爾質量,g/mol;kCO2為CO氧化速率常數;cO2x為稀相區氧氣摩爾濃度。

cO2x可表示為

(19)

式中:Tx為稀相區溫度,K。

H2還原NO的反應速率rNO-H2表達式為

(20)

式中:rNO-H2為H2還原NO的反應速率,kmol/(m3·s);kNO-H2為H2還原NO的反應動力學參數常數;ENO-H2為H2還原NO的反應活化能,kJ/kmol;cNOx為稀相區NO濃度,kmol/m3。

有研究表明,在生物質燃燒產生的熱解氣中,H2濃度與CO濃度存在一定的比例關系[14]:

cH2=kH2cCO

(21)

式中:kH2為H2濃度與CO濃度關系系數,%。

NH3還原NO的反應速率rNO-NH3表達式為

(22)

式中:kNO-NH3為NH3還原NO的反應動力學參數常數;ENO-NH3為NH3還原NO的反應活化能,kJ/kmol。

烴類物質對NO的還原作用主要通過中間組分HCN來實現[17],其反應速率可表示為

(23)

式中:kNO-CxHy為CxHy還原NO的反應動力學參數常數;ENO-CxHy為CxHy還原NO的反應活化能,kJ/kmol。

NO被即燃碳還原的異相反應速率可表示為

(24)

式中:rNO-sc為即燃碳異相還原NO的速率,kmol/s;kNO-sc為即燃碳異相還原NO的反應動力學參數常數;ENO-sc為即燃碳異相還原NO的反應活化能,kJ/kmol;S為即燃碳反應面積,m2;cNOm為密相區NO濃度,kmol/m3。

爐膛內NO自還原速率rNOy表達式為

(25)

2.4 NOx排放質量濃度

根據上述3個模型,NOx的自生成量減去自還原量,即為NOx的排放質量濃度,其表達式為

(26)

式中:ρNO為NO排放質量濃度,kg/m3;k1為NOx自還原反應折算系數。

此外,建立NO密相區濃度模型,可表示為

(27)

NO稀相區濃度模型表達式為

(28)

3 仿真驗證

3.1 研究對象

本鍋爐額定蒸汽溫度為540 ℃,額定蒸汽壓力為9.8 MPa,為單鍋筒橫置式,單爐膛,自然循環,全懸吊結構,全鋼架π型布置。鍋爐采用緊身封閉布置,主要由爐膛、絕熱旋風分離器、自平衡回料閥和尾部對流煙道組成。鍋爐燃料元素分析結果見表1。

表1 燃料元素分析Tab.1 Ultimate analysis of fuel

3.2 煙氣氧體積分數模型驗證

NOx排放預測模型是建立在生物質CFB燃燒及流動模型上的,通過驗證其煙氣氧體積分數來檢測模型的準確性。

圖3和圖4分別給出了工況a和工況b煙氣氧體積分數計算值和實測值的對比。如圖3所示,工況a為機組運行13 350 s的數據,機組運行負荷均值為26.32 MW,負荷波動最大速率為2.61%/min,負荷波動最大范圍為5.99 MW。如圖4所示,工況b為機組運行10 800 s的數據,機組運行負荷均值為16.12 MW,負荷波動最大速率為5.01%/min,負荷波動最大范圍為5.09 MW。排煙氧體積分數計算值與實測值的誤差見表2,工況a平均絕對誤差為0.68%、均方差為1.51%、均方根誤差為0.85%;工況b平均絕對誤差為0.52%、均方差為0.94%、均方根誤差為0.62%。工況a和工況b的誤差均在機組實際運行的接受范圍內。

表2 排煙氧體積分數計算值與實測值數據分析Tab.2 Data analysis of calculated and measured values of oxygen content in exhaust gas

圖3 工況a煙氣氧體積分數驗證Fig.3 Verification for oxygen content in the flue gas under condition a

圖4 工況b煙氣氧體積分數驗證Fig.4 Verification for oxygen content in the flue gas under condition b

3.3 NOx排放質量濃度驗證

為驗證脫硝模型的準確性,分別取該機組工況a和工況b運行數小時的運行數據,代入模型進行驗證。

圖5和圖6分別給出了工況a和工況b NOx排放質量濃度計算值和實測值的對比。如圖5所示,工況a取機組運行15 180 s的數據,機組運行負荷均值為26.19 MW,負荷波動最大速率為2.61%/min,負荷波動最大范圍為5.99 MW。工況a模型預測時間約為2 min,如表3所示,平均絕對誤差為2.77 mg/m3、均方差為2.82 mg/m3、均方根誤差為3.52 mg/m3。生物質CFB機組長期接近滿負荷運行,當負荷降低時,鍋爐燃燒不穩定,床溫無法維穩,鍋爐換熱管道的壽命縮短,爐膛溫度低,鍋爐效率下降;當負荷更高時,鍋爐諸多熱損失加劇,鍋爐經濟性能下降。因此,研究安全穩定負荷運行時的各項基本參數特征具有重要意義。

表3 NOx排放質量濃度計算值與實測值數據分析Tab.3 Calculated and measured data analysis of NOx emission concentration

圖5 工況a NOx排放質量濃度驗證Fig.5 Verification for NOx emission mass concentration under condition a

圖6 工況b NOx排放質量濃度驗證Fig.6 Verification for NOx emission mass concentration under condition b

如圖6所示,工況b為機組運行11 040 s的數據,機組運行負荷均值為16.02 MW,負荷波動最大速率為5.01%/min,負荷波動最大范圍為5.09 MW。工況b模型預測時間約為2 min,如表3所示,平均絕對誤差為1.59 mg/m3、均方差為1.26 mg/m3、均方根誤差為1.75 mg/m3。50%運行負荷是生物質CFB機組運行的一種特殊工況,給料、送風不穩定,爐溫降低,排煙溫度降低,不利于機組NOx長期穩定排放,實驗室條件下建立的理論模型在此負荷下適用性較差,本文模型大大提升了其適用性,符合實際工程中的需求。

3.4 開環階躍試驗

以該生物質CFB機組工況a運行參數為研究對象,在3 000 s時分別對給料量和二次風量進行階躍擾動試驗,捕捉NOx排放質量濃度及氧體積分數的動態特性。

如圖7～圖9所示,給料量增加5%時,NOx排放質量濃度先快速上升,然后逐漸下降,最后穩定在比初始值高的平衡點;而氧體積分數則快速下降,最后穩定在比初始值低的平衡點。當給入燃料時,燃料中的揮發分快速析出,NOx排放質量濃度就會立即上升,由于給料量增加,爐內耗氧量增加,氧體積分數減少,爐內還原氣氛增強,但NOx生成量仍然高于還原量,因此當NOx排放質量濃度稍稍下降后,便平衡在高于初始值的位置。

圖7 3 000 s時給料量階躍Fig.7 Step of the feed rate at 3 000 s

圖8 給料量階躍時NOx排放質量濃度的變化Fig.8 Change of NOx emission mass concentration during the step of the feed rate

圖9 給料量階躍時氧體積分數的變化Fig.9 Change of oxygen volume fraction during the step of the feed rate

如圖10～圖12所示,二次風量增加5%時,NOx排放質量濃度先快速下降,然后逐漸上升,最后穩定在比初始值高的平衡點;而氧體積分數則快速上升,最后穩定在比初始值高的平衡點。當送入二次風時,會瞬間吹出爐內部分NOx,同時稀釋爐內NOx質量濃度,并帶入大量氧氣,氧量增加,增強了爐內的氧化氛圍,抑制NOx的還原作用,因此NOx排放質量濃度會先快速下降,但最終排放質量濃度平衡在高于初始值的位置。

圖10 3 000 s時二次風階躍Fig.10 Step of the secondary air flow at 3 000 s

圖11 二次風階躍時NOx質量濃度變化Fig.11 Change of NOx emission mass concentration during the step of the secondary air flow

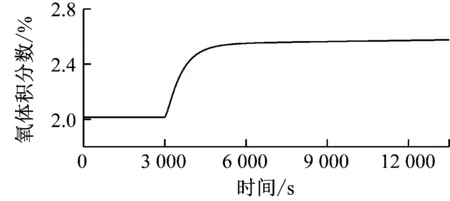
圖12 二次風階躍時氧體積分數的變化Fig.12 Change of oxygen volume fraction during the step of the secondary air flow

4 NOx排放耦合分析與解耦設計

4.1 階躍函數模型辨識

根據上面所確定的NOx排放機理模型,針對所選定的研究對象,對給料量和二次風量做階躍響應試驗,分別得到NOx排放質量濃度與煙氣氧體積分數的實際變化。然后使用Matlab中的系統辨識工具箱(默認辨識方法為最小二乘法)辨識出擬合曲線與傳遞函數模型。

最小二乘擬合法:假定有一組數據xi和yi,i=1,2,…,N,并且己知此數據滿足數學模型y=f(b,x),b為待定系數。最小二乘擬合法的目的即求解出待定系數,使如下目標函數J的值達到最小:

(29)

系統辨識工具箱采用3極點1零點模式的傳遞函數模型,階躍函數辨識結果如表4所示,給料量擾動下NOx質量濃度的階躍函數辨識精度為91.95%,氧體積分數的階躍函數辨識精度為99.75%。二次風量擾動條件下NOx質量濃度的階躍函數辨識精度為96.64%,氧體積分數的階躍函數辨識精度為99.82%。辨識效果如圖13～圖16所示。

表4 階躍函數辨識結果Tab.4 Identification results of step function

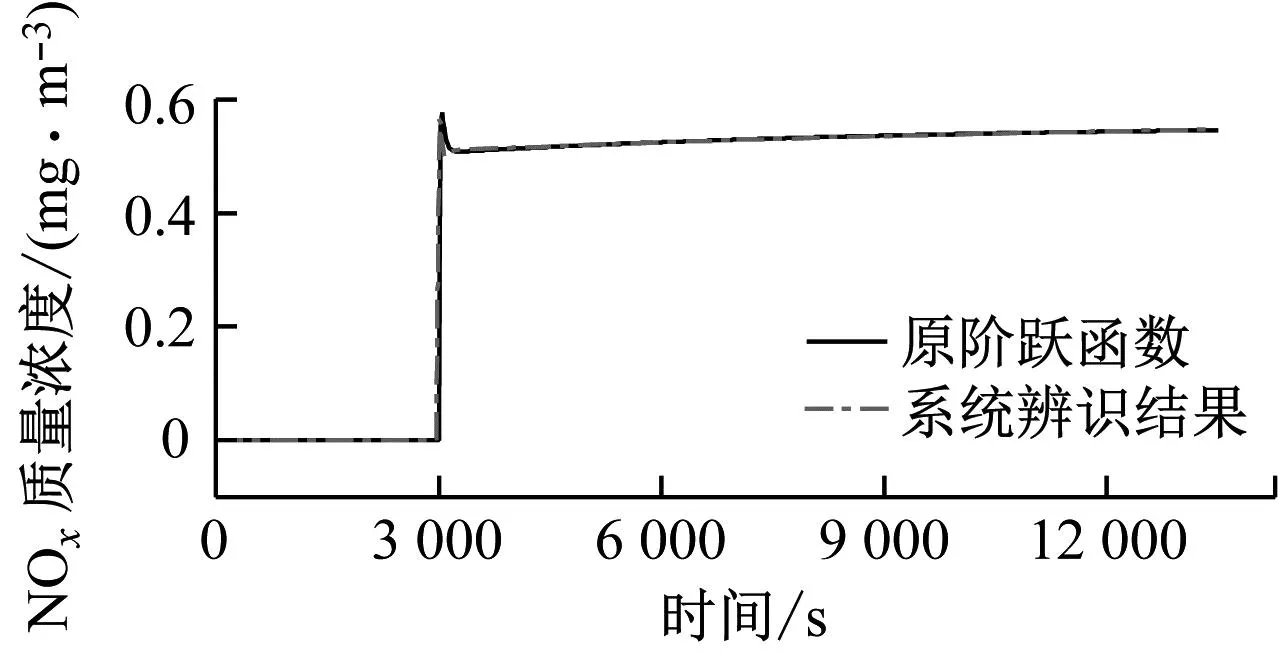
圖13 給料量階躍時NOx排放質量濃度階躍函數辨識效果Fig.13 Identification effect of NOx emission mass concentration step function during the step of the feed rate

圖14 二次風階躍時NOx排放質量濃度階躍函數辨識效果Fig.14 Identification effect of NOx emission mass concentration step function during the step of the secondary air flow

圖15 給料量階躍時氧體積分數階躍函數辨識效果Fig.15 Identification effect of oxygen volume fraction step function during the step of the feed rate

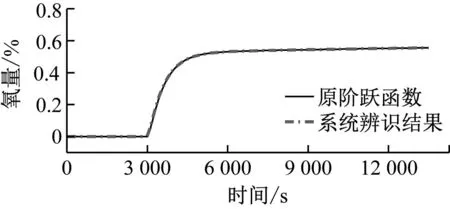
圖16 二次風階躍時氧體積分數階躍函數辨識效果Fig.16 Identification effect of oxygen volume fraction step function during the step of the secondary air flow

4.2 NOx排放耦合分析

NOx排放系統是多輸入多輸出的復雜系統,NOx排放質量濃度與氧體積分數耦合度的大小可用相對增益進行表述[22],相對增益矩陣Λ為

(30)

若矩陣內元素λij∈(0,1),則表明通道ui-yj間存在耦合作用,其中ui為輸入變量,yi為輸出變量,當元素λij趨近于1時,通道的耦合性小,而當元素λij趨近于0時,通道的耦合性就越小,元素趨近于0時,通道匹配有誤,應該對輸入與輸出變量進行重配;λij∈(1,+∞),據相對增益的每一行與列的和等于1的性質,得知一行或列內一定存在元素小于0,這是系統間存在正反饋,此通道變量配對不合理,須再次進行選擇;當一行(列)內的元素相近或者相等時,通道間的耦合作用強,需要對相關系統進行解耦;當對角線上元素為1時通道間沒有耦合作用[23]。

對NOx排放系統來說,NOx排放質量濃度與氧體積分數的耦合狀況能夠通過計算得出。將其耦合關系按矩陣形式表示為

(31)

聯系相對增益公式,將上述傳遞函數的增益代入矩陣,得

(32)

由式(32)可知,NOx排放質量濃度與氧體積分數間存在嚴重耦合,須對它們解耦,否則耦合性強的特性會使系統的整體控制性能降低,包括其響應速度、控制精確度及魯棒性都會受到影響而有所降低。

4.3 NOx排放解耦設計

CFB NOx排放系統中NOx排放質量濃度與氧體積分數的耦合性強,相互干擾,控制效果不理想。因此,引用解耦算法,將多輸入多輸出控制系統轉化成單輸入單輸出的形式,進而提升系統的控制性能。在各類復雜的工業控制過程中,耦合現象是很常見的也是一般會存在的問題。現階段,解耦部分通常使用的設計方案主要包括簡化對角解耦設計和前饋補償解耦設計等。

簡化對角解耦設計、前饋補償解耦設計分別如圖17和圖18所示,其中解耦補償器部分為

圖17 簡化對角解耦控制系統Fig.17 Simplified diagonal decoupling control system

圖18 前饋補償解耦控制系統Fig.18 Feedforward compensation decoupling control system

D12(s)=-G12(s)/G22(s)

(33)

D21(s)=-G21(s)/G11(s)

(34)

4.4 NOx排放解耦控制仿真試驗

分別對給料量、二次風量進行階躍擾動,經簡化對角解耦后NOx排放質量濃度與氧體積分數的響應曲線與未經解耦響應曲線的對比見圖19～圖22。

圖19 給料量擾動下NOx質量濃度響應簡化對角解耦對比Fig.19 Comparison of the responses of NOx mass concentration under disturbance of the feed rate before and after simplified diagonal decoupling

圖19和圖20分別為給料量擾動和二次風量擾動下NOx質量濃度的響應曲線,圖21和圖22分別為給料量擾動和二次風量擾動下氧體積分數的響應曲線,圖中實線為解耦前響應曲線,虛線為解耦后響應曲線。由圖19～圖22可知,給料量擾動時,解耦后氧體積分數的變化相對于解耦前可以忽略不計;而當二次風量擾動時,解耦后的NOx質量濃度變化量相對于解耦前無限趨近于0,即消除了給料量對氧體積分數、二次風量對NOx質量濃度的影響。但是不希望產生變化的變量在該解耦法的作用下也產生了一定的變化。

圖20 二次風擾動下NOx質量濃度響應簡化對角解耦對比Fig.20 Comparison of the responses of NOx mass concentration under disturbance of the secondary air flow before and after simplified diagonal decoupling

圖21 給料量擾動下氧體積分數響應簡化對角解耦對比Fig.21 Comparison of the responses of oxygen volume fraction under disturbance of the feed rate before and after simplified diagonal decoupling

圖22 二次風擾動下氧體積分數響應簡化對角解耦對比Fig.22 Comparison of the responses of oxygen volume fraction under disturbance of the secondary air flow before and after simplified diagonal decoupling

分別對給料量、二次風量進行階躍擾動時,經前饋補償解耦控制后NOx排放質量濃度與氧體積分數的響應曲線與未經解耦的響應曲線的對比見圖23～圖26。

圖23 給料量擾動下NOx質量濃度響應前饋補償解耦對比Fig.23 Comparison of the responses of NOx mass concentration under disturbance of the feed rate before and after feedforward compensation decoupling

圖23和圖24分別為給料量擾動和二次風量擾動下NOx質量濃度的響應曲線,圖25和圖26分別為給料量擾動和二次風量擾動下氧體積分數的響應曲線,圖中實線為解耦前的響應曲線,虛線為解耦后的響應曲線。由圖23～圖26可以看出,簡化對角解耦及前饋補償解耦控制均能起到較好的解耦效果,當給料量進行擾動時,解耦后氧體積分數的變化相對于解耦前可以忽略不計;而當二次風量進行擾動時,解耦后的NOx質量濃度變化量相對于解耦前無限趨近于0,也可以忽略其影響。但是簡化對角解耦算法會對希望進行控制的被控對象造成相對較大的影響,而前饋補償解耦在希望被控對象的響應曲線上與解耦前的差異非常小,在這一點上前饋補償解耦算法的解耦效果要優于簡化對角解耦算法,故選取前饋解耦算法作為解耦補償器的控制策略。

圖24 二次風擾動下NOx質量濃度響應前饋補償解耦對比Fig.24 Comparison of the responses of NOx mass concentration under disturbance of the secondary air flow before and after Feedforward compensation decoupling

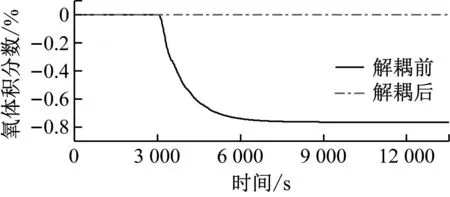
圖25 給料量擾動下氧體積分數響應前饋補償解耦對比Fig.25 Comparison of the responses of oxygen volume fraction under disturbance of the feed rate before and after feedforward compensation decoupling

圖26 二次風擾動下氧體積分數響應前饋補償解耦對比Fig.26 Comparison of the responses of oxygen volume fraction under disturbance of the secondary air flow before and after feedforward compensation decoupling

5 結論

(1) 利用即燃碳模型與氧量模型建立了生物質CFB鍋爐NOx排放質量濃度模型,模型精度可基本滿足130 t/h生物質CFB的工程實際需求。模型計算量較實測量提前2 min,預測效果良好。安全負荷運行下的模型計算值平均絕對誤差為1.23 mg/m3、半負荷運行下的模型計算值平均絕對誤差為0.70 mg/m3。

(2) 對給料量、二次風量進行開環階躍響應試驗,得到NOx排放質量濃度及氧體積分數階躍響應曲線。給料量上升,NOx排放質量濃度上升,氧體積分數下降;二次風量上升,NOx排放質量濃度先下降后上升,氧體積分數上升。階躍響應試驗結果為NOx排放質量濃度控制優化提供了方向。

(3) 對NOx排放質量濃度與氧體積分數的耦合關聯度進行了分析,并采用當前常用的簡化對角解耦法與前饋補償解耦法對兩系統進行解耦,仿真結果證明前饋補償解耦法能夠行之有效地解除NOx排放質量濃度與氧體積分數間的強耦合性,實現單輸入單輸出的回路控制,對實現快速、精準的控制提供了基礎。

(4) 本文所建立的模型具有較高精度,階躍試驗得到NOx排放質量濃度及氧體積分數的動態特性,可為生物質CFB動態運行過程中的NOx控制提供運行指導,對強耦合性的NOx排放系統進行解耦設計,取得了較好的解耦結果,后續將以此模型及其解耦控制為基礎,建立相應的自動控制策略。