一種波段聚類和多尺度結構特征融合的高光譜圖像分類模型
王彩玲,張 靜,王洪偉,宋曉楠,紀 童
1. 西安石油大學計算機學院,陜西 西安 710065 2. 西北工業(yè)大學光電與智能研究院,陜西 西安 710072 3. 甘肅農業(yè)大學草業(yè)學院,甘肅 蘭州 730070
引 言
高光譜遙感技術利用光譜探測與成像技術對感興趣物體成像,形成了高光譜圖像立方體。 它包含豐富的光譜和空間信息,是一個三維數(shù)據(jù)[1],因此被廣泛應用于生態(tài)保護[2]、 災害監(jiān)測[3]、 醫(yī)療衛(wèi)生[4]等領域。 在高光譜(hyperspectral image,HSI)數(shù)據(jù)處理任務中,分類仍然是一項具有挑戰(zhàn)性的任務,旨在為每個像元分配唯一標簽,對許多實際應用非常關鍵。 一開始,我們通過人眼進行分類,取得了不太理想的效果。 到后來,利用機器學習方法雖然提高了分類精度,但仍存在許多問題: (1)樣本稀少引發(fā)的“Hughes”現(xiàn)象; (2)高冗余信息以及噪聲問題; (3)“同物異譜”和“同譜異物”現(xiàn)象。 這些問題導致分類精度較低,不利于后續(xù)的圖像分析。
為了克服這些問題,多種特征提取方法用于保持光譜分辨能力。 一些基于特征變換的方法如主成分分析[5],獨立主成分分析,它們在降低光譜維度的同時保留了數(shù)據(jù)的原有信息,但卻改變了波段本身的物理意義。 另外一種基于波段選擇的方法由于保留了高光譜數(shù)據(jù)的固有屬性而備受關注。 它在不損失物理意義和信息的前提下,選擇了低相關性,信息量大的子集。 波段相似性度量方式包括: 信息散度(information divergence,ID)、 歐氏距離(Euclidean distance,ED)[6]等。
研究表明,僅提取數(shù)據(jù)內部的光譜信息對高光譜分類并不充分。 近年來,利用HSI光譜和圖像信息的光譜-空間分類方法已被廣泛研究。 例如,為了得到圖像內部的紋理特征,1973年,Haralick等引入了灰度共生矩陣(gray level co-ccurennce matrix,GLCM)的概念,通過計算像元之間的聯(lián)合概率密度得到灰度關系。 2019年,Tan等提出了三維GLCM光譜-空間分類方法,該模型利用GLCM特征圖像提取異質性組織內部的紋理特征,取得了不錯的效果[7]。 Ojala等提出了局部二值模式(local binary patterns,LBP),由于對灰度變化敏感度低且計算速度快,也被用于圖像的紋理分析。 再后來,形態(tài)學(morphology profile,MP)、 擴展形態(tài)學[8]、 多屬性輪廓特征[9]等方法被提出,使得分類精度進一步提高。 2015年,Dalla等將獨立主成分分析(independent component analysis,ICA)和擴展形態(tài)學相結合對高光譜遙感影像進行分類,實驗分析證明了此方法在圖像空間信息建模的有效性[10]。 Hou等提出了一種基于三維形態(tài)剖面(3D-MP)的光譜空間分類方法,該模型充分利用了三維光譜空間特征,在樣本有限的情況下提高了分類精度[11]。 近些年,眾多學者開展基于濾波的分類技術研究。 典型的有小波變換、 Gabor濾波[12]等。 Pablo等提出一種基于小波變換和數(shù)學形態(tài)學的光譜空間技術,該方法不僅提取到了數(shù)據(jù)的深層空譜特征,還證明了對圖像噪聲問題的魯棒性[13]。 Jia等提出了基于光譜-空間Gabor表面特征(GSF)融合的空譜分類模型,該方法保留了數(shù)據(jù)內部豐富的光譜-圖像信息,進一步提升了分類性能[14]。 慕彩紅等提出了一種基于空間坐標的光譜-空間特征融合的HSI分類算法,將HSI在空間維度上劃分為若干小圖像,根據(jù)空間坐標特征和光譜特征分別得到各類別樣本的概率,SVM進一步對概率特征進行分類,得到最終的分類結果[15]。 目前,基于空間信息和光譜信息相結合的方法已經成為高光譜圖像分類的主流方法,研究證明,空譜特征聯(lián)合是提高分類性能的有效方法,能降低椒鹽噪聲的影響,取得較好的區(qū)域一致性結果。 然而,現(xiàn)有的光譜空間特征提取方法仍面臨以下幾個挑戰(zhàn):
(1)這些方法引入空間信息的方式更復雜,在一定程度上增加了計算成本。
(2)地物含有復雜的紋理、 結構特征,現(xiàn)有的模型大多只考慮了單一尺度下的光譜特征與空間特征的融合,而沒有考慮多尺度下光譜特征與空間特征的豐富相關性。
(3)現(xiàn)有的特征提取方法大多沒有考慮到由于弱光或其他因素可能產生的圖像噪聲。 在這種不完善的情況下,現(xiàn)有的光譜空間特征提取方法的性能往往會嚴重下降。
為了解決以上這些問題,從數(shù)據(jù)中提取足夠的空譜聯(lián)合特征,提出了一種波段聚類和多尺度結構特征融合的高光譜圖像分類模型,其新穎性和貢獻主要包括以下兩個方面:
(1)考慮到相鄰波段的相關性高于非相鄰波段的相關性,使用基于光譜散度信息的聚類方法將高光譜數(shù)據(jù)分為有限的、 波段數(shù)量不等的子立方體,在每個子立方體中求取平均值疊加后作為光譜特征輸出,從而實現(xiàn)高質量帶圖像的選擇。
(2)圖像的整體結構信息才是人類視覺感知系統(tǒng)的主要感知數(shù)據(jù),而紋理等“細節(jié)特征”往往是不需要的。 在不同的參數(shù)設置下去除圖像的紋理細節(jié)部分,將主結構從復雜的紋理圖像中提取出來,得到多尺度結構特征信息,可以有效的去除噪聲,增加不同類別之間的差異。
實驗結果表明,該模型不僅充分提取了高光譜數(shù)據(jù)內部的空譜特征,還對小樣本問題非常有效。
1 研究方法
1.1 歸一化
為了消除指標間量綱以及奇異樣本數(shù)據(jù)導致的不良影響,需要對數(shù)據(jù)進行歸一化處理,如式(1)所示
(1)
Indian Pines數(shù)據(jù)內部光譜波段差別較大,因此我們對其進行歸一化。 設X為空間中某一像素點,表示為X={x1,x2,…,x200},由于它有200個光譜波段,對其歸一化處理的步驟如式(2)所示
(2)
式(2)中,xmin為X中的最小光譜值,xmax為X中的最大光譜值。Xnew(i)為X歸一化后新的像素值。
University of Pavia數(shù)據(jù)內部空間物質相似而像素值差別很大,因此對空間維進行歸一化,該數(shù)據(jù)空間維大小為610×340,將其拉伸為一維向量,可以表示為Y={y1,y2,…,y207 400},對其歸一化處理的步驟如式(3)所示
(3)
式(3)中,ymin為Y中的最小光譜值,ymax為Y中的最大光譜值。Ynew(i)為Y歸一化后新的像素值。
1.2 光譜特征提取框架-自適應子空間劃分策略
在高光譜數(shù)據(jù)中,波段之間的相似性與其距離相關。 設原始高光譜圖像立方體為L,I為光譜波段總數(shù)。 為了快速對高光譜數(shù)據(jù)進行分割,首先,我們采取粗劃分策略,將數(shù)據(jù)L均分為n個波段數(shù)為Z的子空間,如式(4)和式(5)。
(4)
L→{l1,l2,…,ln}
(5)
其中,li(i≤n)為粗劃分后的子空間。 為了對每個粗子空間li進行更加準確的表示,我們采取細劃分策略來獲取新的子空間。 由于相距遠的波段相關性極小,因此我們僅考慮相鄰子空間li,li+1(i+1≤n)內的波段。 具體過程如下: (1)將每個空間波段拉伸為一維向量; (2)用信息散度構造相鄰波段的相似性矩陣; (3)對相鄰子空間按照最大化類間距離與類內距離比值的方法進行自適應劃分。 細劃分策略后目標函數(shù)的形式如式(6)所示
argmin(dintra-dinter)
(6)
式(6)中,dinter是相鄰兩個子空間的類間距離,定義如式(7)所示
dinter=max|dID(m,n)|
(7)
式(7)中,dID(m,n)表示第i(i≤n)個子空間中的波段m和第i+1個子空間中的波段之間的信息散度值。
dintra是子空間類內距離,定義如式(8)—式(10)所示
dintra=Mi+Mi+1
(8)
(9)
(10)
式中,dID(p,q)為同一個子空間內第p和第q個波段之間的信息散度值。Mi和Mi+1表示相鄰子空間散度和的平均值,t為第i個子立方體中包含的頻帶總數(shù)。 通過粗細劃分策略后,子空間表示如式(11)。
B={b1,b2,b3,…,bn}
(11)
由于自適應劃分后的子空間內包含不同數(shù)目的波段,我們對每個子空間內的光譜波段求取平均值,具體如式(12)所示
Avgb={avgb1,avgb2,avgb3,…,avgbn}
(12)
式(12)中,Avgb表示每個子空間光譜平均值avgbi疊加后的結果。 圖1為自適應子空間劃分的光譜特征提取框架。
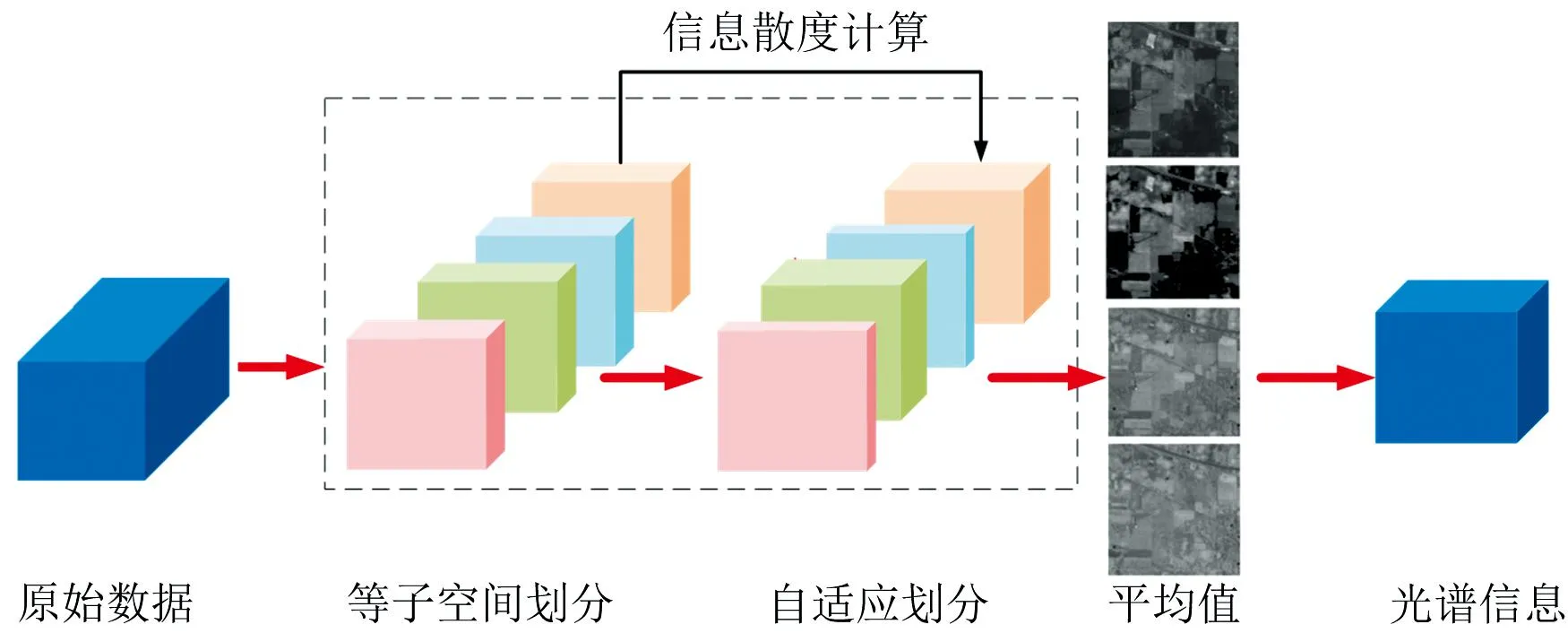
圖1 自適應子空間劃分策略-光譜特征提取框架Fig.1 Adaptive subspace partitioning strategy-spectral feature extraction framework
1.3 空間特征提取框架-多尺度相對全變分
為了從高光譜圖像數(shù)據(jù)中獲取有用的空間特征,結構特征提取扮演著越來越重要的角色。 相對全變分(relative total variation,RTV)方法作為其中的一種,可以有效地減小類內差異,增大類間差異,并且對于椒鹽噪聲和紋理特征的去除也至關重要。 然而,由于參數(shù)σ和λ直接影響著RTV的效果,因此,單一尺度下的結構特征無法滿足高光譜數(shù)據(jù)結構豐富,物質多樣的特性。
針對RTV的缺點,通過設置多參數(shù),對光譜特征數(shù)據(jù)進行不同尺度下的相對全變分提取,形成多尺度相對全變分(multi-scale RTV,MRTV)空間特征提取框架,如式(13)和式(14)所示。
fi=RTV(I,λi,σi) (i≤c)
(13)
F={f1,f2,f3,…,fc}
(14)
式中,I為原始高光譜數(shù)據(jù),假設I的波段數(shù)為m,對I進行c次不同參數(shù)設置下的RTV計算,可以得到c個波段數(shù)為m的特征子集{f1,f2,f3,…,fc}。λi和σi分別表示控制平滑度和空間尺度的參數(shù)。fi為第i個特征子集,波段數(shù)為m。F表示c個特征子集按光譜維堆疊后的立方體數(shù)據(jù),波段數(shù)為m×c。
雖然MRTV有效地提取了高光譜數(shù)據(jù)內部的結構特征,但由于堆疊操作導致了高維性,增加了計算成本。 由于核主成分分析(kernel PCA,KPCA)對于提高像素的光譜可分離性和降低光譜維度非常有效,因此在數(shù)據(jù)堆疊之后進行KPCA處理,具體過程如式(15),N為P中保留的主成分數(shù)量,P為最終特征輸出。 特征提取過程如圖2所示。
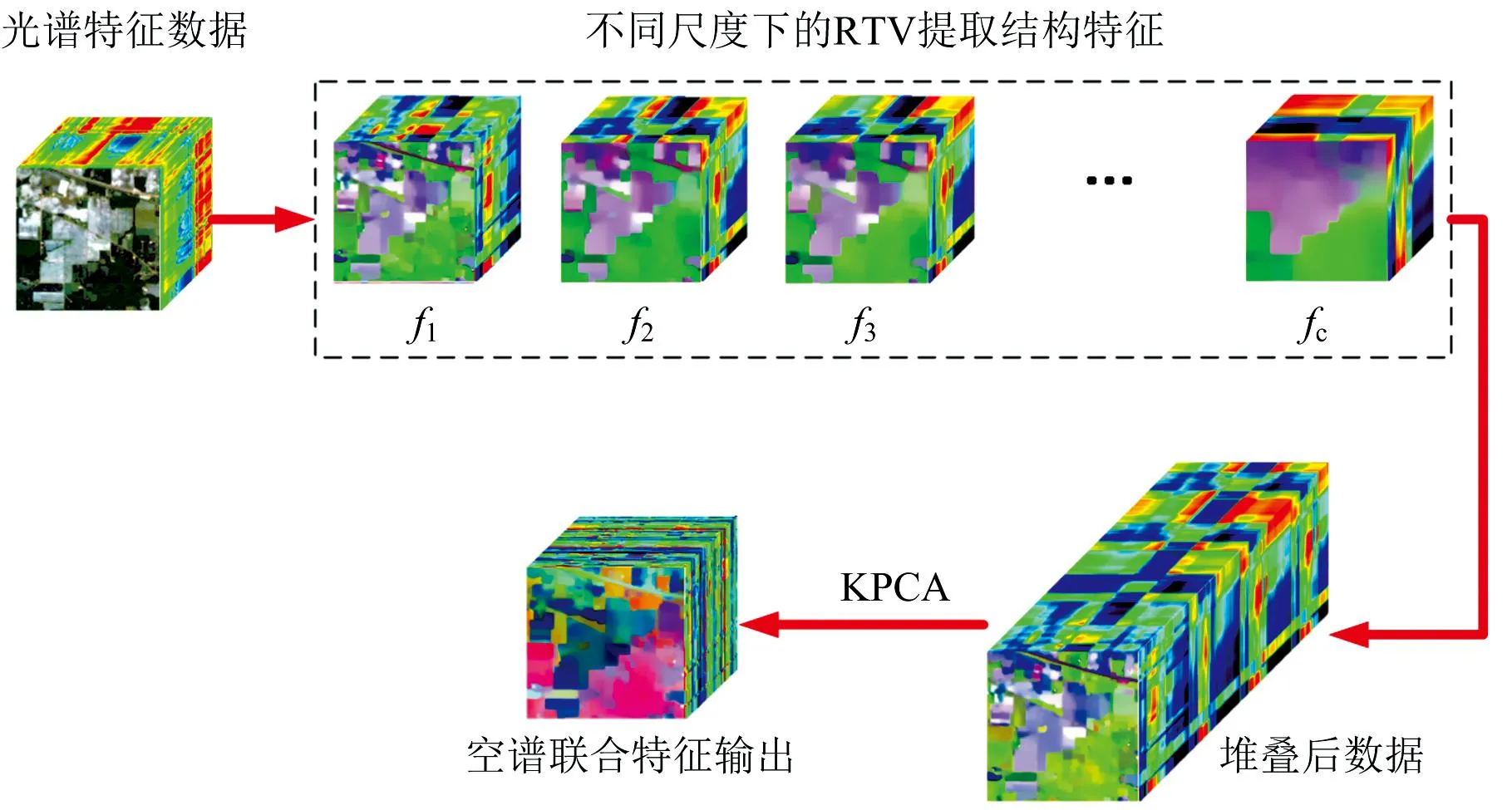
圖2 空間特征提取框架-多尺度相對全變分Fig.2 Spatial feature extraction framework-multi-scale relative total variation
P=KPCA(F,N)
(15)
1.4 空譜特征提取框架-波段聚類和多尺度結構特征融合
提出了一種波段聚類和多尺度結構特征融合的高光譜圖像分類模型(ASPS-MRTV),為了充分提取高光譜數(shù)據(jù)內部的光譜特征和空間特征,分別構建了自適應子空間劃分策略(adaptive subspace partitioning strategy,ASPS)光譜特征提取框架和多尺度相對全變分空間特征提取框架。 過程如下:
(1) 對高光譜數(shù)據(jù)進行歸一化處理;
(2) 根據(jù)式(4),將原始高光譜數(shù)據(jù)L均分為n個波段數(shù)為Z的子空間;
(3) 將每個空間波段拉伸為一維向量后用ID構造相鄰波段的相似性矩陣;
(4) 根據(jù)式(7)—式(10)對細劃分策略后的目標函數(shù)式(6)進行求解;
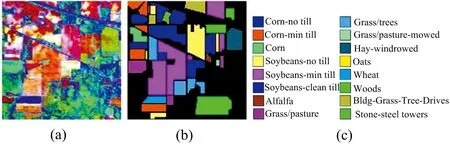
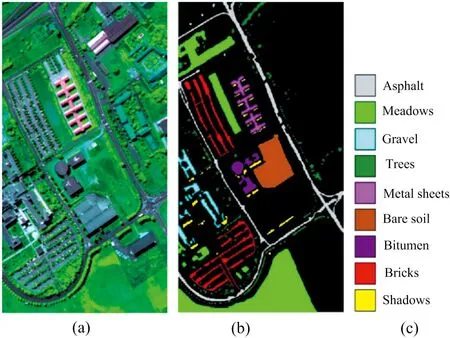
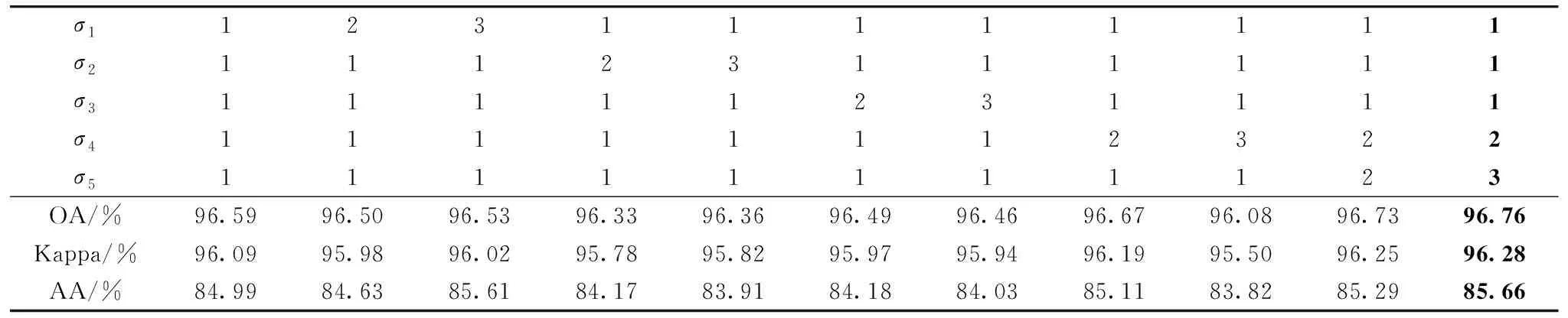
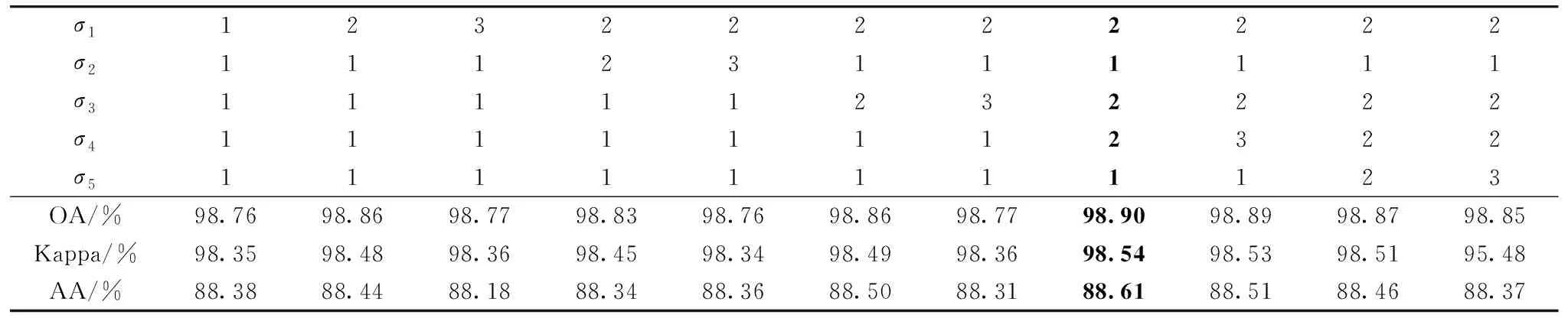
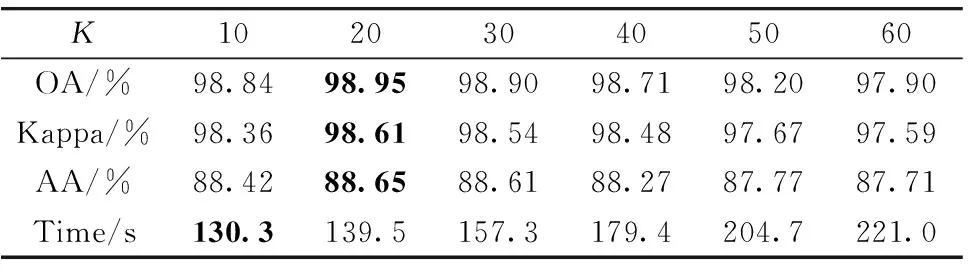
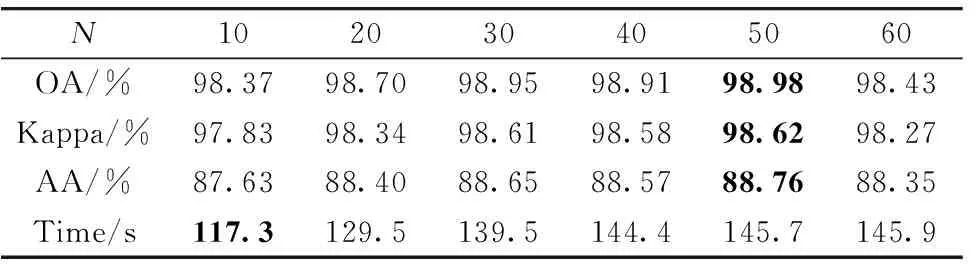
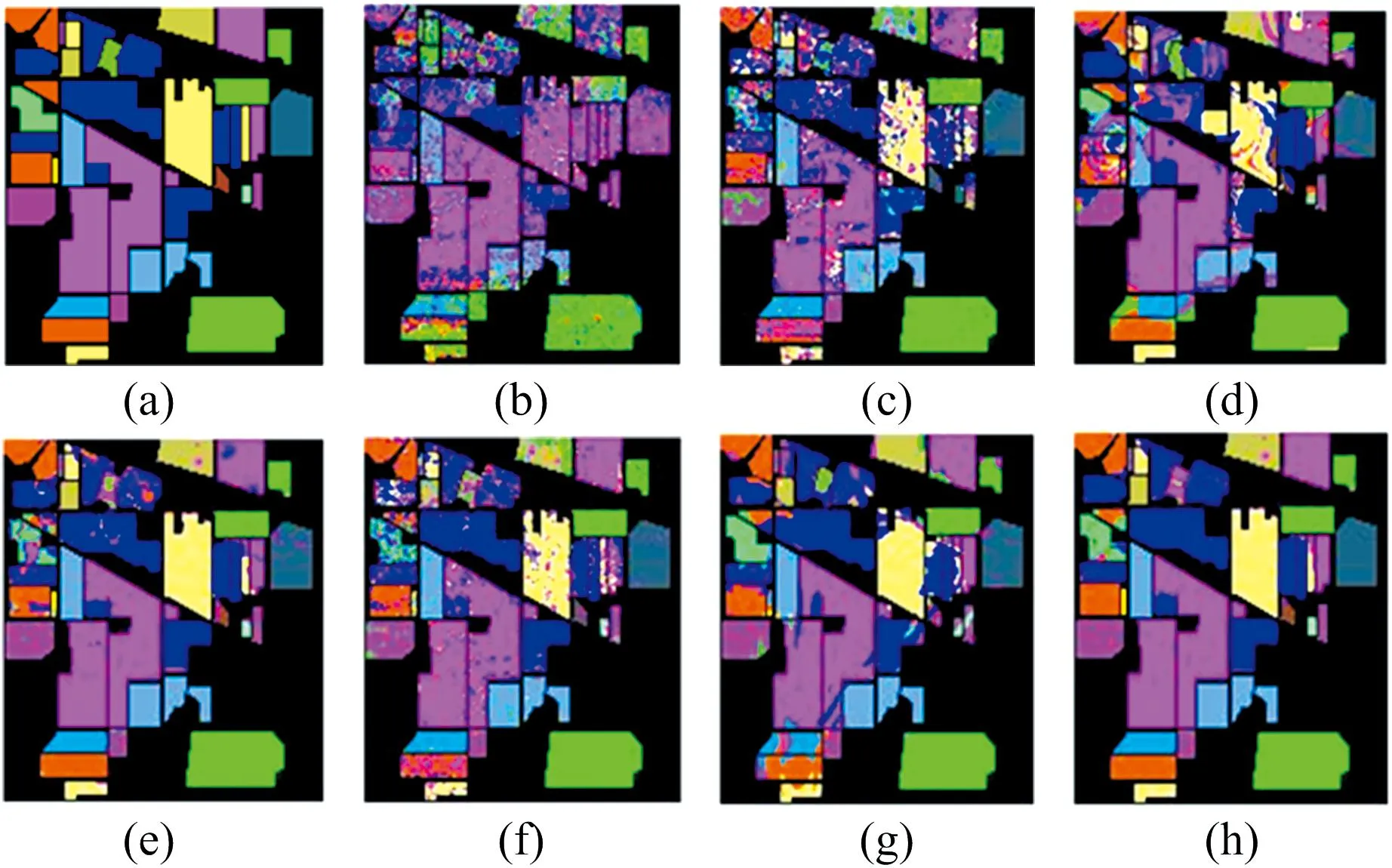
(5) 通過粗細劃分策略后得到自適應子空間bi(i (6) 對每個子空間bi求取光譜波段平均值得到avgbi; (7) 將每個自適應子空間內的平均值avgbi進行疊加,得到Avgb; (8) 利用MRTV空間特征提取框架對Avgb進行多尺度特征提取,將得到的多個子空間按光譜維堆疊形成立方體數(shù)據(jù)F; (9) 對立方體數(shù)據(jù)F進行KPCA處理后得到空譜特征P。 流程圖如圖3所示。 圖3 空譜特征提取框架-波段聚類和多尺度結構特征融合Fig.3 Frame-band clustering and multi-scale structural feature fusion for spatial spectrum feature extraction Indian Pines數(shù)據(jù)(簡稱為IP)由紅外成像光譜儀在印第安拍攝所獲取的。 數(shù)據(jù)大小為145×145×220,具有20 m的空間分辨率,光譜范圍為0.2~0.4 μm。 實驗中去除20個水吸收區(qū)域的光譜帶,保留了200個波段。 圖4為IP數(shù)據(jù)的偽彩圖,地面真值圖及標簽。 圖4 Indian Pines數(shù)據(jù)(a): 偽彩圖; (b): 地面真值圖; (c): 標簽Fig.4 Indian Pines data(a): False color map; (b): Ground truth map; (c): Label University of Pavia數(shù)據(jù)(簡稱為UP)是由ROSIS-3在帕威亞大學拍攝所獲取的。 數(shù)據(jù)大小為610×340×115,實驗中去除12個水吸收區(qū)域的光譜帶,保留了103個波段,空間分辨率為1.3 m,光譜覆蓋范圍為0.43~0.86 μm。 圖5為UP數(shù)據(jù)的偽彩圖,地面真值圖及標簽。 圖5 University of Pavia數(shù)據(jù)(a): 偽彩圖; (b): 地面真值圖; (c): 標簽Fig.5 University of Pavia data(a): False color map; (b): Ground truth map; (c): Label 實驗環(huán)境為Windows10和Matlab2019a,處理器為Inter Core I7-8750,GPU為NVIDIA GeForce GTX1050Ti,內存為16 GB。 實驗過程中,訓練樣本為5%的IP數(shù)據(jù)以及1%的UP數(shù)據(jù),測試樣本為剩余的樣本。 為了驗證波段聚類和多尺度結構特征融合框架(ASPS-MRTV)的有效性,我們使用懲罰參數(shù)C和核參數(shù)σ都為24.5的SVM進行分類,并采用OA、 AA和 Kappa 系數(shù)來評價分類效果的好壞。 實驗中各參數(shù)及其含義如表1所示。 表1 各參數(shù)及其含義Table 1 Parameters and their meanings 結構特征質量的好壞是由RTV的參數(shù)λ和σ決定的。 通常情況下,將λ固定在[0,0.05]之間,σ固定在[1,3]之間。 為了避免高光譜數(shù)據(jù)結構特征的單一性,考慮到時間復雜度和空間復雜度的影響,設置了包含大小尺度的5個λ,λ1=0.003,λ2=0.015,λ3=0.01,λ4=0.02,λ5=0.05,實驗過程中,采用控制變量的方法對σ調優(yōu),設置K=N=30,σ1-σ5為1,σ在IP上的尋優(yōu)的結果如表2所示,最優(yōu)精度加粗表示。 表2 σ在IP上的調優(yōu)過程Table 2 Process of optimizing σ for IP 參數(shù)K的優(yōu)化也至關重要。 一開始,將K設置為30,由于IP數(shù)據(jù)包含200個光譜波段,所以將K固定在[10,100]之間,實驗結果如表3所示。 同樣地,也將N固定在[10,100]之間,具體結果見表4,最優(yōu)結果加粗表示。 表3 參數(shù)K對IP的分類效果Table 3 IP classification effect of parameter K 表4 參數(shù)N對IP的分類效果Table 4 IP classification effect of parameter N 從表2的實驗結果可知,當σ1=1,σ2=1,σ3=1,σ4=2,σ5=3時IP數(shù)據(jù)的分類效果最好,此時OA=96.76%,Kappa=96.28%,AA=85.66%。 由表3可以得知,當K=30時,OA,Kappa,AA都取得了最高的分類精度,分別達到了96.76%,96.28%,85.66%。 另外我們也發(fā)現(xiàn),當參數(shù)K不斷增大時,OA呈現(xiàn)出先增大后減小的趨勢。 這是由于當K較小時包含的有用信息也少,但隨著K的不斷增大,有用信息變多,分類精度也就提高了,然而當K過大時信息的冗余又導致分類精度下降,所以才會出現(xiàn)先增大后減小的現(xiàn)象。 由表4可知,當N=20時,OA,Kappa都達到了最高,分別為97.06%,96.64%。 隨著N的增大,分類精度也呈現(xiàn)出先增大后減小的趨勢。 實驗過程中以OA的好壞為第一標準。 對于IP數(shù)據(jù),考慮到訓練時間的影響,綜合各指標,設置λ1=0.003,λ2=0.015,λ3=0.01,λ4=0.02,λ5=0.05,σ1=1,σ2=1,σ3=1,σ4=2,σ5=3,K=30,N=20。 對于UP數(shù)據(jù),σ調優(yōu)過程的實驗結果如表5所示。 由于UP數(shù)據(jù)包含103個光譜波段,所以將K和N分別固定在[10,60],具體結果見表6與表7。 最優(yōu)結果加粗表示。 表5 σ在UP上的調優(yōu)過程Table 5 Optimization process for σ on UP 表6 參數(shù)K對UP的分類效果Table 6 UP classification effect of parameter K 表7 參數(shù)N對UP的分類效果Table 7 UP classification effect of parameter N 由表5可知,當σ1=2,σ2=1,σ3=2,σ4=2,σ5=1時,UP數(shù)據(jù)的分類精度最高,OA達到98.90%,Kappa達到98.54%,AA達到88.61%。 同樣的,對于UP數(shù)據(jù),也研究了參數(shù)K和N對分類結果的影響。 從表6可以看出,隨著K增大,OA,AA和Kappa大體上呈現(xiàn)出先增大后減小的趨勢,當K=20時,各項指標最高,此時OA=98.95%,Kappa=98.61%,AA=88.65%。 由表7可知,當N=50時,分類精度最高,OA達到98.98%,Kappa達到98.62%,AA達到88.76%,除此之外,OA隨著N的增加也呈現(xiàn)出先增大后減小的趨勢。 綜上,對于UP數(shù)據(jù),設置λ1=0.003,λ2=0.015,λ3=0.01,λ4=0.02,λ5=0.05,σ1=2,σ2=1,σ3=2,σ4=2,σ5=1,K=20,N=50。 為了驗證本文提出的波段聚類和多尺度結構特征融合框架(ASPS-MRTV)的效果,分別與SVM、 ASPS(ED)、 ASPS(ID)、 ASPS-LBP、 ASPS-GlCM、 ASPS-BF等方法進行對比。 實驗中統(tǒng)一使用C和σ都為24.5的SVM進行分類。 (1) SVM: 直接使用SVM對高光譜數(shù)據(jù)進行分類; (2) ASPS(ED): 僅使用光譜特征提取框架-自適應子空間劃分策略獲取光譜維度信息,波段相似性度量使用歐式距離; (3) ASPS(ID): 僅使用光譜特征提取框架-自適應子空間劃分策略獲取光譜維度信息,波段相似性度量使用信息散度; (4) ASPS-LBP: 使用光譜特征提取框架-自適應子空間劃分策略獲取光譜維度信息,再利用局部二值模式(LBP)獲取空間信息,設置B=10,R=1; (5) ASPS-GlCM: 使用光譜特征提取框架-自適應子空間劃分策略獲取光譜維度信息,再利用灰度共生矩陣(GLCM)獲取空間信息,選擇4個不同的方向(0°,45°,90°,135°); (6) ASPS-BF: 使用光譜特征提取框架-自適應子空間劃分策略獲取光譜維度信息,再利用雙邊濾波器(BF)獲取圖像的空間信息,設置w=15、δα=8、δr=3; (7) ASPS-MRTV(AM): 使用我們提出的波段聚類和多尺度結構特征融合的方法獲取光譜-空間信息。 首先對IP數(shù)據(jù)使用上述7種方法進行實驗,得到的結果如表8所示。 表8 IP上不同方法的分類精度Table 8 Classification accuracy of different methods on IP 從表8中可以看出,與其他方法相比,我們提出的波段聚類和多尺度結構特征融合的空譜特征提取框架有著最高的分類性能,OA=97.06%,Kappa=96.64%,AA=85.95%。 由分類結果可知,SVM的分類精度高于ASPS(ED),驗證了歐式距離(ED)雖然對計算波段間相似性有效,但對高維空間并不適合。 與ASPS(ED)方法相比,ASPS(ID)的OA提高了28.44%,驗證了信息散度不僅對波段信息相似度有效,也可以在降低高光譜圖像立方體數(shù)據(jù)維度的同時,保留更完整和有用的信息。 與SVM相比,ASPS(ID)的OA提高了9.8%,驗證了光譜特征提取框架-自適應子空間劃分策略對IP數(shù)據(jù)的類別可分性更加有效。 與ASPS-GlCM、 ASPS-LBP相比,ASPS-BF、 ASPS-MRTV的OA有了大幅度的提高,驗證了對于高光譜數(shù)據(jù)而言,結構特征比紋理特征更能提高分類精度,這是由于結構特征提取技術更能去除噪聲,紋理等無用的空間信息。 與ASPS-BF相比,ASPS-MRTV的分類精度提高了5.24%,驗證了空間特征提取框架-多尺度相對全變分(MRTV)更能充分利用高光譜數(shù)據(jù)內部的空間信息,有效減少椒鹽噪聲和紋理特征的影響。 圖6為七種方法對IP數(shù)據(jù)的分類結果圖,可以看出與其他六種方法相比,ASPS-MRTV的錯誤分類標簽最少,與地面真實圖更相近。 圖6 不同特征提取對IP分類圖(a): 地面真實圖; (b): SVM; (c): ASPS(ED); (d): ASPS(ID); (e): ASPS-LBP; (f): ASPS-GlCM; (g): ASPS-BF; (h): AMFig.6 IP classification maps by different feature extraction methods(a): Ground map; (b): SVM; (c): ASPS(ED); (d): ASPS(ID); (e): ASPS-LBP; (f): ASPS-GlCM; (g): ASPS-BF; (h): AM 對于UP數(shù)據(jù),表9給出了不同方法獲得的分類精度。 最優(yōu)結果如表中加粗值所示,可以看到,OA=98.98%,Kappa=98.62%,AA=88.76%。 與SVM相比,其余六種方法都獲得了較高的分類精度,驗證了通過提取高光譜圖像的空間和光譜信息,可以提高圖像特征分類的準確性。 與ASPS(ED)相比,ASPS(ID)的OA提高了0.91%,再次驗證了在細劃分策略中,使用信息散度構造波段間相似矩陣的有效性。 與ASPS(ID)和ASPS(ED)相比,ASPS-LBP、 ASPS-GlCM、 ASPS-BF、 ASPS-MRTV的分類精度更高,這是因為前兩種方法僅考慮了高光譜數(shù)據(jù)內部的光譜特征,忽略了圖像內部相鄰像素之間的空間相關性,導致分類精度較低,也再次說明了空譜特征提取方式對于識別不同地物類別非常有效。 與ASPS-GlCM和ASPS-LBP相比,ASPS-BF和ASPS-MRTV分類效果更好,再次驗證了對于高光譜圖像立方體而言,充分利用數(shù)據(jù)內部的結構特征對分類精度提升更有效。 表9 UP不同方法的分類精度Table 9 Classification accuracies of different methods for UP 圖7為七種方法對UP數(shù)據(jù)的分類效果圖。 可以看出,SVM與僅使用光譜特征提取的ASPS(ID),ASPS(ED)存在更多的錯誤分類標簽,相比之下,ASPS-BF和ASPS-MRTV分類誤點較少,證明了結構特征對嚴重噪聲問題的魯棒性。 提出了一種波段聚類和多尺度結構特征融合的高光譜圖像分類模型(ASPS-MRTV)。 一方面,為了充分提取圖像內部的光譜信息,構造了基于自適應子空間劃分策略的特征提取框架,首先通過粗劃分對原始數(shù)據(jù)進行等分,之后通過細劃分策略對等子空間進行自適應,最后將每個自適應子空間的平均值進行疊加形成光譜特征。 另一方面,構造了多尺度相對全變分方法,用于提取高光譜圖像的結構特征,通過設置多參數(shù),對粗細劃分策略后的光譜數(shù)據(jù)進行不同尺度下的RTV提取,達到了信息互補的效果,最后使用KPCA對堆疊數(shù)據(jù)進行處理,得到高光譜圖像立方體的空譜特征。 與其余六種方法相比較,ASPS-MRTV獲得了更高的精度,但也存在一些不足,比如運行時間過長,在后續(xù)的研究中,將進一步優(yōu)化模型的時間復雜度,以提取更具判別力的空譜特征。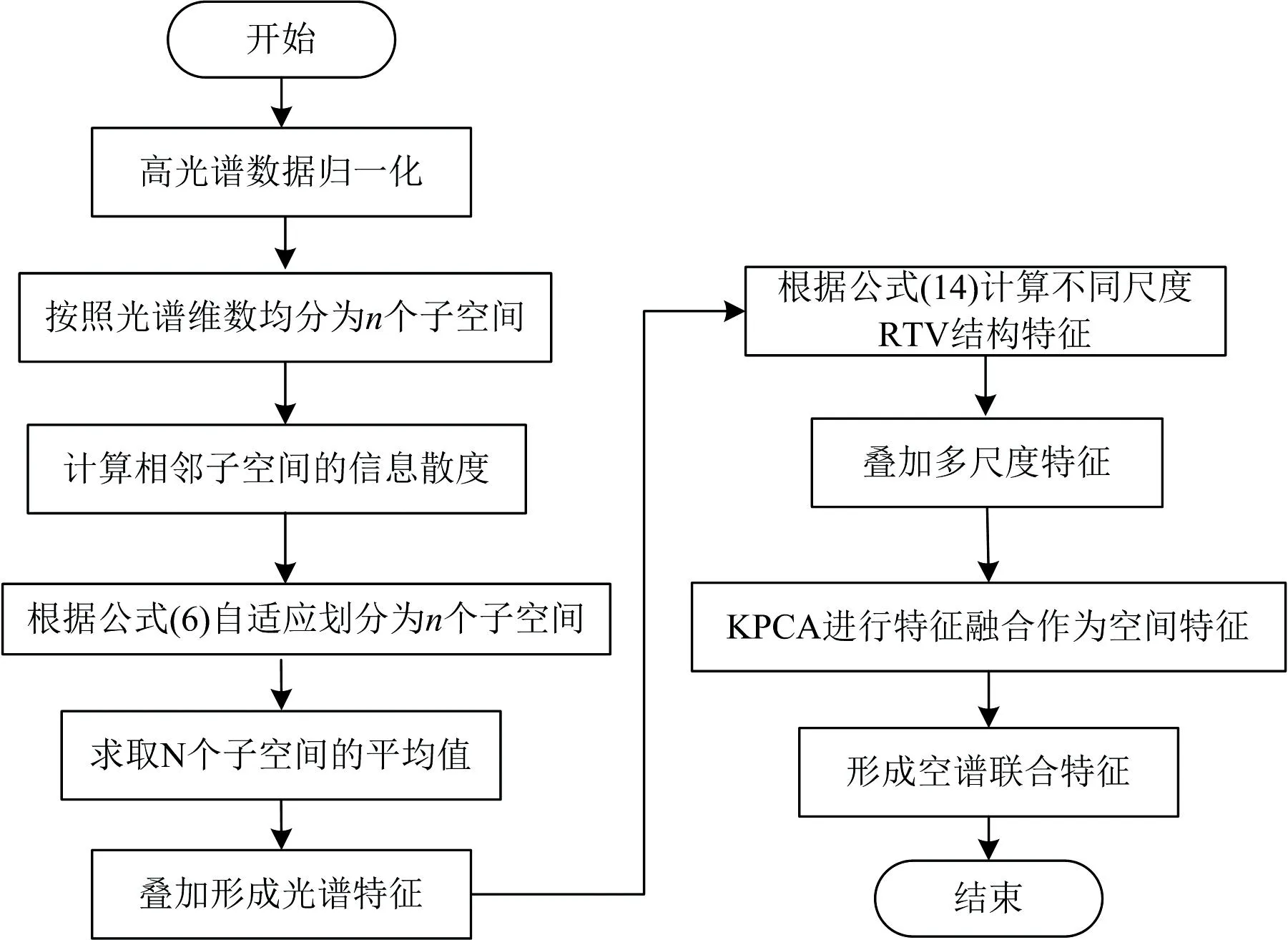
2 實驗部分
2.1 數(shù)據(jù)集
2.2 實驗設置
2.3 參數(shù)優(yōu)化


2.4 結果對比


3 結 論

