淺析高中數學中函數的構造問題
魏明亮
(東莞市東莞中學松山湖學校,廣東 東莞 523000)
函數中的構造問題往往是學生很難掌握的內容之一.這類題具有結構獨特、技巧性高、綜合性強等特點,我們需要熟悉常見的幾種函數的構造模型,如果構造合理,將有助于學生快速解題.下面我們將對構造函數的規律方法進行歸類總結并舉例說明[1].
1 利用f(x)與x構造
例1已知函數f(x)在R上滿足f(x)=f(-x),且當x∈(-∞,0]時,f(x)+xf′(x)<0成立,若a=20.6f(20.6),b=ln2f(ln2),c=-3f(-3),則a,b,c的大小關系是什么?
解析已知函數f(x)在R上滿足f(x)=f(-x),所以f(x)是偶函數.
構造函數g(x)=xf(x),則g′(x)=f(x)+xf′(x).
由題意可知,當x∈(-∞,0]時,有f(x)+xf′(x)<0成立,即g′(x)<0恒成立,所以g(x)=xf(x)在(-∞,0]上單調遞減.
又因為g(x)=xf(x)為奇函數,
所以g(x)在R上單調遞減.
因為-3 所以g(-3)>g(ln2)>g(20.6). 即a 因為當x>0時,有xf′(x)-f(x)>0, 所以有h′(x)>0. 因為1<2 即a 推廣1若出現nf(x)+xf′(x)形式,則構造函數g(x)=xnf(x)[2]. 例3已知定義在R上的函數f(x)滿足f(x)+f′(x)>0,且有f(3)=3,則f(x)>3e3-x的解集為____. 解析構造函數g(x)=exf(x),又因為f(x)>3e3-x,所以f(x)·ex>3e3.即g(x)>g(3). 因為f(x)+f′(x)>0在R上恒成立,所以g′(x)=ex[f(x)+f′(x)]>0在R上恒成立. 所以g(x)=exf(x)在R上單調遞增. 又因為g(x)>g(3),所以x>3. 所以f(x)>3e3-x的解集為{x|x>3}. 例4已知可導函數f(x)的導函數為f′(x),若對任意的x∈R,都有f′(x) Af(2) C.e2f(-1)>f(1) D.e2f(-1) 因為對任意的x∈R,都有f′(x) 所以h′(x)<0恒成立. 又因為-1<0<2,根據單調性可知,h(-1)>h(0)>h(2),所以A,C選項正確. 推廣3若出現nf(x)+f′(x)形式,則構造函數g(x)=enxf(x). 常用構造的形式有以下幾種: (1)g(x)=f(x)sinx,g′(x)=f′(x)sinx+f(x)cosx. (3)g(x)=f(x)cosx,g′(x)=f′(x)cosx-f(x)sinx. 通過觀察可以發現這些導函數中都含有f(x),f′(x),sinx,cosx四個相同的量,因為(sinx)′=cosx,(cosx)′=-sinx,所以在f(x)與sinx的構造中,g′(x)出現的是和的形式,h′(x)出現的是差的形式;而在f(x)與cosx的構造中,g′(x)出現的是差的形式,h′(x)出現的是和的形式. 解析根據題意,構造函數g(x)=f(x)sinx,又因為f(x)為奇函數,有 g(-x)=f(-x)sin(-x)=f(x)sinx=g(x). 所以g(x)=f(x)sinx在R上為偶函數. 所以g′(x)=f′(x)sinx+f(x)cosx. 當x∈(0,+∞)時,有f′(x)sinx+f(x)cosx<0恒成立,即g′(x)<0恒成立. 所以g(x)在(0,+∞)上單調遞減. 所以h(x)也為偶函數. 這類題型往往是將自變量相同的項放一起,再根據題意構造具體的函數. A.sinα>sinβB.cosα>cosβ C.cosα 即sinβ>cosα,所以選項C正確; 所以選項D正確. 例8若2a+log2a=4b+2log4b,則下列選項正確的是( ). A.a>2bB.a<2bC.a>b2D.a 解析根據指數和對數的運算性質可知 4b+2log4b=22b+log2b. 又因為2a+log2a=4b+2log4b, 即有2a+log2a=22b+log2b. 所以構造函數f(x)=2x+log2x(x>0), 所以f(x)在(0,+∞)上單調遞增. 則f(a)=2a+log2a,f(2b)=22b+log22b=22b+log2b+1>22b+log2b=f(a). 即f(2b)>f(a). 因為f(x)在(0,+∞)單調遞增,所以2b>a. 即選項B正確. 指對同構經常使用的變換形式有兩種,一種是將x變成lnex,然后構造函數;另一種是將x變成elnx,然后構造函數. 例9設a,b都為正數,e為自然對數的底數,若aea A.ab>e B.b>eaC.ab 解析因為b=elnb,所以aea aea 因為a,b都為正數,且blnb>aea>0, 所以lnb>0. 所以構造函數f(x)=xex(x>0). 所以f(a) 又因為f′(x)=ex(x+1)>0在(0,+∞)上恒成立,所以f(x)在(0,+∞)上單調遞增. 所以a 所以選項B正確. 數學是一門創造性的藝術,需要極強的數學抽象、邏輯推理能力,巧妙地構造函數在解決數學問題中具有很高的研究和欣賞價值.構造法需要以足夠的知識經驗為基礎,以較強的觀察能力、綜合運用能力為前提,根據題目的結構特征,對問題進行深入分析,找出已知與所求問題的紐帶.雖然構造函數的形式多種多樣,但我們可以從嘗試解題過程中總結規律,分析結構特征,找到構造函數的依據,從而實現構造.
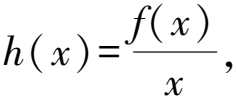

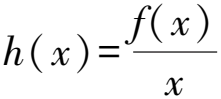
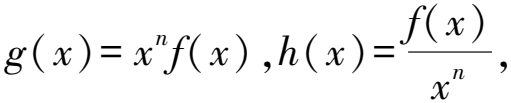
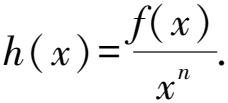
2 利用f(x)與ex構造
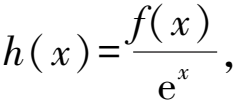
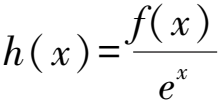
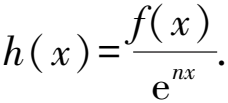
3 利用f(x)與sinx,cosx構造

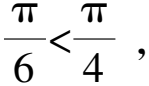

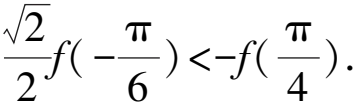

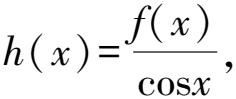




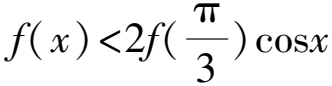

4 構造具體函數關系式




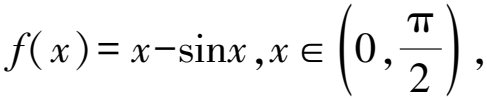







5 同構法構造函數

