深度探究一道拋物線模擬題
李 寒
(貴陽市第一中學,貴州 貴陽 550081)
數學的精髓在于不斷探索和創新.在數學解題教學的實施過程中,應不斷地從中發現新問題,獲取有用的新信息,提出新穎觀點,探求解決問題的新方法,歸納得出新規律,進而適時地將問題延伸推廣為一般性結論用于解決相關聯的問題.唯有這樣,才能逐步培養學生靈活多變的思維品質和探索精神,提升學生的數學核心素養和創新意識,從而真正把能力的培養落到實處.
1 試題呈現
題目(2023屆廣州市一模第6題)已知拋物線C的頂點為坐標原點O,焦點F在x軸上,過點(2,0)的直線交C于P,Q兩點,且OP⊥OQ,線段PQ的中點為M,則直線MF的斜率的最大值為( ).
2 試題解答
分析1 根據題設條件,設出拋物線C與直線PQ的方程,然后利用垂直關系求出拋物線C的方程及點M的坐標,再利用斜率公式建立函數關系,最后應用均值不等式解得最值.
解法1 由題可知,拋物線C的焦點F在x軸的正半軸上,設拋物線C的方程為y2=2px(p>0).
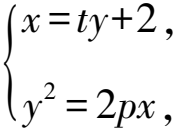
y2-2pty-4p=0.

y1y2=-4p.
由OP⊥OQ,得
解得p=1.

所以點M(t2+2,t).
顯然若直線MF的斜率最大,則必有t>0.

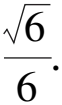
故選A.
分析2 根據單選題的題型特點,利用下面拋物線的“二級結論1”,可迅速秒求p的值.
解法2見結論1證明之后.
3 結論推廣
思考1過拋物線作兩條互相垂直的弦,分別交拋物線于P,Q兩點,則直線PQ具有怎樣的位置關系?經探究,有:
結論1 過拋物線C:y2=2px(p>0)的頂點作兩條互相垂直的弦,分別交拋物線于P,Q兩點,則直線PQ必過定點(2p,0).

化簡整理,得
2px-(y1+y2)y+y1y2=0.
由OP⊥OQ,得
解得y1y2=-4p2.
所以直線PQ的方程為
2px-(y1+y2)y-4p2=0.
令y=0,得x=2p.
所以直線PQ過定點(2p,0).
若直線PQ的斜率不存在,易得P(2p,2p),Q(2p,-2p),所以直線PQ仍過定點(2p,0).從而結論1得證.
根據結論1,我們可以給出試題的解法2了.
解法2由結論1可知2p=2,解得p=1.以下同解法1.
4 逆向探究
思考2 若對結論1進行逆向思考,即將直線過定點作為題設,是否能得到“垂直”關系?經探究,于是有:
結論2 過定點(2p,0)的直線分別交拋物線C:y2=2px(p>0)于P,Q兩點,O為坐標原點,則OP⊥OQ.
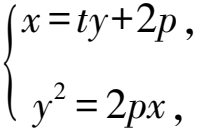



故OP⊥OQ.
5 縱向探究
思考3 結論1中,OP⊥OQ中的點O是拋物線C上的一個特殊的定點(頂點),若把定點O換作拋物線C的其它位置,那么是否能夠得到與結論1同樣的結論?即直線PQ仍過定點呢?
結論3 過拋物線C:y2=2px(p>0)上的定點T(x0,y0)作兩條互相垂直的弦,分別交拋物線于P,Q兩點,則直線PQ必過定點(x0+2p,-y0).

化簡整理,得2px-(y1+y2)y+y1y2=0.
①


因為點T(x0,y0)在拋物線C上,
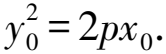
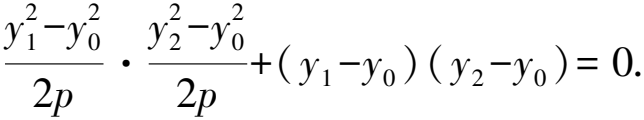
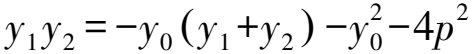
=-y0(y1+y2)-2px0-4p2.
代入①并整理,得
2p(x-x0-2p)-(y1+y2)(y+y0)=0.
可知直線PQ過定點(x0+2p,-y0).
若直線PQ的斜率不存在,即y2=-y1.
則直線PQ的方程為x=2p+x0.
此時顯然直線PQ也過定點(x0+2p,-y0).
思考4 對于結論3中,若延長TP和TQ,則“TP⊥TQ”也可以理解為直線TP與直線TQ的傾斜角之差為90°,那么當直線TP與直線TQ的傾斜角之和為90°時,直線PQ是否也過定點呢?
結論4 過拋物線C:y2=2px(p>0)上的定點T(x0,y0)作傾斜角之和為90°的兩條直線,分別交拋物線C于P,Q兩點,則直線PQ必過定點(x0-2p,-y0).
結論4的證明,可仿照結論3的證明過程進行,這里從略,請讀者自行完成.
思考5 沿著結論4的思路,進一步變換角度思考:當直線TP與直線TQ的傾斜角之和為180°時,直線PQ是否還過定點呢?有沒有其它情形呢?
結論5 已知T(x0,y0)是拋物線C:y2=2px(p>0)上的一個定點,P,Q是拋物線C上使直線TP與直線TQ的傾斜角之和為180°的兩點,則直線PQ的斜率為定值,即線段PQ是一組平行弦.
證明由題意可知直線TP與直線TQ均不垂直于坐標軸,即直線TP的斜率kTP與直線TQ的斜率kTQ均存在且不為0.
因為直線TP與直線TQ的傾斜角之和為180°,所以kTP+kTQ=0,即kTP=-kTQ.

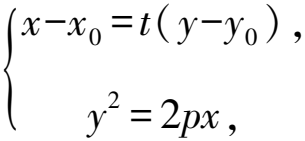
y2-2pty-2pty0-2px0=0.
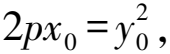
所以y=y0(舍去)或y=2pt-y0.



因此直線PQ的斜率

故線段PQ是一組平行弦.
思考6 在結論5的基礎上,作一般性思考:當直線TP與直線TQ的斜率之積為常數時,直線PQ是否也能夠過定點呢?


化簡整理,得
2px-(y1+y2)y+y1y2=0.
①
由kTP·kTQ=λ,得

因為點T(x0,y0)在拋物線C上,
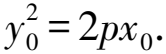



代入①并整理,得

6 類比探究
思考7 橢圓、雙曲線與拋物線有許多類似的結論,能否將拋物線的結論3類比推廣到橢圓和雙曲線呢?經探究,于是有:


結論7與結論8的證明可按結論3的證明過程進行,這里從略,請讀者自行完成.
對典型模擬題的多角度探究,就是指對問題從不同視角來審視,以不同的切入點探究問題,其實質是對試題的“二次開發”.通過對試題的剖析和思考,展開問題的來龍去脈和知識間的縱橫聯系,站在一定的高度去思考問題,突出數學本質,使知識達到融會貫通,使思維得到升華,進而優化數學思維品質[1].

