一道開放性橢圓試題的探究與推廣

欒 功

(南寧市第三中學,廣西 南寧 530021)

《普通高中數學課程標準(2017年版2020年修訂)》在高考命題建議中明確提出:命題時,應包括開放性問題和探究性問題,重點考查學生的思維過程、實踐能力和創新意識[1].這一指導思想在近兩年的各類考試命題中也得以體現,且較多集中在以數列和解三角形等知識為背景的結構不良問題上.而2022年一次西南大聯考中圓錐曲線大題一改往日常態,以開放的探究型問題呈現,不論是試題的知識背景還是問題的呈現形式,都給考生耳目一新的感覺.

1 試題呈現

題目(2022屆“3+3+3”高考備考診斷性聯考)點M是圓A:x2+(y+1)2=16上任意一點,點B(0,1),線段MB的垂直平分線交半徑AM于點P,當點M在圓A上運動時.

(1)求點P的軌跡E的方程;

(2)BQ∥x軸,交軌跡E于點Q(點Q在y軸的右側),直線l:x=my+n與E交于C,D兩點(l不過點Q),且CQ與DQ關于BQ對稱,則直線l具備以下哪個性質?證明你的結論.①直線l恒過定點;②m為定值;③n為定值.

分析試題第(1)問考查了圓的簡單幾何性質與橢圓的定義,體現了試題的基礎性;第(2)問以圓錐曲線共軛弦性質為背景設計了與動直線l有關的開放型問題,給考生創設了自主思考的情境,便于考生多角度、開放地思考問題,試題考查考生獨立地對問題提出見解并進行論證的能力,綜合性強,對學生直觀想象、邏輯推理、數學運算等素養都有較高的要求.

2 解法分析

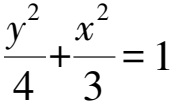
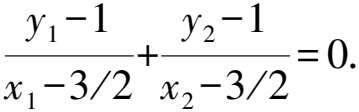
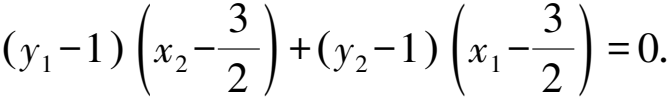
代入x1=my1+n,x2=my2+n,整理,得

(3+4m2)y2+8mny+4n2-12=0.

代入①式,得

整理,得4m2+(4n-8)m-2n+3=0.

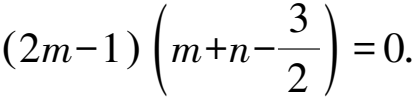
點評解法1從直線l入手構圖設參,通過對“直線CQ與DQ關于BQ對稱”這一幾何關系的坐標刻畫,自然而然聯系到運用韋達定理是解答這類問題的通性通法,其揭露的試題本質特征和內在聯系為進一步探究其他解法、剖析試題本質、培養學生思維的深刻性和創造性等提供了基礎.

(3+cos2α)t2+(6sinα+12cosα)t=0.

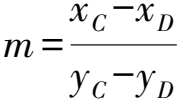
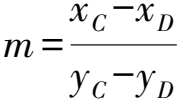
點評該解法從直線QC,QD的傾斜角入手,應用直線的參數方程解題,在幾何關系代數化的過程中緊緊抓住直線QC,QD的邏輯結構的對稱性,利用同構思想和三角恒等變換進行坐標運算,結構整齊、簡潔明了.該解法不僅體現了參數法在解答解析幾何問題中的重要作用,同時還開闊了學生的解題視野.

則變換后的橢圓方程為

整理,得

4x′2+3y′2+12x′+6y′=0.

②

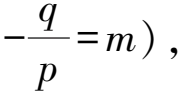
4x′2+3y′2+(12x′+6y′)(px′+qy′)=0.

即(4+12p)x′2+(3+6q)y′2+(6p+12q)x′y′=0.

兩邊同時除以x′2,得

③

由于平移變換后點Q的坐標變為Q′(0,0),

故kQ′C′,kQ′D′是方程③的兩個根.

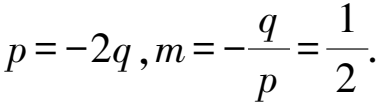
由kQC+kQD=0,得

整理,得

3y1y2+3y1-3y2-4x1x2-6x1+6x2+6=0,

④

3y1y2-3y1+3y2-4x1x2+6x1-6x2+6=0.

⑤

④-⑤,得

6(y1-y2)-12(x1-x2)=0.

點評該解法的靈感源于對教材習題的理解,把橢圓的標準方程改寫為第三定義的形式,在求解這類問題時收獲意想不到的效果,同時彰顯了坐標法的神秘與魅力.

上述四種解法從不同側面闡釋了直線l在運動過程中保持的規律性,即直線QC與QD的斜率之和為定值0時,直線CD的斜率為定值2.這一發現也啟發我們進一步深入思考,如直線CD的斜率為定值是巧合嗎?如果不是,它又與哪些量有必然的聯系?

3 推廣探究

思考1 在試題的解答過程中我們發現當kQC+kQD=0時,直線CD的斜率為定值,這個定值與點Q有關嗎?

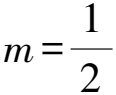
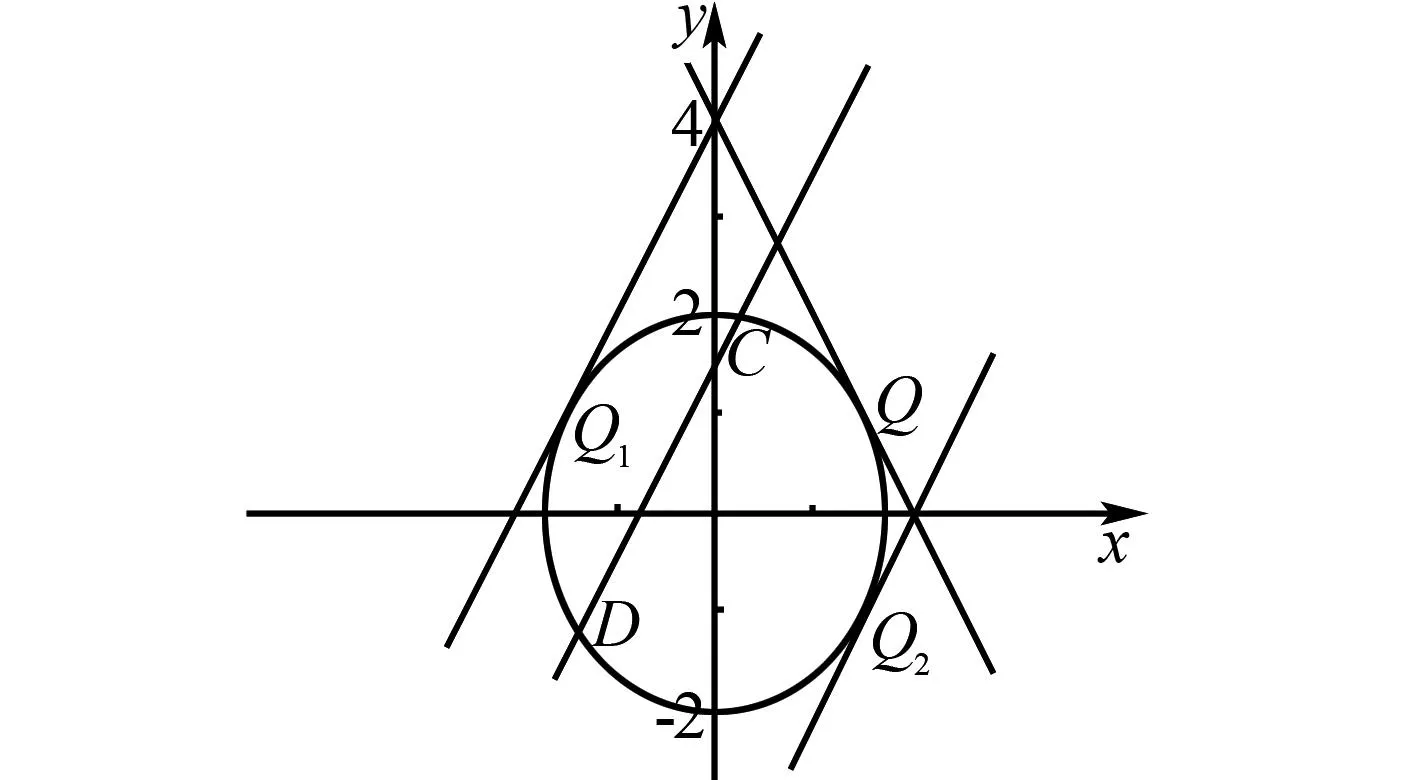
圖1 思考1示意圖

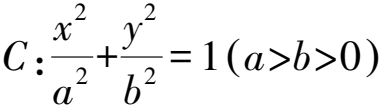
思考2由圓錐曲線定義的統一性猜想,拋物線與雙曲線是否也有類似性質?

變式1點P(x0,y0)(y0>0)為拋物線C:y2=2px(p>0)上一定點,A(x1,y1),B(x2,y2)為拋物線C上兩動點,若直線PA與PB斜率存在且互為相反數時,證明直線AB的斜率是非零常數.

證明因為點P(x0,y0),A(x1,y1),B(x2,y2)在拋物線y2=2px上,所以

⑥

⑦

⑧

⑥-⑦,得

(y0-y1)(y0+y1)=2p(x0-x1).

由kPA+kPB=0,得

即有y1+y2=-2y0.

⑧-⑦,得

(y2-y1)(y2+y1)=2p(x2-x1).

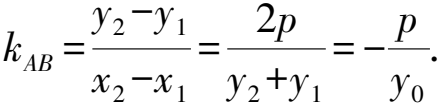
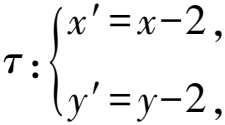
整理,得

4x′2-y′2+16x′-4y′=0.

⑨

設直線l′的方程為px′+qy′=1(其中p=4q),代入⑨式,得

4x′2-y′2+(16x′-4y′)(px′+qy′)=0.

即(4+16p)x′2-(1+4q)y′2+(16q-4p)x′y′=0.

即(4+16p)x′2-(1+4q)y′2=0.

兩邊同時除以x′2,得

⑩

由于平移變換后點Q的坐標變為Q′(0,0),

故kQ′A′,kQ′B′是方程⑩的兩個根.

由于平移變換下不改變直線的斜率,

所以k1+k2=0.

推廣2 設點Q(x0,y0)是對稱軸平行于坐標軸的定圓錐曲線(包括圓、橢圓、雙曲線和拋物線)C上一定點,A,B是C上兩個動點,若直線QA,QB的斜率互為相反數,則直線AB的斜率存在時為定值,等于曲線C在點Q處切線斜率的相反數(當曲線C為雙曲線時,點A,B在同支上).

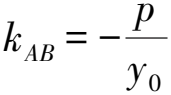
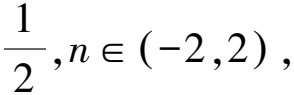
由解法3可知,當kQC+kQD=0時,直線l′:px′+qy′=1中p,q滿足p=-2q,直線l′的方程可寫為q(y′-2x′)-1=0,當y′-2x′=0時,-1≠0,所以直線l′不過定點,從而直線l不過定點.如果我們嘗試改變kQC+kQD的值或運算形式,直線l是否會過定點?

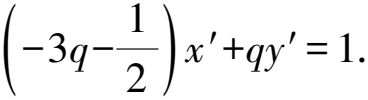
因此直線l′過定點(-12,6).

通過變式探究發現,當直線QC,QD的斜率之和、之積為非零常數時,直線CD恒過定點,同樣也有一般性結論,在此不再一一羅列,感興趣的讀者可以進一步地發散思考與探究,在嘗試提出更高探究性問題的過程中歷練更高層次的思維,形成更深刻的理解和感悟.