變化中找不變 探究中培能力
——2023屆高三元月大聯考理數20題的深入探究

王東海

(安徽省合肥市肥東縣城關中學,安徽 合肥 231600)

在解析幾何的四種圓錐曲線里,其中橢圓與圓是關系緊密的兩個研究對象,它們的圖形有著很強的對稱性.另外橢圓中會生成很多圓,如蒙日圓、伴隨圓、基圓和內切圓等,它們在性質上具有怎樣的關系?再者橢圓中出現的撲朔迷離的變化中蘊含著哪些不變性?本文以一道2023屆高三元月大聯考圓錐曲線試題為例,通過對問題的解法探究、引申拓展、追本溯源,從而建構此類題的處理方法.

1 考題呈現

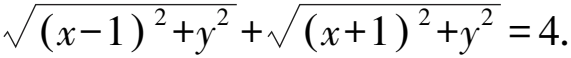
(1)求點P的軌跡方程.

2 解法探究

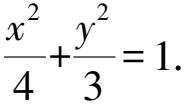
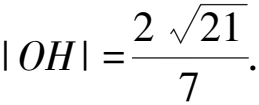
當直線l的斜率存在時,設直線l的方程為y=kx+m,且設A(x1,y1),B(x2,y2),再聯立橢圓方程并消去y可得(3+4k2)x2+8kmx+4m2-12=0[1].

所以△=48(3+4k2-m2)>0,

即m2<3+4k2.

即7m2-12k2-12=0.

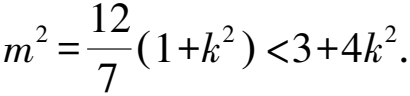
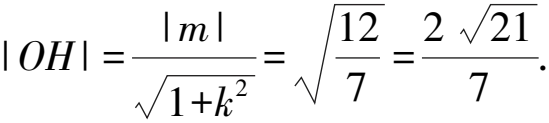
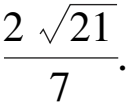
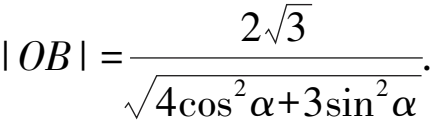
視角2 射線OA,OB過原點,故也可設出OA的方程,通過直曲聯立可得A,B兩點的坐標,最后用三角形等面積法可以求出|OH|的值.

又當直線OA斜率存在時,則設其方程為y=kx.聯立橢圓C的方程并消去y得

(3+4k2)x2-12=0.

①

②

視角3 觀察題目所給條件,有斜率之積為-1的條件,故可考慮使用齊次化法加以處理.

解析3 因直線AB不過原點,故設直線l的方程為mx+ny=1,且設A(x1,y1),B(x2,y2),

對已知橢圓方程3x2+4y2-12=0配湊得

3x2+4y2-12(mx+ny)2=0.

即(3-12m2)x2-24mnxy+(4-12n2)y2=0.

兩邊同除以x2,得

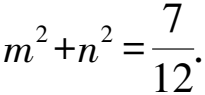
③

視角4 此題中直線OA,OB都經過原點這個定點,容易聯想到直線的參數方程.

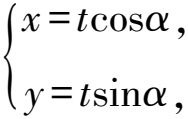
(3cos2α+4sin2α)t2-12=0.

由t的幾何意義知:

品質得分在54.70以上的為優質一級烤鴨，市售優質烤鴨中檢測到的9種雜環胺總含量水平為5 757.02～6 859.31ng·g-1。

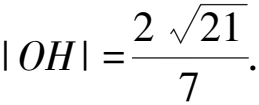
視角5題中A,B兩點都在橢圓上,故可以考慮利用橢圓的參數方程來設出A,B兩點的坐標.

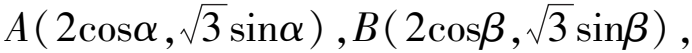
所以4cosαcosβ+3sinαsinβ=0.

從而16cos2αcos2β=9sin2αsin2β.

④

即16cos2αcos2β=9(1-cos2α)(1-cos2β).

又因OA2=4cos2α+3sin2α=3+cos2α,

OB2=4cos2β+3sin2β=3+cos2β,

故由三角形等面積法得

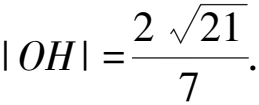
視角6 此題中直線OA,OB都經過原點這個定點,從而OA,OB與ρA,ρB相關聯,因此使用極坐標方程相比參數方程更減少其運算量.

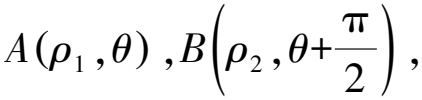
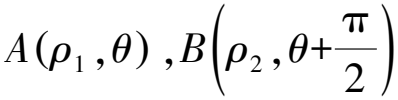
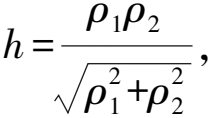
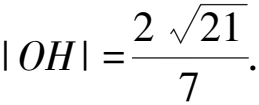
3 拓展推廣

一題多解可以培養學生全面分析問題的能力、綜合運用知識的能力,以及數學思維能力.教師不能只局限于對題目的具體解答,還應引導學生對問題進行深層次的探究及引申,充分挖掘題目的內涵和外延,使學生能夠用更高的觀點去看待問題.細品此題的結論,它對于一般的橢圓是否仍然成立呢?對于雙曲線及拋物線有無類似的結論呢?此題是否可以引申產生其它結論呢?基于以上思考,我們可以得到以下幾個一般性結論.

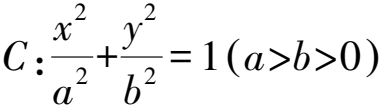
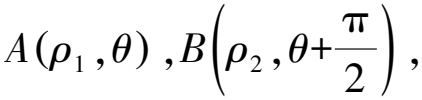
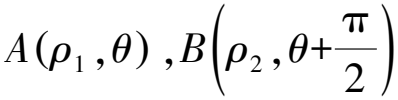
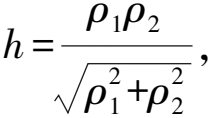
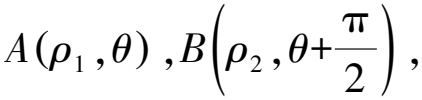
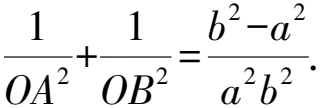
故原點到直線AB的距離為

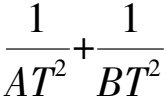
這里用直線的參數方程易證.略.

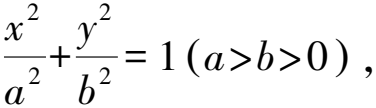
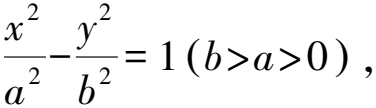
運用類比推理,對于拋物線,是否也有類似的結論呢?

結論6 已知拋物線C:y2=2px(p>0),A,B是異于頂點的兩動點,且OA⊥OB,OM⊥AB,并與AB相交于點M,則點M的軌跡方程(x-p)2+y2=p2,且(S△AOB)min=4p2.

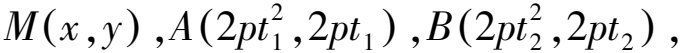
因為OA⊥OB,

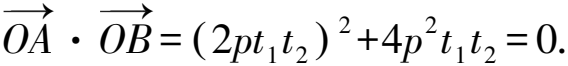
解得t1t2=-1.

⑤

又因為OM⊥AB,

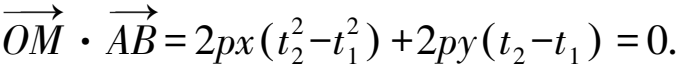
即x(t2+t1)+y=0.

⑥

由A,B,M三點共線,從而有

化簡,得y(t1+t2)-2pt1t2-x=0.

將⑤⑥代入得到

x2+y2-2px=0.

即點M的軌跡方程為(x-p)2+y2=p2.

由上述推理知

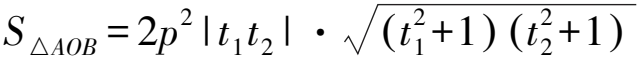
即(S△AOB)min=4p2.

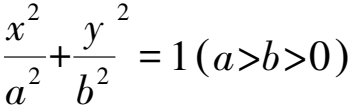
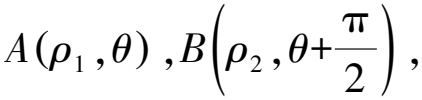
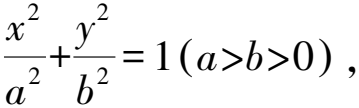
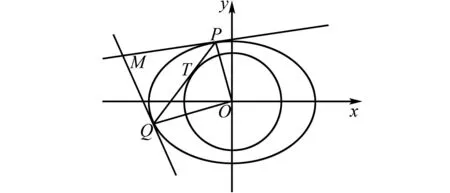
圖1 結論8示意圖

證明不妨設l與圓x2+y2=r2相切的切點為(rcosθ,rsinθ),則此切線方程為

cosθ·x+sinθ·y=r.

⑦

再設兩條切線的交點M(x0,y0),則過點M作橢圓的兩條切線,從而切點弦所在直線方程為

⑧

顯然方程⑦⑧為同一條直線的方程,故有