中學(xué)數(shù)學(xué)教材中圓周率內(nèi)容的教育價(jià)值與教學(xué)建議*

摘要：現(xiàn)行初高中數(shù)學(xué)教材中的圓周率內(nèi)容主要有劉徽“割圓術(shù)”、布豐投針試驗(yàn)、圓周率的估算以及圓面積和周長(zhǎng)的計(jì)算等，分布在多個(gè)知識(shí)領(lǐng)域（主題），主要分布在閱讀材料和習(xí)題中。這些內(nèi)容蘊(yùn)含極限和遞推思想、統(tǒng)計(jì)與概率思想、微分思想、求實(shí)精神、創(chuàng)新精神、統(tǒng)一美、簡(jiǎn)潔美、奇異美等。教學(xué)時(shí)要注意：梳理數(shù)學(xué)發(fā)展脈絡(luò)，讓整體感知與深度探究相結(jié)合；開(kāi)展數(shù)學(xué)主題教學(xué)，讓橫向聯(lián)系與縱向貫通相結(jié)合；優(yōu)化內(nèi)容表征形式，讓顯性呈現(xiàn)與隱性滲透相結(jié)合。

關(guān)鍵詞：中學(xué)數(shù)學(xué)；圓周率；教育價(jià)值；數(shù)學(xué)史；主題教學(xué)

圓周率（圓的周長(zhǎng)與直徑之比）是數(shù)學(xué)中最重要的一個(gè)常數(shù)，與數(shù)學(xué)多個(gè)分支中的眾多內(nèi)容有著豐富的聯(lián)系。人類(lèi)對(duì)圓周率的認(rèn)識(shí)與探索，有著悠久的歷史和漫長(zhǎng)的過(guò)程，積淀了厚重的數(shù)學(xué)文化。學(xué)生在小學(xué)高年級(jí)的數(shù)學(xué)學(xué)習(xí)中初步認(rèn)識(shí)了圓周率后，在中學(xué)的數(shù)學(xué)學(xué)習(xí)中還會(huì)進(jìn)一步認(rèn)識(shí)圓周率。本文嘗試在梳理現(xiàn)行初高中數(shù)學(xué)教材中圓周率內(nèi)容的基礎(chǔ)上，剖析其教育價(jià)值，給出相應(yīng)的教學(xué)建議，供中學(xué)數(shù)學(xué)教學(xué)參考。

一、 中學(xué)數(shù)學(xué)教材中的圓周率內(nèi)容

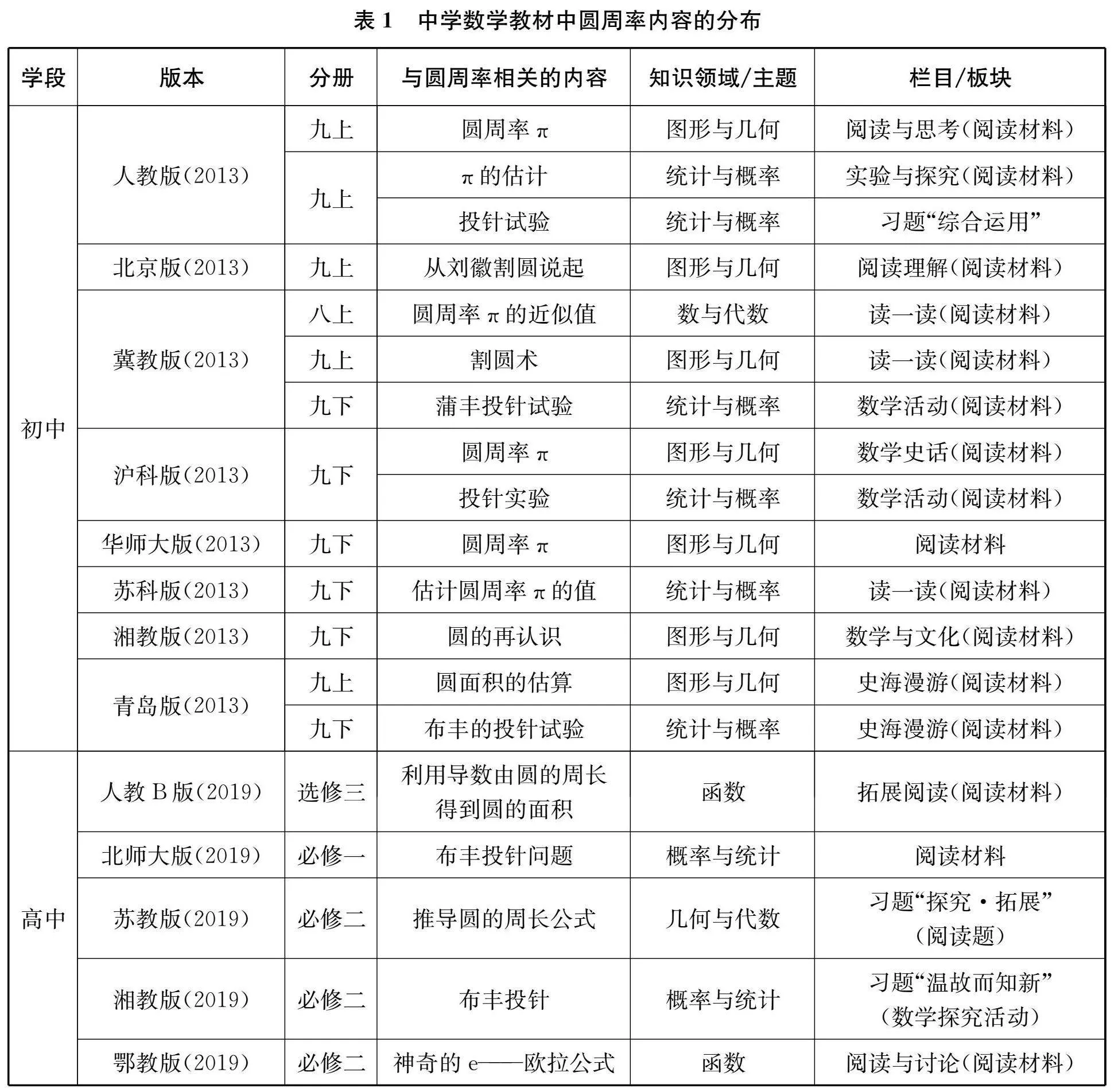
現(xiàn)行初高中數(shù)學(xué)教材中圓周率內(nèi)容的分布如下頁(yè)表1所示。由此可知，圓周率內(nèi)容主要有劉徽“割圓術(shù)”、布豐投針試驗(yàn)、圓周率的估算以及圓面積和周長(zhǎng)的計(jì)算等，分布在圖形與幾何、幾何與代數(shù)、數(shù)與代數(shù)、函數(shù)以及統(tǒng)計(jì)與概率等知識(shí)領(lǐng)域（主題），具體涉及正多邊形和圓、弧長(zhǎng)和扇形面積、空間圖形的表面積和體積、實(shí)數(shù)、求導(dǎo)法則及其應(yīng)用以及用頻率估計(jì)概率、事件的概率等知識(shí)內(nèi)容；同時(shí)，主要分布在閱讀材料性質(zhì)的欄目中，少數(shù)分布在習(xí)題性質(zhì)的板塊中。

二、 圓周率內(nèi)容的教育價(jià)值

（一） 思想價(jià)值

1. 蘊(yùn)含極限和遞推思想

多版教材都以閱讀材料的形式介紹圓周率，闡述圓周率估算的發(fā)展過(guò)程。其中，劉徽創(chuàng)立的“割圓術(shù)”是非常重要的方法，蘊(yùn)含了深刻的數(shù)學(xué)思想，可歸結(jié)為兩個(gè)方面：

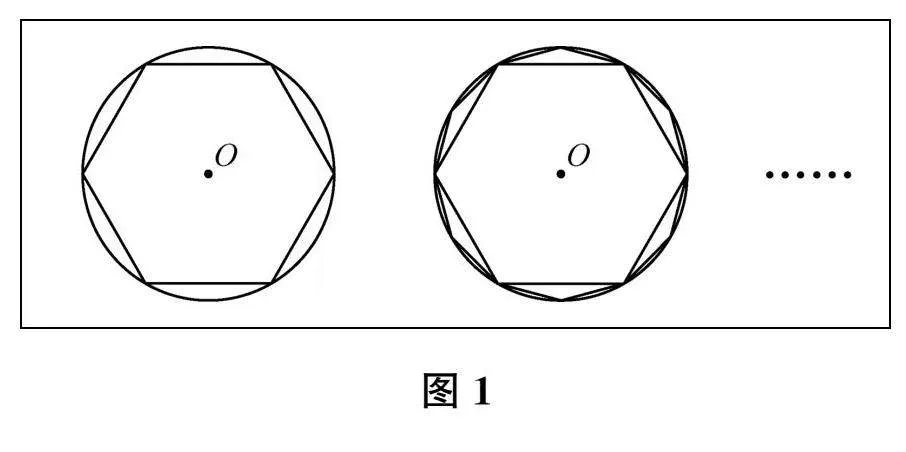
一是極限思想。“割圓術(shù)”用圓內(nèi)接正多邊形的面積來(lái)逼近圓的面積（如圖1所示），從而計(jì)算圓周率的近似值。其中，蘊(yùn)含了化歸（化圓為方）和極限（不斷逼近）的思想。相對(duì)而言，極限思想在中學(xué)數(shù)學(xué)內(nèi)容中體現(xiàn)得比較少。其實(shí)，極限是數(shù)學(xué)的重要思想。在中學(xué)教學(xué)中滲透極限思想，能充分拓展學(xué)生的想象空間，讓學(xué)生體會(huì)有限與無(wú)限的意義及轉(zhuǎn)化，在有限中認(rèn)知無(wú)限，從而認(rèn)識(shí)量變到質(zhì)變的過(guò)程，感受數(shù)學(xué)的嚴(yán)謹(jǐn)性。

……

二是遞推思想。劉徽從圓的內(nèi)接正六邊形出發(fā)，對(duì)每邊做二分，以此計(jì)算正多邊形的面積。如圖2所示，設(shè)圓的半徑r=1，AB、AC分別為圓內(nèi)接正n邊形和正2n邊形的邊長(zhǎng)，且AB=an，AC=a2n，則AP

=12an，PC=1-OP=1-1-14a2n，a2n=AP2+PC2=2-4-a2n，最終求得面積S2n=12nan（n=3×2m，m=1，2，3，…）。

可見(jiàn)，圓內(nèi)接正多邊形的面積是借助邊長(zhǎng)的遞推公式獲得的，這體現(xiàn)了遞推的思想。

因此，不必計(jì)算每個(gè)正多邊形的面積，這顯著地加快了正多邊形面積對(duì)圓面積的逼近速度。理論上，利用“割圓術(shù)”能將π的近似值計(jì)算到任意精度。

2. 蘊(yùn)含統(tǒng)計(jì)與概率思想

在圓周率估算的發(fā)展過(guò)程中，數(shù)學(xué)家還創(chuàng)造性地采用了統(tǒng)計(jì)與概率的方法。其中，“布豐投針試驗(yàn)”是用幾何形式表達(dá)概率問(wèn)題的首例，開(kāi)創(chuàng)了用隨機(jī)數(shù)據(jù)處理確定性數(shù)學(xué)問(wèn)題的方法。該試驗(yàn)實(shí)際上是求投針與平行線(xiàn)相交的概率。如圖3所示，在畫(huà)有間距為a的兩條平行線(xiàn)的白紙上隨意扔一根長(zhǎng)度為l（llt;a）的針，記落下后針的中點(diǎn)為M，M與最近的平行線(xiàn)距離為x，針與此線(xiàn)的夾角為φ，則0≤x≤a2，0≤φl(shuí)t;π。要使針與此線(xiàn)相交，需要x≤l2sin φ。作出x與φ關(guān)系的圖像，如圖4所示。利用幾何概型概率計(jì)算公式，可以求得概率p=2aπ∫π0l2sin φdφ=2lπa。由此可以推出π=2lpa。那么，當(dāng)兩條平行線(xiàn)的間距a和針的長(zhǎng)度l確定后，只要利用頻率估計(jì)概率，就可估算出π的值。在試驗(yàn)過(guò)程中，學(xué)生能感受到頻率的穩(wěn)定性：隨著試驗(yàn)次數(shù)增多，頻率在概率附近擺動(dòng)的幅度會(huì)減小。

此外，人教版和蘇科版初中數(shù)學(xué)教材還介紹了一種新的求π近似值的方法：如圖5所示，隨機(jī)撒一把米在畫(huà)有一個(gè)正方形及其內(nèi)切圓的白紙上，統(tǒng)計(jì)落在圓內(nèi)的米粒數(shù)m和落在正方形內(nèi)的米粒數(shù)n，計(jì)算頻率mn從而估算π的值。這種方法也體現(xiàn)了統(tǒng)計(jì)與概率的思想。

3. 蘊(yùn)含微分思想

人教B版高中數(shù)學(xué)教材中的一個(gè)閱讀材料，介紹了“利用導(dǎo)數(shù)由圓的周長(zhǎng)得到圓的面積”的方法。如圖6所示，設(shè)半徑為r時(shí)圓的面積為S，半徑增加Δr時(shí)圓的面積增加ΔS。當(dāng)Δr足夠小時(shí)，ΔS近似地等于長(zhǎng)2πr、寬Δr的矩形的面積，即ΔS≈2πrΔr，故ΔSΔr≈2πr。令Δr→0，可得S′=2πr。又（πr2）′=2πr，可得S=πr2。這個(gè)方法揭示了圓的周長(zhǎng)和圓的面積的實(shí)質(zhì)性聯(lián)系。它實(shí)質(zhì)上是微元法，即取對(duì)象的微小變量來(lái)處理；蘊(yùn)含著微分的思想，能有效解決曲線(xiàn)問(wèn)題（化曲為直）。

（二） 精神價(jià)值

1. 蘊(yùn)含求實(shí)精神

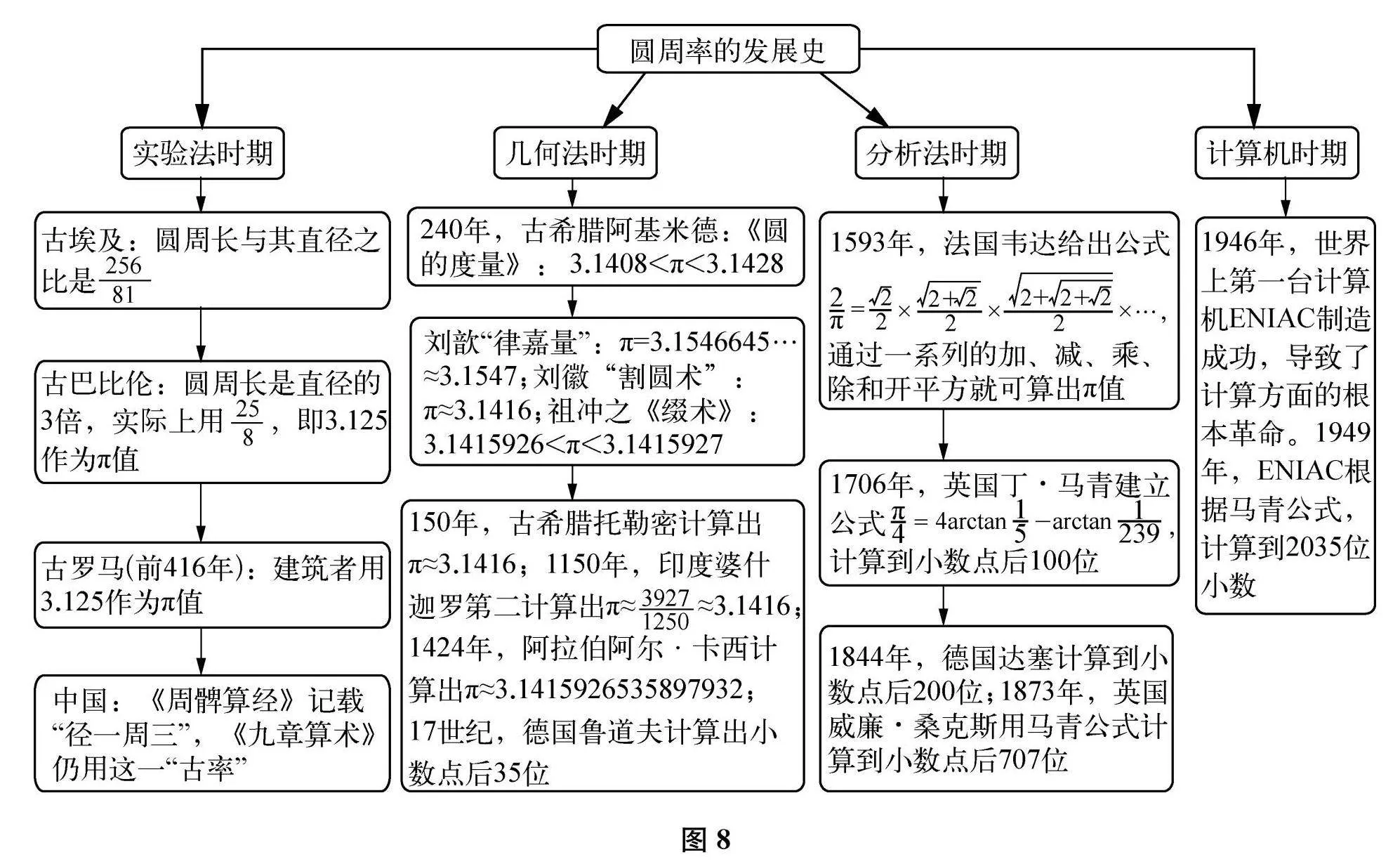
圓周率估算的發(fā)展過(guò)程（如下頁(yè)圖7所示）

凝聚了數(shù)學(xué)家的求真務(wù)實(shí)精神。從我國(guó)現(xiàn)存最早的數(shù)學(xué)典籍《周髀算經(jīng)》記載的“周三徑一”到古希臘托勒密的改進(jìn)；之后劉徽創(chuàng)立“割圓術(shù)”，最初算到192邊形，得到近似值3.14，認(rèn)為不夠精確，最終算到3072邊形，得到近似值3.1416；祖沖之繼續(xù)運(yùn)用“割圓術(shù)”，更是求得3.1415926lt;πl(wèi)t;3.1415927，并得到兩個(gè)近似分?jǐn)?shù)，即約率227和密率355113；再后隨著數(shù)學(xué)的發(fā)展，π的估算越來(lái)越精確。可以說(shuō)，正是由于數(shù)學(xué)家的求真務(wù)實(shí)精神，才有了璀璨的數(shù)學(xué)文化。

2. 蘊(yùn)含創(chuàng)新精神

數(shù)學(xué)是一門(mén)富有創(chuàng)造性的學(xué)科。數(shù)學(xué)家通過(guò)發(fā)現(xiàn)新的數(shù)學(xué)定理和解決復(fù)雜的數(shù)學(xué)問(wèn)題，展示人類(lèi)的創(chuàng)新能力。圓周率估算的發(fā)展過(guò)程可以分為四個(gè)時(shí)期。實(shí)驗(yàn)法時(shí)期，人們憑借生活經(jīng)驗(yàn)，發(fā)現(xiàn)圓的周長(zhǎng)總是其直徑的3倍多。幾何法時(shí)期，阿基米德利用內(nèi)接正多邊形與外切正多邊形“內(nèi)外相夾逼近”計(jì)算圓周長(zhǎng)，從而獲得圓周率；劉徽首創(chuàng)“割圓術(shù)”，將圓與正多邊形結(jié)合起來(lái)，用直線(xiàn)解決曲線(xiàn)問(wèn)題，揭開(kāi)了無(wú)限世界的神秘面紗；祖沖之在此基礎(chǔ)上計(jì)算到小數(shù)點(diǎn)后7位。分析法時(shí)期，數(shù)學(xué)家用微積分方法把圓周率表示成無(wú)窮級(jí)數(shù)、無(wú)窮乘積、連分?jǐn)?shù)的形式，進(jìn)而計(jì)算圓周率。計(jì)算機(jī)的出現(xiàn)使圓周率的計(jì)算進(jìn)入新階段，成為檢驗(yàn)計(jì)算機(jī)精確性和可靠性的手段。追溯這一發(fā)展過(guò)程，可以發(fā)現(xiàn)，每一次突破都經(jīng)歷了思維的創(chuàng)新。

（三） 美學(xué)價(jià)值

1. 蘊(yùn)含統(tǒng)一美

自然界原本就是統(tǒng)一的。無(wú)論怎么畫(huà)圓，圓的周長(zhǎng)與直徑的比不變，統(tǒng)一于π；π是無(wú)限不循環(huán)小數(shù)，數(shù)值在不斷延伸，卻又永遠(yuǎn)無(wú)法被完全表示。歐拉公式eiπ+1=0將數(shù)學(xué)中看起來(lái)不相關(guān)的重要常數(shù)（自然對(duì)數(shù)的底、虛數(shù)單位、圓周率以及1、0）統(tǒng)一起來(lái)，同時(shí)將指數(shù)函數(shù)的定義域擴(kuò)大到復(fù)數(shù)域，建立了三角函數(shù)和指數(shù)函數(shù)的聯(lián)系，被譽(yù)為“數(shù)學(xué)中的天橋”。數(shù)學(xué)中這種完美的統(tǒng)一激發(fā)了人類(lèi)思維的極限。

2. 蘊(yùn)含簡(jiǎn)潔美

圓周率計(jì)算方法的不斷優(yōu)化，充分體現(xiàn)了對(duì)簡(jiǎn)潔美的追求，例如遞推方法的引入。此外，在不斷探索中，人們認(rèn)識(shí)到圓周率是無(wú)限不循環(huán)小數(shù)。然而，在用符號(hào)π專(zhuān)門(mén)表示之前，其名稱(chēng)和數(shù)值都沒(méi)有統(tǒng)一，表示和計(jì)算顯得異常煩瑣；不同時(shí)期所選的符號(hào)及表示的含義也不盡相同，很不利于國(guó)際交流。1706年，英國(guó)數(shù)學(xué)家威廉·瓊斯首先使用符號(hào)π表示圓周率。［1］之后，在歐拉的倡導(dǎo)下，π成為國(guó)際通用符號(hào)。圓周率符號(hào)的確立，使圓的周長(zhǎng)和面積公式有了更簡(jiǎn)潔的表達(dá)方式。

3. 蘊(yùn)含奇異美

圓周率計(jì)算方法（表示方式）的不斷更新，還充分體現(xiàn)了數(shù)學(xué)的奇異美，激發(fā)著人們的探索欲，使人們對(duì)圓的性質(zhì)有了更深的認(rèn)識(shí)。除了各種無(wú)窮的表達(dá)式，最典型的莫過(guò)于統(tǒng)計(jì)與概率方法。相傳，布豐曾拿出一張預(yù)先畫(huà)有多條等距離平行線(xiàn)的紙，抓起一大把長(zhǎng)度是平行線(xiàn)間隔一半的小針，邀請(qǐng)客人把這些小針一根一根地往紙上投，并記錄小針與平行線(xiàn)相交的次數(shù)。最后，他宣布：“共記錄投針2212次，其中與平行線(xiàn)相交704次。2212與704的比值3.142是圓周率π的近似值！”客人無(wú)不感到不可思議而大聲贊嘆。

三、 圓周率內(nèi)容的教學(xué)建議

（一） 梳理數(shù)學(xué)發(fā)展脈絡(luò)，讓整體感知與重點(diǎn)探究相結(jié)合

教材中的圓周率內(nèi)容比較分散，不利于學(xué)生理解，尤其是不利于學(xué)生感悟其中的思想價(jià)值、精神價(jià)值和美學(xué)價(jià)值。因此，教師要系統(tǒng)地梳理圓周率知識(shí)的發(fā)展脈絡(luò)（如圖8所示），引導(dǎo)學(xué)生在整體感知的基礎(chǔ)上，有重點(diǎn)地進(jìn)行深度探究。整體感知，主要是高效地再現(xiàn)或重構(gòu)歷史，讓學(xué)生經(jīng)歷類(lèi)似的探究過(guò)程，感受知識(shí)產(chǎn)生與發(fā)展的自然性和必要性。重點(diǎn)探究，主要是充分地挖掘教材中的相關(guān)內(nèi)容，發(fā)揮不同版本教材的編寫(xiě)優(yōu)勢(shì)，必要時(shí)借助課外書(shū)籍、信息技術(shù)等進(jìn)行拓展和優(yōu)化，從而加深學(xué)生對(duì)重點(diǎn)內(nèi)容的理解和感悟。

（二） 開(kāi)展數(shù)學(xué)主題教學(xué)，讓橫向聯(lián)系與縱向貫通相結(jié)合

教材中的圓周率內(nèi)容主要分布在閱讀材料和習(xí)題中，與主干知識(shí)聯(lián)系較弱。這常導(dǎo)致教師在教學(xué)中對(duì)圓周率內(nèi)容不夠重視或“雖然重視，但是不會(huì)使用” ［2］。對(duì)此，教師可從主題教學(xué)的角度統(tǒng)整教學(xué)內(nèi)容，融合主干知識(shí)與拓展內(nèi)容，從而既注重橫向聯(lián)系，也強(qiáng)調(diào)縱向貫通。具體地，可以采取多種整合方式，如：從古到今，追尋圓周率知識(shí)的發(fā)展過(guò)程；從現(xiàn)實(shí)、熟悉的問(wèn)題出發(fā)，回溯發(fā)展過(guò)程中的重要人物與事件；以關(guān)鍵人物或事件為線(xiàn)索，分析相關(guān)數(shù)學(xué)概念以及數(shù)學(xué)思想的演變。［3］例如，以“圓的面積”為主題展開(kāi)教學(xué)：如下頁(yè)圖9所示，從割補(bǔ)法入手，整體感知化歸思想；介紹劉徽的“割圓術(shù)”，在遞推求面積

以及圓周率的計(jì)算中感受數(shù)學(xué)的嚴(yán)謹(jǐn)，滲透極限

的思想；類(lèi)比推導(dǎo)圓的面積公式和扇形面積公式；利用導(dǎo)數(shù)求圓的周長(zhǎng)和面積，感悟微分的思想，運(yùn)用于球的表面積和體積公式推導(dǎo)［4］。

（三） 優(yōu)化內(nèi)容表征形式，讓顯性呈現(xiàn)與隱性滲透相結(jié)合

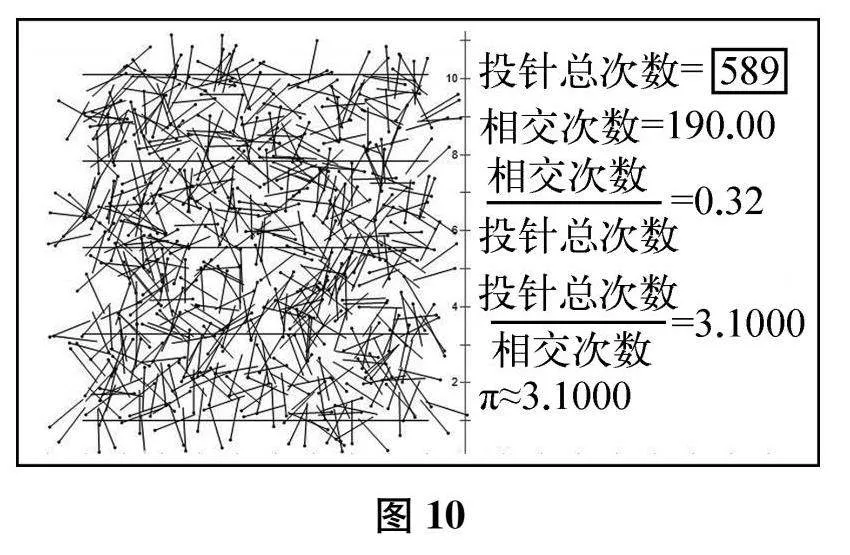
教材中的圓周率內(nèi)容主要以文字形式出現(xiàn)（附少量圖片），不利于學(xué)生理解內(nèi)容（知識(shí)），感悟價(jià)值（文化）。文化價(jià)值具有內(nèi)隱的特征，需要滲透在外顯的知識(shí)內(nèi)容中。教學(xué)中，教師要對(duì)知識(shí)內(nèi)容進(jìn)行優(yōu)化表征和裁剪重組，以更具有情境性和問(wèn)題性、更生動(dòng)和活潑的形式呈現(xiàn)，與學(xué)生的認(rèn)知基礎(chǔ)和思維特點(diǎn)相契合，讓學(xué)生在學(xué)習(xí)活動(dòng)中體悟文化價(jià)值。例如，冀教版初中數(shù)學(xué)教材中的“投針試驗(yàn)”內(nèi)容以數(shù)學(xué)文化為背景，對(duì)原有情境進(jìn)行改編，可操作性較強(qiáng)。在教學(xué)過(guò)程中，可以創(chuàng)設(shè)問(wèn)題情境引發(fā)學(xué)生深度思考：為什么要設(shè)置間隔相等的平行線(xiàn)？如何提高π估算的精度？在分析環(huán)節(jié)，要與其他“π的估計(jì)”試驗(yàn)對(duì)比，借助幾何畫(huà)板動(dòng)態(tài)呈現(xiàn)頻率與概率的關(guān)系（如圖10所示），從而促進(jìn)學(xué)生深度理解與感悟。

參考文獻(xiàn)：

［1］ F.Cajori.A History of Mathematical Notations：Vol.2［M］.La Salle：The Open Court Publishing Company，1951：913．

［2］ 羅圣潔，楊新榮.2019版高中數(shù)學(xué)必修教材的中國(guó)元素比較研究——以人教A版、北師大版、蘇教版和湘教版為例［J］.中學(xué)數(shù)學(xué)月刊，2023（1）：4046.

［3］ 李明振，龐坤.數(shù)學(xué)史融入中學(xué)數(shù)學(xué)教材的原則方式與問(wèn)題［J］.數(shù)學(xué)通報(bào)，2006（3）：2325.

［4］ 李習(xí)凡，朱勝?gòu)?qiáng).類(lèi)比思想引路，數(shù)學(xué)軟件輔助——“球的表面積和體積公式”的探究教學(xué)［J］.教育研究與評(píng)論（中學(xué)教育教學(xué)），2021（8）：9092.