移動機械臂的層級聚合建模方法研究

董方方, 楊 超, 韓 江, 張新榮

(1. 合肥工業大學 機械工程學院, 合肥 230009;2. 安徽省智能數控技術及裝備工程實驗室, 合肥 230009;3. 長安大學 陜西省高速公路施工機械重點實驗室, 西安 710064)

0 引 言

移動機械臂是通過在移動平臺上加裝一個或多個機械臂以實現協調控制的完整機械系統,相比于傳統的固定基座機械臂有更大的工作范圍,因此在工業生產、物料搬用、家政服務、搶險救援等領域有很大的應用空間．

移動機械臂雖然具有強大的功能,但由于機械臂和移動平臺這兩個系統各自的運動形式和運動特性存在較大差異,使得系統在作業過程中兩者會存在強烈的相互作用,對各自運動狀態產生相互影響,即耦合效應．耦合效應的建模分析較為困難,從而導致整體運動控制的穩定性較差．而且,這種耦合效應會伴隨著機械臂-移動平臺的質量比增大而愈加明顯．因此,通常做法是盡可能將移動平臺的質量加大來弱化這種耦合效應．表1列出了目前一些著名的機械臂-移動平臺的質量比,可以看出,質量比大部分不超過0.21,少數超過0.3．但是過大的移動平臺也會使得移動機械臂過于笨重,限制了其靈活性和工作能力．因此要實現對高質量比的移動機械臂的有效控制,高效而準確的建模方法就成為了一種前置條件．

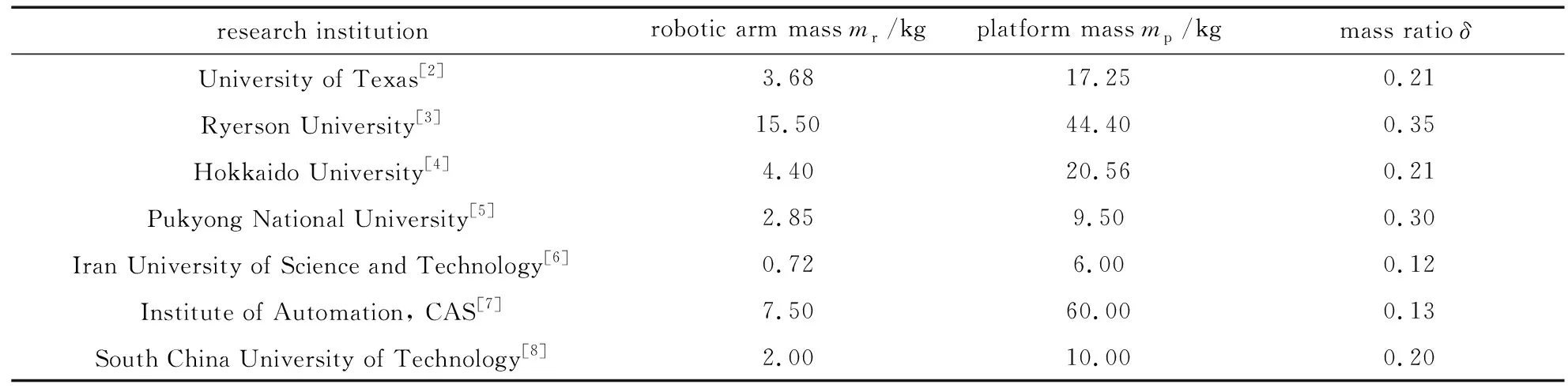
表1 機械臂-移動平臺質量比[1]

目前在移動機械臂的建模方法上有多種不同思路和解決辦法．Liu等[9]將原本耦合的移動機械臂系統分離,將耦合效應看作外部擾動,并利用Lagrange方法分別建立移動平臺和機械臂獨立的動力學方程．該方法雖然簡化了建模過程,但不能充分發揮移動作業機器人系統的動態作業能力．楊賀賀等[10]基于多體系統離散時間傳遞矩陣法,分別建立了車輪、車體柔性關節和機械臂的動力學方程,最后得到了移動柔性機械臂的整體動力學模型．該方法雖然得到了完整動力學方程,但還是要對每個分析單元進行細致的受力分析．陳良港等[11]基于單位對偶四元數法,針對冗余移動機械臂求取任務空間速度與廣義空間速度映射關系困難的問題,將移動機械臂看作一個整體建立其運動學模型．該方法雖然保證了運動學精度,但需要求解微分和逆運動學．魏麗君等[12]基于D-H算法將移動平臺看作成一個由2個移動關節和1個轉動組成的虛擬關節,并將其納入到機械臂中進行整體建模．該方法用在運動學分析中有其獨特優勢,但在動力學分析上就十分棘手．Zhong等[13]使用Lagrange方法和直接路徑法(DMP)的概念對移動機械臂進行了整體建模, 兼顧了移動機械臂內在的耦合特性, 有相對較高的建模精度, 但是增加了形式和計算的復雜性, 且仍然需要求解Lagrange乘子．

針對移動機械臂建模的復雜性和耦合性,通過應用分析力學中的U-K理論[14-16]可以對移動機械臂這一非線性的機械系統進行高效而準確的建模．該理論不同于以往的力學分析方法,通過經典建模三步法就可以完成對一個復雜機械系統的動力學建模工作．即先求得一個機械系統的無約束的動力學模型,然后將約束方程轉化為二階標準形式,之后利用UKE得到解析形式的約束力,最后可得到系統受約束的動力學方程．Huang等[17]通過對無約束的單個子系統進行聚類和級聯,利用UKE計算由約束引入的約束力,得到多體系統運動方程的封閉形式表達式．該方法表明U-K理論具有層級嵌套屬性,多層約束可以疊加聚合,這為復雜多體機械系統建模提供了一種新的實踐方法．該方法被應用到移動機械臂的建模中,不需要分析其每個子系統的受力情況,也不需要求解系統的逆解,更不需要求解Lagrange乘子,且保證了建模的準確性和簡單性．董方方等[18]基于此方法構建了雙臂機器人動力學模型,極大地減小了計算過程,并保證了模型的控制精度．韓江等[19]利用該方法高效、系統、快速地建立了2自由度冗余驅動并聯機器人的動力學解耦模型．雖然這種方法不區分完整約束或非完整約束,且簡單、通用性強,但當直接應用U-K方法時,必須保證系統在操作期間的每個時刻滿足約束條件．在實際工程中,由于各種原因,在初始階段很難滿足這些約束條件．因此,為了處理初始條件對約束可能存在的偏差,需要針對約束方程進行修正[20]．

本文根據移動機械臂的運動特點,將移動機械臂劃分為多個子系統．該方法既考慮系統所固有的耦合效應,又不失簡單性和可操作性．該方法可以獲得在不考慮任務要求下動力學建模的結構約束和任務約束下跟蹤指定軌跡的性能約束,然后便可以通過求解UKE獲得控制力的顯式的解析表達式．同時,為了解決當初始條件不滿足給定約束條件時的問題,基于Lyapunov穩定性理論,構造了修正的約束方程．最后通過仿真,驗證了建模的正確性和應對初始條件偏差的有效性．

1 Udwadia-Kalaba理論簡介

1.1 Udwadia-Kalaba基本方程

U-K方法是一種求解受約束系統約束力解析解的方法．假設一個無約束的機械系統有n個狀態變量q=[q1,q2,q3,…,qn]T,該系統無約束條件下的動力學方程可以描述為如下形式[14]:

(1)

若該系統存在m(m≤n)個約束:

(2)

m個約束可以被劃分為兩類,即完整約束和非完整約束．其包括h個完整約束

φi(q,t)=0,i=1,2,…,h,

(3)

和m-h個非完整約束

(4)

基于一致性的假設,我們可以將非完整約束(4)對時間t微分一次,將完整約束(3)對時間t微分兩次,以矩陣方程的形式推導出一組約束方程．可得到約束的二階Pfaffian標準微分形式如下[14]:

(5)

(6)

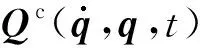
(7)

式中B(q,t)=A(q,t)M1/2(q,t),B+(q,t)為B(q,t)的Moore-Penrose廣義逆矩陣．對比式(1)和(6),可得由施加約束產生的約束力為

(8)

從上述約束力的求解過程可以看出,該方法既不需要先確定存在的具體約束條件,也不需要求解Lagrange乘子,其求解的約束力為解析解,免去了大量的求解過程,且形式簡單整潔．

1.2 Udwadia-Kalaba基本方程的層級屬性

依據式(8),外加約束力Qc中有包含Q的成分,即Qc是基于Q而得到的解析化結果．這就使得當給系統施加多個約束時,UKE可以不斷層級化地生成對應約束所產生的約束力．例如一個無約束的系統的動力學方程如下:

(9)

(10)

其中

(11)

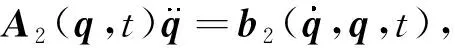
(12)

其中

(13)

當再有別的附加約束時,這種過程可以持續迭代下去．假設當到某層級時,該無約束動力學方程為

(14)

其中

(15)

1.3 建模示例

我們通過一個算例來對比層級聚合方法與傳統Lagrange方法的建模過程．假設有以下單擺系統,如圖1所示,小球的質量為m0,繩子長度為l0,繩子系在坐標系O0xy原點處,小球的坐標為(x0,y0)．小球擺動的速度為v,繩子角速度為ω,繩子與水平的夾角為β,繩子對小球施加的拉力為F．

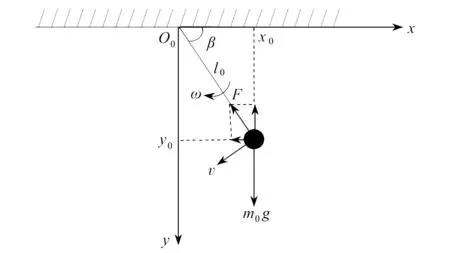
圖1 單擺系統Fig. 1 A single pendulum system

1.3.1 層級聚合建模方法

現將單擺上的小球視為一個質量為m0做自由落體運動的質點,則運動方程為

(16)

將式(16)改寫為矩陣形式:

(17)

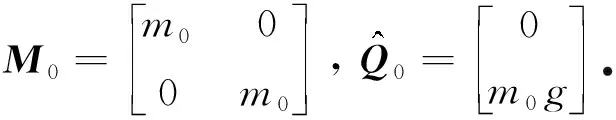
根據單擺系統的運動特點,小球受到的約束為

(18)

寫成二階Pfaffian標準微分形式為

(19)

其中

利用UKE求得約束力,并將約束力施加到式(17)的系統中,因此單擺系統動力學方程為

(20)

1.3.2 Lagrange方法

首先寫出該系統的Lagrange函數:

(21)

將式(21)代入Lagrange方程:

(22)

F-m0gsinβ=mω2l0．

(23)

因此可知F為

F=m0gsinβ+mω2l0,

(24)

計算可以得到

(25)

對應到Q0為

(26)

最后可以得到其動力學方程為

(27)

其中

從上面兩種方法的推導及分析過程可知,層級聚合方法直接對約束進行標準化處理后代入U-K方程可獲得解析形式的約束力,再與無約束系統結合即可寫出受約束系統的動力學方程．整個過程的分析簡單,無需推導,易于編程實現．而拉氏方法不僅需要復雜的運動分析,還需要對得到的Lagrange函數方程進行求解,進而得到最終的動力學方程．因此從求解全過程可知,從數據處理和運動分析的角度來看,層級聚合方法具有簡明直觀的特點．

2 基于層級聚合建模方法的移動機械臂建模

基于U-K方法的層級屬性,將所研究的移動機械臂劃分為3個子系統,即移動平臺系統和兩個機械關節系統,如圖2所示．為了方便在移動機器人上建立坐標系,下文將移動機器人抽象成簡略圖．對于3個子系統均為無約束系統時,可以更容易地得到其動力學方程．將移動平臺和機械臂切分開來是考慮到移動平臺和機械臂的差異性．此外將機械臂切分為第一、 二關節和其余關節系統, 這樣劃分的目的是減少建模過程的復雜性．

從以上介紹可知,移動機器臂是由移動平臺和機械臂所構成的復合系統．我們將選用由Mecanum輪驅動的全方向移動平臺和三關節機械臂構成的移動機械臂系統來研究移動機械臂的建模過程．選用全向移動平臺是考慮到其靈活性和保證底盤的小巧性;選用的三關節機械臂是將常規的六關節機械臂簡化為只有旋轉、下臂和上臂的三軸機械臂,而舍去其他3個對移動機械臂平臺整體控制精度和工作能力影響較小的腕關節,同時也不失研究的代表性和一般性．

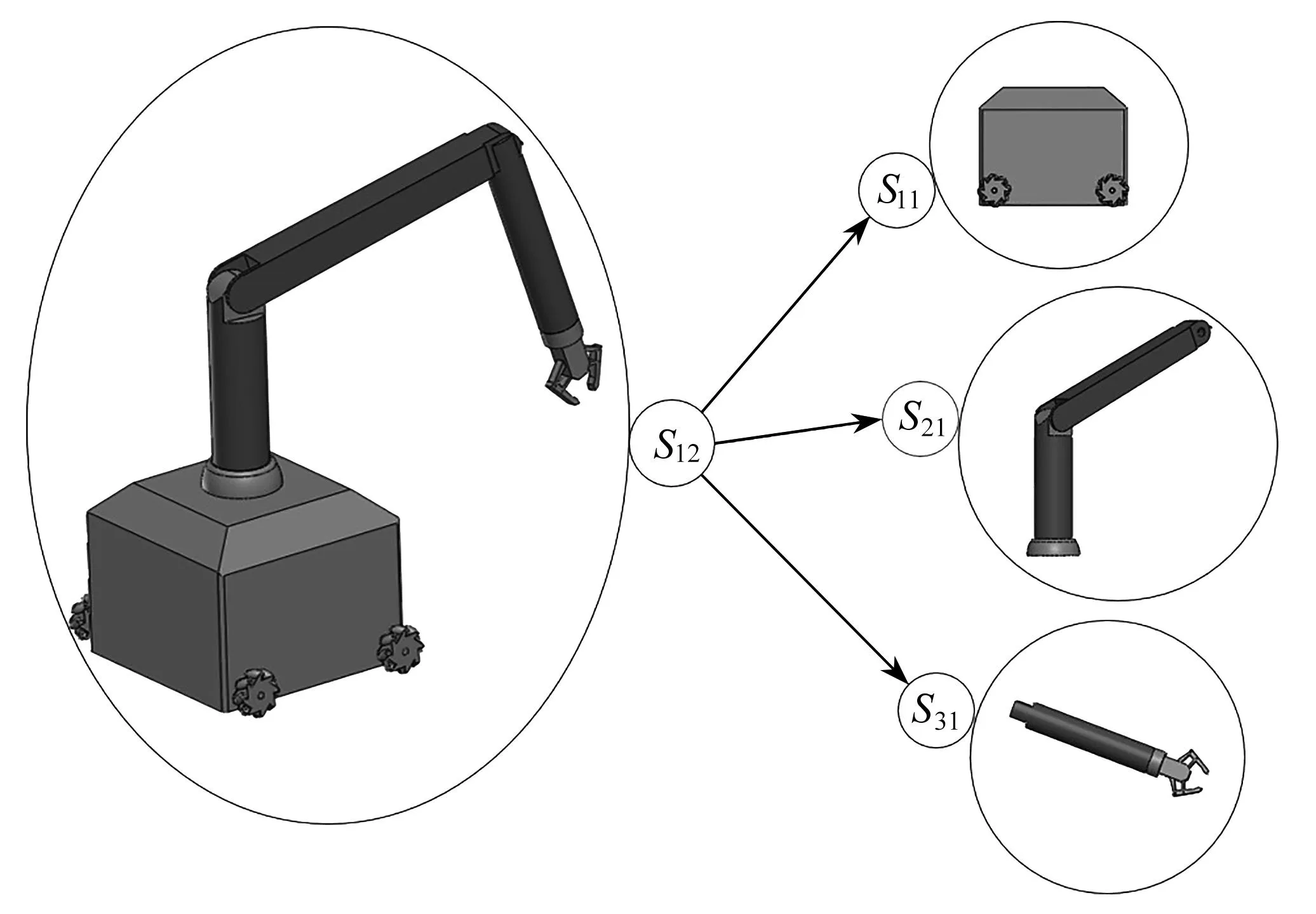
圖2 移動機械臂子系統分割圖Fig. 2 Partition of the mobile manipulator subsystem

移動機械臂運動學分析的主要任務是給出關節空間變量與位姿空間變量之間的轉換關系,即運動學正問題與運動學逆問題．圖3中的機械系統的工作裝置為三關節機械臂,因此工作裝置有三自由度．對移動機器臂進行運動學分析,首先在地面和機械裝置上建立一些坐標系．OWxWyWzW為基坐標系,OMxMyMzM為車輛坐標系,其原點OM被設置在車輛在地面上的投影,ORxRyRzR為固定在機械臂基座的坐標系,O1x1y1z1為固定在第一關節的坐標系,O2x2y2z2為固定在第二關節的坐標系,O3x3y3z3為固定在第三關節的坐標系,O4x4y4z4為固定在末端執行器的坐標系．選取機械臂的關節空間變量為:第一關節和底座之間轉角為θ1,第二關節和底座之間轉角為θ2,第三關節和第二關節之間轉角為θ3．

(28)

(29)

其中,c(θi-1)=cosθi-1,s(θi-1)=sinθi-1,c(αi-1)=cosαi-1,s(αi-1)=sinαi-1,i=1,2,3,4,θi-1為坐標系Oixiyizi相對于坐標系Oi-1xi-1yi-1zi-1的旋轉角,αi-1為坐標系Oi-1xi-1yi-1zi-1旋轉軸相對于坐標系Oixiyizi旋轉軸的旋轉角,ai-1為在xi-1方向上Oi-2xi-2yi-2zi-2和Oi-1xi-1yi-1zi-1之間的距離,di-1為在zi-1方向上Oi-2xi-2yi-2zi-2和Oi-1xi-1yi-1zi-1之間的距離．機械臂幾何參數如表2所示．

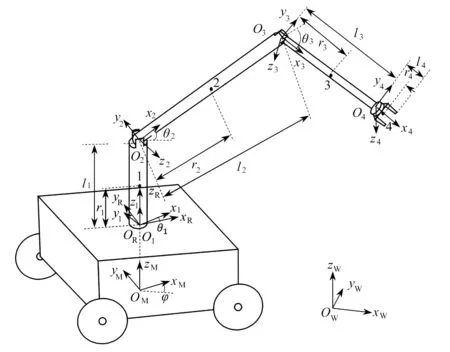
圖3 移動機械臂坐標示意圖Fig. 3 Coordinate systems for the mobile manipulator

表2 機械臂幾何參數

因此,可得在坐標系O4x4y4z4中的末端執行器尖端向量p4在機械臂坐標系O1x1y1z1中表達式p0為

(30)

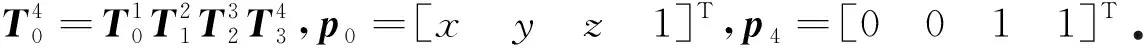
(31)

其中,c(θi)=cosθi,s(θi)=sinθi,c(θi-θj)=cos(θi-θj),s(θi-θj)=sin(θi-θj),i=1,2,3,j=2,3．機器人運動學分析中,Jacobi矩陣用來表示機器人末端執行器的線速度和角速度與各關節速度之間的轉換關系．上面求得末端位置與各個關節角度的關系后,則可得到末端執行器速度和各個關節速度的關系為

(32)

(33)

2.1 移動平臺子系統的建模

移動平臺采用了由伺服電機通過減速齒輪箱進行獨立驅動每個Mecanum輪的設置,將其置于空間坐標中對其進行運動學和動力學建模,如圖4所示．

為了表征移動平臺的位置,使用廣義坐標x,y,φ來描述其位置信息．因為該移動平臺為全向驅動,每個輪子對應了一個角位移,分別為θω1,θω2,θω3,θω4．同時由圖4可知平臺的長度和寬度分別為2L,2l,車輪半徑為Rω．其運動方程可以表示為

(34)

定義移動平臺子系統為S11,并構建其Lagrange函數為

(35)

圖4 移動平臺結構示意圖Fig. 4 Schematic diagram of the mobile platform structure

將式(35)代入到Lagrange方程中可得

(36)

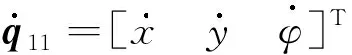
通過求解方程(36),可以得到S11的動力學方程:

(37)

M11和Q11的具體結構如下:

(38)

其中,μ表示摩擦因數．

2.2 機械臂子系統的建模

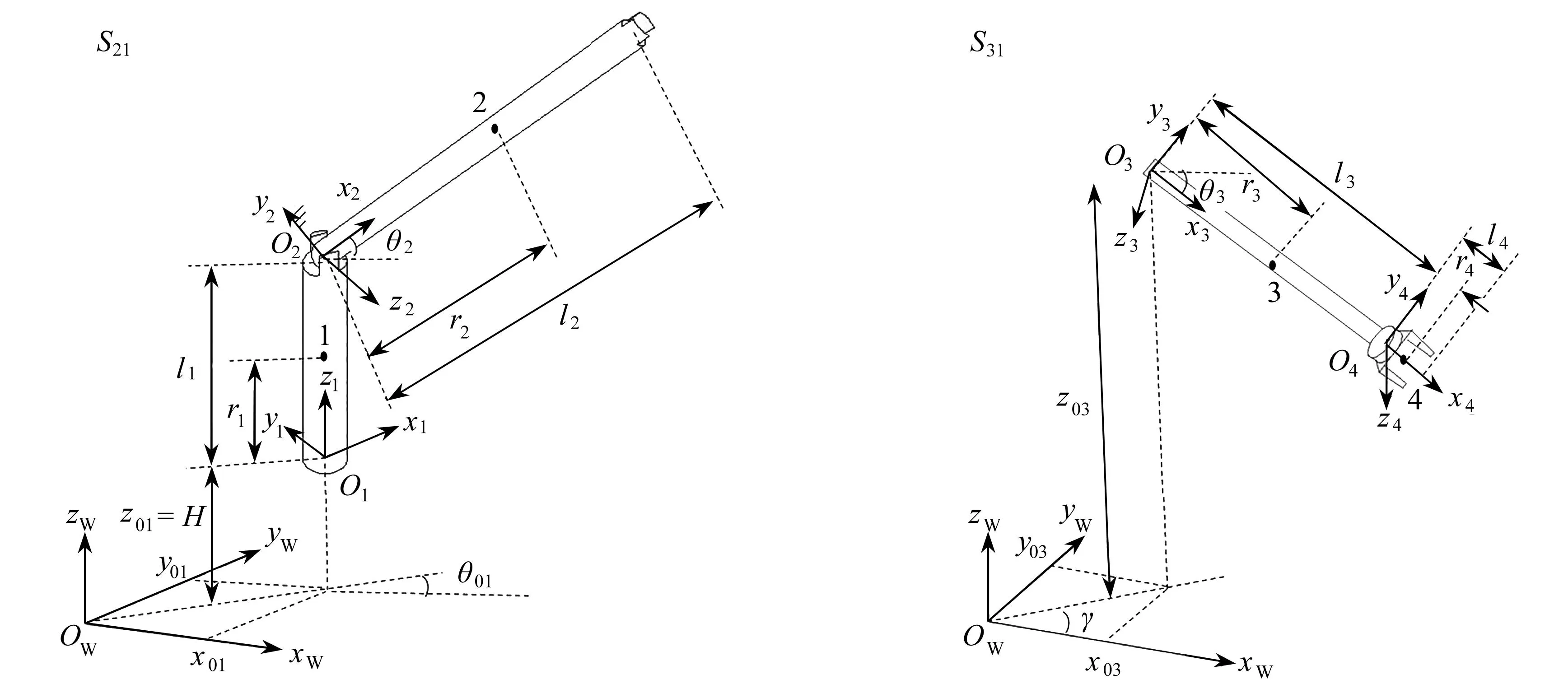
上面對機械臂部分進行了運動學分析,下面對其進行動力學建模．根據本文前面所闡述的將機械臂劃分為第一、二關節和其余關節子系統的建模思路,下面對其具體建模過程進行演示．將第一、二關節子系統定義為系統S21,其余關節子系統定義為系統S31,圖5為機械臂關節子系統示意圖．

對于系統S21,選取廣義坐標為q21=[x01y01θ01θ2]T,(x01,y01,z01)為坐標系O1x1y1z1的原點在基座標系OMxMyMzM中的空間位置．其中z01為定值,不作為其狀態變量．選取(α01,β01,θ01)為坐標系O1x1y1z1的Euler角,Euler角選取為XYZ表示方法,其中α01=0,β01=0．其子系統的Lagrange函數為L21為

(39)

其中,xc2=x01+r2cosθ01cosθ2,yc2=y01+r2sinθ01cosθ2,zc2=z01+l1+r2sinθ2,I1和I2分別為第一關節和第二關節的轉動慣量．

(a) 第一、二關節子系統(子系統S21) (b) 其余關節子系統(子系統S31) (a) The 1st and 2nd joint subsystem (subsystem S21) (b) The remaining joint subsystem (subsystem S31)

代入Lagrange方程可得

(40)

可得系統S21在無約束條件下的動力學方程,其表達式為

(41)

其中

(42)

(43)

對于系統S31,選取廣義坐標為q31=[x03y03z03γθ03]T,同樣(x03,y03,z03)為坐標系O3x3y3z3的原點在基座標系OMxMyMzM中的空間位置．選取(γ,ψ,-θ03)為坐標系O3x3y3z3的Euler角,Euler角選取為ZXZ表示方法,其中ψ=90°．

子系統S31的Lagrange函數L31可以表示為

(44)

其中

xc3=x03+r3cosθ03cosγ,yc3=y03+r3cosθ03sinγ,

zc3=z03-r3sinθ03,xc4=x03+(l3+r4)cosθ03cosγ,

yc4=y03+(l3+r4)cosθ03sinγ,zc4=z03-(l3+r4)sinθ03,

I3和I4分別為第三關節和末端執行器的轉動慣量．

將式(44)代入Lagrange方程,得

(45)

求解式(45),可得系統S31的無約束動力學方程為

(46)

式中

(47)

(48)

其中

c(θ03)=cosθ03,s(θ03)=sinθ03,c(γ)=cosγ,s(γ)=sinγ．

2.3 構建約束和系統整合

移動機械臂可以通過堆聚子系統S11,S21和S31再輔以物理上的結構約束將其重構成一個有機的完整系統．結合空間的位置關系,可以很容易得到其約束關系如下:

(49)

由式(49)可得其約束方程為

(50)

(51)

(52)

其中

q12=[xyφx01y01θ01θ2x03y03z03γθ03]T．

同時可以將子系統S11,S21和S31的矩陣M和Q集中寫成另外兩個矩陣M12和Q12,其具體構造如下:

(53)

Q12=[Q11Q21Q31]T．

(54)

利用UKE可以得到結構約束力,并獲得完整的受約束的動力學方程:

(55)

(56)

因為式(55)不是最簡形式,所以需要將其化簡．這就需要找到狀態變量q12與系統真正需要的狀態變量q=[xyφθ1θ2θ3]T之間的變換關系．除了知道式(49)所得到的關系之外,還知道θ01=γ=φ+θ1和θ03=θ3-θ2,綜合這些條件,可以得到以下關系式:

(57)

其中

(58)

(59)

則對式(55)進行化簡可得

(60)

當系統受到外部運動約束時,會對系統施加外部約束力τ,從而最后可得式(60)的最簡形式如下:

(61)

其中

τ為運動約束力．

3 初始條件偏差

在仿真中使用的系統初始條件必須滿足所需的軌跡跟蹤約束．但是,由于各種因素的存在,這種情況未必真會發生．它可能只在初始時刻被近似滿足．如果初始條件不相容,則模擬結果會出現發散．處理初始條件問題的一種方法是使用Lyapunov穩定性理論,如文獻[20]所示．

所期望的軌跡由式(2)描述．基于軌跡穩定方法,我們現在修改約束方程為

(62)

式中f(φ,t,α)是包含向量p、參數α的m維向量．式(62)必須滿足以下要求:

注1 特別地,如果約束方程是完整的,如式(3)所示,那么方程可以修改為

(63)

現在用修正式(3)作為期望的軌跡要求,通過微分過程,得到矩陣方程的形式為

(64)

經過修改,控制力為

(65)

4 仿 真

為了驗證本文所提出的層級建模方法的準確性,以及UK方法對于移動機械臂的協調控制的可實現性和適應性,將通過以下仿真過程予以說明和闡述．模擬的對象是圖2所示的移動機械臂,該機械裝置主要包括由4個Mecanum輪驅動的全向移動平臺和由3個關節和末端夾爪構成的機械臂,其具體參數如表3所示．

表3 系統動力學參數表

為了貼近實際使用場景,便于直觀地理解仿真結果,本文采用了常見的機械臂-移動平臺質量比參數．質量比參數并不影響本文的建模和仿真過程,只影響穩定性控制的難易程度．

為了驗證本文層級聚合建模方法的建模精度和準確性,對拉氏方法和層級聚合建模方法得到的模型同時施加約束(66)(約束滿足初始條件):

(66)

并比較在施加約束后每個狀態變量的數值是否一致．

圖6表示在受約束條件下兩種建模方法獲得的移動平臺軌跡隨時間的變化情況,圖7(a)和7(b)分別為層級聚合建模方法和Lagrange方法所得的機械臂各關節軌跡隨時間的變化情況,通過對比可以發現各自的運動軌跡是一致的．圖8為兩種模型下各個狀態變量的數值誤差,圖8(a)為移動平臺x方向和y方向的軌跡誤差,圖8(b)為機械臂各關節的軌跡誤差．可以發現所有結果始終為零,這說明兩種建模方法得到的計算結果完全一致,充分說明了本文建模方法與拉氏方法在建模精度和準確性上是一致的．

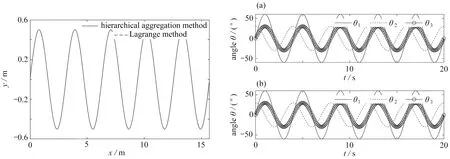
圖6 移動平臺軌跡

為對比算法的效率,采用MATLAB記錄了兩種方法的計算耗時,如圖9所示．從圖9中可以看出,層級聚合方法比拉氏方法所獲得的模型在計算效率上略有提高,但提升的幅度有限．然而,本文提出的層級聚合建模方法對于不同類型約束(完整、非完整約束)處理具有更好的一致性,都是將約束轉化為二階微分形式,再利用UKE寫出約束力的解析解．整個建模過程簡潔明確,分析步驟較少．而拉氏方法需要先求解Lagrange乘子,無法獲得解析形式的解．此外,利用層級疊加的屬性,當有新的約束增加后,本文方法只需將新的約束轉化為二階微分形式后代入UKE,不影響其他分析步驟．

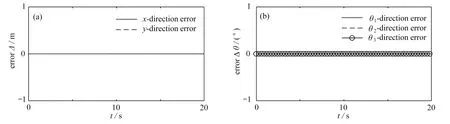
圖8 移動平臺與機械臂各自軌跡誤差Fig. 8 The respective trajectory errors of the mobile platform and the manipulator

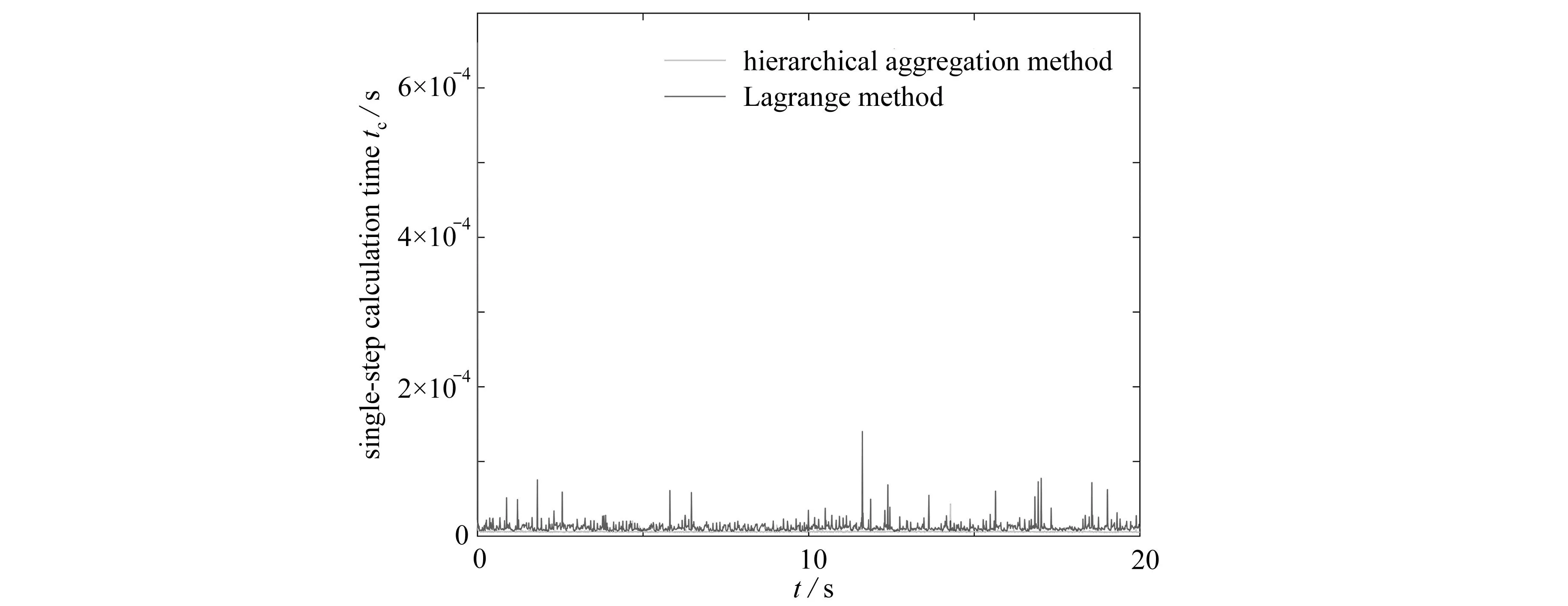
圖9 層級聚合方法與拉氏方法計算效率對比Fig. 9 Comparison of computation efficiency between the hierarchical aggregation method and the Lagrange method

同時為了證明本文算法對于處理初始條件偏差的有效性,為移動機械臂選定一組軌跡約束,讓移動平臺走正弦曲線,并且機械臂進行相對于移動平臺的畫斜圓運動,約束條件如表4所示(xmp(t),ymp(t)和zmp(t)分別為末端執行器相對于移動平臺在坐標系ORxRyRzR中三個方向上的軌跡約束時間函數)．

表4 約束條件參數

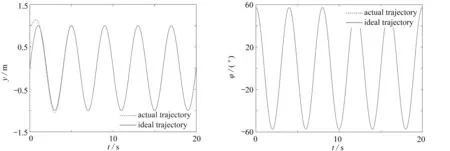
圖10—13為移動平臺和移動機械臂各自設定軌跡約束并附加任意初始條件的情況下對于理想軌跡的跟蹤情況．通過觀察可知我們選定的約束均為完整約束,所以選擇式(63)這種修正方案．表4所有約束均可寫為式(63)這種形式,這樣便可以將式子Fi(i=1,2,…,6)改寫為6個修正的約束等式．其中兩參數設置為,κm=2.5(m=1,2,3對應F1,F2,F3的修正方程),κn=2(n=4,5,6對應F4,F5,F6的修正方程),εi=1.5 (i=1,2,…,6對應F1,F2,…,F6的修正方程)．圖10(b)為機械臂相對于移動平臺的畫圓運動,可以發現在宏觀上末端執行器從較大范圍的初始條件偏差下逐漸回歸到離線軌跡上．圖10(a)為移動平臺和機械臂相對于移動平臺畫圓展開后的空間軌跡,符合一般移動機械臂協調運動模式(p1和p3分別為末端執行器初始位置和終止位置;p2和p4分別為移動平臺初始位置和終止位置)．

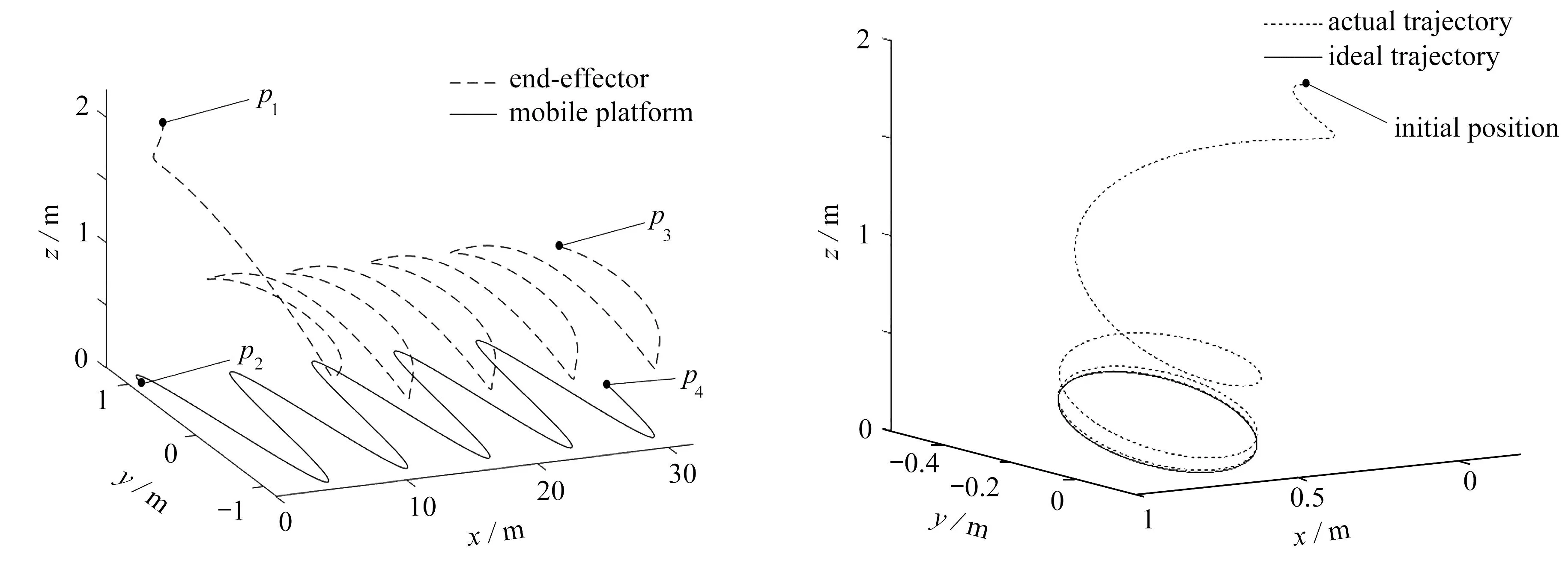
(a) 移動平臺、末端執行器空間軌跡 (b) 末端執行器相對移動平臺軌跡 (a) Spatial trajectories of the mobile platform and the end-effector (b) End-effector trajectories relative to the mobile platform

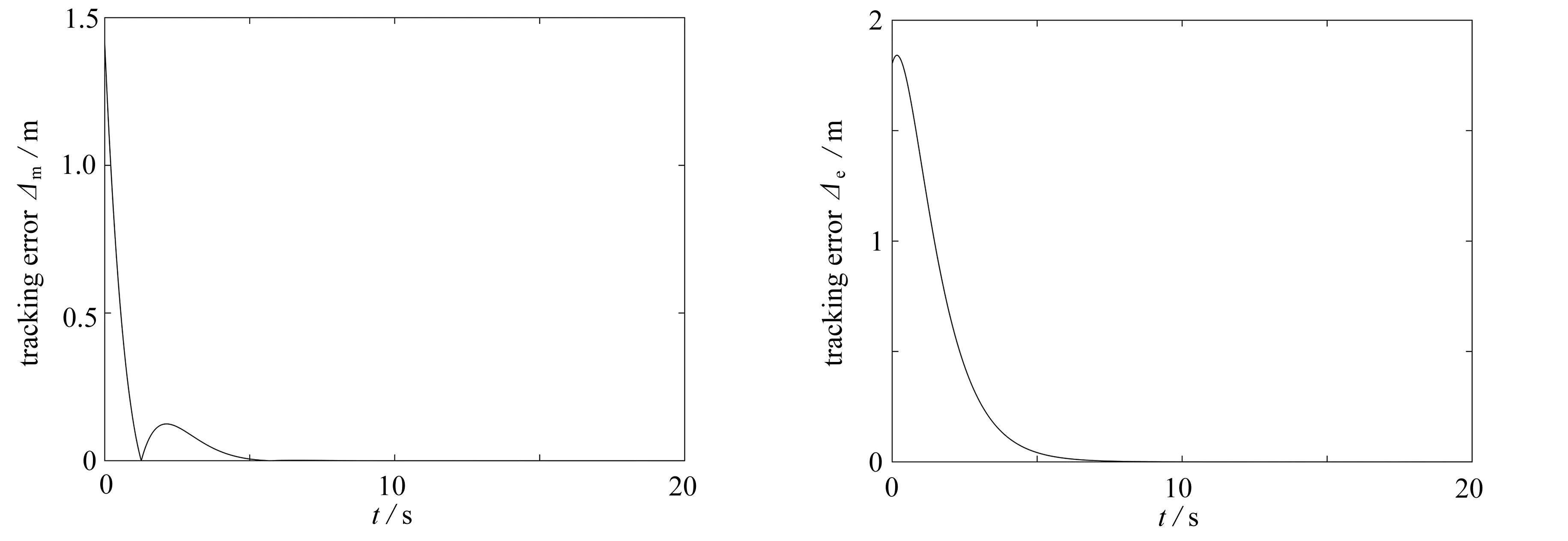
圖11為移動平臺的軌跡跟蹤情況,可以發現移動平臺在從在較大的初始條件偏差的情況下,在修正后的約束方程的約束下漸進地使得偏離的軌跡收斂于理想軌跡上．圖11(b)、(c)和(d)分別是移動軌跡在x,y方向和航向角上的跟蹤情況,也都吻合圖11(a)宏觀上所顯現的收斂情況,都在一定的時間段后達到了收斂．圖12(a)和(b)分別為移動平臺和末端執行器兩部分軌跡跟蹤誤差變化情況,可以發現移動平臺在5 s后逐漸收斂,機械臂在8 s后逐漸收斂．其中移動平臺的軌跡跟蹤誤差為4×10-4m,末端執行器移動平臺的軌跡跟蹤誤差為5×10-4m,符合軌跡跟蹤精度要求(圖12顯示的軌跡誤差均為綜合誤差)．初始時刻之所以會出現跟蹤誤差較大情況,首先因為本文特意將初始條件選取在理想軌跡之外的一點,所以使得初始時刻軌跡誤差較大;其次也是利用修正方程對理想軌跡的跟蹤使得初始時刻出現了較大的超調量,目的是使系統更快的收斂．圖13(a)中Fx和Fy分別為關節1施加在移動平臺x,y方向上的約束力, 圖13(b)中T1,T2和T3分別為關節1,2,3的內部約束力．觀察圖中數值可知,約束力沒有出現奇大情況,貼合現實的使用需求．

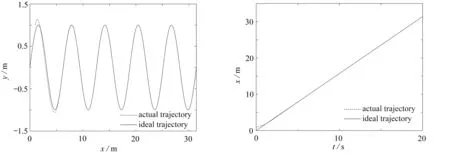
(a) 移動平臺x,y軌跡 (b) 移動平臺x方向軌跡 (a) Mobile platform x,y trajectories (b) Mobile platform x-direction trajectories

(c) 移動平臺y方向軌跡 (d) 移動平臺航向角 (c) Mobile platform y-direction trajectories (d) Mobile platform heading angle

(a) 移動平臺軌跡誤差 (b) 末端執行器相對移動平臺軌跡誤差 (a) Mobile platform trajectory errors (b) End-effector trajectory errors relative to the mobile platform

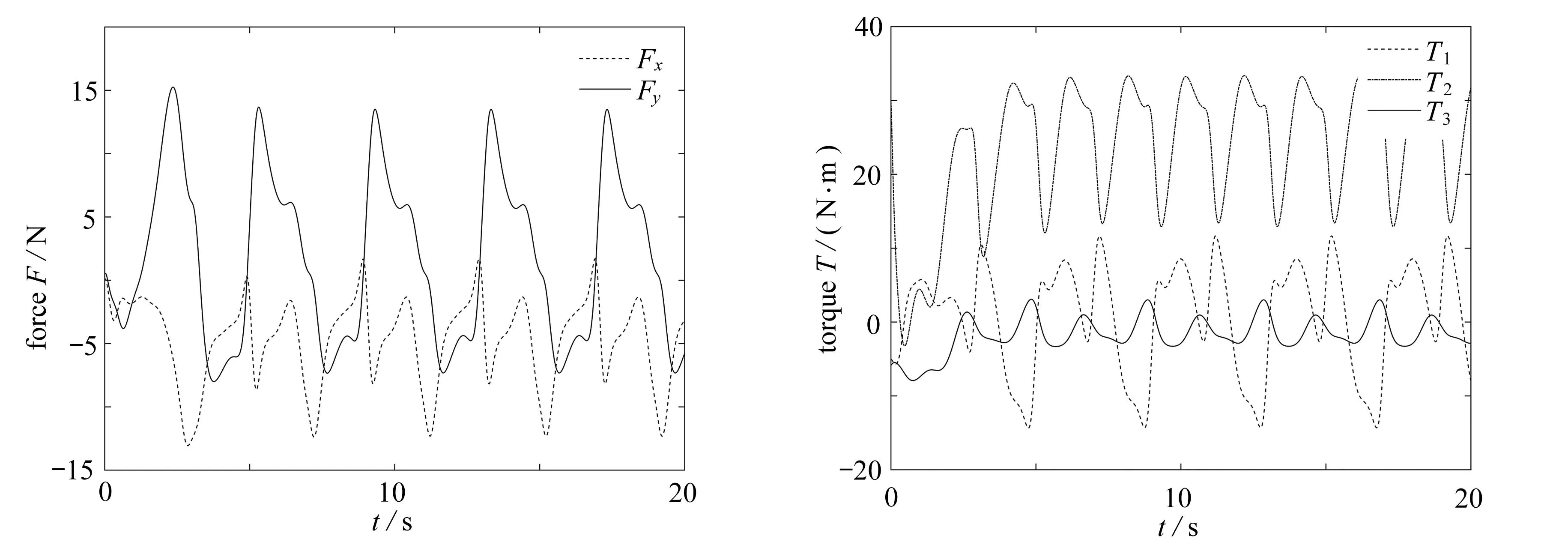
(a) 關節1施加在移動平臺x,y方向上的約束力 (b) 關節1,2,3內部約束力 (a) The forces applied to joint 1 in the x,y-directions (b) Internal constraints of joints 1,2,3 of the moving platform

5 結 論

本文首先應用了不同以往的建模方法,依據移動機械臂本身的運動特點,將移動機械臂劃分為多個子系統．該方法既考慮系統所固有的耦合效應,又不失簡單性和可操作性．該方法包含在不考慮任務要求下動力學建模的結構約束和跟蹤指定軌跡的性能約束條件下,通過求解UKE可以獲得控制力的顯式、閉合形式的解析表達式．對于機械系統在一般條件中初始條件不滿足的情況下,通過基于Lyapunov穩定性理論,將原來設定的軌跡約束規約化為修正的約束方程,以得到新的約束矩陣,并將其施加在所建立的動力學模型上達到補償初始條件偏差的目的．最后仿真結果驗證了移動平臺和機械臂在同時進行運動時,均可以滿足收斂到理想軌跡的性能需求,并實現了較高的精度要求．

致謝本文作者衷心感謝陜西省高速公路施工機械重點實驗室(長安大學)開放基金(300102252505)對本文的資助．