次表面分岔裂紋的力學行為

孫 奇, 吳金波, 江曉禹

(西南交通大學 力學與航空航天學院, 成都 610031)

0 引 言

隨著現代工業的迅速發展,各種實際的工程問題離不開斷裂理論的指導,以往研究中,多認為裂紋沿著其延長線進行擴展,卻忽略了對裂紋二次斷裂現象的研究．二次斷裂現象是指裂紋沿直線擴展之后出現方向改變的現象,裂紋分岔就是一種重要的二次斷裂現象．分岔裂紋常見于脆性材料、塑性較小的材料以及金屬應力腐蝕問題中．通過對分岔裂紋的研究,可以初步預測裂紋是否會分岔、計算分支應力強度因子等,因其具有重要的工程意義,故長期受到斷裂力學領域的關注．

從20世紀開始,國內外學者均對分岔裂紋做了大量工作,其中:Theocaris等[1]運用復勢法研究了無限各向同性彈性板上對稱分岔裂紋的平面問題,給出了分岔裂紋尖端的應力強度因子．Lam等[2]利用分布位錯技術解決了圓形夾雜物與嵌入無限彈性介質中對稱分岔裂紋之間的相互作用的問題,討論了不同模量的夾雜對分岔裂紋擴展的影響．Yan[3]利用分布位錯技術計算了無限大板中多條分岔裂紋相互作用的問題,給出了裂紋尖端附近的應力場．Yavuz等[4]把裂紋尖端位移不連續單元與恒位移不連續單元結合起來,為分岔裂紋的應力強度因子計算提供了一種更為精確的方法．Dahlan等[5]利用有限元方法研究了單軸牽引作用下二維板上的靜態對稱分支和非對稱分岔裂紋．魏華建等[6]利用擴展有限元方法(XFEM)對分岔裂紋的非尖端破壞進行了討論．Kornev等[7]采用有限元法求解雙對稱分岔裂紋,并使用Neuber Novozhilov型斷裂準則和充分斷裂準則計算得到了臨界斷裂參數．Chen等[8]在擴展有限元法的框架下,提出了一種研究復雜分岔裂紋擴展的增強擴展有限元方法．張端等[9]利用3D打印技術制作了不同形態的分岔裂紋,并研究了其在不同起裂荷載下的力學行為．

上述文獻中的主要研究方法包括數值法、有限元方法、實驗法、解析法,但其大多數研究的僅僅是在簡單荷載下的分岔裂紋,且將裂紋所在平面簡化為無窮大的情況,對于復雜荷載下的研究以及自由邊界對分岔裂紋產生影響的研究仍有所不足．本文利用分布位錯技術研究了半無限大平面內次表面分岔裂紋在復雜荷載下的力學行為．本文的主要研究內容為:根據等效應力強度因子判據,初步解釋了裂紋產生分岔的原因;計算了分岔裂紋在不同埋深、荷載比值、分支長度比值、分岔角度下分支的應力強度因子;最后,還研究了多分支分岔裂紋的情況,其結果與有限元對照良好．此外,分布位錯技術相較于有限元,略去了每次模型改變后繁瑣的網格劃分工作,只需要改變裂紋的位置參數便可進行計算,是一種便捷的研究分岔裂紋的數值方法．

1 原 理

1.1 問題描述

本文欲用理論方法(分布位錯技術)研究分岔裂紋,重點是求解分支尖端的應力強度因子,由此討論不同工況下分岔裂紋的力學行為．在圖1中考慮將分岔裂紋建模為三條相交的直裂紋,分別表示為裂紋1(即主裂紋AD)、2(即DB裂紋分支)、3(即DE裂紋分支)．a,b,c分別表示主裂紋1、分支裂紋2、分支裂紋3的裂紋半長;d表示主裂紋中心到自由邊界的距離;θB,θE分別表示分支裂紋2、3延長線與主裂紋延長線的夾角;A,B,E(為了應力強度因子表達式與斷裂韌性有所區別)表示分岔裂紋尖端;D表示分岔點．

1.2 疊加原理

基于Bueckner定理[10],將主問題分解成兩個子問題:子問題1,無裂紋時,外載在半無限彈性平面內產生應力的問題;子問題2,無外載時,半無限彈性平面內裂紋區域的刃位錯產生應力的問題．最后根據裂紋面應力條件,將以上兩個子問題聯立求解．

1.3 建立位錯密度積分方程

在半無限大板中由位錯引起的應力分量由下式給出[10-11]:

(1)

其中κ是Kolosov常數,平面應變時κ=3-4ν,平面應力時κ=(3-ν)/(1+ν);ν是Poisson比;μ是剪切模量;bx和by代表Burgers矢量在x,y方向上的分量;Gxij和Gyij是位錯影響函數,第一個下標表示Burgers矢量,后兩個下標表示應力分量,其表達式可參考文獻[11]．為了方便在局部坐標系下進行計算,需要進行以下坐標變換:

(2)

(3)

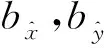
(4)

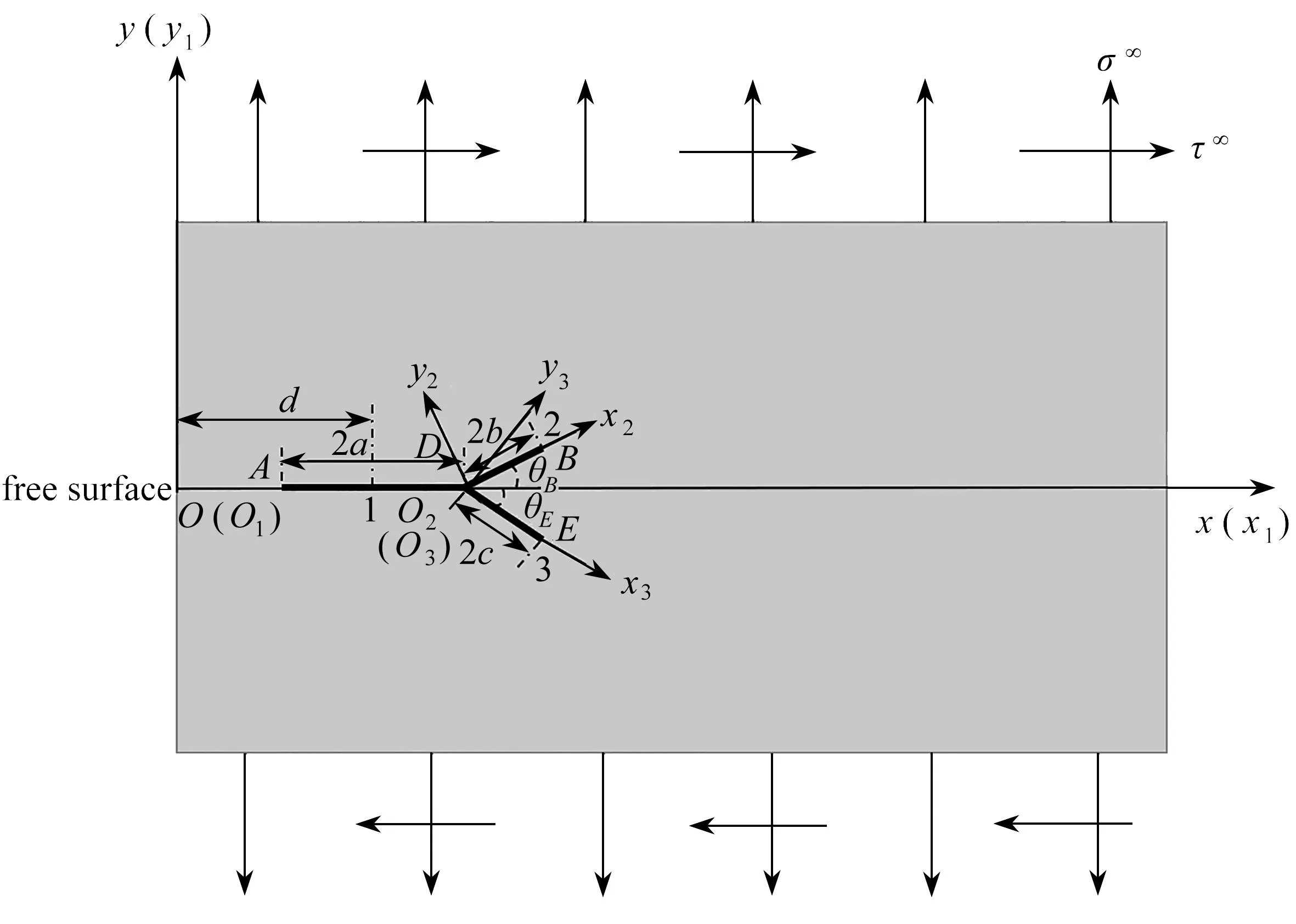
圖1 復雜荷載下的半無限平面分岔裂紋Fig. 1 The semi infinite plane bifurcating crack under complex loads

在后續的計算中只需要變化ξ,x,y,θ,θ1,就可以得到由任意局部坐標系上的位錯在任意局部坐標系上所產生的應力分量．以裂紋1對裂紋2的影響函數作為例子進行解釋,如圖2所示,其中紅色圖形代表刃型位錯列．只需進行以下替換:ξ=ξ1,x=x2cos(θB)+d+a,y=x2sin(θB),θ=0,θ1=θB即可得到．其中ξ1是裂紋1上位錯的全局橫坐標;x是裂紋2的全局橫坐標,y是裂紋2的全局縱坐標減去裂紋1的位錯全局縱坐標;θ,θB分別代表裂紋1和裂紋2坐標系的偏轉角;其余影響函數可用類似方法獲得．

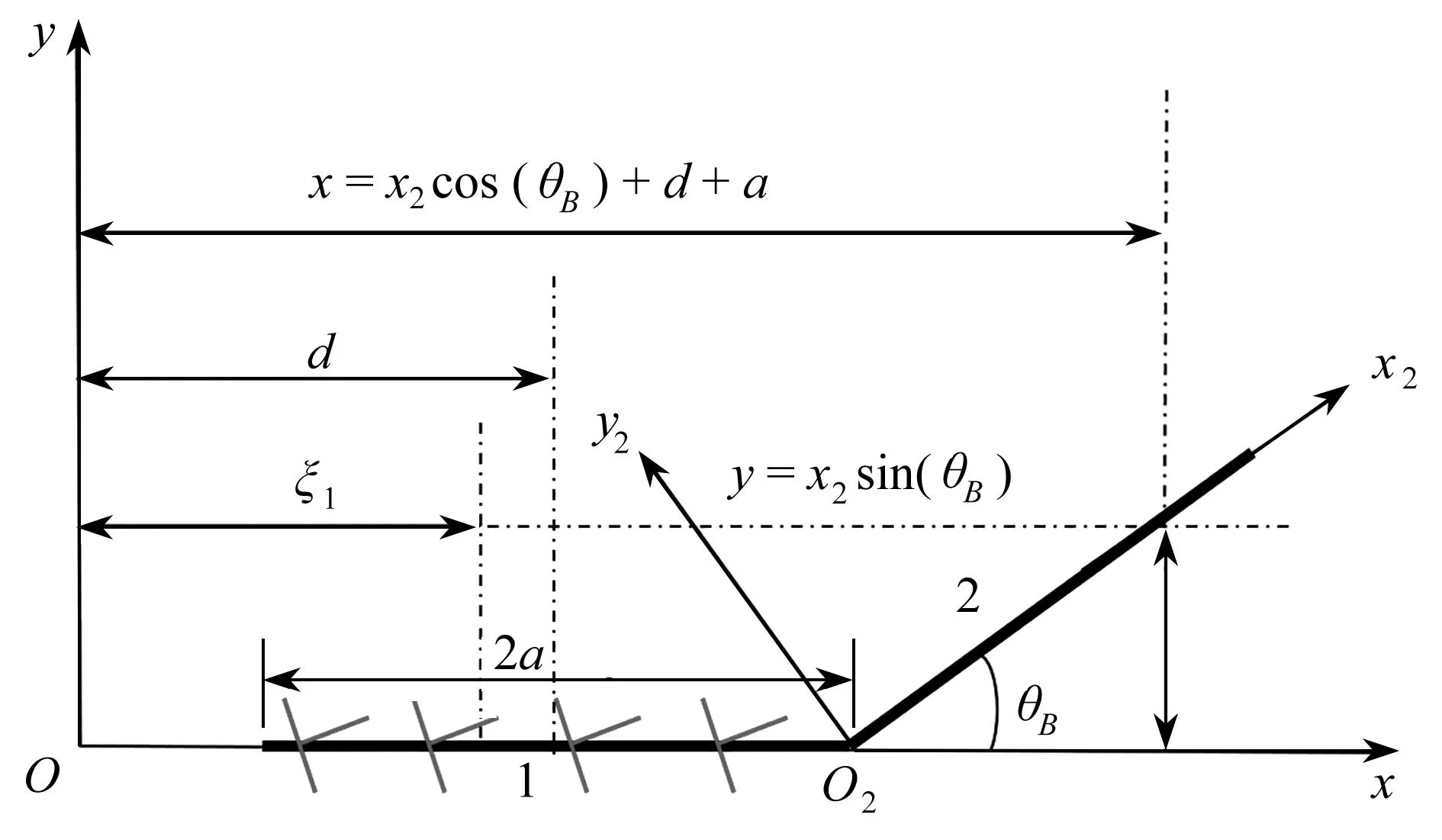
圖2 坐標變換示意圖Fig. 2 Schematic diagram of coordinate transformation

現在基于分布位錯技術,將每條裂紋視為未知的連續分布的刃位錯[11],表示為Bl(ξk),其中l=1,2分別代表x,y方向上的位錯,ξk代表第k條裂紋分布位錯的局部坐標(k=1,2,3)．因此,對于每一條裂紋而言,通過疊加包括自己在內的其他裂紋位錯所產生的應力分量與外載荷產生的應力分量,并結合裂紋面的無牽引條件,可以得到

(5)

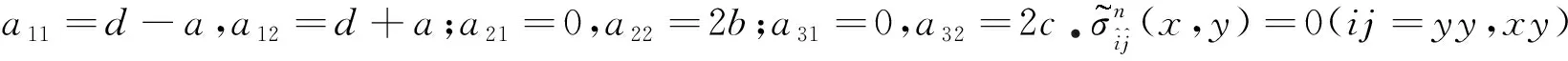
2 奇異積分方程的數值解

采用基于Gauss-Chebychev求積方法[12]的數值技術來求解積分方程組(5),首先需要對積分區域進行歸一化處理:

(6)

其中

(7)

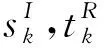
(8)

將方程(6)、(7)、(8)代入方程(5),得到離散化的方程:

(9)

方程(9)總共有6M-6個線性方程,但是總共需要求解6M個未知數,因此需要額外補充6個方程．所謂的封閉或者單值條件[12]提供了額外的兩個方程式,這兩個方程表示次表面分岔裂紋在x與y方向上的凈位錯位均為零．ak代表第k條裂紋的半長,

(10)

由于主/分支裂紋交點 (圖1中的點D)處的奇異性小于1/2,文獻[2]將分岔點處的應力強度因子處理為0,其實際可用的方程個數為6個．文獻[2]經過比對不同的方程所產生的結果,選出了其中最佳的4個額外方程如下:

(11)

其中φl(sk=±1)可以通過文獻[12]中的方法進行插值得到．至此,未知數個數與所需方程數相等,方程(9)可以得到解答．裂紋尖端的應力強度因子由φl(tk=±1)推出,例如尖端E的應力強度因子表示為

(12)

3 結 果 驗 證

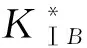
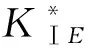
如圖3所示,對比本文理論計算的結果與已有文獻的結果,發現本文的理論計算結果與文獻計算結果相差無幾,足以說明本文理論模型的正確性,可以用于后續的計算．

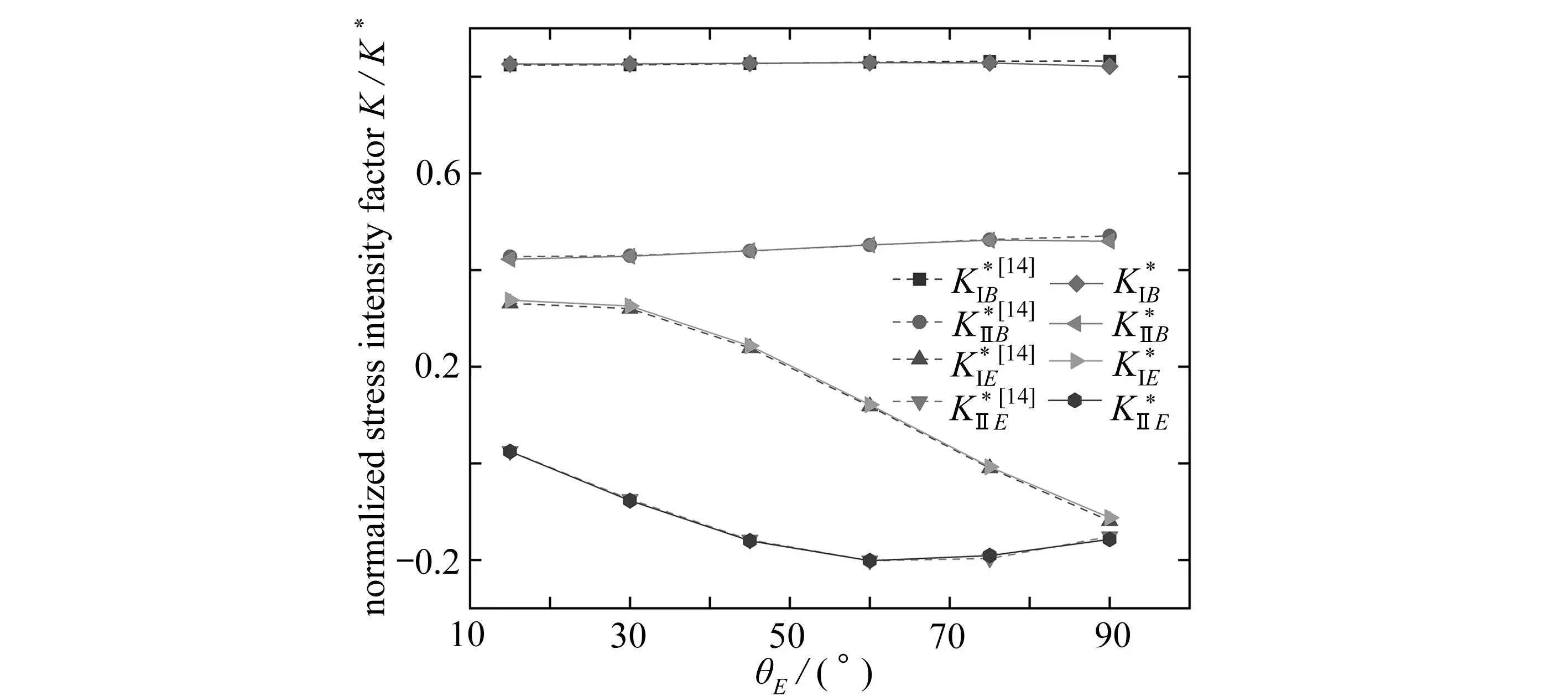
圖3 非對稱分岔裂紋的計算結果對照圖Fig. 3 Comparison of calculation results of asymmetric bifurcating crack

4 結果與分析

4.1 分岔裂紋產生的原因及過程

文獻[14]研究發現,如果根據最大周向拉應力準則判斷裂紋擴展角度,其預測的裂紋擴展角度變化過于劇烈,這與真實的實驗結果及事實不符．因此采用文獻[14]中的方法:如圖4所示,將裂紋沿各個不同的方向擴展b=0.1a,計算裂紋在不同方向上的等效應力強度因子Keff=KⅠ+|KⅡ|,將其最大值所在的角度視為裂紋下一步的擴展角度．參數設置如下:荷載τ/σ=0.1,d/a=1.5．從圖4中可以看出,Keff在-35°和20°時均出現了峰值,這說明裂紋在-35°和20°都容易發生擴展,從而導致出現分岔的情況．

4.2 埋入深度d/a對和的影響

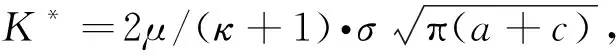
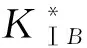
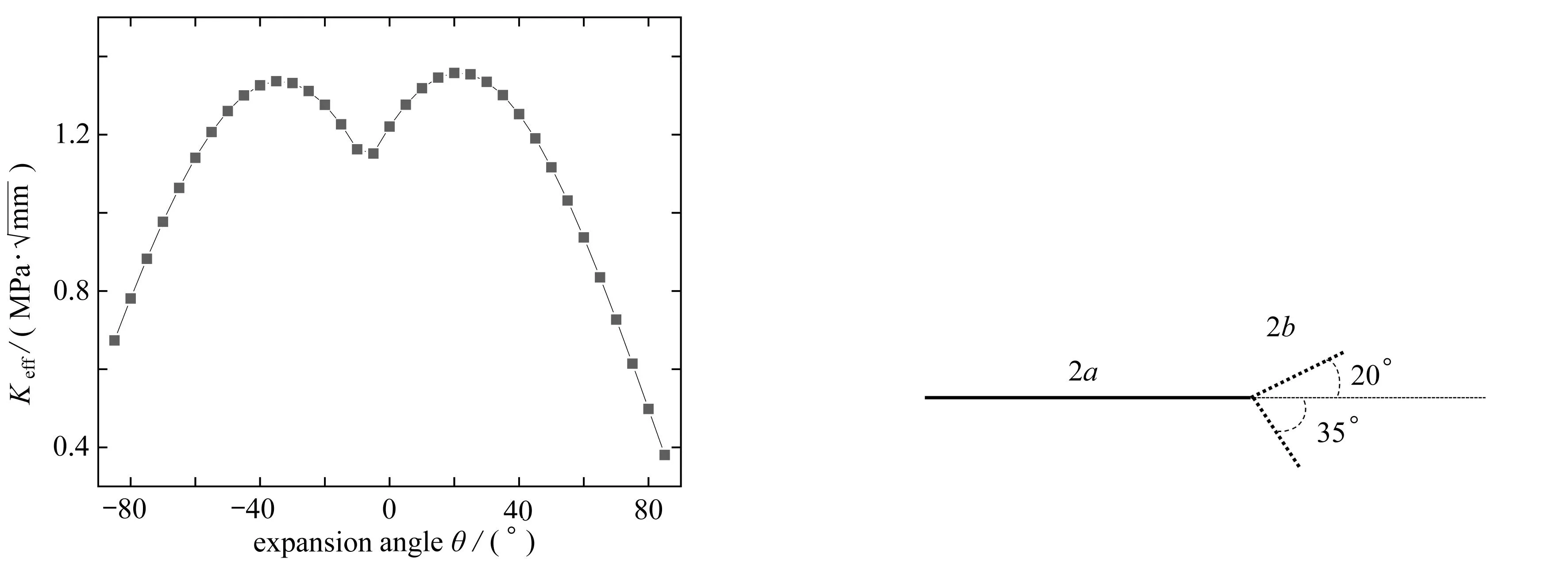
圖4 不同角度下的等效應力強度因子及裂紋分岔示意圖Fig. 4 Schematic diagram of the equivalent stress intensity factor and the crack bifurcation at different angles

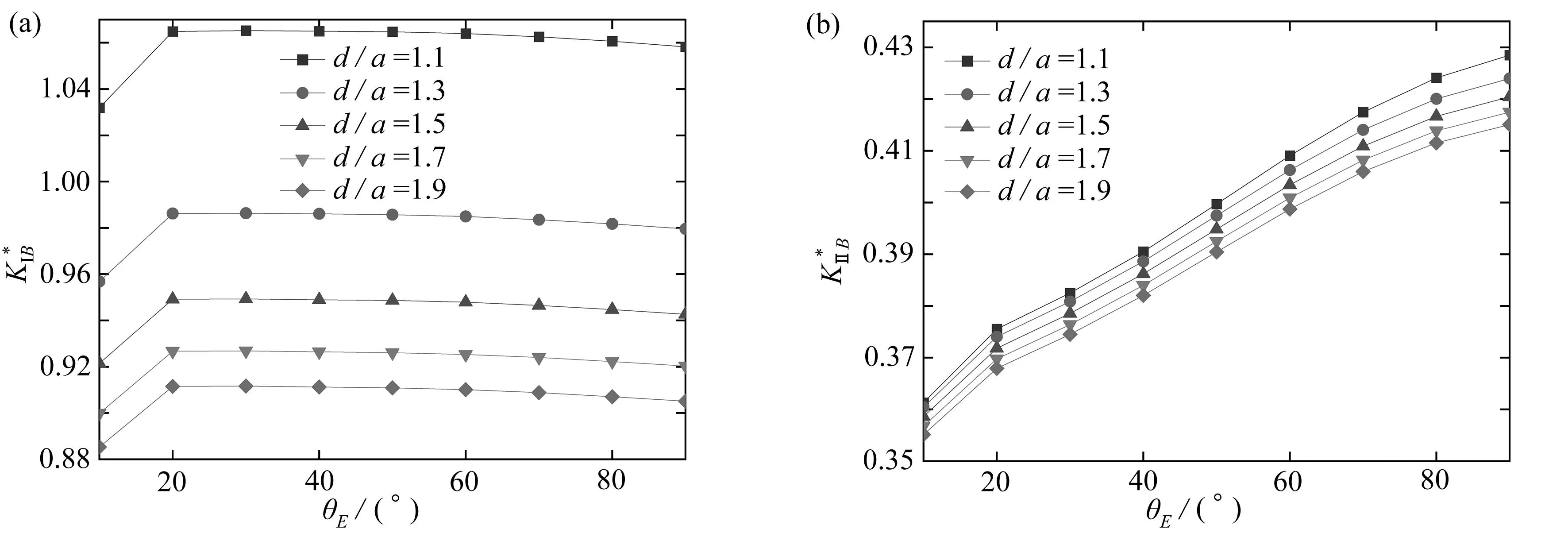
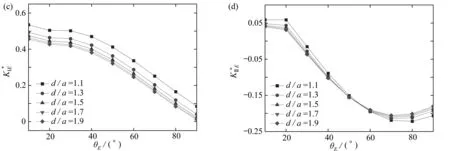
圖5 埋置深度對歸一化應力強度因子的影響Fig. 5 Effects of burial depths on normalized stress intensity factors

4.3 荷載比值τ/σ對和的影響

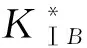
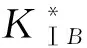
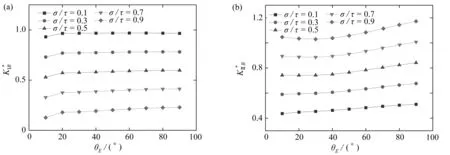
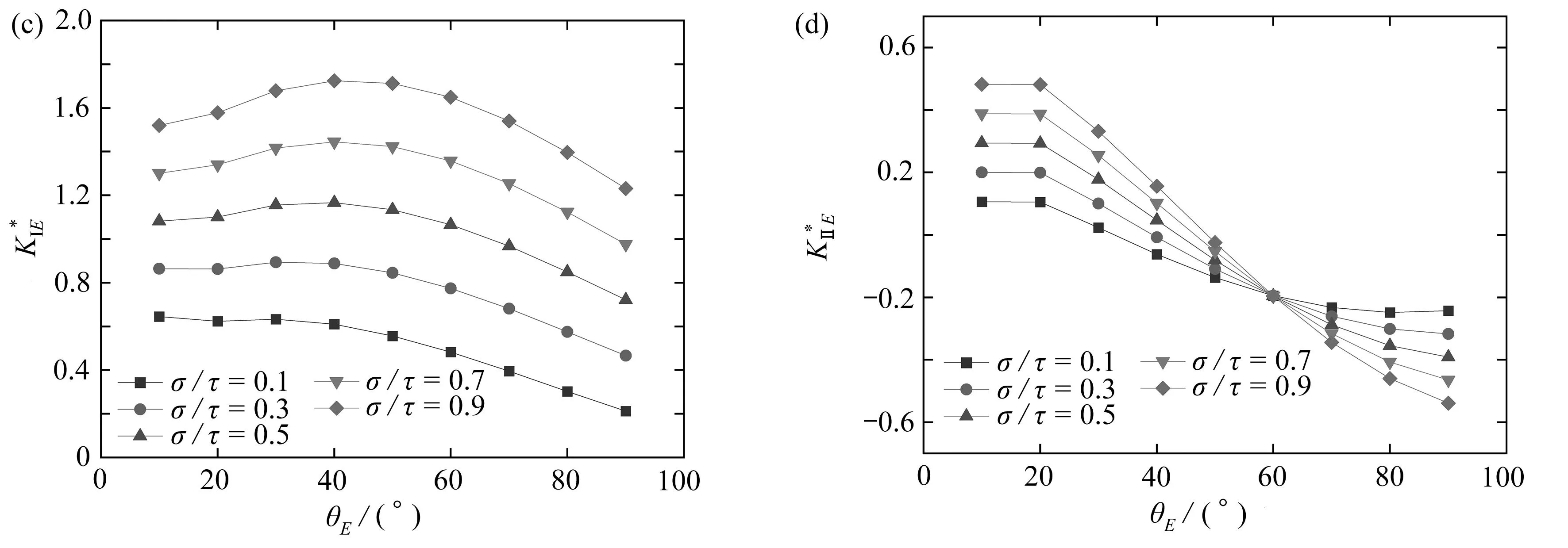
圖6 荷載比值對歸一化應力強度因子的影響Fig. 6 Effects of load ratios on normalized stress intensity factors

4.4 分支長度比值b/c對和的影響

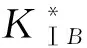
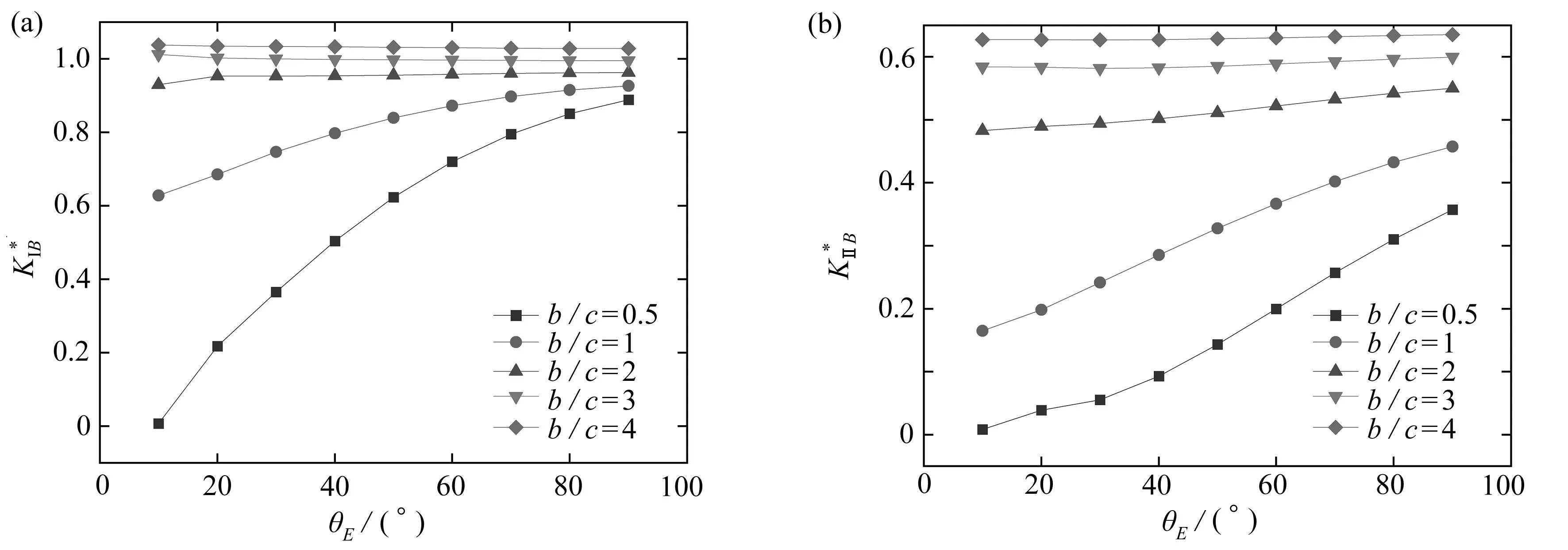
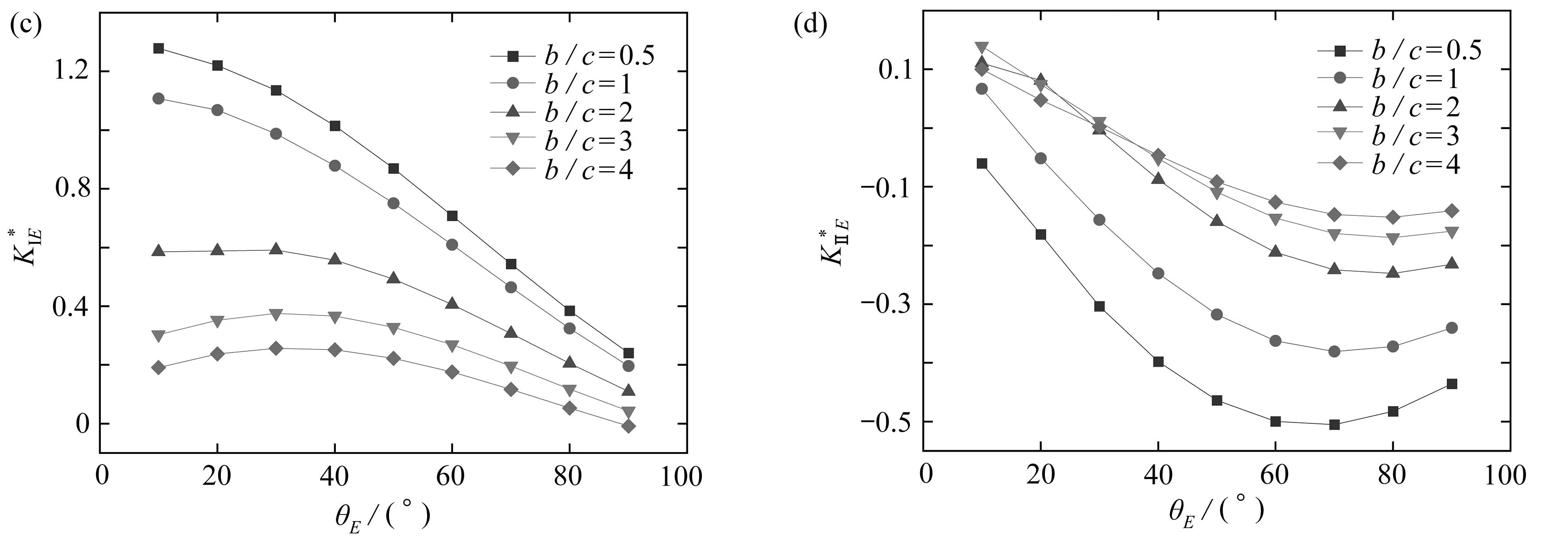
圖7 分支長度比值對歸一化應力強度因子的影響Fig. 7 Effects of branch length ratios on normalized stress intensity factors

4.5 分岔角度對和的影響

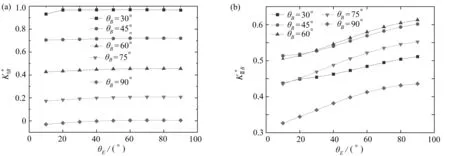
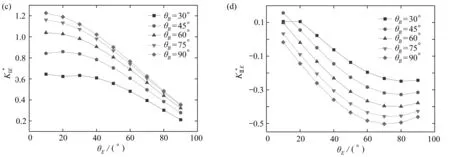
圖8 分岔角度對歸一化應力強度因子的影響Fig. 8 Effects of bifurcation angles on normalized stress intensity factors

4.6 多分支分岔裂紋的應力強度因子

本文所討論的理論方法可以方便地應用到多分支的分岔裂紋問題(圖9)中,相比較于以往解決的問題[15-17]更具工程價值,同時無需復雜的公式推導[18-19],只需要根據裂紋條數增加式(9)的個數,以及在分岔處根據式(11)進行相應的設置,便可以得到解答．令2a=4,2b=1,2c=0.5,θB=60°,θF=45°,將本文計算的結果與有限元進行比對,如表1所示．可見,本文給出的結果是可靠的,且相較于有限元計算而言,此方法可以方便快捷地用于解決多分支分岔裂紋問題,具有一定實際應用的價值．

圖9 多分支分岔裂紋示意圖以及有限元網格劃分局部圖Fig. 9 Schematic diagram of the multiple branch bifurcation crack and the local partial finite element mesh

表1 多分支分岔裂紋有限元計算與本文結果對照

5 結 論

1) 由上述推導過程及計算結果可知,本文研究分岔裂紋的方法可靠且便捷,可用于更加復雜的多分支分岔裂紋問題(如鹿角型分岔裂紋)．

2) 隨著埋入深度的增加,分岔裂紋兩分支的應力強度因子均逐漸減小,且裂紋長度越長對于埋深變化越敏感．當埋深達到d/a=1.5時,分支裂尖應力強度因子最大的削弱程度可達15%左右,這說明隨著埋深的增加,分岔裂紋向內部擴展會更加困難．

3) 分岔裂紋的分支長度越長,其應力強度因子越大,且長度較大的分支對長度較小的分支有一定的屏蔽作用,導致分岔裂紋更易向長分支方向擴展．在兩分支裂紋長度比達到b/c=2以上時,屏蔽效應可達50%以上．

4) 隨著荷載比值τ/σ的增加,當切應力大小與正應力大小相當時,分岔裂紋其中一分支的主導擴展模式由Ⅰ型擴展轉變為Ⅱ型擴展,另一分支的Ⅰ型應力強度因子峰值角度會增大．