基于IRT框架采用Angoff法進行合格標準設置的探索

楊觀惠 王曉慧

[摘要]學業水平考試分界分數的劃定關系到教育決策的科學性和公平性，涉及標準設定技術。為探究在項目反應理論（IRT）框架下采用Angoff法進行合格標準設置，以某地區初中學業水平考試某學科的模擬考數據為分析對象，將專家第三輪打分結果作為“最低合格能力考生”的作答數據，與真實考生的數據匯總，進行IRT參數估計。最終以“最低合格能力考生”能力分數的平均值-0.85作為合格的分界分數，該合格分數線的信息量為28.13，專家判斷與實際結果的Pearson相關系數為0.9，表明采用該方法進行標準設定具有較高的質量和推廣性。

[關鍵詞]標準設定；分界分數；合格分數線；Angoff法；學業水平考試；IRT

[中圖分類號]G424.74[文獻標識碼]A

[文章編號]1673—1654（2023）04—059—008

一、引言

隨著教育改革的深化，基礎教育階段各科目新版課標都明確了學業水平考試的學業質量水平，這為基于標準的教育考試提供了有利條件，使學業水平考試成為真正意義上的標準參照性測驗。在考試實踐中對分界分數的劃定鮮有體現基于標準的理念[1]，這會影響考試結果的效度。目前常用的百分比法劃定分界分數僅能提供學生在常模參照群體中的相對位置，無法提供說明學生知識、能力的信息[2]，考試結果僅能進行常模參照性解釋，科學性和公平性難以保證。這也無法反映學校對課程標準的執行情況，對教育教學的促進作用有限，使學業水平考試的評價反饋作用和教育監測功能受到限制[3]。關于考試合格水平的標準，我國傳統上用滿分的60%作為合格分數線（簡稱“60分法”），60分法由于簡單直觀在校本考試和部分大規模考試中運用廣泛。60分法是一種考前標準設置方法，在考試之前，文件規定了60分（含）以上為合格，60分以下為不合格。通過命題階段的質量控制技術[4]，使剛剛合格考生的平均分接近總分的60%。若命題階段沒有做好命題質量控制，則會影響考試效度，有的考試用60分法僅是沿襲這一習慣，實際并沒有與合格表現標準鏈接，沒有合理規劃試卷的難度結構，此時的60分就失去了意義，并不能代表達到合格水平。因此有些觀點認為60分法僅是形式上的一致[5-6]。

標準參照測驗的結果一般直接用于決策，如是否通過某項考核或能否獲得資格證，標準設置可為決策提供依據[7]。要科學地對學生進行分類決策，標準的設置應當具有科學的依據和可操作的方法，能夠被學界和社會同時認可與接受。探索合格標準設置方法有助于推動考試科學化，同時有利于促進學校認真執行課程標準，保障學業質量。

標準設置方法有很多，不同方法可能會產生不同的臨界分數，對考試結果的解釋也不同。在教育考試領域標準設置方法主要分為試題中心法和考生中心法[8]，前者是基于標準的判斷，后者是基于常模的判斷。試題中心法包括Angoff法及其變式、標簽法、Nedelsky法、Ebel法等；考生中心法包括臨界組法、對照組法等[9-10]。1971年提出的Angoff法是典型的試題中心法，也是最常用的標準設定方法，它的基本任務是界定各級別“最低能力考生”，對他們的表現標準達成共識，然后據此逐題判斷各級別最低能力考生的得分情況[11]。若要確定合格分數線，則需界定“最低合格能力考生”群體應達到的合格水平表現標準。在劃定分數的過程中將每一道試題與合格表現標準比對，若試題的能力要求低于或等于合格表現標準，那么“最低合格能力考生”應得分；若試題的能力要求高于合格表現標準，那么“最低合格能力考生”不得分。Angoff法的結果受專家的主觀性影響，一般需要多位專家對試題打分，至少經過3輪打分直到估計值比較穩定為止，以最后一輪的結果作為分界分數[12]。由此可見，Angoff法在標準設定過程中將表現標準轉化為試題的分界分數，實現與學業標準的連接，用該方法得到的分界分數可以有效地解釋學生的學業水平是否達到合格。該方法在最大程度上兼顧了科學性和可操作性，是國際上應用最廣泛的標準設定方法[13]，在我國主要運用于職業資格考試和大規模語言考試對標中[6-7，14-17]。

為貫徹基于標準的教育測量理念[2，18]，本文運用Angoff法和項目反應理論（IRT）將每道試題的能力要求與“最低合格能力考生”的能力水平進行對比判斷，探索一種與合格表現標準鏈接的標準設置方法。在命題完成后組織專家對試題進行打分，該方法將Angoff法第三輪打分結果作為“最低合格能力考生”的作答反應數據，在IRT框架下估計“最低合格能力考生”的能力分數，以平均值作為合格的分界分數θ0，并進行分界分數的信度分析[19-20]和一致性分析。在學業表現標準不變的情況下，不同年度的考試通過等值技術[1，14，21-23]可以使用相同的能力分數作為合格分界分數，實現不同年度合格標準的穩定性和可比性。

二、研究思路與方法

（一）研究思路

運用Angoff法需要專家根據相應的表現標準來判斷“最低合格能力考生”在每道試題上的作答表現。在判斷前，要確定該學科的水平標準。根據新版課程標準，學業質量標準是對學生學業成就表現的總體刻畫，是界定學科“最低合格能力考生”表現標準的依據。學科專家和評價專家運用賦分得分法判斷出“最低合格能力考生”在每道試題上的得分；在IRT框架下估計“最低合格能力考生”的能力分數，并計算該能力分數的信息量和信度作為分界分數的質量指標。為驗證標準設定的一致性，本研究對專家判斷和實測結果進行相關分析[16]。

（二）研究方法

目前，我國初中學業水平考試的功能定位是“兩考合一”“兼顧畢業和升學”，具有標準參照考試和常模參照考試的性質。單從升學角度看，標準設置獲得一個可信的合格分界分數顯得尤為重要。本研究以某地區初中學業水平考試某學科的模擬考數據為研究對象，采用改良Angoff法工作流程[23]組織7位專家判斷“最低合格能力考生”在每道試題上的得分情況。每輪打分結束后進行匯總，對差異較大的試題進行討論，再進行下一輪打分。以第3輪打分結果作為7位“最低合格能力考生”的作答反應數據，和真實考生的作答反應數據匯總在一起。使用R語言IRT分析工具，對該測驗的試題參數、考生能力分數（θ）（包括“最低合格能力考生”的θ）進行估計[24]，計算不同能力分數（θ）的信息量I（θ）、誤差Se（θ）和信度R（θ），并作圖反映該測驗的測量特征。以7位“最低合格能力考生”的能力分數的平均值作為合格的分界分數θ0，在信息量和信度圖中呈現及解釋合格分數線的位置及質量指標。一致性分析以分界分數上下一個測量誤差范圍的學生作為實際合格邊界考生[25]，計算專家判斷結果與實測結果的相關系數。

三、研究結果

（一）改良Angoff法賦分

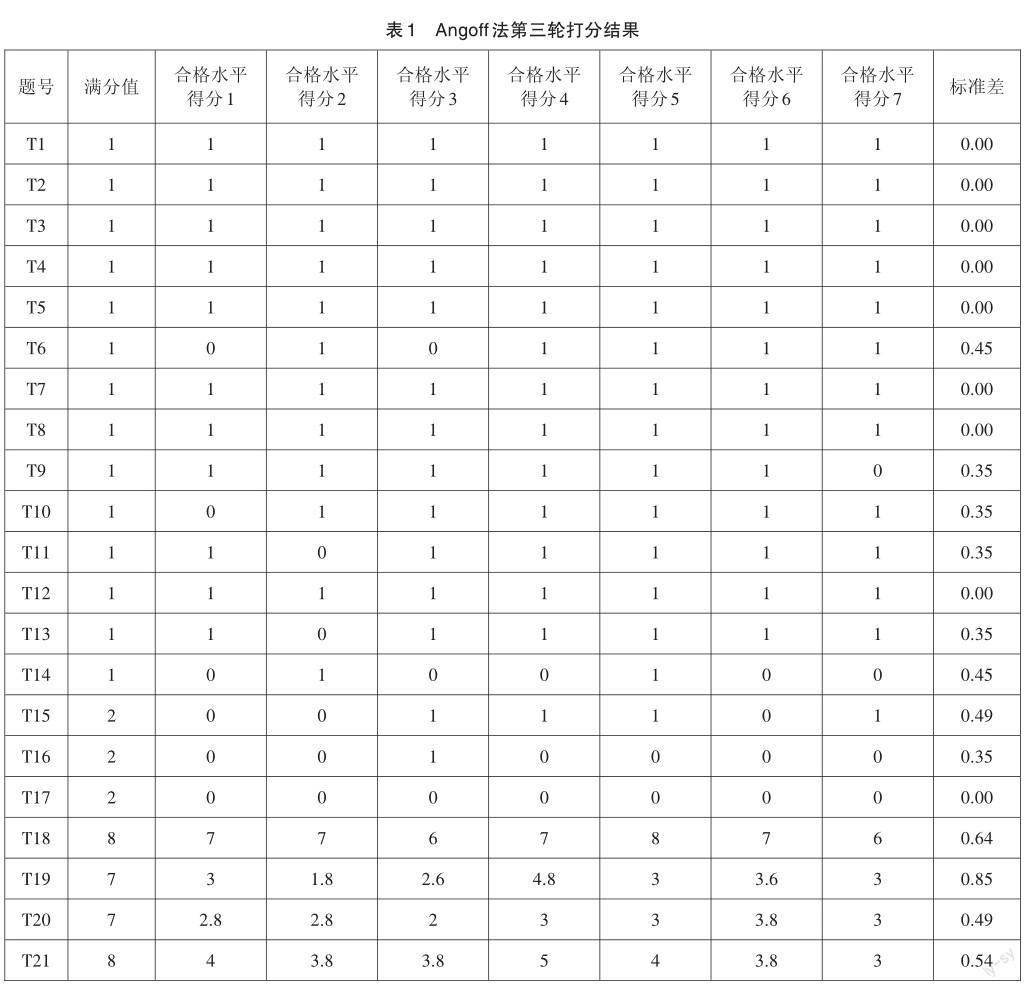
在改良Angoff法工作流程后，讓專家根據合格水平的表現標準在設計的打分表上采用賦分得分法[12]判斷“最低合格能力考生”在每個試題上的得分，例如某道試題滿分分值為3分，若認為“最低合格能力考生”能得2分，則賦2分。經過三輪打分后，結果趨向穩定。將7位專家第三輪打分的結果作為“最低合格能力考生”作答反應數據，如表1所示。從標準差數據可以看到，大部分試題專家判斷結果的內部一致性較高。

（二）項目反應理論分析

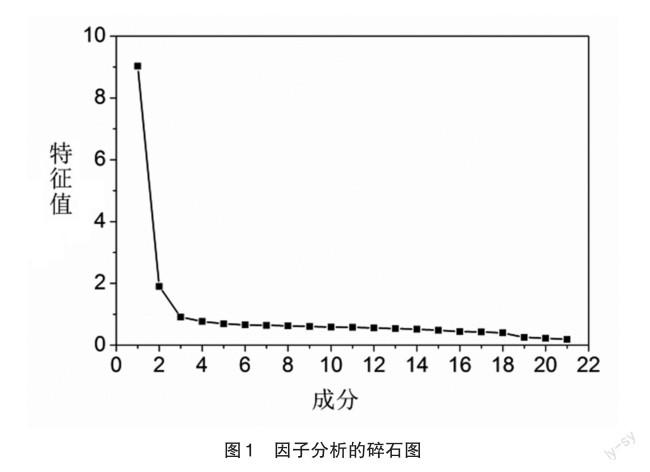
為確定測驗的維度，通過SPSS對測驗的各試題進行因子分析，碎石圖如圖1所示，第一特征值為 9.027，第二特征值為1.901，比值大于3，可以認為測驗符合單維性假設[26]。

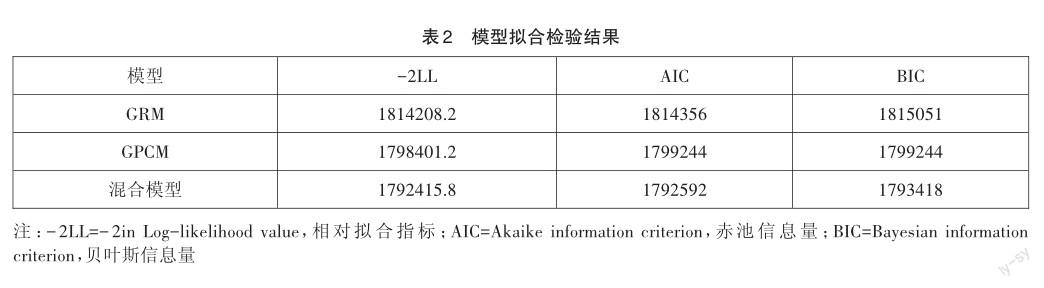
使用R語言對真實考生的應答數據進行模型擬合檢驗。測驗中前14道題為單選題，為0—1計分試題；T15-T17題為不定項選擇題，T18-T21題為簡答題，屬于多級計分試題。因此對該測驗分別檢驗了單維等級反應模型（簡稱“GRM”）、單維分部評分模型（簡稱“GPCM”）和單維混合模型[27]（前14題采用 logistic三參數模型，3道不定項選擇題采用GRM，4道簡答題采用GPCM）的擬合情況，結果如表2所示。根據相對擬合指標值越小擬合性越好的原則[28]可知，混合模型擬合效果更好，因此根據該模型進行后續分析。

對試題進行局部獨立性檢驗（Q3統計量）[24]，結果如表3所示，Q3統計量的值均小于0.36，可知所有試題滿足局部獨立的假設。

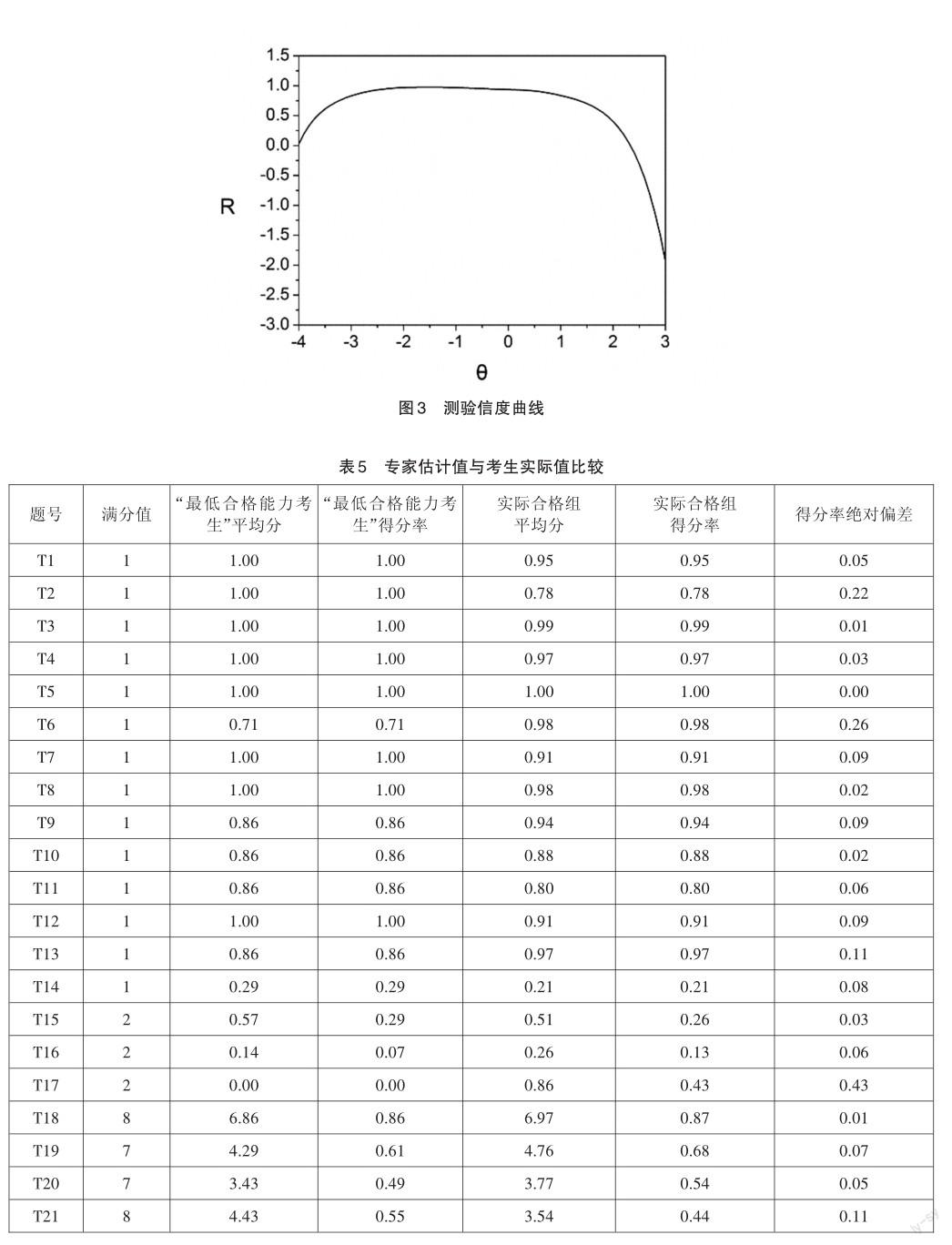
將7位“最低合格能力考生”作答反應數據和9895名真實考生的作答反應數據匯總在一起，共同作為本文的數據分析對象。IRT分析框架可以在同一量尺上估計試題的難度和學生的能力，使用R語言可得到試題的難度、區分度和猜測參數（單選題）的估計值以及每位考生能力θ的估計值。其中，7位“最低合格能力考生”的能力分數θ如表4所示，平均值為-0.85，以此作為合格的分界分數θ0。計算測驗信息量I（θ）、測量誤差Se（θ）和信度R（θ），并作圖反映該測驗的測量特征，測驗信息與誤差曲線如圖2所示，參考線對應的θ為-0.85，測量誤差為0.19；測驗信度曲線如圖3所示。

（三）一致性分析

為了檢驗改良Angoff法專家賦分結果的有效性，計算專家判斷與實測難度（得分率）的相關性，以此作為標準設定的一致性證據。將能力分數在分界分數上下一個測量誤差（-0.85±0.19）范圍內的被試看作實際合格邊界考生（簡稱“實際合格組”），統計專家判斷的“最低合格能力考生”和實際合格組在每道題上的平均分、得分率和得分率絕對偏差，如表5所示。偏差較大的試題為T2、T6和T17，其余試題的判斷絕對偏差在0.11以內。計算平均分與實際平均分（第3列與第5列）、得分率與實際得分率（第4列與第6列）的Pearson相關系數，分別為0.98和0.90，p值為0.000（顯著相關），說明專家判斷與實測結果高度一致。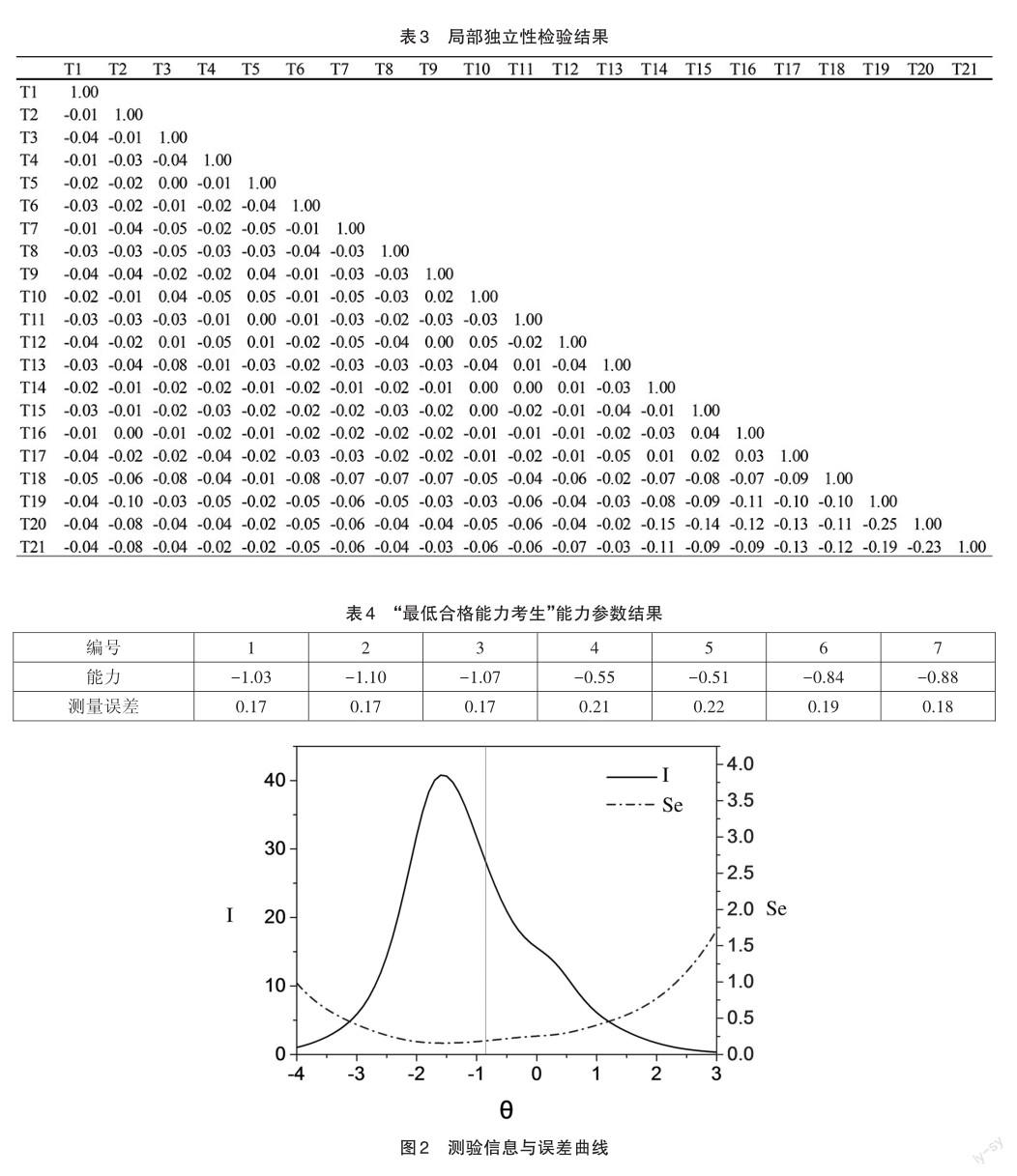

四、討論

項目反應理論中，信息量反映測驗的質量：信息量越大，對被試能力估計的誤差越小。對于標準參照測驗，應在分界分數及其附近有精確的估計和高區分的能力，信息量大于25表明測驗質量理想[19]，因此可將分界分數點的信息量作為標準標定的質量指標。由圖2可知，分界分數θ0的信息量I（-0.85）= 28.13，信度R（-0.85）=1-1/I=0.96，表明該分界分數具有較高的測量精度和區分能力，采用該方法進行標準設定的質量較好。在表現標準不變的情況下，不同年份的考試通過等值技術可采用相同的能力分數作為合格的分界分數，具有穩定性和可比性，容易被社會接受。

目前，基礎教育階段新版課程標準中都明確了各學科學業質量標準，為基于標準的教育與評價提供了有利條件。考試機構可以依據學業質量水平開發標桿卷，依據科學的標準設定方法劃定分界分數，在每年的測驗編制中做好等值設計，再通過等值處理將測驗的分數轉化為標桿卷的能力分數，由此可依據標桿卷的分界分數進行分類，避免頻繁進行標準設定。

該合格標準設置方法目前僅使用模擬考數據進行了檢驗，尚未推廣。一是Angoff法工作流程比較復雜；二是在分數解釋時，需要有一定的測量基礎才能夠理解。因此，若在實際中進行推廣，需要對利益相關者進行深入的科普和宣講，并且需要教育行政部門的支持和廣泛的社會認同。

學業水平考試分界分數的劃定關系到教育決策的公平性和科學性，分界分數應具有較高的信度。本研究通過Angoff法工作流程組織專家界定“最低合格能力考生”并逐題判斷他們在每道題上的得分，以此作為“最低合格能力考生”的作答反應數據，將這些數據和真實考生的作答反應數據匯總在一起，在IRT框架下進行參數估計。從能力參數估計的結果獲得“最低合格能力考生”的能力分數θ，以平均值-0.85作為合格的分界分數，對應的信息量為28.13，表明分界分數具有較高的信度。專家估計值與實測值的相關分析表明專家判斷與實際結果一致性較高，因此采用該方法進行標準設定的質量較好。該方法可推廣至多個等級分界分數的劃定或其他標準參照性考試。此外，通過等值技術可實現不同年度合格標準的穩定性，避免頻繁設定合格標準。

參考文獻：

[1]羅瑩，韓思思.高考改革選考科目等級評定標準研究[J].教育科學研究，2018，（06）：11-14.

[2] Tognolini Jim，Stanley Gordon，杜承達.基于標準的評核：教育領域人力資本和能力提升的工具與方法[J].考試研究，2010，6（02）：4-20.

[3]宋寶和，趙雪.高中學業水平合格性考試的設計及價值分析[J].中國考試，2019，（01）：19-23.

[4]王曉華.基于標準的教育考試合格標準研究[J].教育科學，2012，28（05）：15-21.

[5]趙世明.科學確定專業人才資格考試的合格標準[J].中國人才，2007，（17）：66-67.

[6]景匯泉，郭永松，孫寶志，等.考試合格標準設置的國內外現狀[J].中國高等醫學教育，2007，（10）：56-57.

[7]汪存友.科學設定職業資格考試合格標準[J].中國考試，2012，（04）：43-47.

[8]余嘉元. Angoff方法有效性的檢驗研究[J].教育研究與實驗， 2008，（01）：54-57.

[9]李珍，辛濤，陳平.標準設定：步驟、方法與評價指標[J].考試研究，2010，6（02）：83-95.

[10]向冠春.標準設定與等級劃分[J].成人教育，2013，33（01）：14-20.

[11]閔尚超.接受型語言考試與語言標準對接的效度問題——一致性[J].現代外語，2019，42（05）：696-708.

[12]范士娟，王曉慧.上海市普通高中信息科技學業水平合格性考試合格標準劃分初探[J].考試研究，2020，（03）：47-52.

[13]汪存友.ETS iSkills～（TM）測驗的標準設定及其對NTET的啟示[J].電化教育研究，2012，33（02）：59-64.

[14]汪存友.關于設定全國中小學教師教育技術水平考試合格標準的思考[J].中國遠程教育，2013，（03）：49-53.

[15]閔尚超，姜子蕓.校本聽力考試與《中國英語能力等級量表》對接研究[J].外語教學，2020，41（04）：47-51.

[16]張潔，王偉強.接受型語言考試與語言標準對接的效度問題——來自標準設定過程的證據[J].現代外語，2019，42（05）：684-695.

[17]何懼，何佳，安滔，等. Angoff法及其衍生方法在資格考試合格線設定中的比較研究[J].中國考試（研究版），2007，（06）：23-26.

[18]雷新勇.學業標準——基于標準的教育改革必須補上的一環[J].上海教育科研，2009，（06）：15-18.

[19]溫紅博，卜文娟，劉先偉.初中學業水平考試中固定比例法標準設定的信度分析[J].考試研究，2017，（05）：55-63.

[20]江西師大現代教育和心理測量通用分析系統研制組，漆書青，周駿，等.用信息函數法對標準參照測驗作質量分析[J].心理與行為研究，2003，（01）：34-39.

[21]楊志明.學業水平考試事后等值的概念、條件與設計[J].教育測量與評價，2016，（11）：4-8.

[22]楊志明.做好高中學業水平考試所必須的四項測量學準備[J].中國考試，2017，（01）：8-13.

[23]楊志明.高中學業水平考試等級設定的若干方法[J].教育測量與評價，2016，（10）：4-9.

[24]羅照盛.項目反應理論基礎[M].北京師范大學出版社，2012.

[25]汪存友，余嘉元，張穎.調和Angoff法在設定執業醫師資格考試分數線中的應用[J].中國考試，2011，（10）：38-43.

[26] Slocum S L. Assessing Unidimensionality of Psychological Scales：Using Individual and Integrative Criteria from Factor Analysis[D]. University of British Columbia，2005.

[27]涂冬波，蔡艷，戴海琦，等.項目反應理論新進展：基于3PLM和GRM的混合模型[J].心理科學，2011，34（05）：1189-1194.

[28]單昕彤，譚輝曄，劉永，等.項目反應理論中模型——資料擬合檢驗常用統計量[J].心理科學進展，2014，22（08）：1350-1362.

Exploration of Qualified Standard Setting with Angoff Method Based on IRT Framework

Yang Guanhui Wang Xiaohui

Shanghai Municipal Educational Examinations Authority，Shanghai，200433

Abstract：Setting cut-off scores for the academic proficiency test is related to the scientificity and fairness of the educational decision-making，which involves standard setting techniques. This study explored the adoption of Angoff method for the qualified standard setting according to Item Response Theory（IRT），taking the mock test data of a subject in the junior high school proficiency test in a certain area as an example.The experts third round scoring results were used as the response data of the "minimum qualified candidates"，and the data of real candidates were put together for parameter estimation by R. The average of the ability score of the "minimum qualified candidates" is -0.85. Taking it as the qualified cut score，the information content of this point is 28.13. Additionally，the Pearson correlation coefficient between expert judgment and actual result was 0.9. The results showed that this method had high quality in standard setting.

Key words：Standard Setting，Cut Score，Passing Score，Angoff Method，Academic Proficiency Test，IRT

（責任編輯：吳茳）