鐵路自復位橋墩地震動最不利輸入方向研究

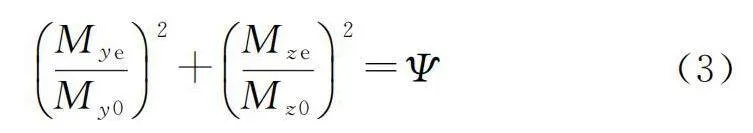
摘要： 為探究地震動輸入角度對鐵路自復位橋墩地震反應的影響，以一座簡支梁橋為工程背景，建立空間自復位橋墩地震反應分析模型，并對模型進行驗證。選擇22組強震記錄作為地震動輸入，以屈服面函數Ψ作為判別最不利輸入角度的標準，從0°開始順時針旋轉，每次增加5°，進行鐵路自復位橋墩地震反應分析。結果表明：145°輸入時，Ψ值最大，145°為橋墩最不利輸入角度;在最不利方向下橋墩的地震反應大于順橋向和橫橋向。自復位橋墩設計時若不考慮地震動最不利輸入方向，則偏于不安全。

關鍵詞： 自復位橋墩; 三維地震動; 最不利角度; 屈服面函數

中圖分類號： U442.59 文獻標志碼：A 文章編號： 1000-0844（2024）06-1380-07

DOI：10.20000/j.1000-0844.20230706001

Critical angle of earthquake input for self-centering

bridge piers of railways

ZHU Haoran¹， XIA Xiushen¹， ZHONG Yawei²， DAI Shengyong²

（1. Lanzhou Jiaotong University， Lanzhou 730070， Gansu， China;

2. China Railway Eryuan Engineering Group Co.， Ltd.， Chengdu 610031， Sichuan， China）

Abstract： To investigate the influence of ground motion input angles on the seismic response of railway self-centering piers， a seismic response analysis model for spatial self-centering bridge piers was established and validated using a simply supported beam bridge as the case study. A total of 22 sets of strong motion records were selected as seismic inputs. The yield surface function Ψ was used to determine the critical input angle. Starting from an initial angle of 0°， the seismic response of the railway self-resetting pier was examined by rotating clockwise， increasing the angle by 5° increments each time. The results show that the value of Ψ was maximized at an input angle of 145°， designating this as the critical input angle for the pier. The seismic response in this critical direction surpassed those observed in the longitudinal and transverse directions. Designs that ignore the critical angle of ground motion in the design of self-centering bridge piers may be unsafe.

Keywords： self-centering pier;three-dimensional ground motion;critical angle;yield surface function

0 引言

由于地震動的空間性和不確定性，不同的地震動輸入方向會引起結構不同的地震反應。普通橋梁結構只需考慮水平向地震作用，按順橋向或橫橋向分別輸入地震動，即可得到最不利地震反應^［1］。而地震動輸入方向對復雜結構的影響則需要進一步研究。Torbol等 ^［2］研究表明不考慮地震動的入射角會明顯低估橋梁結構的地震反應。單德山等^［3］利用增量動力分析方法探究了薄壁橋墩的最不利輸入角度，發現橋墩的地震反應和地震動入射角有關。李小珍等^［4］以某鐵路部分斜拉橋為研究對象，提出在進行地震反應分析時，應考慮豎向地震動及水平地震動最不利輸入方向的影響。韓恩圳等^［5］研究發現，對于豎向振型為主的結構，應考慮多維地震動輸入并計算出結構的最不利角度。王滔等^［6］研究發現，橋墩的最不利方向與結構自身特性和輸入的地震波有關。國內外學者對最不利方向的研究方法主要基于能量法和反應譜法。Lpez等^［7］提出了利用反應譜形狀來確定最不利入射方向的方法。馮云田等^［8］引入結構抗震主軸的概念，利用結構最大變形來確定地震動的最不利輸入方向。范立礎等^［9］利用輸入能量和屈服面函數的方法研究了復雜結構地震動輸入最不利方向的標準。

Housner等^［10］在20世紀60年代提出搖擺隔震的概念，其可以作為一種有效的隔震方法。司炳君等^［11］、孫治國等^［12］和鐘正午等^［13］通過試驗與模擬相結合，驗證了搖擺自復位橋墩擁有較好的抗震性能。Palermo等^［14-16］、Solberg等^［17］和Ou等^［18］提出了一種采用無黏結預應力技術并內置耗能鋼筋的新型搖擺橋墩設計，通過擬靜力和擬動力試驗驗證了這種新型搖擺橋墩具有較好的自復位能力，可以顯著減小橋墩損傷。夏修身等^［19-20］提出中等高度鐵路橋墩可以采用自由搖擺的方法隔震，并通過試驗證明了隔震搖擺橋墩具有自復位能力。鐵路自復位橋墩的墩柱截面多是圓端形，這種截面的縱、橫向尺寸相差大，各個方向的慣性矩不同，在地震力作用下的抗側承載力和耗能能力也不同，因此，圓端形截面各個方向的抗震能力是有差異的。當地震動沿著斜向方向作用時，很難判定橋墩是否被破壞，再加上橋墩的提離搖擺與輸入方向有關，因此，探究鐵路自復位橋墩的最不利輸入方向是有必要的。

本文以一座鐵路簡支梁橋為工程背景，建立空間自復位橋墩地震反應分析模型，并對模型進行驗證;選擇22組近斷層地震動記錄作為地震動輸入，以屈服面函數作為判別最不利輸入角度的方法，從0°方向開始順時針旋轉，每次增加5°，對鐵路自復位橋墩的地震反應進行分析，探討其最不利輸入方向。

1 模型的建立與驗證

1.1 工程背景

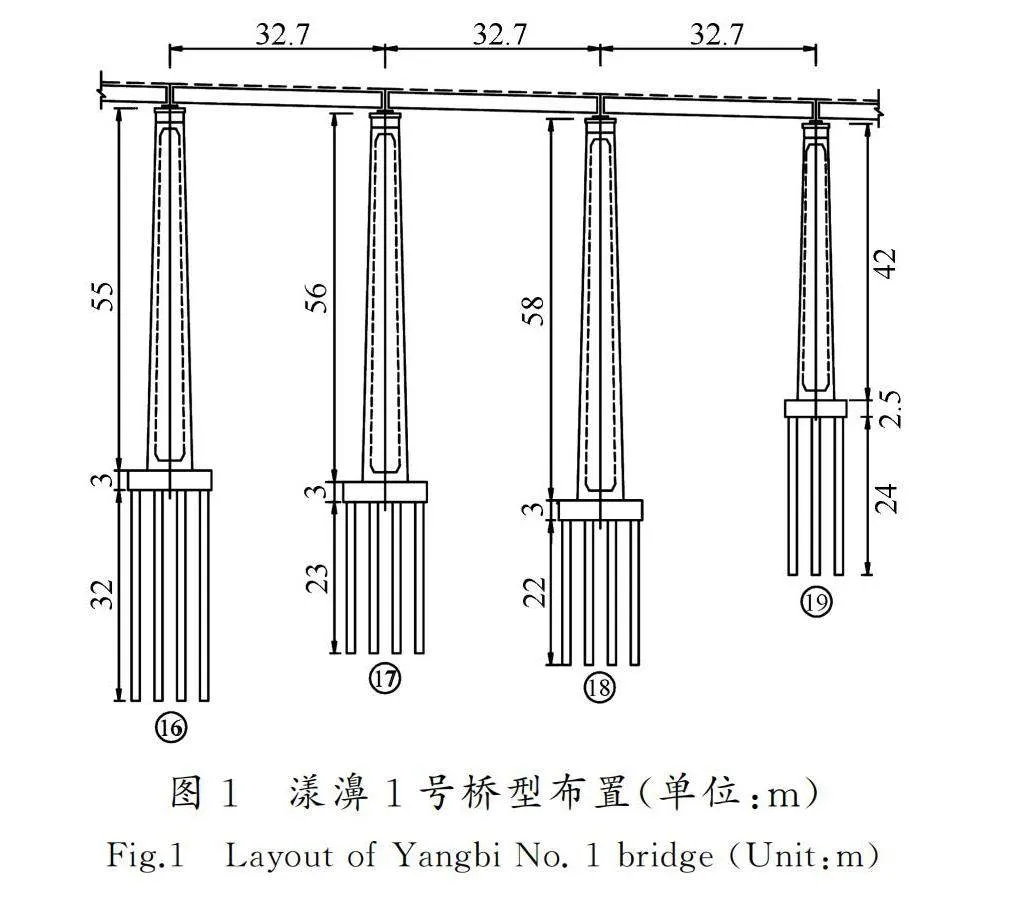
本文以云南省大理至瑞麗線漾濞1號特大橋18號橋墩為工程背景（圖1）。上部結構為等跨簡支箱形梁，跨度32.7 m;下部結構為圓端形空心高墩，墩高58 m，墩底截面尺寸為7 m（順橋向）×9.1 m（橫橋向）×1.12 m（壁厚）。對傳統的18號橋墩進行再設計，使其成為自復位橋墩。再設計后的墩底擴大基礎為C30混凝土，寬B=10 m，截面面積A₀=120 m²，全截面縱向配筋率及配箍率均為0.7%。自復位橋墩的設計過程及詳細設計參數見文獻［21］。

1.2 模型建立

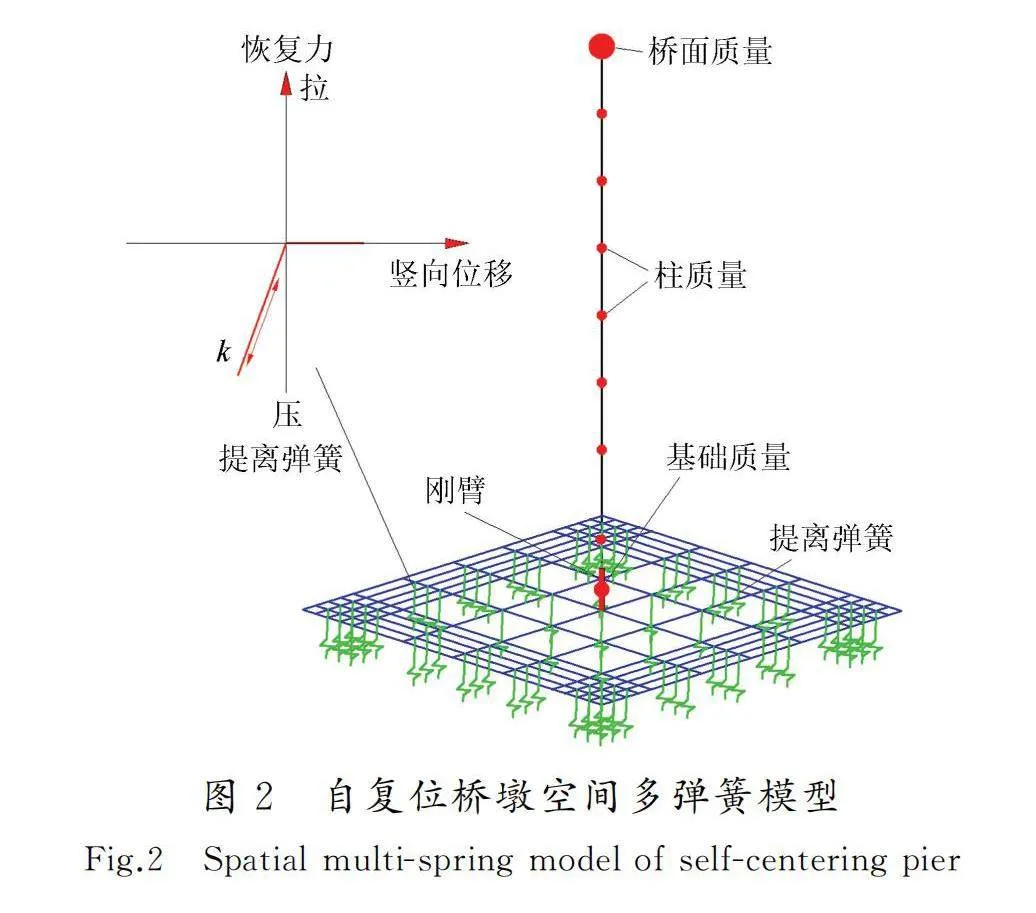
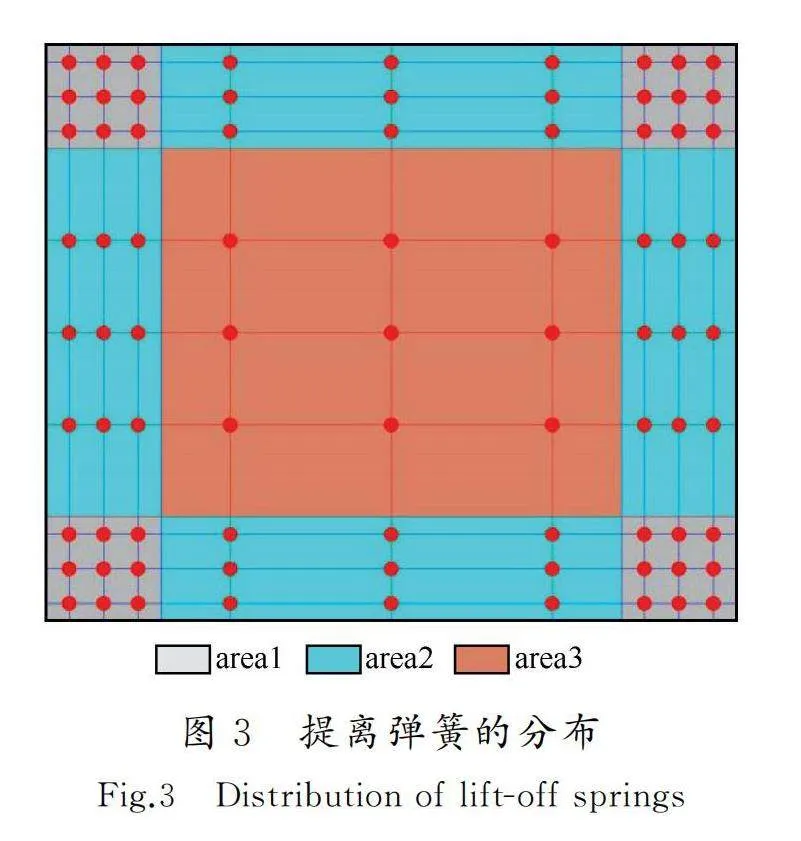
采用81個豎向只受壓不受拉彈簧模型來模擬三維地震動下自復位橋墩的提離搖擺，基于MIDAS/Civil分析軟件建立自復位橋墩空間多彈簧模型（圖2）^［21］。模型橋墩由360個節點和430個單元組成，墩身由梁單元模擬，承臺和擴大基礎由剛臂單元模擬。利用集中質量模擬橋跨重量，在第27和第230個節點處施加靜力荷載，擴大基礎的質量集中于重心。基礎兩端area1、area2區各布置36根彈簧，基礎中部area3區布置9根彈簧。只受壓彈簧的模型和力-位移關系如圖2所示。參考文獻［22］，空間多彈簧分布如圖3所示，提離彈簧的豎向剛度按式（1）、（2）計算（表1）。

k_area1amp;2=6.83G/1-ν （1）

k_area3=0.73G/1-ν （2）

式中：k_area1amp;2為基礎area1區和area2區每平方米的彈簧剛度;k_area3為基礎area3區每平方米的彈簧剛度;G為基礎材料的剪切模量;ν為基礎材料的泊松比。

1.3 模型驗證

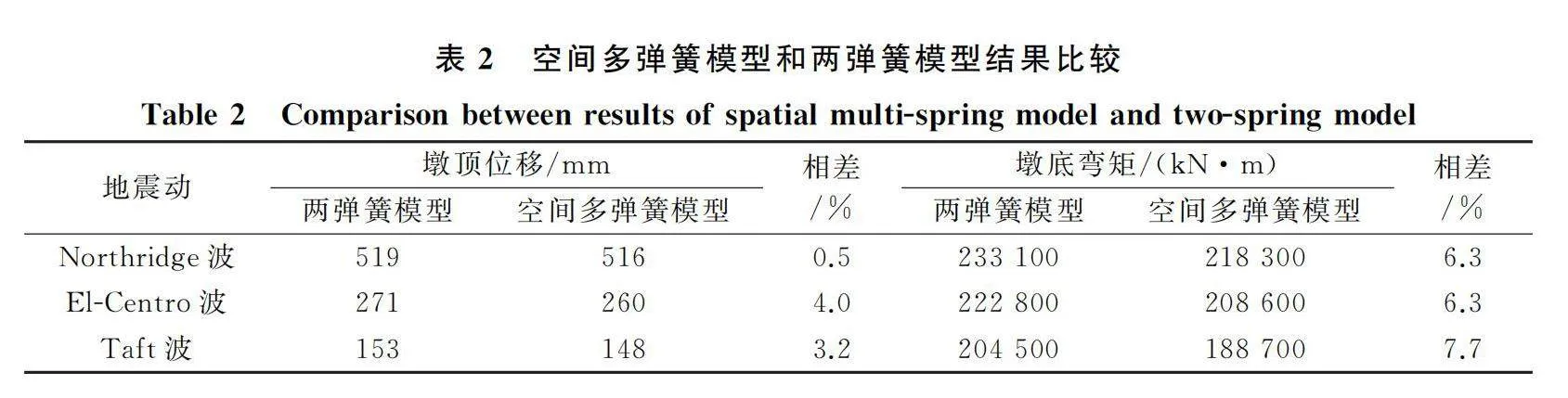
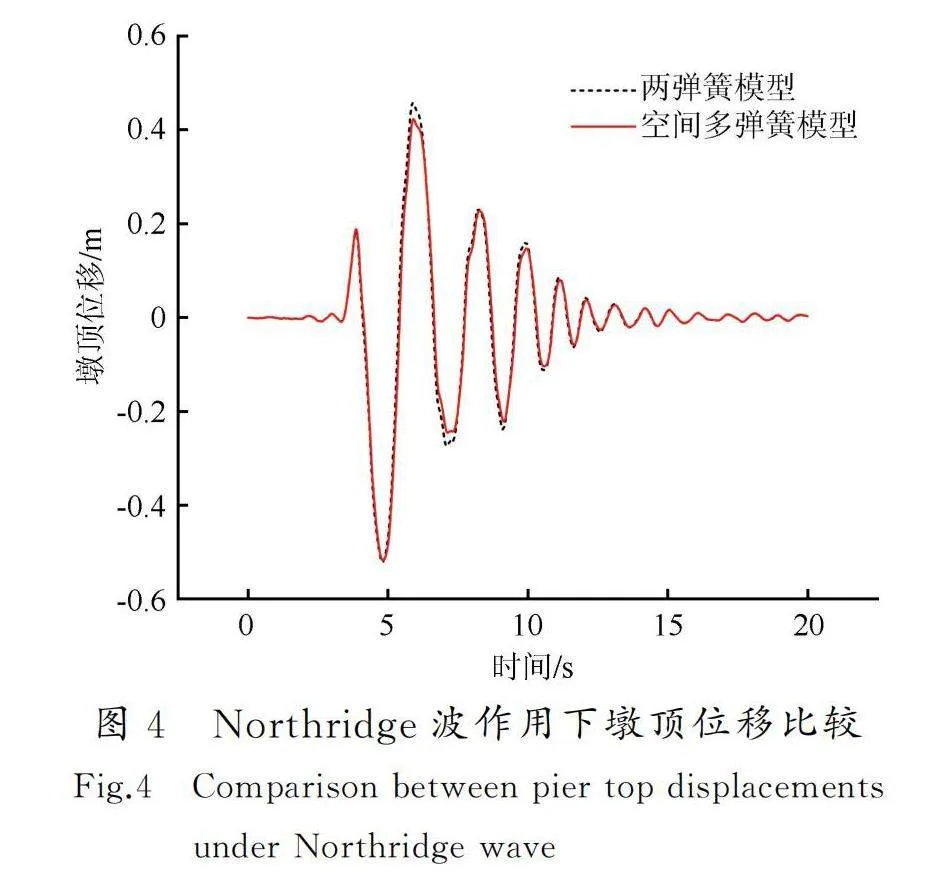
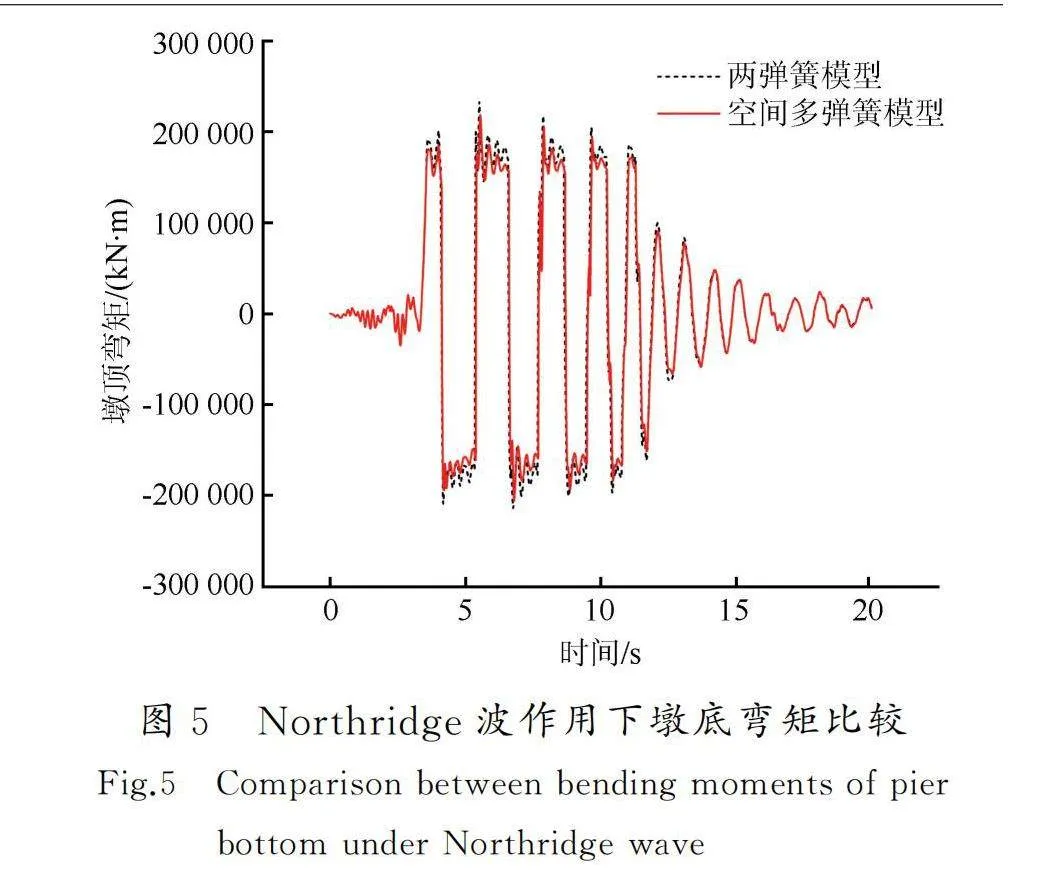
夏修身等^［22-23］針對鐵路自復位橋墩提出了一種簡化的兩彈簧模型，并通過振動臺試驗驗證了用兩彈簧模型模擬自復位橋墩提離搖擺的合理性。在文獻［24-25］中，兩彈簧模型通過OpenSees平臺，可以在地震動作用下較好地模擬自復位橋墩的地震反應，因此，本文利用其對鐵路自復位橋墩空間多彈簧模型進行驗證。選取Northridge波、El-Centro波、Taft波三條強震記錄，將地面峰值加速度（Peak Ground Acceleration，PGA）統一調整為0.57g。兩彈簧模型和空間多彈簧模型在三種地震波輸入下的墩頂位移和墩底彎矩的對比列于表2，在Northridge波作用下墩頂位移和墩底彎矩的比較分別如圖4、5所示。

通過表2可以看出，兩個模型的墩頂位移在Northridge波下相差最小（0.5%），在El-Centro波下相差4.0%;墩底彎矩在Northridge波、El-Centro波下相差6.3%，在Taft波下相差最大（7.7%）。通過圖4、5可以看出，在Northridge波下兩個模型的墩頂位移和墩底彎矩時程曲線吻合較好。由此可知，空間多彈簧模型可以較好地模擬自復位橋墩的地震反應。

2 地震波選取

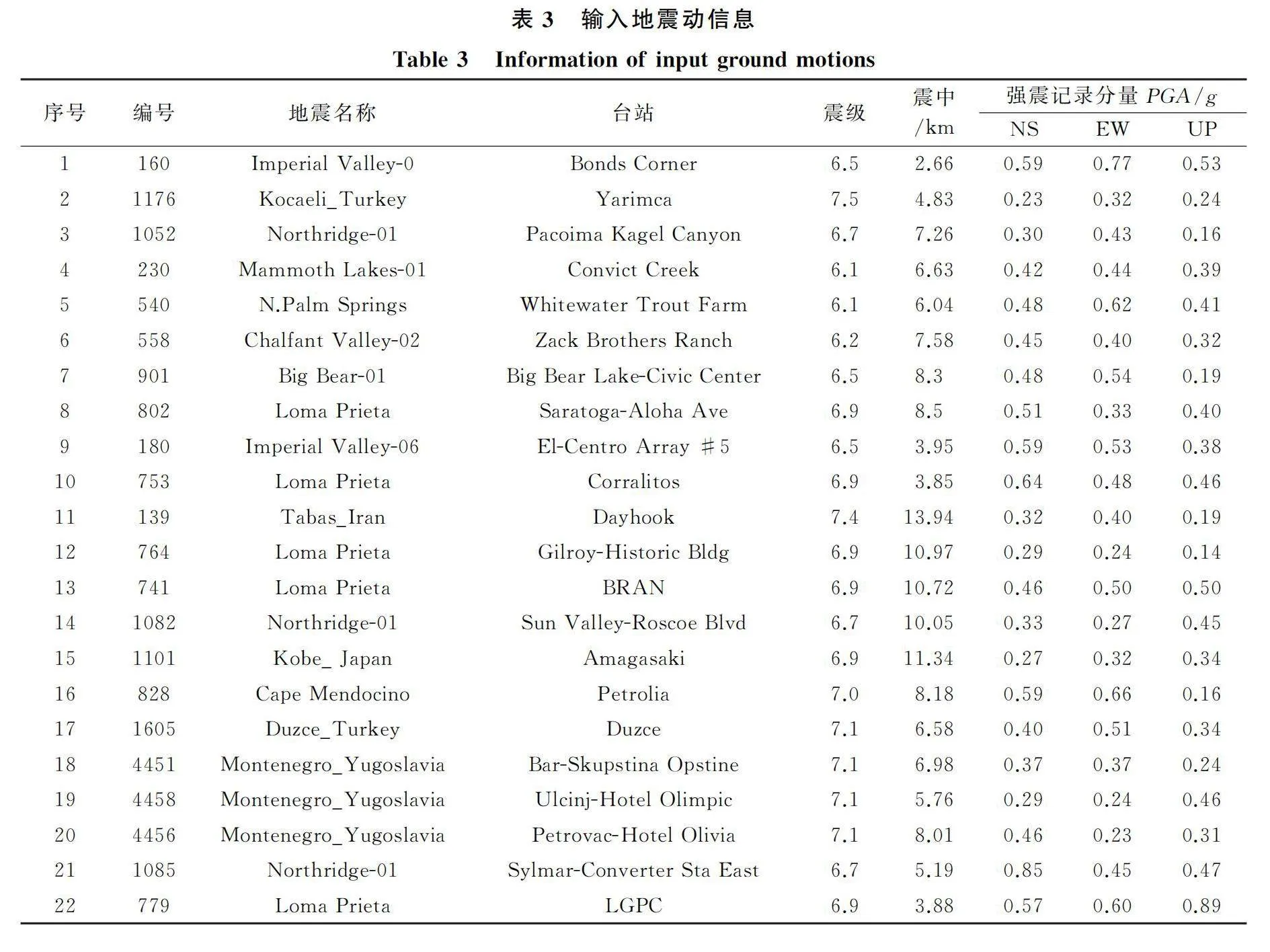
根據Vamvatsikos等^［26］的研究，20組地震工況即可反映地震動的不確定性。將震中距2～15 km，地面峰值速度（Peak Ground Velocity，PGV）＞10 cm/s，PGA＞0.2g，PGV/PGA較大，速度脈沖的持時不得小于0.5 s作為選取近斷層地震波的條件，從美國太平洋強震數據庫（Pacific Earthquake Engineering Research Center，PEER）中選取22組近斷層地震波。每組地震波包括兩個水平分量（NS，EW）和1個垂直分量（UP）。

3 算例分析

以1.1節的背景橋墩作為研究對象，采用1.3節中經過驗證的空間多彈簧模型，進行地震動最不利輸入角度分析。以表3中22組近斷層地震波為三向輸入，在0°～180°中，兩個水平方向的地震動沿順時針輸入，每次輸入角度間隔為5°。

3.1 最不利輸入角度的評判方法

自復位橋墩在三向地震動輸入下會產生兩個方向的彎矩，即順橋向彎矩M_ye和橫橋向彎矩M_ze。兩個方向的彎矩相互影響，任何單一方向地震動輸入所達到的最大彎矩不能作為判別截面最不利方向的標準。為了研究自復位橋墩在三維地震動下的最不利方向，采用Bresler等^［27］和孟杰等^［28］給出的屈服面函數Ψ［式（3）］作為最不利輸入方向判定標準。當Ψlt;1時，橋墩處于線彈性狀態;當Ψ≥1時，橋墩則達到屈服狀態。

M_ye/M_y0²+M_ze/M_z0²=Ψ （3）

式中：M_y0為墩底順橋向初始屈服彎矩;M_z0為墩底橫橋向初始屈服彎矩。

3.2 地震動最不利輸入角度分析

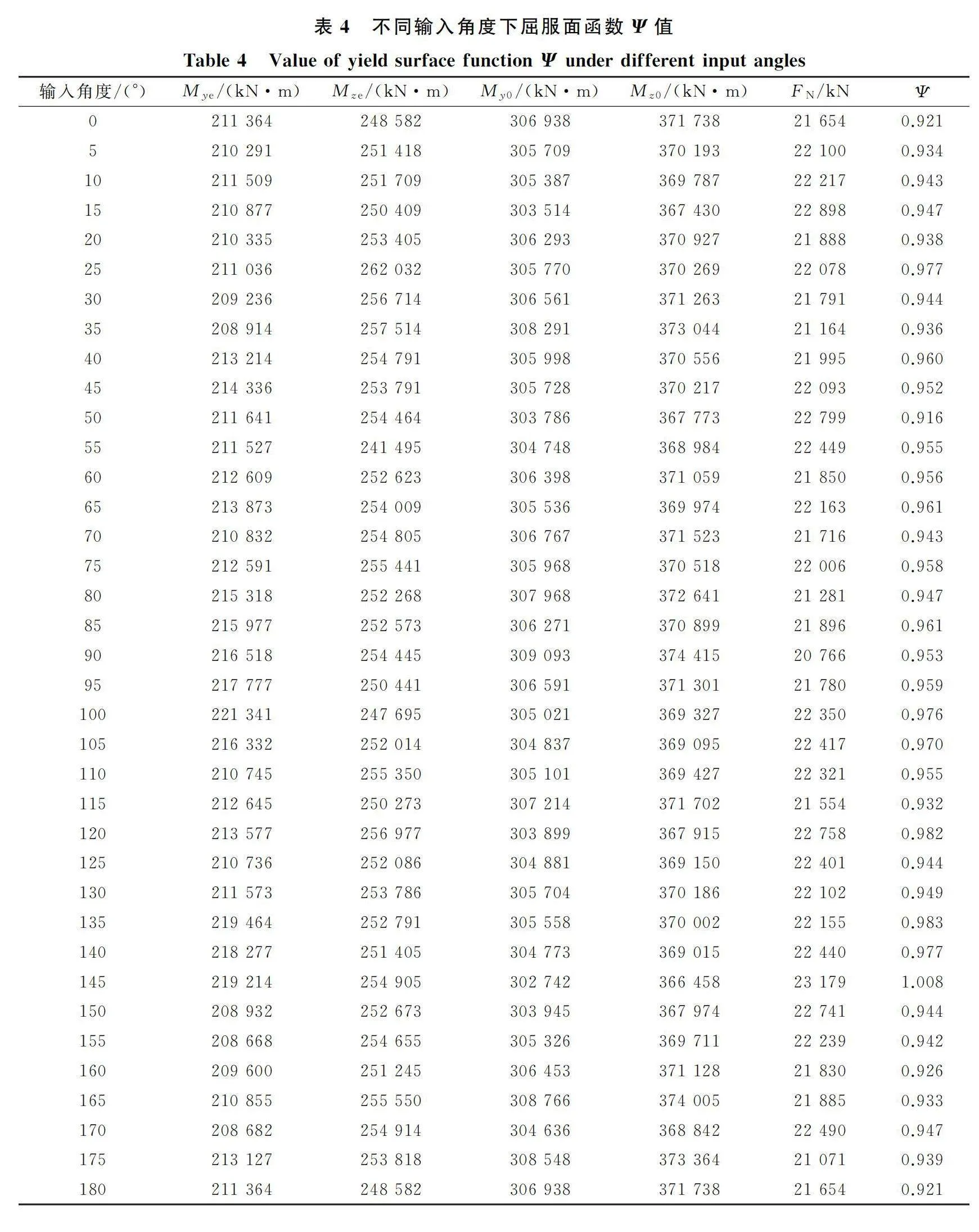
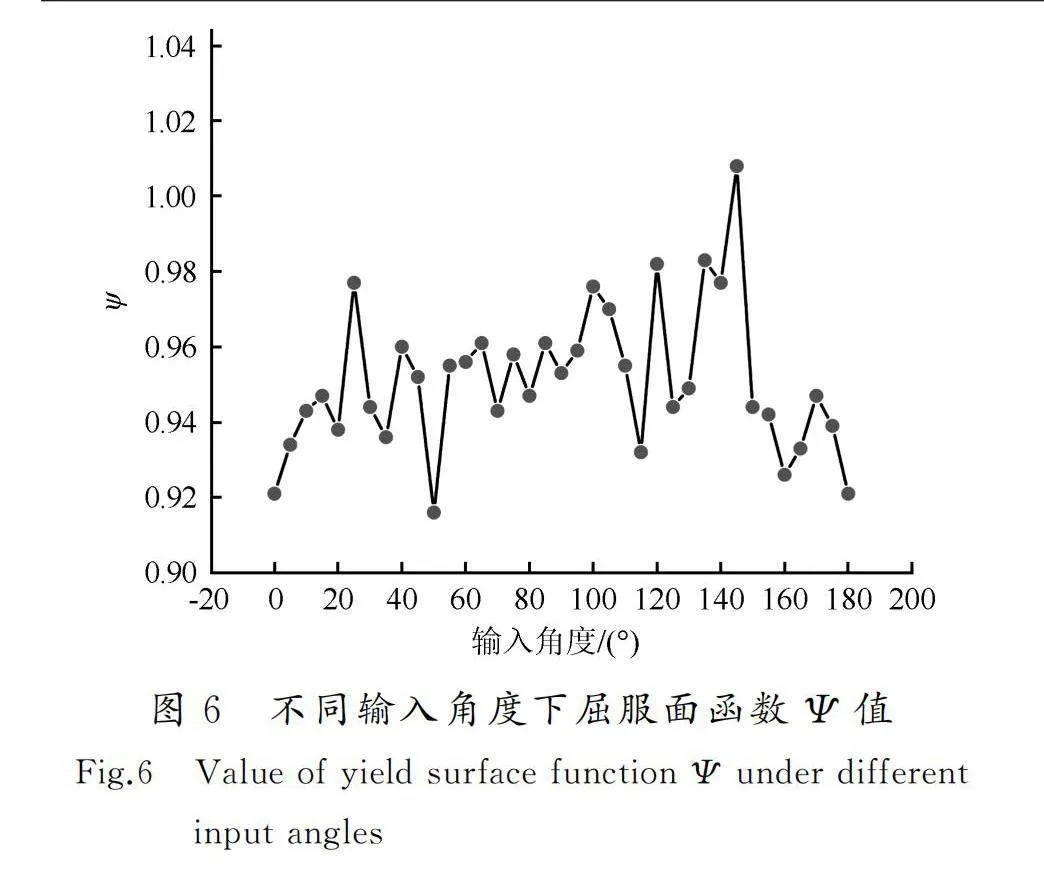
以22組近斷層地震動下橋墩所產生的地震反應平均值作為橋墩地震反應，采用恒載軸力與地震軸力最不利組合F_N，計算18號橋墩的墩底屈服彎矩M_y0及M_z0。沿0°方向輸入地震動時，順橋向為NS，橫橋向為EW，豎向為UP，22組地震波均為原始數據（未調幅）。地震動輸入角度θ為順橋向NS地震波與X軸方向、橫橋向EW地震波與Y軸方向的夾角。為尋找最不利輸入角度，保持輸入地震動三向正交不變，將地震動輸入方向沿0°方向順時針旋轉，每次增加5°。各個角度下的屈服面函數Ψ值列于表4（圖6）。

結合圖6、表4可以看出，屈服面函數Ψ在地震動145°輸入下最大，Ψ為1.008且大于1，這表明此時自復位橋墩達到屈服狀態。表4中屈服面函數值在除145°外的其他角度下均小于1，說明145°是三向地震動輸入時鐵路自復位橋墩的最不利輸入角度，且三向地震動輸入時墩底彎矩反應也大于順橋向或橫橋向單獨輸入。因此，自復位橋墩設計時若不考慮地震動最不利輸入方向，則偏于不安全。

4 結論

（1） 給出了能考慮多角度提離的鐵路自復位橋墩空間多彈簧模型建立方法，并與經過振動臺試驗驗證的兩彈簧模型結果進行比較，發現空間多彈簧模型可以較好地模擬自復位橋墩的地震反應。

（2） 提出了采用屈服面函數判別鐵路自復位橋墩地震動最不利輸入角度的方法。

（3） 鐵路自復位橋墩地震動最不利輸入方向不一定是順橋向或橫橋向。本研究中橋墩地震動最不利輸入角度為145°，在此方向下墩底彎矩反應大于順橋向和橫橋向輸入。自復位橋墩設計時若不考慮地震動最不利輸入方向，則偏于不安全。

參考文獻（References）

［1］中華人民共和國交通運輸部.公路橋梁抗震設計規范：JTG/T 2231-01—2020［S］.北京：人民交通出版社，2020.

Ministry of Transport of the People's Republic of China.Specifications for seismic design ofhighway bridges：JTG/T 2231-01—2020［S］.Beijing：China Communications Press，2020.

［2］TORBOL M，SHINOZUKA M.Effect of the angle of seismic incidence on the fragility curves of bridges［J］.Earthquake Engineering amp; Structural Dynamics，2012，41（14）：2111-2124.

［3］單德山，韓璐璐，瞿發憲，等.地震動入射角對空心薄壁高墩橋梁地震易損性的影響［J］.交通運輸工程學報，2020，20（6）：90-103.

SHAN Deshan，HAN Lulu，QU Faxian，et al.Impact of ground motion incident angles on seismic vulnerability for bridge with thin-walled hollow tall pier［J］.Journal of Traffic and Transportation Engineering，2020，20（6）：90-103.

［4］李小珍，洪沁燁，雷虎軍，等.地震動輸入方向對鐵路部分斜拉橋地震響應的影響［J］.橋梁建設，2015，45（1）：26-32.

LI Xiaozhen，HONG Qinye，LEI Hujun，et al.Effect of input directions of seismic ground motion on seismic responses of a railway extradosed bridge［J］.Bridge Construction，2015，45（1）：26-32.

［5］韓恩圳，何浩祥，呂永偉.三維地震動下結構最不利入射角度研究［J］.振動工程學報，2016，29（1）：132-139.

HAN Enzhen，HE Haoxiang，Lü Yongwei.Critical angle of structure subjected to three-dimensional ground motion［J］.Journal of Vibration Engineering，2016，29（1）：132-139.

［6］王滔，郭恩棟，張麗娜，等.大跨斜拉橋地震動最不利輸入方向分析［J］.世界地震工程，2007，23（4）：107-111.

WANG Tao，GUO Endong，ZHANG Li'na，et al.The critical direction of earthquake input for dynamic analysis of a long span cable-stayed bridge［J］.World Earthquake Engineering，2007，23（4）：107-111.

［7］LPEZ O A，TORRES R.The critical angle of seismic incidence and the maximum structural response［J］.Earthquake Engineering amp; Structural Dynamics，1997，26（9）：881-894.

［8］馮云田，李明瑞，林春哲.復雜結構的彈性地震反應分析［J］.地震工程與工程振動，1991，11（4）：77-86.

FENG Yuntian，LI Mingrui，LIN Chunzhe.Elastic earthquake response analysis for complex structures［J］.Earthquake Engineering and Engineering Vibration，1991，11（4）：77-86.

［9］范立礎，聶利英，李建中.復雜結構地震波輸入最不利方向標準問題［J］.同濟大學學報（自然科學版），2003，31（6）：631-636.

FAN Lichu，NIE Liying，LI Jianzhong.Discussion on standard of critical angle of seismic wave in seismic analysis of complicated structures［J］.Journal of Tongji University，2003，31（6）：631-636.

［10］HOUSNER G W.The behavior of inverted pendulum structures during earthquakes［J］.The Bulletin of the Seismological Society of America，1963，53（2）：403-417.

［11］司炳君，谷明洋，孫治國，等.近斷層地震動下搖擺-自復位橋墩地震反應分析［J］.工程力學，2017，34（10）：87-97.

SI Bingjun，GU Mingyang，SUN Zhiguo，et al.Seismic response analysis of the rocking self-centering bridge piers under the near-fault ground motions［J］.Engineering Mechanics，2017，34（10）：87-97.

［12］孫治國，趙泰儀，石巖，等.搖擺-自復位橋墩抗震性能數值建模方法研究［J］.應用基礎與工程科學學報，2019，27（6）：1357-1369.

SUN Zhiguo，ZHAO Taiyi，SHI Yan，et al.Research on numerical modeling method for rocking self-centering bridge piers［J］.Journal of Basic Science and Engineering，2019，27（6）：1357-1369.

［13］鐘正午，石巖，秦洪果，等.搖擺-自復位橋墩的多彈簧模型建模方法研究［J］.世界地震工程，2021，37（4）：197-205.

ZHONG Zhengwu，SHI Yan，QIN Hongguo，et al.Simulation method for multi-spring model of rocking self-centering pier［J］.World Earthquake Engineering，2021，37（4）：197-205.

［14］PALERMO A，PAMPANIN S，CALVI G M.Concept and development of hybrid solutions for seismic resistant bridge systems［J］.Journal of Earthquake Engineering，2005，9（6）：899-921.

［15］PALERMO A，PAMPANIN S，MARRIOTT D.Design，modeling，and experimental response of seismic resistant bridge piers with posttensioned dissipating connections［J］.Journal of Structural Engineering，2007，133（11）：1648-1661.

［16］PALERMO A，PAMPANIN S.Enhanced seismic performance of hybrid bridge systems：comparison with traditional monolithic solutions［J］.Journal of Earthquake Engineering，2008，12（8）：1267-1295.

［17］SOLBERG K，MASHIKO N，MANDER J B，et al.Performance of a damage-protected highway bridge pier subjected to bidirectional earthquake attack［J］.Journal of Structural Engineering，2009，135（5）：469-478.

［18］OU Y C，WANG P H，TSAI M S，et al.Large-scale experimental study of precast segmental unbonded posttensioned concrete bridge columns for seismic regions［J］.Journal of Structural Engineering，2010，136（3）：255-264.

［19］夏修身，陳興沖.鐵路高墩橋梁基底搖擺隔震與墩頂減震對比研究［J］.鐵道學報，2011，33（9）：102-107.

XIA Xiushen，CHEN Xingchong.Controlled rocking and pier top seismic isolation of railway bridge with tall piers［J］.Journal of the China Railway Society，2011，33（9）：102-107.

［20］XIA X S，ZHANG X Y，SHI J，et al.Seismic isolation of railway bridges using a self-centering pier［J］.Smart Structures and Systems，2021，27（3）：447-455.

［21］夏修身，陳興沖，李建中.高墩自復位隔震機理［J］.中南大學學報（自然科學版），2015，46（7）：2549-2557.

XIA Xiushen，CHEN Xingchong，LI Jianzhong.Isolation mechanism of self-centering tall pier［J］.Journal of Central South University （Science and Technology），2015，46（7）：2549-2557.

［22］夏修身，陳興沖.樁基礎高墩搖擺隔震分析模型研究［J］.鐵道學報，2013，35（11）：86-91.

XIA Xiushen，CHEN Xingchong.Study on analytical model for rocking isolation of tall piers with pile foundations［J］.Journal of the China Railway Society，2013，35（11）：86-91.

［23］夏修身，唐徑遙，韋性涵，等.自復位高墩振動臺模型試驗［J］.世界地震工程，2020，36（1）：109-117.

XIA Xiushen，TANG Jingyao，WEI Xinghan，et al.Shaking table test of self-centering model bridge pier［J］.World Earthquake Engineering，2020，36（1）：109-117.

［24］史軍，夏修身，唐徑遙.遠場長周期地震動對自復位高墩地震反應的影響［J］.地震工程與工程振動，2021，41（5）：249-255.

SHI Jun，XIA Xiushen，TANG Jingyao.Influence of far-field long-period ground motion on seismic response of self-centering high piers［J］.Earthquake Engineering and Engineering Dynamics，2021，41（5）：249-255.

［25］夏修身，李建中.近場地震動對樁基礎高墩搖擺反應的影響［J］.哈爾濱工業大學學報，2014，46（4）：82-86.

XIA Xiushen，LI Jianzhong.Effect of near-field ground motion on the rocking response of tall pier with pile foundations［J］.Journal of Harbin Institute of Technology，2014，46（4）：82-86.

［26］VAMVATSIKOS D，CORNELL C A.Incremental dynamic analysis［J］.Earthquake Engineering amp; Structural Dynamics，2002，31（3）：491-514.

［27］BRESLER B.Design criteria for reinforced columns under axial load and biaxial bending［J］.ACI Journal Journal，1960，57（11）：481-490.

［28］孟杰，劉釗.基于屈服面的曲線梁橋地震動最不利輸入方向［J］.振動與沖擊，2013，32（3）：115-118.

MENG Jie，LIU Zhao.Critical angle of seismic incidence for curved bridges based on a yield surface［J］.Journal of Vibration and Shock，2013，32（3）：115-118.

（本文編輯：趙乘程）