軸向拉壓式U型厚壁金屬波紋管阻尼器抗震性能研究

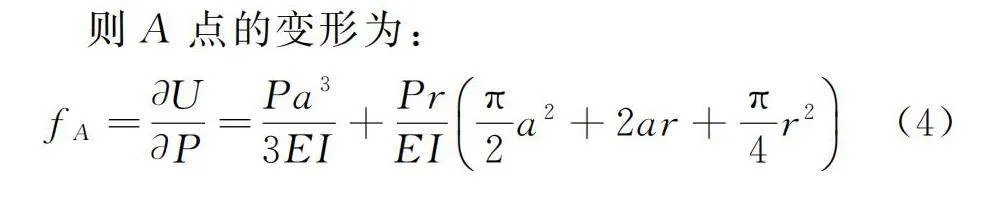
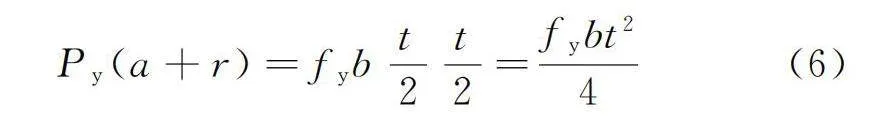
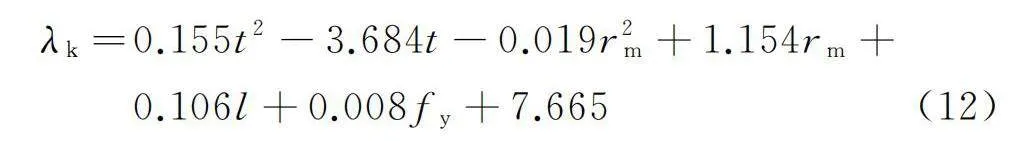
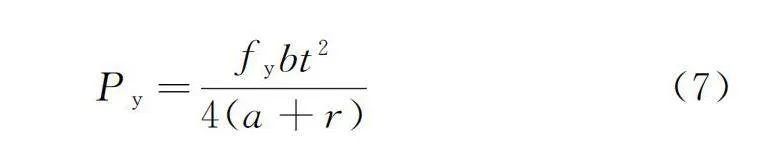
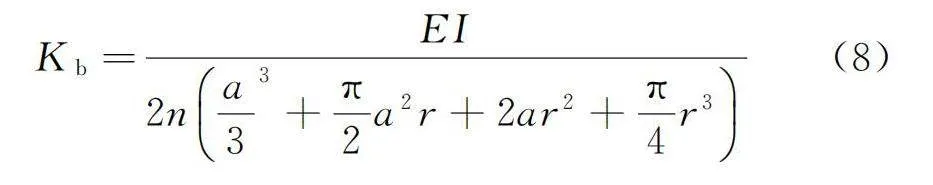
摘要： 針對傳統金屬阻尼器承載力不足、極限變形較小等問題，提出一種新型軸向拉壓式U型厚壁金屬波紋管阻尼器。通過改變波紋管的壁厚、內徑及波數等參數來調整阻尼器的承載力、初始剛度、極限變形及延性；采用有限元分析手段，對阻尼器的核心耗能元件進行單調及低周往復加載條件下的力學性能分析。研究核心耗能元件的內徑、壁厚、波紋平均半徑、U型波紋直邊長度、材料屈服強度及波數這6個獨立變量對其力學性能的影響關系，提出阻尼器極限位移的計算方法，給出阻尼器受拉屈服后剛度與屈服前剛度之比的擬合公式，揭示出新型阻尼器的受力機理，建立阻尼器的恢復力模型。同時，針對U型波紋管建立考慮邊波效應的修正簡化計算方法，并與規范法進行比較。研究結果表明：修正后的簡化分析方法與規范法相比具有更高的精度;阻尼器滯回曲線飽滿、耗能能力強、變形大、延性高;金屬波紋管的剛度、屈服荷載、屈服后剛度及極限荷載均隨壁厚的增加而顯著增大;隨著波數的增加，核心耗能元件的極限變形、延性及累積耗能顯著提高，但受拉屈服后剛度降低;建議阻尼器設計時波紋平均徑厚比不大于3.8，最大設計工作位移不大于極限位移的0.8倍。

關鍵詞： 厚壁金屬波紋管; 抗震性能; 金屬阻尼器; 有限元分析; ABAQUS

中圖分類號： TU352.1⁺1 文獻標志碼：A 文章編號： 1000-0844（2024）06-1318-13

DOI：10.20000/j.1000-0844.20230116003

Seismic performance of an axial compression-tension，

U-shaped， and thick-walled metal bellows damper

ZHENG Guozu^1，2， HAN Jianping^1，2

（1. School of Civil Engineering， Lanzhou University of Technology， Lanzhou 730050， Gansu， China;

2. Western Engineering Research Center of Disaster Mitigation in Civil Engineering

of Ministry of Education， Lanzhou 730050， Gansu， China）

Abstract： Traditional dampers often have low bearing capacity or poor deformation ability. To address these issues， this paper proposes a novel axial compression-tension， U-shaped， and thick-walled metal bellows damper. The performance of the damper can be changed by adjusting different parameters of the bellows. For example， increasing the wall thickness and inner diameter of the bellows can improve the bearing capacity and initial stiffness of the damper， and increasing the number of convolutions of the bellows can increase its ultimate deformation and ductility. The mechanical characteristics of energy-dissipation elements of the damper were analyzed under monotonic and cyclic loads using the finite element method. The influence of six independent variables on the mechanical properties of energy-dissipation elements was studied， including inner diameter， wall thickness， average convolution radius， straight edge length of U-shaped convolution， material yield strength， and convolution number. A method for calculating the ultimate displacement of the damper was developed， and a fitting formula for the ratio of post-yield stiffness to pre-yield stiffness was put forward. In addition， the stress mechanism of the novel damper was revealed， and the restoring force model of the damper was established. A simplified calculation method was developed for U-shaped bellows. The method was later corrected to consider the end convolution effect and then compared to the standard method. The results show that the correction method has higher accuracy than the standard method. The novel damper has a large deformation capacity， excellent ductility， and a full hysteresis loop， clearly showing its outstanding energy-dissipation capability. As the wall thickness increases， the stiffness， yield load， post-yield stiffness， and ultimate load of metal bellows increase significantly. As the number of convolutions increases， the ultimate deformation， ductility， and accumulated energy dissipation of metal bellows increase significantly， while its post-yield stiffness under tension decreases. It is suggested that the average aspect ratio of convolution should not exceed 3.8， and the maximum design displacement should be less than 0.8 times of ultimate displacement when designing the damper.

Keywords： thick-walled metal bellows; seismic performance; metal damper; finite element analysis; ABAQUS

0 引言

金屬阻尼器是一種耗能機理明確、制作簡單、成本低廉、易于更換和性能穩定的減震耗能裝置。它既可以當作耗能元件配合隔震支座或耗能支撐使用，又可以單獨安裝于結構中，為其提供附加阻尼和剛度，因此具有廣泛的應用前景^［1-3］。目前，國內外學者針對金屬阻尼器提出了許多不同的構造形式并進行了相關研究。文獻［4-7］以U型鋼板剪切變形耗能為基礎，構造了圓環型阻尼器、并聯圓環型阻尼器及帶有U型鋼帶的金屬阻尼器，并通過試驗研究發現，這類阻尼器通常具有較大的極限變形，但承載力普遍偏低。Demir等^［8］提出了一種鋸齒形金屬阻尼器；其利用金屬的彎曲變形進行耗能，滯回性能穩定，拉壓強度幾乎完全相等，且變形能力強，但缺點仍然是承載力不高。Lotfi Mahyari等^［9］提出了一種純扭轉屈曲型金屬阻尼器，并通過理論推導和試驗研究發現，該阻尼器變形能力極強，滯回性能穩定，但其初始剛度及極限承載力均很低。鄧開來等^［10］對5個形狀優化的變截面軟鋼剪切阻尼器進行了擬靜力試驗研究，發現該阻尼器屈服位移較小，承載能力較強，但極限變形能力有限。吳山等^［11］提出了一種多階段屈服及失效型金屬套管阻尼器，發現其具有較低的屈服位移，能夠很快屈服耗能，但最大破壞位移相對較小。胡大柱等^［12］提出了一種軸向布置的金屬阻尼器，以解決某些金屬阻尼器需要斜撐對稱布置的技術問題，通過擬靜力試驗發現：該阻尼器具有較高的承載力，但其極限變形較低且滯回曲線存在捏攏效應。 文獻［13-16］中提出在鋼管中灌入金屬鉛，研發了一種鋼管鉛阻尼器，利用其剪切變形進行耗能；這種阻尼器的特點是初始剛度大、屈服位移小（1 mm即可進入耗能狀態）、承載力較高、延性系數大，但其極限變形能力不高。

金屬波紋管是一種子午線呈波紋狀的旋轉殼，按波形可分為“U型”“Ω型”“S型”等多種類型，廣泛用于儀器儀表、航空航天及石油化工等行業。金屬波紋管的主要作用是補償管線或容器由于熱脹冷縮等原因產生的位移，同時也具有減振降噪等功能以及很強的軸向變形能力。土木工程行業中對其研究相對較少。Xiang等^［17］針對地下管道系統中波紋管接頭容易在較強地震作用下產生斷裂、壓碎及彎曲等破壞問題，開展了金屬波紋管的低周往復試驗及有限元分析，研究發現多波波紋管與單波波紋管接頭的承載力幾乎相同，但能量吸收隨波數的增加呈線性增加。Motamedi等^［18］對4組不銹鋼材料制作的金屬波紋管進行了軸向低周往復試驗，同時利用數值模擬手段探索了波紋管的形狀、厚度、直徑和長度等參數對其力學性能的影響，研究表明：不銹鋼波紋管具有較強的變形能力和耗能能力，但由于所選試件壁厚較小，屬于薄壁波紋管，以至于其承載力不高。文獻［19-20］對波紋鋼管鉛阻尼器進行了數值分析與試驗研究，認為其初始剛度大、屈服位移小、滯回曲線飽滿、承載力較高，但由于該阻尼器是利用剪切變形進行耗能，導致其變形能力有限。

綜上所述，目前常見的金屬阻尼器雖然種類眾多，但大多數都很難同時實現高承載力與大變形的統一，部分阻尼器還存在初始剛度低等問題。在實際工程應用中對阻尼器的性能提出了更高要求，性能優越的金屬阻尼器應該具有較大的初始剛度、較強的變形能力和較高的承載能力：大的初始剛度能使其在荷載作用下很快屈服耗能，較高的變形能力應保證阻尼器的極限位移大于建筑結構變形達到塑性層間位移角時對其位移的需求。例如，按3 m層高考慮的鋼結構，其塑性層間位移角為1/50，當阻尼器的變形與層間位移為1∶1時，其需求位移為60 mm。對于層高更高或選用具有位移放大功能安裝方式的阻尼器來說，其需求位移將更大。另外，土木工程結構對于阻尼器的承載力需求從數噸到數百噸不等，性能優越的金屬阻尼器的承載力應能涵蓋絕大多數的結構需求。因此，亟需一種初始剛度高、變形能力強、承載力在較大范圍內可調的金屬阻尼器。

鑒于此，本文提出一種軸向拉壓式U型厚壁金屬波紋管阻尼器（Axial compression-tension，U-shaped and Thick-walled Metal Bellows Damper，AUTMBD）。該阻尼器采用厚壁金屬波紋管（壁厚大于3 mm）制作，可通過增大波紋管壁厚和內徑來顯著提高承載能力和初始剛度，通過改變波數來調節變形能力及延性，通過并聯布置來使阻尼器實現拉壓等強。本文首先提出了AUTMBD的構造和安裝方式，建立了考慮邊波效應的修正簡化分析方法;其次，利用有限元軟件ABAQUS對19個單一U型厚壁金屬波紋管進行了參數分析，研究單調加載及低周往復加載下AUTMBD的力學性能，分析其內徑、壁厚、波紋平均半徑、U型波紋直邊長度、材料屈服強度及波數等參數對其力學性能的影響;最后，建立了金屬波紋管的恢復力模型。

1 AUTMBD的構造與工作原理

1.1 基本構造

AUTMBD的基本構造如圖1所示，主要由厚壁金屬波紋管、端板和連接接頭3部分組成。厚壁金屬波紋管兩端為平直段，中間為正反相連的U型波紋段，端板與金屬波紋管的平直段通過焊接方式連接，接頭采用銷軸連接方式，確保金屬波紋管只在軸力作用下發生變形。

1.2 核心耗能元件基本尺寸

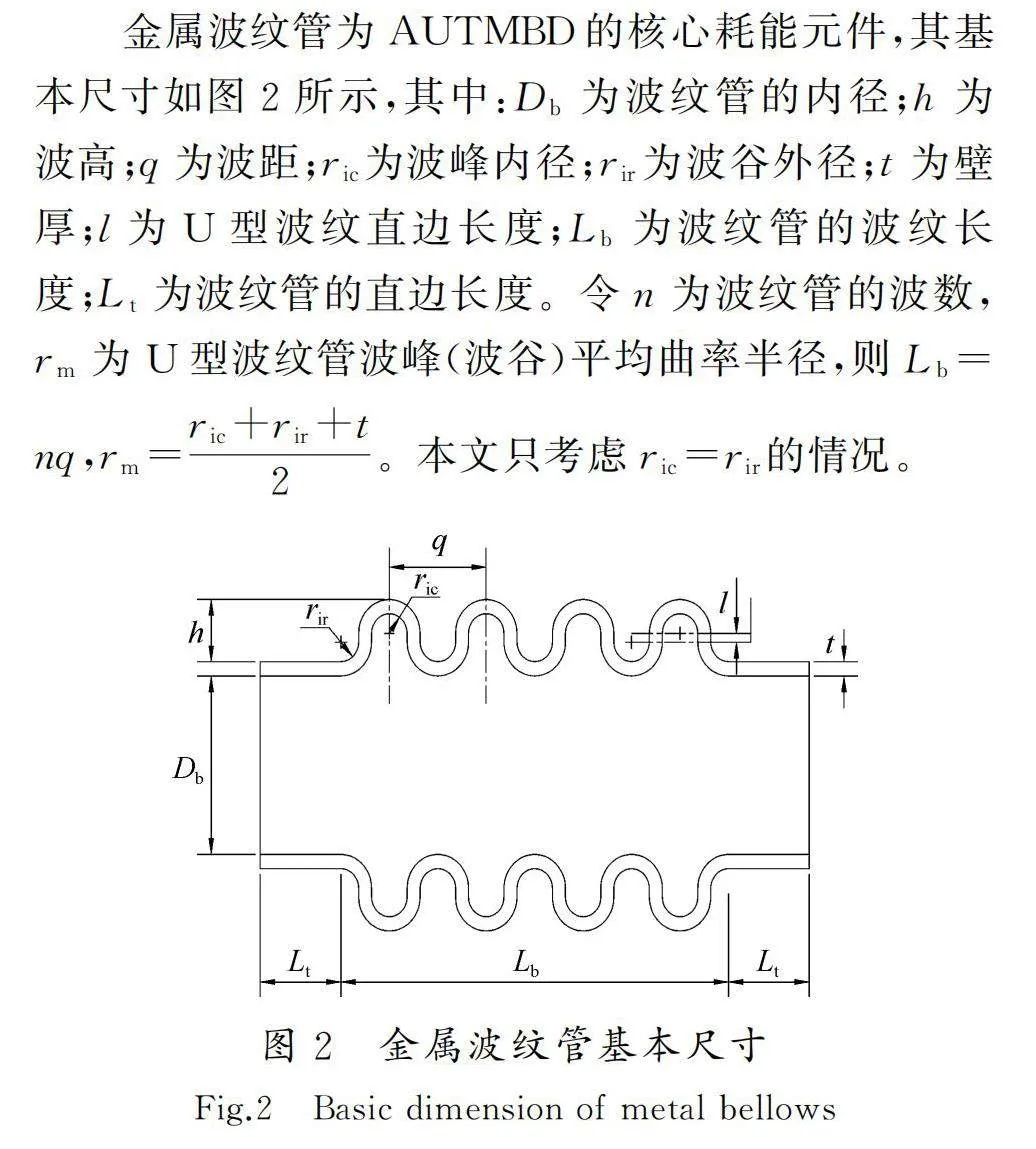
金屬波紋管為AUTMBD的核心耗能元件，其基本尺寸如圖2所示，其中：D_b為波紋管的內徑;h為波高;q為波距;r_ic為波峰內徑;r_ir為波谷外徑;t為壁厚;l為U型波紋直邊長度;L_b為波紋管的波紋長度;L_t為波紋管的直邊長度。令n為波紋管的波數，r_m為U型波紋管波峰（波谷）平均曲率半徑，則L_b=nq，r_m=r_ic+r_ir+t/2。本文只考慮r_ic=r_ir的情況。

1.3 工作原理

AUTMBD主要依靠金屬塑性變形進行耗能，屬于位移相關型阻尼器。在軸向荷載作用下，它能將塑性變形集中于波紋段，所有波峰、波谷均可全截面屈服耗能，耗能效率高。AUTMBD的變形能力與波數成正比，理論上其極限變形可通過增加波數來無限增大，因此，它能夠滿足結構對阻尼器大變形的需求。此外，AUTMBD的剛度、屈服荷載和極限承載力均可通過加大波紋管的壁厚和內徑來顯著提高。文獻［17］指出，波紋管的屈服承載力與壁厚的1.5次方成正比。因此，通過改變波紋管的壁厚和內徑可以滿足結構對阻尼器不同承載力的需求。

AUTMBD工作時，主要利用金屬波紋管軸向變形進行耗能，由于其自身可以發生多波屈曲，相比屈曲約束支撐而言，無需附加約束裝置，損傷部位無遮擋，因而具有材料用量少及損傷情況易于觀察的優點。

1.4 結構中的布置形式

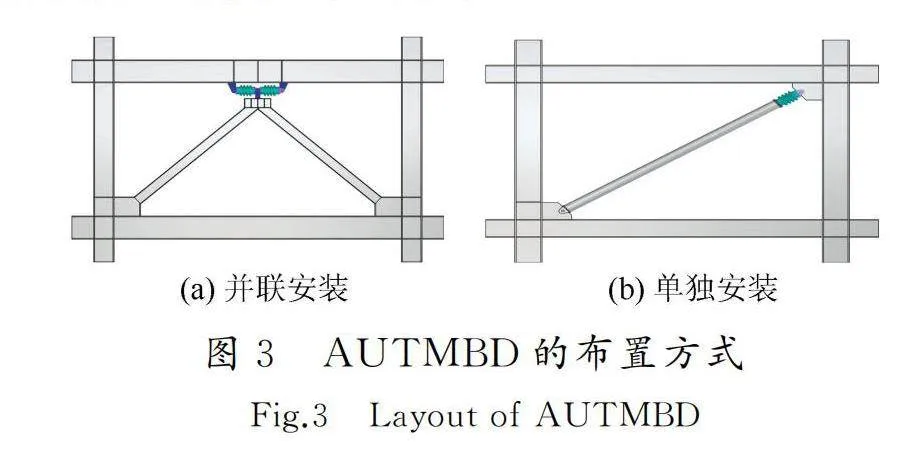
AUTMBD結合結構中的支撐使用最為方便，圖3為AUTMBD的安裝示意圖，分別為并聯安裝方式和單獨安裝方式。并聯安裝時，阻尼器整體承載力將會顯著提高。同時，由于工作時AUTMBD總是一個受壓另一個受拉，因此，無論結構層間位移是正還是負，AUTMBD的承載力之和總是相等，對于結構來說，這種安裝方式實現了拉壓等強。AUTMBD的受力特點之一是其受拉承載力大于受壓承載力，因此，在單獨安裝方式中會存在拉壓不等強的問題，在工程應用時應注意限制其拉壓不等強系數。AUTMBD的拉壓不等強系數隨工作位移增大而增大，隨波紋管壁厚的增加而顯著降低，在對AUTMBD進行設計時，可以通過降低最大工作位移與極限位移的比值以及增大壁厚來降低拉壓不等強系數，以滿足工程需求。

2 AUTMBD的簡化力學分析方法

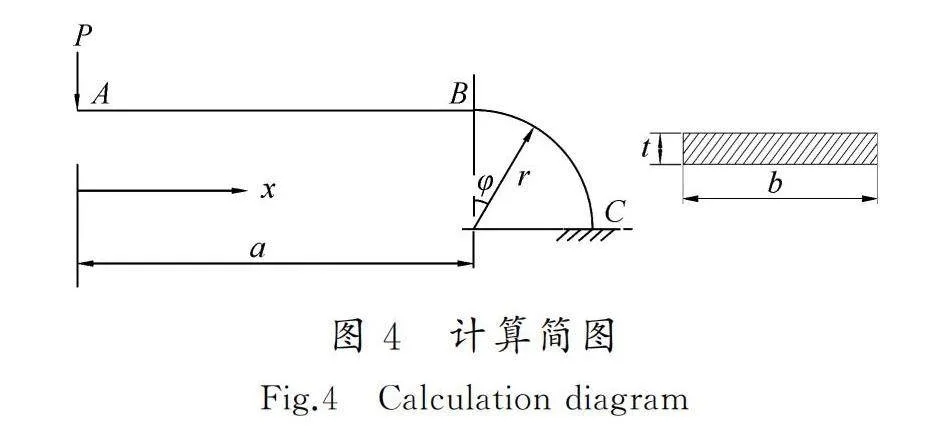
AUTMBD由于具有對稱性，可以采用四分之一波進行分析。簡化分析方法將波紋管波峰和波谷的圓環板及圓環殼分別等效為平板和柱殼，其截面寬度分別取圓環板與圓環殼的平均周長，高度為波紋管的壁厚，波谷與波峰在環板處串聯。圖4為四分之一波簡化計算簡圖。波紋管剛度計算時，先分別計算單個波峰和波谷的剛度，即計算圖4中模型剛度的一半，再計算單個波峰與波谷串聯后的剛度，最后除以波數n，即為波紋管的剛度。該簡化方法計算所得剛度偏低，原因在于未考慮邊波效應的影響。文獻［21］通過試驗發現，1號試件全部9個波的位移量平均為中間8個波位移量的1.065倍，邊波的剛度明顯大于中間波，即存在邊波效應。據此，對簡化計算方法進行修正，修正方法為對邊波乘以按文獻［21］計算所得的邊波效應系數1.923，然后與中間波剛度串聯。對于屈服荷載則乘以屈服荷載修正系數λ_p進行修正。λ_p數值上等于按邊波效應修正后的剛度與未修正剛度的比值。

金屬波紋管的簡化分析方法推導過程如下：

如圖4所示，當A端作用荷載P時，直線段AB任意截面所受彎矩為：

M₁=Px， 0≤x≤a （1）

式中：x為任意截面到荷載作用點A的水平距離;a為荷載作用點A到圓弧起點B的水平距離，在數值上a=l/2，l為U型波紋直邊長度。

圓弧段BC所受彎矩為：

M₂=P（a+rsinφ）， 0≤φ≤π/2 （2）

式中：r為U型波紋管波峰（波谷）平均曲率半徑，即r=r_m=r_ic+r_ir+t/2;φ為圓弧段任意截面從B點開始轉過的角度。

ABC段的彎曲變形能為：

U=1/2EI∫^a₀P²x²dx+1/2EI∫^π/2₀P²（a+rsinφ）²rdφ=

P²a³/6EI+P²r/2EIπ/2a²+2ar+π/4r²（3）

式中：E為材料的彈性模量;I為截面慣性矩，對于圖中矩形截面，I=bt³/12，t為波紋管壁厚，b為等效截面寬度，數值上等于波峰或波谷的平均周長。

則A點的變形為：

f_A=?U/?P=Pa³/3EI+Pr/EIπ/2a²+2ar+π/4r²（4）

剛度為：

K=P/f_A=EI/a/3³+π/2a²r+2ar²+π/4r³ （5）

令材料屈服強度為f_y，波紋管屈服荷載為P_y，對應于C點全截面屈服時的荷載，則由C點截面彎矩平衡得：

P_y（a+r）=f_ybt/2t/2=f_ybt²/4 （6）

則：

P_y=f_ybt²/4（a+r） （7）

對于n波金屬波紋管，其剛度為：

K_b=EI/2na/3³+π/2a²r+2ar²+π/4r³ （8）

3 核心耗能元件有限元參數化分析

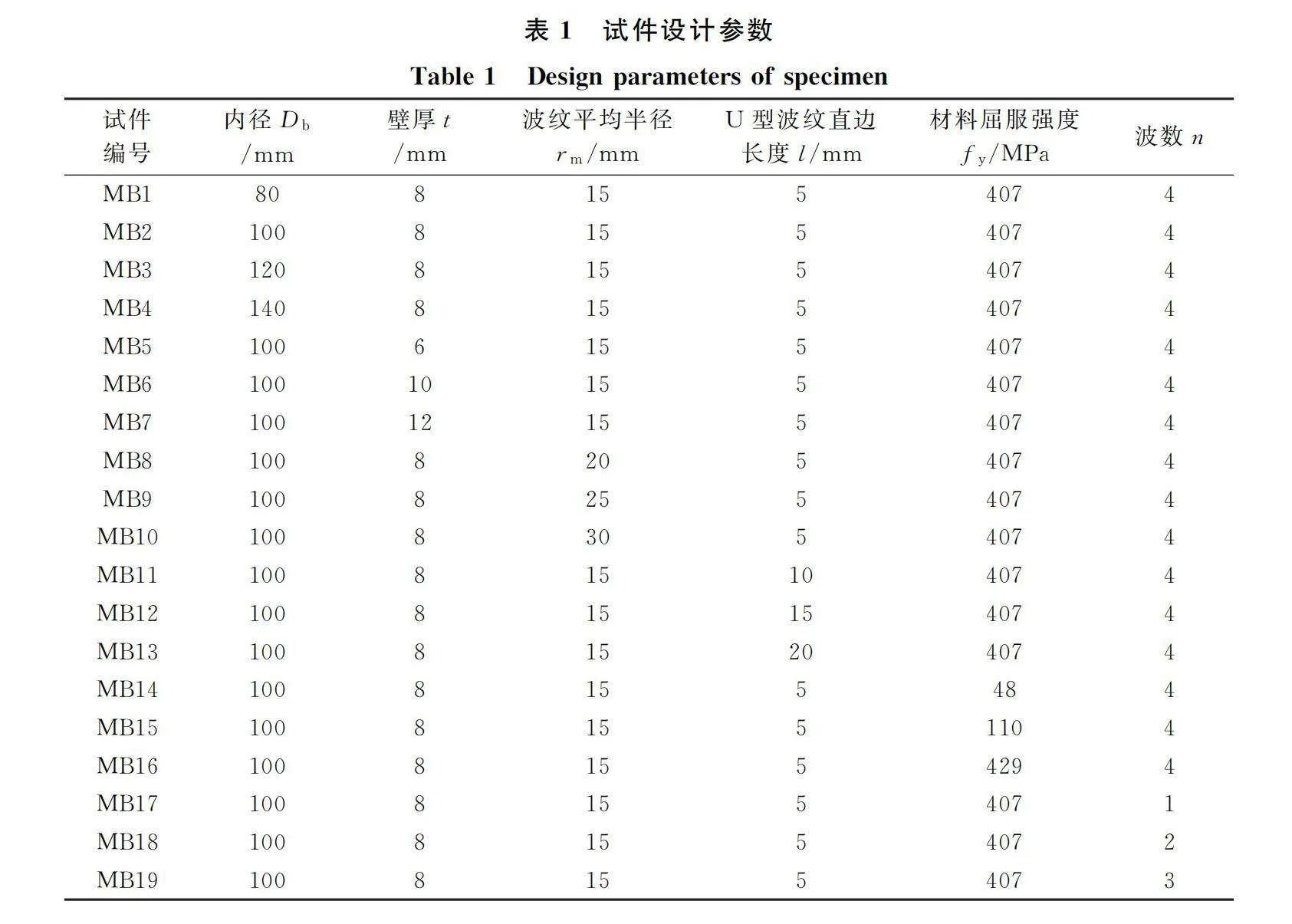
金屬波紋管作為AUTMBD的核心耗能元件，其形狀對AUTMBD力學性能影響很大，因此，有必要對其進行參數化分析，以明確各個參數對其力學性能的影響關系。影響波紋管力學性能的參數主要有內徑、外徑、波高、波距、波數、波峰內徑、波谷外徑、壁厚、材料強度等級、厚徑比和波深系數等。但這些參數并不獨立，如波高和波距與波峰內徑及波谷外徑直接相關，外徑與波紋管壁厚及波峰內徑和波谷外徑相關，因此，這里只考察內徑D_b、壁厚t、波紋平均半徑r_m、U型波紋直邊長度l、材料屈服強度f_y和波數n這6個獨立變量對波紋管力學性能的影響。每個變量考慮4種水平，均勻構造19個試件進行有限元分析。試件的設計參數如表1所列。

數值模擬時，材料屈服強度考慮了LYP100、LYP160、Q235及Q345四種等級。為了使有限元模擬更加準確，四種鋼材的材料性能參數分別采用文獻［22-24］中經過試驗數據標定后的數值。強化準則采用Von Mises流動法則，同時考慮各向同性強化和隨動強化特征。利用ABAQUS中的Combined 模塊和Cycle hardening材料屬性對19個試件進行模擬，所采用的材料參數如表2所列。表中：σ|₀為等效塑性應變為0時的應力;Q_∞為屈服面最大變化值;w為屈服面隨著塑性應變的增加而變化的比率;C_k和γ_k分別為隨著塑性應變的增加而變化的背應力變化系數和變化率，根據試驗數據進行校對；k為背應力個數；C_k/γ_k是背應力的最大變化值。

有限元分析主要考察上述6個獨立變量對金屬波紋管的極限位移、剛度、屈服荷載、屈服位移、拉壓不等強系數、能量耗散系數、黏滯阻尼系數等性能的影響。荷載施加考慮單調壓縮、單調拉伸及低周往復3種情況。低周往復加載制度根據ATC-24^［25］建議，在波紋管屈服前分別按照0.25倍、0.5倍、0.7倍的屈服位移加載;當加載至1.0倍的屈服位移后，采用1.0倍、1.5倍、2.0倍、3.0倍、5.0倍、7.0倍、8.0倍屈服位移以及波紋管受壓極限位移進行加載。每級循環圈數對于1.0倍屈服位移前，循環2圈；對于1.0倍屈服位移及以后各級，前3級循環3圈，其余循環2圈。

3.1 單調加載

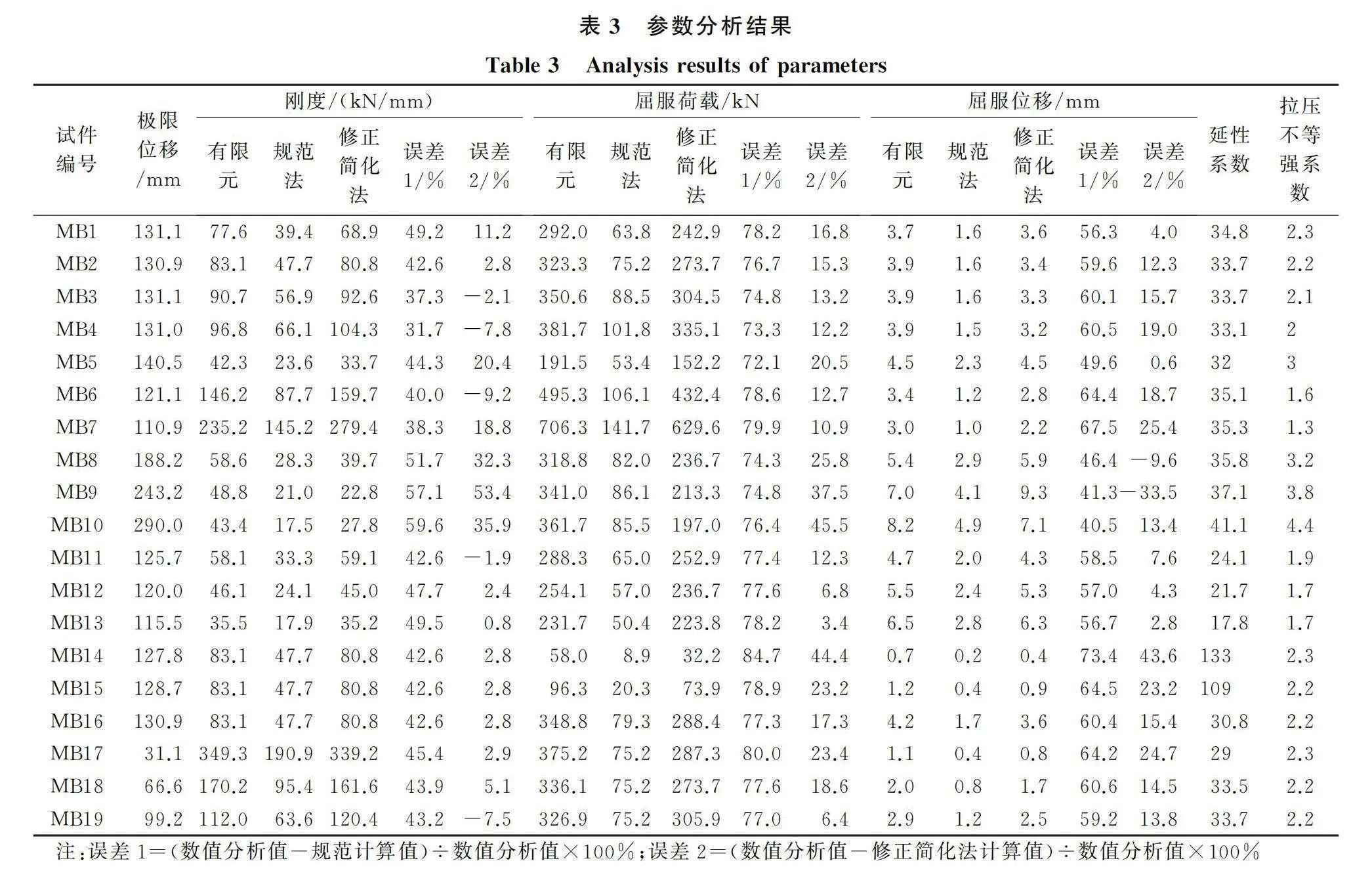
單調加載分為單調壓縮與單調拉伸兩種情況，分析結果如表3所列。表中剛度為金屬波紋管屈服前受壓與受拉剛度的平均值，屈服荷載與屈服位移均為受拉情況下的數值（受壓狀態下部分試件由于局部畸變屈曲嚴重，屈服荷載與屈服位移可靠性不高，不予采用）。金屬波紋管受拉極限位移遠大于受壓極限位移，因此，表中的極限位移均為受壓時的數值。金屬波紋管的剛度、屈服荷載和屈服位移分別采用本文簡化分析方法和壓力容器波形膨脹節^［26］中的方法（簡稱規范法）進行分析與對比。從表3可以看出，總體上，試件的延性系數均很高，且多波波紋管都具有很強的變形能力，遠大于一般建筑的需求。同時，其屈服荷載也很高，拉壓不等強系數隨著壁厚的增加而急劇減小，因此是一種非常理想的耗能元件。

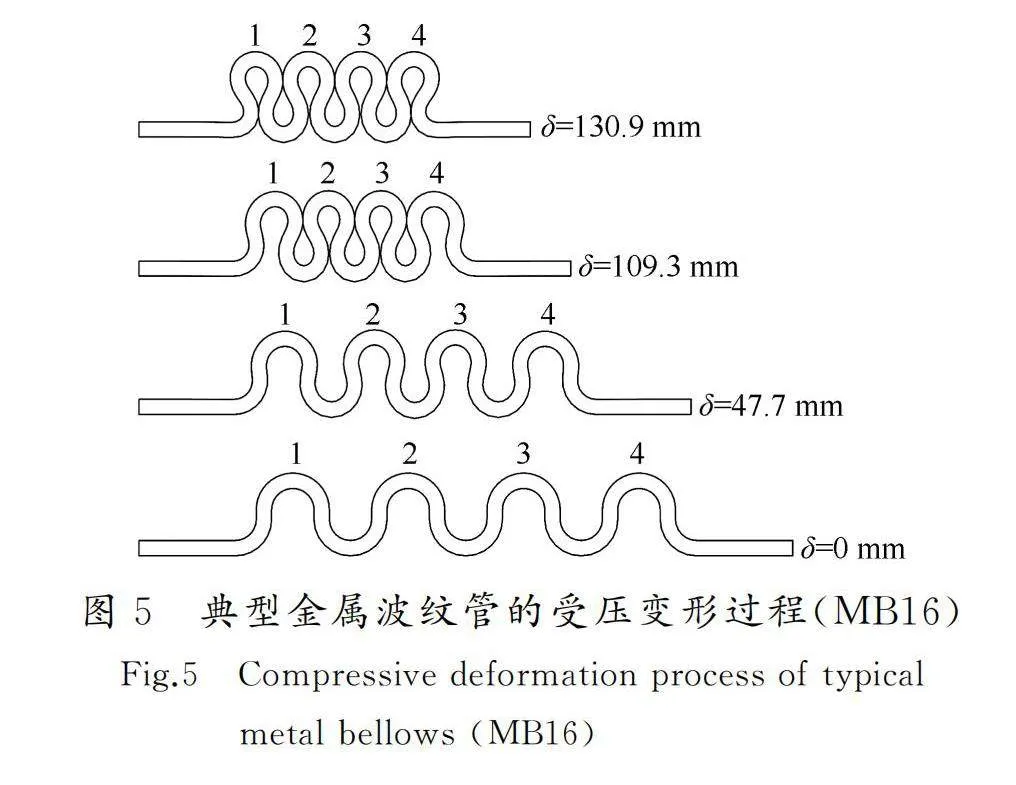
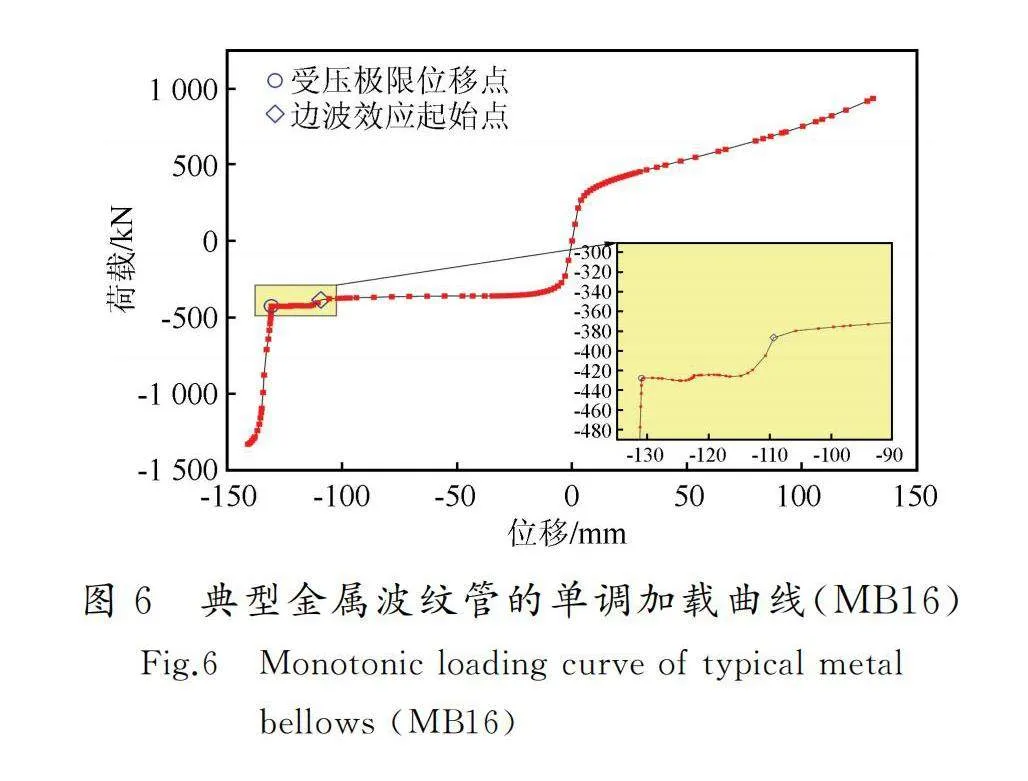
典型單個金屬波紋管受壓時的變形過程如圖5所示，單調加載曲線如圖6所示。圖5顯示了試件MB16在受壓位移（δ）分別為0.0、47.7、109.3及130.9 mm時的變形圖。由圖5可以看出，金屬波紋管受壓時的變形并不是均勻分布的。當δ=47.7 mm時，中間波2和3的變形相當，邊波1和4的變形相當，且邊波的變形小于中間波，這就是金屬波紋管的邊波效應，即由于波紋管直邊段（圖2中的L_t部分）約束剛度較大，出現其邊波剛度大于中間波的現象;當δ=109.3 mm時，可以更明顯地觀察到邊波效應，即中間波2和3的波壁均已相互接觸，無法繼續變形，但邊波1和4還可以承受一定變形，荷載-位移曲線中會表現出剛度的第一次突變，對應于圖6中的邊波效應起始點;當δ=130.9 mm時，對應于試件MB16的極限受壓狀態，即繼中間波之后，邊波的波壁剛好接觸，如果此時繼續增加位移，將會進一步擠壓波紋管的直邊段，直至波紋管壓屈，荷載-位移曲線中將會出現剛度的再一次突變，該狀態對應于圖6中的受壓極限位移點。由于金屬波紋管受拉時的極限變形遠大于其受壓值，因此，應將受壓時的極限位移作為波紋管的極限位移，該位移也是AUTMBD的極限位移。

由圖6可知，金屬波紋管受壓屈曲后荷載-位移曲線較為平緩，在達到極限位移之前會經歷一次剛度突變，對應于圖中的邊波效應起始點。同時，其受拉屈服后剛度明顯大于受壓屈服后剛度。受拉時，荷載-位移曲線先呈線性增加，在金屬波紋管屈服后，當位移約為屈服點至極限位移的一半時，荷載-位移曲線呈遞增趨勢。經擬合分析，該曲線符合一元二次方程，但曲線變化較為平緩，受拉屈服后，若按直線擬合，仍具有較高精度，可滿足工程需求。

（1） 不同參數對金屬波紋管性能的影響

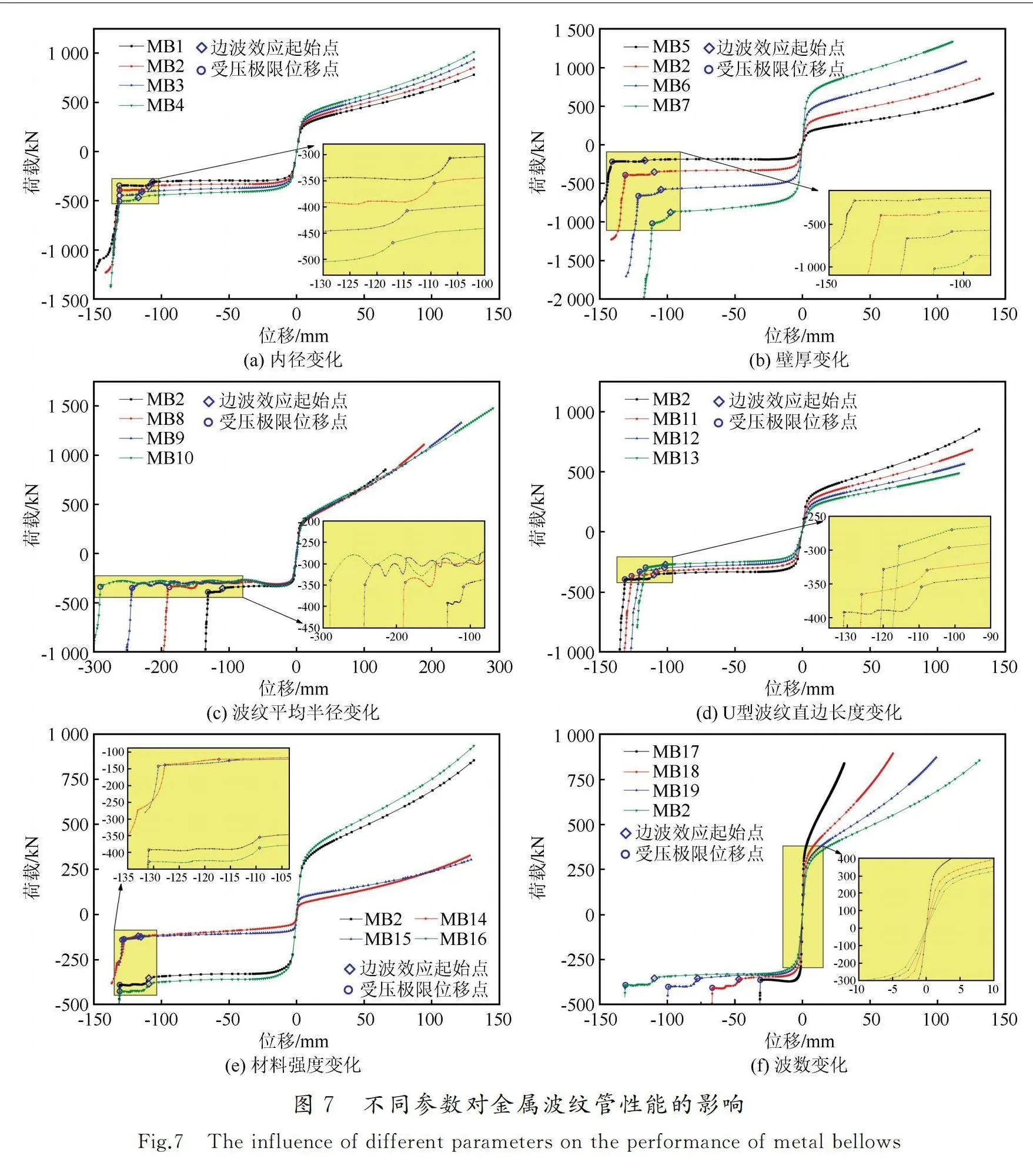
金屬波紋管的內徑D_b、壁厚t、波紋平均半徑r_m、U型波紋直邊長度l、材料屈服強度f_y和波數n這6個獨立變量單獨變化時對其性能的影響如圖7所示。

由圖7（a）可知，金屬波紋管內徑的變化對其極限位移沒有影響，金屬波紋管的剛度（以下均指屈服前剛度）、屈服荷載、受壓屈服后剛度、受拉屈服后剛度、受壓極限荷載及受拉極限荷載均隨著內徑的增大而增大，邊波效應起始點至受壓極限位移點的距離隨著內徑的增大而減小。

圖7（b）顯示了壁厚變化對金屬波紋管性能的影響。隨著壁厚的增加，金屬波紋管的剛度、屈服荷載、受壓屈服后剛度、受拉屈服后剛度、受壓極限荷載及受拉極限荷載顯著增加，且受壓極限荷載越來越接近受拉極限荷載，即拉壓不等強系數呈減小趨勢;波紋管的極限位移隨壁厚的增加而減小;邊波效應的剛度突變隨著壁厚的增加更加明顯。

圖7（c）展示了波紋平均半徑變化對金屬波紋管性能的影響。結合表3可知：金屬波紋管平均半徑越大，其極限位移及拉壓不等強系數越大;受壓屈服后，剛度越小，荷載-位移曲線“波動”越大。這是因為金屬波紋管的厚徑比越來越小，局部變形更加明顯，應力重分布現象也愈加顯著。

圖7（d）顯示了波紋管U型波紋直邊長度變化對其性能的影響。結合表3可知，金屬波紋管的剛度、屈服荷載、受壓屈服后剛度、受拉屈服后剛度、極限位移、拉壓不等強系數、受壓極限荷載及受拉極限荷載均隨著U型波紋直邊長度的增加而降低。

圖7（e）展示了材料屈服強度對金屬波紋管性能的影響。材料屈服強度越高，金屬波紋管的屈服荷載也相應越高，極限位移略有降低，但剛度幾乎不變;金屬波紋管的受壓屈服后剛度與材料屈服強度關系不大，受拉屈服后剛度與材料的屈服強度及硬化參數有關;通過MB14和MB15的對比分析可知，材料屈服強度接近時，硬化參數將對受拉屈服后剛度產生較大影響。

圖7（f）為波數變化對波紋管性能的影響關系。經對比分析可知，波數變化對金屬波紋管的極限位移及受拉屈服后剛度有顯著影響，隨著波數的增加，極限位移成倍增加;屈服荷載、極限荷載（包括受拉和受壓）及受壓屈服后剛度變化不大;受拉屈服后剛度隨波數的增加急劇減小，金屬波紋管的屈服前剛度也隨波數的增加而減小，與波數呈反比。

（2） 極限位移

AUTMBD的極限位移是其重要設計參數之一，與金屬波紋管的幾何參數密切相關。理論上波峰與波谷的凈距之和為其極限位移的上限，記為δ_th，則

δ_th=2n（2r_m-t） （9）

實際上，波峰與波谷的凈距不可能完全被擠壓消除。AUTMBD的實際極限位移記為δ_re，則δ_re必定小于δ_th。定義極限位移系數λ，使

δ_re=λδ_th （10）

由表3可知，影響極限位移系數λ的因素主要有波紋平均半徑r_m、U型波紋直邊長度l、波紋管厚度t、材料屈服強度f_y和波數n。通過對有限元數據的擬合可得：

λ=0.006t-0.007l-0.021 4r_m+0.001 03r²_m-0.000 017 8r³_m+0.000 072f_y+0.231n-0.081 3n²+0.008 9n³+0.658（11）

極限位移系數擬合值與有限元模擬結果的對比如圖8所示。可以看出考慮多因素影響的極限位移系數擬合值精度較高（R²=0.986），能夠滿足工程需求。此外，極限位移系數總體上在0.6～0.8之間變化，保守設計時可直接按0.6進行計算。

（3） 屈服后剛度

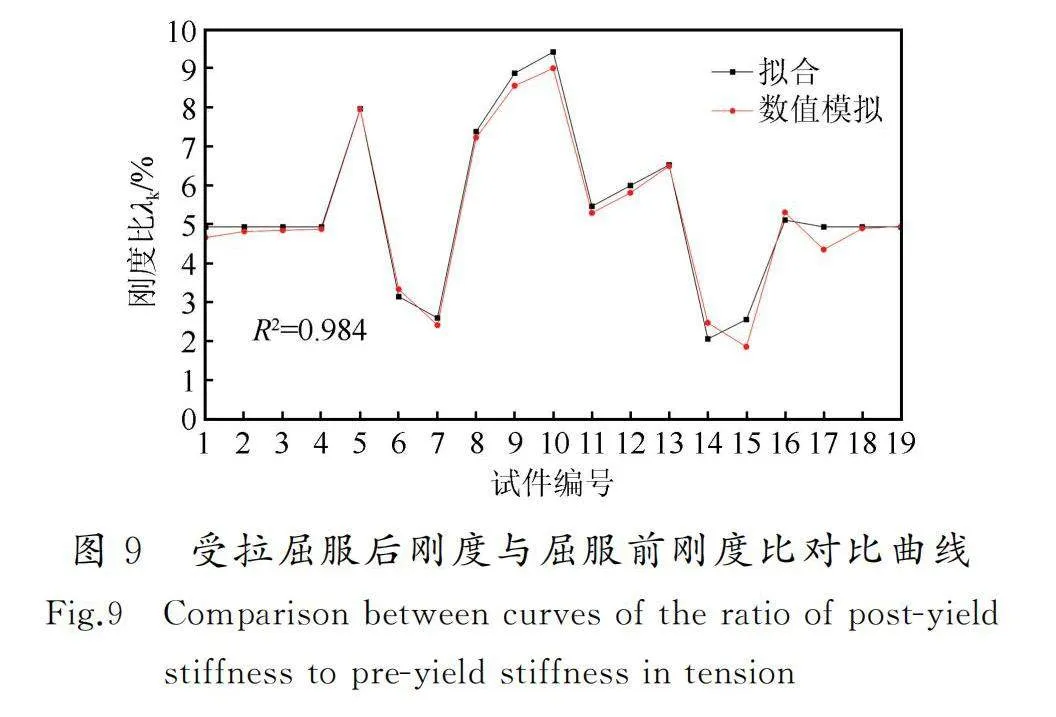
金屬波紋管的屈服后剛度包括受壓屈服后剛度和受拉屈服后剛度，前者通常較低。通過對19個試件的有限元結果進行分析可知：試件的受壓屈服后剛度平均值為0.39 kN/mm，受壓屈服后剛度與屈服前剛度的比值平均為0.42%，因此，可近似將受壓屈服后剛度取為0。受拉屈服后剛度主要與波紋管壁厚、波紋平均半徑、U型波紋直邊長度及材料屈服強度和硬化參數等密切相關。波紋管壁厚越大，受拉屈服后剛度與屈服前剛度的比值（記為λ_k）越小;波紋平均半徑越大λ_k越大，U型波紋直邊長度越長，λ_k越大;材料屈服強度和硬化參數越高λ_k越大。根據上述結論，對19個試件的受拉屈服后剛度進行擬合，得到受拉屈服后剛度與屈服前剛度的比值為：

λ_k=0.155t²-3.684t-0.019r²_m+1.154r_m+0.106l+0.008f_y+7.665（12）

金屬波紋管受拉屈服后剛度與屈服前剛度比值（%）的擬合值與有限元結果的對比如圖9所示。可以看出擬合精度較高（R²=0.984），滿足工程需求。

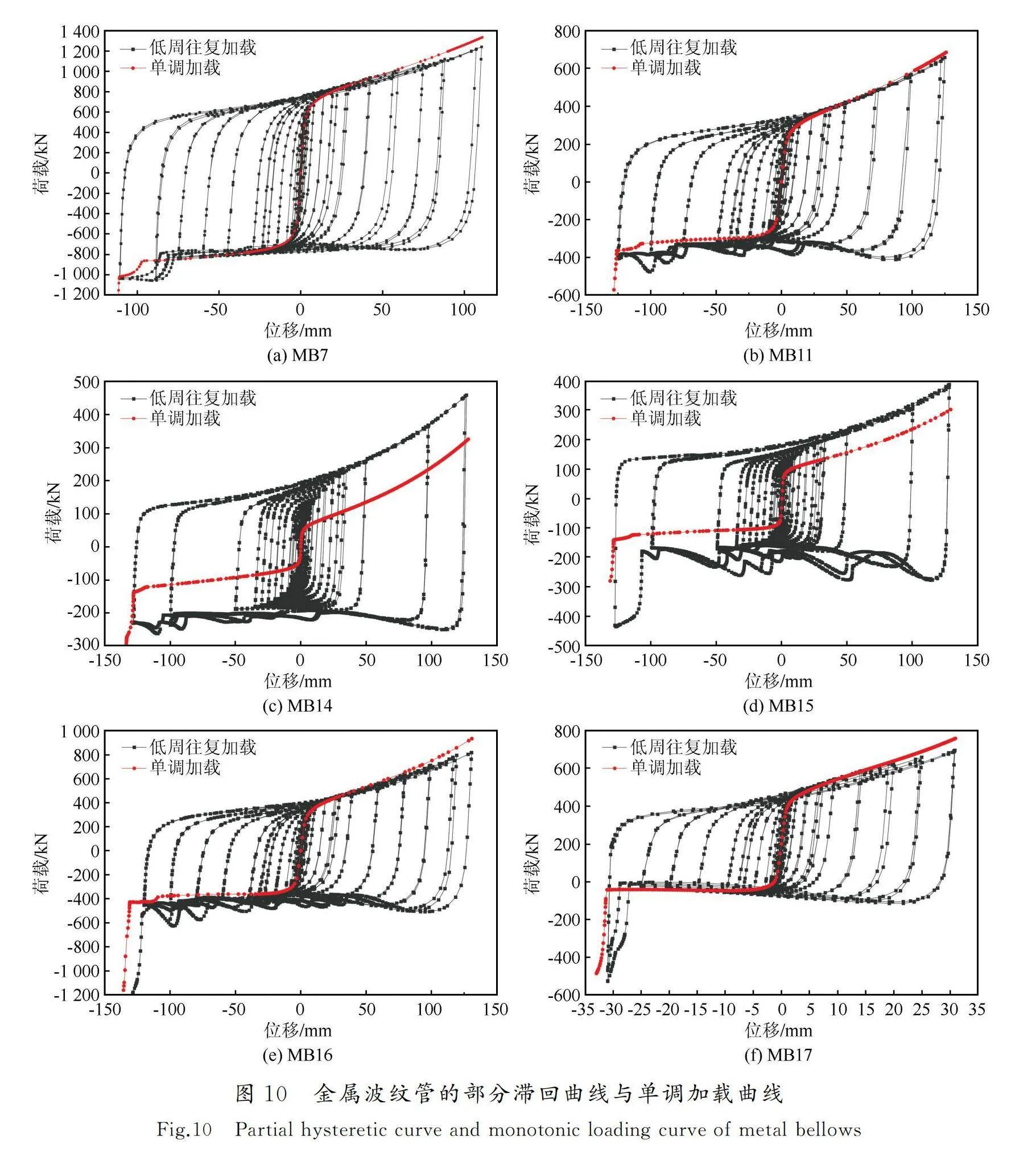
3.2 低周往復加載

金屬波紋管部分試件的有限元滯回曲線和單調加載曲線如圖10所示。由圖可知，滯回曲線均非常飽滿，幾乎沒有強度與剛度退化現象，且隨著波紋管壁厚的增加，滯回曲線的拉壓不等強現象明顯變弱。由于LYP100、LYP160兩種鋼材材料強化參數數值較大，試件MB14和MB15低周往復加載相比單調加載表現出較明顯的強化現象。其余牌號鋼材的試件，其骨架曲線與單調加載曲線幾乎完全重合。當位移較大時，大多數試件受壓階段的滯回曲線出現了“波動”現象。定義λ_d為波紋平均徑厚比，表示金屬波紋管的波紋平均直徑與壁厚的比值，即

λ_d=2r_m/t （13）

λ_d越大，波紋管滯回曲線“波動”現象越早且越明顯。隨著U型波紋直邊長度l的增加，波紋管“波動”現象略有降低。通過對19個試件滯回曲線的分析，建議λ_d不大于3.8。此外，在進行低周往復加載時，試件的邊波效應起始點及極限位移均略有降低，試件設計時，其最大工作位移應適當小于極限位移計算值，建議最大工作位移值不大于極限位移的0.8倍。在所有試件中，波紋平均徑厚比最小的試件MB7（λ_d=2.5），其拉壓不等強系數最小，約為1.3，與屈曲約束支撐相當;同時，MB7的滯回曲線非常飽滿，沒有出現“波動”現象，表現出較高的承載力，表明采用較小λ_d設計的波紋管，其力學性能更理想。

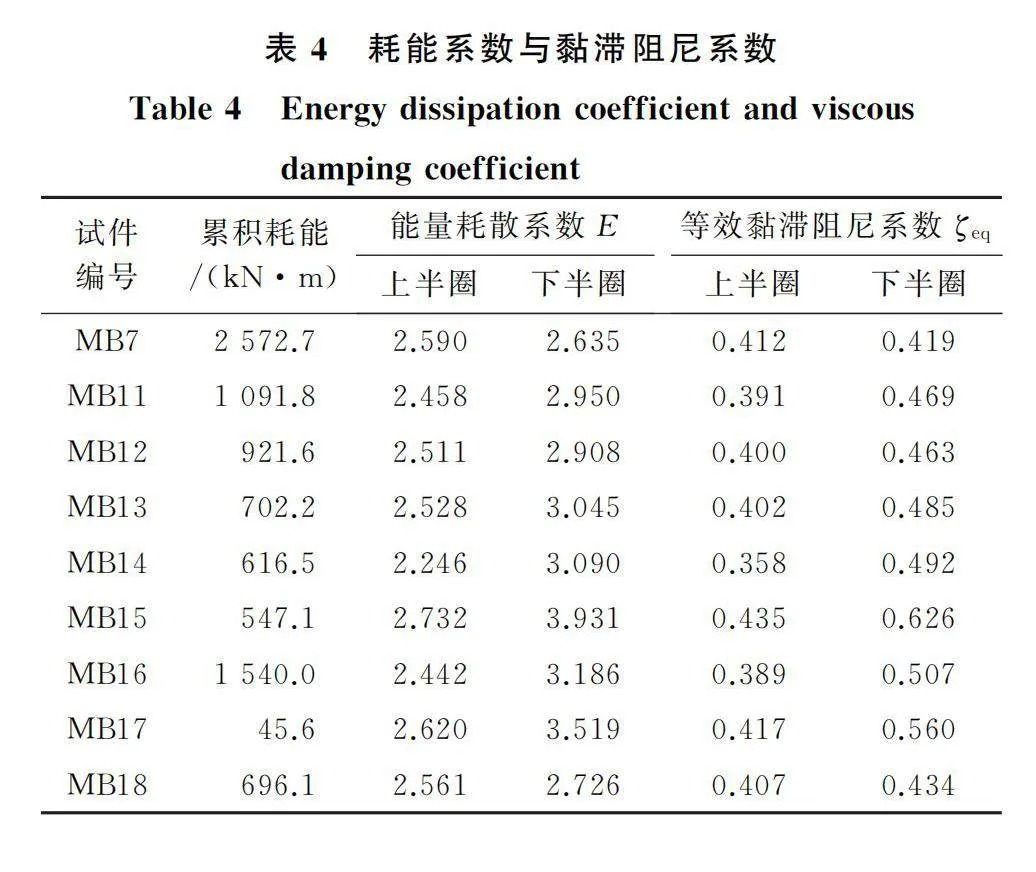
試件的能量耗散系數和等效黏滯阻尼系數可根據我國《建筑抗震試驗規程（JGJT 101—2015）》^［27］進行計算。計算所用滯回曲線取往復加載時極限位移前的最后一圈循環加載曲線，累積耗能為所有滯回曲線所圍成面積之和。表4給出了部分試件的能量耗散系數、等效黏滯阻尼系數和累積耗能情況，其余試件未在表中列出，是由于其強非線性導致有限元后期計算結果不收斂。從表中可以看出：各試件的等效黏滯阻尼系數和能量耗散系數都比較高;累積耗能與試件的波數、波紋管的壁厚及材料屈服強度等參數密切相關;壁厚12 mm的MB7試件累積耗能最大，達到2 572.7 kN·m;材料屈服強度最高的MB16試件累計耗能達到1 540.0 kN·m;波數只有1波的MB17試件累積耗能只有45.6 kN·m;采用低屈服點鋼材的MB14和BM15試件的累積耗能均不高。因此，較大壁厚、較多波數、較高強度鋼材的試件能獲得較大的累積耗能。

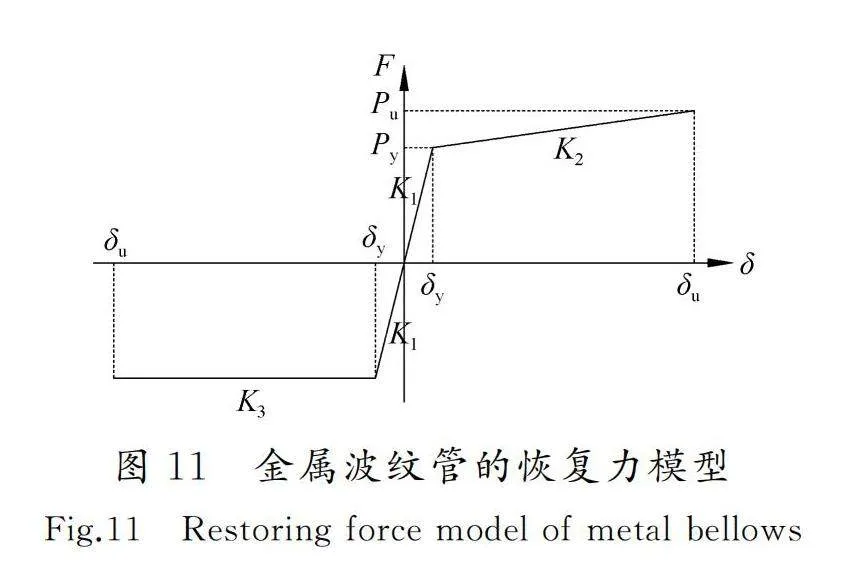
4 AUTMBD的恢復力模型

通過以上分析，得到金屬波紋管的恢復力模型如圖11所示。其關鍵力學指標為：第一剛度K₁、第二剛度K₂、第三剛度K₃、屈服荷載P_y、極限荷載P_u、屈服位移δ_y和極限位移δ_u。K₁為AUTMBD的彈性剛度，其值采用第2節中考慮邊波效應修正后的簡化分析方法計算得到。K₂為受拉屈服后剛度，其大小根據3.1節中受拉屈服后剛度與屈服前剛度比λ_k進行計算。K₃為受壓屈曲后剛度，按照3.1節分析結果可取為0。P_y為屈服荷載，按照第2節的簡化分析方法計算，同時采用考慮到邊波效應的修正系數λ_p進行修正。δ_y為屈服位移，可由K₁及P_y計算得到。δ_u為AUTMBD的極限位移（最大設計工作位移），應先按照3.1節中極限位移系數確定實際極限位移，再將實際極限位移的0.8倍取值為δ_u。P_u可根據P_y、K₂、δ_y及δ_u計算得到。

5 AUTMBD設計參數確定

AUTMBD的設計參數主要包括內徑D_b、壁厚t、波峰內徑r_ic（與波谷外徑r_ir相等）、波數n，波紋直邊長度l，及材料屈服強度f_y。這些參數的確定方法及過程如下：

（1） 確定材料屈服強度f_y

制作阻尼器的鋼材牌號確定后，其材料屈服強度隨之確定。一般來說，材料強度越高，阻尼器的承載力也越大，但強度越高的鋼材其塑性性能越差，從而會導致阻尼器提前破壞，因此，應盡可能選用強度較低的鋼材進行制作。建議采用鑄鋼工藝生產時，優先選用LYP100 或LYP160等低屈服點鋼材；采用機械加工生產時，由于目前市場上低屈服點鋼材多為板材，無法滿足機械加工需求，因此可選用Q235或20#鋼材。

（2） 確定工作位移δ_u

根據阻尼器在鋼框架結構中的安裝方式，按照幾何關系，取1/50的彈塑性層間位移角，計算AUTMBD的工作位移δ_u。

（3） 確定極限位移上限值δ_th

根據第4節及3.1節的分析結果，由δ_u=0.8δ_re和δ_re=λδ_th計算得到δ_th，λ為極限位移系數，可在0.6～0.8之間取值。

（4） 確定壁厚t

增加波紋管的壁厚t可顯著增加其承載能力。可根據AUTMBD在結構中的需求承載力先假定t值，然后按照式（7）進行承載力驗算。當阻尼器需求承載力較高時，可以假定一個較大的t值，反之亦然，但t值不宜小于3 mm。

（5） 確定波峰內徑r_ic

由3.2節可知，波紋平均徑厚比λ_d不宜大于3.8，即λ_d=2r_m/t=2（r_ic+t）/t=2r_ic/t+1≤3.8，從而r_ic/t≤1.4。根據上述假定的t值即可確定r_ic。

（6） 確定波數n

由前述已經確定的壁厚t、波峰內徑r_ic及極限位移上限值δ_th，根據δ_th=2n（2r_m-t）即可確定波數n。為了保證阻尼器的性能，波數n不宜小于3，同時為了使阻尼器在軸向荷載作用下不發生彎曲失穩，波數n不宜太大。由文獻［26］可知，波數n的取值應滿足L_b/D_b=nq/D_b=n（4r_ic+2t）/D_b≤3。

（7） 確定波紋管內徑D_b

波紋管外徑（記為D_B）應小于安裝位置處框架梁的寬度（記為B_b），即D_B=D_b+4r_ic+2l+4t≤B_b。確定D_b時，可根據梁寬B_b先按l=0確定一個初始值，然后按照式（7）、（8）進行承載力和剛度驗算。

（8） 確定波紋直邊長度l

根據文獻［26］，波高h應滿足2r_m≤h≤D_b/3，由此可得0≤l≤D_b/3-2r_ic-t。結合3.1節中的分析結果，可初步確定l值。

以上設計參數初步確定后應根據阻尼器的工程需求承載力、位移及剛度進行驗算，如驗算不通過則結合前述阻尼器參數化分析結果進行優化并重新驗算。

6 結論

本文提出了一種新型軸向拉壓式U型厚壁金屬波紋管阻尼器，該阻尼器依靠波紋段的多波屈曲進行耗能。通過理論分析及有限元參數化分析，建立了阻尼器的恢復力模型，研究了阻尼器不同幾何參數對其力學性能的影響，并得到以下結論：

（1） 該厚壁金屬波紋管阻尼器滯回曲線飽滿，等效黏滯阻尼系數與能量耗散系數較高，耗能能力強，其累積耗能能力與波紋管的壁厚、波數及材料的屈服強度成正比。

（2） 所提阻尼器在荷載作用下應盡量避免局部畸變屈曲，以獲得較優的力學性能，建議設計時波紋平均徑厚比不大于3.8，最大設計工作位移不大于實際極限位移的0.8倍。

（3） 修正后的簡化分析方法考慮了邊波效應的影響，總體上與有限元結果較為一致，與規范法相比具有更高的精度，為軸向拉壓式厚壁金屬波紋管阻尼器的設計提供了依據。

（4） 隨著壁厚的增加，阻尼器的剛度、屈服荷載、受壓屈服后剛度、受拉屈服后剛度、受壓極限荷載，及受拉極限荷載顯著增加，拉壓不等強系數則呈減小趨勢。多波與單波波紋管阻尼器相比，極限受拉承載力幾乎相等，但隨著波數的增加，極限位移及累積耗能顯著增加，受拉屈服后剛度隨著波數的增加而急劇降低。此外，由于邊波效應的影響，單波波紋管阻尼器的極限受壓承載力略低于多波波紋管阻尼器。

參考文獻（References）

［1］朱柏潔，張令心，王濤.軸力作用下剪切鋼板阻尼器力學性能試驗研究［J］.工程力學，2018，35（增刊1）：140-144.

ZHU Baijie，ZHANG Lingxin，WANG Tao.Tests on the mechanical behavior of steel shear panel dampers under axial loads［J］.Engineering Mechanics，2018，35（Suppl01）：140-144.

［2］李玉順，大井謙一，沈世釗.鋼框架結構軟鋼阻尼器振動控制的試驗及理論研究［J］.建筑結構學報，2004，25（2）：1-7，14.

LI Yushun，KENICHI Ohi，SHEN Shizhao.Experimental and theoretical study on vibration control of steel frame attached with hysteretic dampers［J］.Journal of Building Structures，2004，25（2）：1-7，14.

［3］陳云，蔣歡軍，劉濤，等.分級屈服型金屬阻尼器抗震性能研究［J］.工程力學，2019，36（3）：53-62.

CHEN Yun，JIANG Huanjun，LIU Tao，et al.Study on the seismic behavior of graded yielding metal dampers［J］.Engineering Mechanics，2019，36（3）：53-62.

［4］CHEN Y，CHEN C，JIANG H J，et al.Study of an innovative graded yield metal damper［J］.Journal of Constructional Steel Research，2019，160：240-254.

［5］FENG H，ZHOU F Y，ZHU H P.Proposing a butterfly-liked metallic damper for passive energy dissipation in structures［J］.Journal of Constructional Steel Research，2021，187：106962.

［6］ZHENG J，ZHANG C W，LI A Q.Experimental investigation on the mechanical properties of curved metallic plate dampers［J］.Applied Sciences，2019，10（1）：269.

［7］TAIYARI F，MAZZOLANI F M，BAGHERI S.A proposal for energy dissipative braces with U-shaped steel strips［J］.Journal of Constructional Steel Research，2019，154：110-122.

［8］DEMIR S，HUSEM M.Saw type seismic energy dissipaters：development and cyclic loading test［J］.Journal of Constructional Steel Research，2018，150：264-276.

［9］LOTFI MAHYARI S，TAJMIR RIAHI H，HASHEMI M.Investigating the analytical and experimental performance of a pure torsional yielding damper［J］.Journal of Constructional Steel Research，2019，161：385-399.

［10］鄧開來，潘鵬.變截面軟鋼剪切阻尼器試驗研究［J］.工程力學，2016，33（5）：82-88.

DENG Kailai，PAN Peng.Experimental study of steel shear panel dampers with varying cross-sections［J］.Engineering Mechanics，2016，33（5）：82-88.

［11］吳山，何浩祥，蘭炳稷，等.多階段屈服及失效型金屬套管阻尼器性能試驗及分析［J］.土木工程學報，2022，55（12）：36-46.

WU Shan，HE Haoxiang，LAN Bingji，et al.Experimental study and analysis on performance of metal tube damper with multi-stage yield and failure［J］.China Civil Engineering Journal，2022，55（12）：36-46.

［12］胡大柱，孫航，徐一鳴，等.軸向布置金屬阻尼器力學性能研究［J］.地震工程與工程振動，2021，41（1）：122-131.

HU Dazhu，SUN Hang，XU Yiming，et al.Study on mechanical properties of axial arrangement metal damper［J］.Earthquake Engineering and Engineering Dynamics，2021，41（1）：122-131.

［13］周云，盧德輝，張敏，等.鋼管鉛阻尼器滯回性能試驗研究［J］.建筑結構學報，2017，38（9）：102-109.

ZHOU Yun，LU Dehui，ZHANG Min，et al.Experimental investigation on hysteretic performance of lead-filled steel tube damper［J］.Journal of Building Structures，2017，38（9）：102-109.

［14］盧德輝，周云，鄧雪松，等.鋼管鉛阻尼器耗能機理研究［J］.土木工程學報，2016，49（12）：45-51.

LU Dehui，ZHOU Yun，DENG Xuesong，et al.Study on energy dissipation mechanism of lead-filled steel tube damper［J］.China Civil Engineering Journal，2016，49（12）：45-51.

［15］周云，盧德輝，張敏.鋼管鉛阻尼器的性能試驗研究［J］.土木工程學報，2017，50（1）：46-52.

ZHOU Yun，LU Dehui，ZHANG Min.Study on mechanical properties of lead-filled steel tube damper［J］.China Civil Engineering Journal，2017，50（1）：46-52.

［16］盧德輝，周云，鄧雪松，等.鋼管鉛阻尼器構造優化及模擬分析［J］.工程力學，2017，34（3）：76-83.

LU Dehui，ZHOU Yun，DENG Xuesong，et al.Optimization of configuration and finite element modeling for lead-filled steel tube dampers［J］.Engineering Mechanics，2017，34（3）：76-83.

［17］XIANG X M，LU G，LI Z X，et al.Finite element analysis and experimental study on a bellows joint［J］.Engineering Structures，2017，151：584-598.

［18］MOTAMEDI M，NATEGHI-A F.Study on mechanical characteristics of accordion metallic damper［J］.Journal of Constructional Steel Research，2018，142：68-77.

［19］邵鶴天，吳勝，周云.波紋鋼管鉛阻尼器構造與耗能機理分析研究［J］.工程抗震與加固改造，2022，44（1）：110-115，128.

SHAO Hetian，WU Sheng，ZHOU Yun.Study on the structure and energy dissipation mechanism of lead-filled corrugated steel tube damper［J］.Earthquake Resistant Engineering and Retrofitting，2022，44（1）：110-115，128.

［20］周云，吳勝.波紋鋼管鉛阻尼器耗能性能分析研究［J］.世界地震工程，2020，36（4）：103-111.

ZHOU Yun，WU Sheng.Energy dissipation performance analysis of lead-filled corrugated steel tube damper［J］.World Earthquake Engineering，2020，36（4）：103-111.

［21］黎廷新，胡堅，洪錫鋼.U形膨脹節的軸向位移應力和軸向剛度［J］.煉油設備設計，1981，2（3）：9-18.

LI Tingxin，HU Jian，HONG Xigang.Axial displacement stress and axial stiffness of U-shaped expansion joint［J］.Petrochemical Equipment Technology，1981，2（3）：9-18.

［22］王佼姣，石永久，王元清，等.低屈服點鋼材LYP100循環加載試驗［J］.浙江大學學報（工學版），2015，49（8）：1401-1409.

WANG Jiaojiao，SHI Yongjiu，WANG Yuanqing，et al.Experimental study on low yield point steel LYP100 under cyclic loading［J］.Journal of Zhejiang University （Engineering Science），2015，49（8）：1401-1409.

［23］王萌，錢鳳霞，楊維國.低屈服點LYP160鋼材本構關系研究［J］.建筑結構學報，2017，38（2）：55-62.

WANG Meng，QIAN Fengxia，YANG Weiguo.Constitutive behavior of low yield point steel LYP160［J］.Journal of Building Structures，2017，38（2）：55-62.

［24］王萌.強烈地震作用下鋼框架的損傷退化行為［D］.北京：清華大學，2013.

WANG Meng.Damage and degradation behaviors of steel frames under severe earthquake［D］.Beijing：Tsinghua University，2013.

［25］ATC-24.Guidelines for cyclic seismic testing of components of steel structures［S］.Redwood City：Applied Technology Council，1992.

［26］國家市場監督管理總局，國家標準化管理委員會.壓力容器波形膨脹節：GB/T 16749—2018［S］.北京：中國標準出版社，2018.

State Administration for Market Regulation，Standardization Administration of the People's Republic of China.Bellows expansion joints for pressure vessel：GB/T 16749—2018［S］.Beijing：Standards Press of China，2018.

［27］中華人民共和國住房和城鄉建設部.建筑抗震試驗規程：JGJ/T 101—2015［S］.北京：中國建筑工業出版社，2015.

Ministry of Housing and Urban-Rural Development of the People's Republic of China.Specification for seismic test of buildings：JGJ/T 101—2015［S］.Beijing：China Architecture amp; Building Press，2015.

（本文編輯：張向紅）