生問引學(xué)：學(xué)習(xí)真實(shí)發(fā)生，思維切實(shí)提升

竺柏明 童欣

［摘 要］人教版教材中的“分?jǐn)?shù)與除法”是憑借兩個“被除數(shù)小于除數(shù)”的例子歸納得出分?jǐn)?shù)與除法的關(guān)系，但學(xué)生對此可能會產(chǎn)生疑問。為了促進(jìn)學(xué)生深入思考，教師要鼓勵學(xué)生提出他們內(nèi)心的疑問，再借助疑問深入探究“被除數(shù)大于或等于除數(shù)”的情況。通過完全歸納的過程，學(xué)生能夠深刻地構(gòu)建知識體系，學(xué)習(xí)得以真實(shí)發(fā)生，思維得到切實(shí)提升。

［關(guān)鍵詞］分?jǐn)?shù)與除法；發(fā)現(xiàn)問題；提出問題；思維；推理

［中圖分類號］ G623.5［文獻(xiàn)標(biāo)識碼］ A［文章編號］ 1007-9068（2023）29-0002-04

【課前之思】

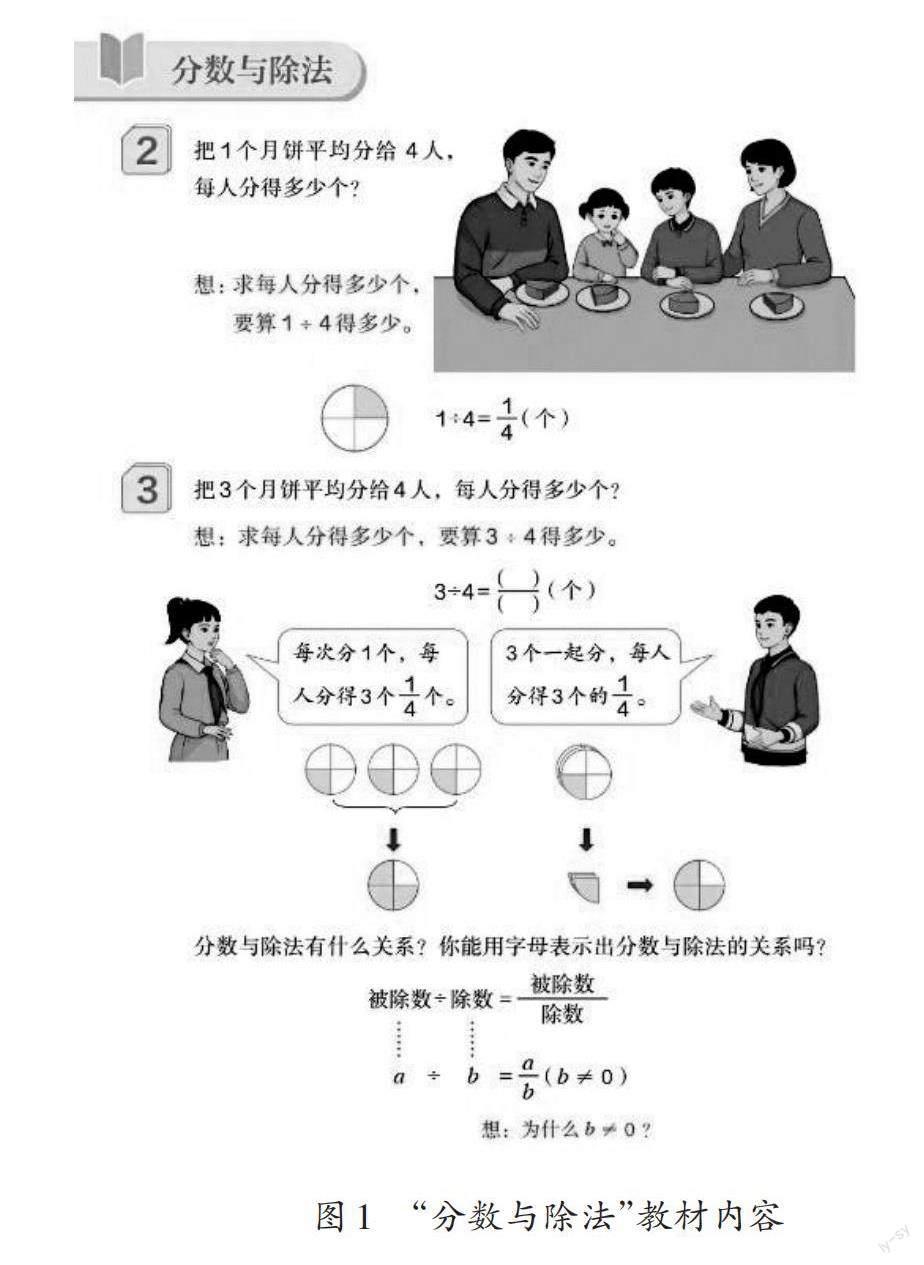
人教版教材將“分?jǐn)?shù)與除法”編排在五年級下冊。從教材呈現(xiàn)的內(nèi)容（如圖1）來看，本課是借助兩個關(guān)于除法的實(shí)際問題，揭示分?jǐn)?shù)與除法的關(guān)系，使學(xué)生不僅能理解分?jǐn)?shù)表示部分與整體的關(guān)系（即“份數(shù)”定義），還能理解分?jǐn)?shù)表示兩個整數(shù)相除的商（即“商”定義），從而深化和擴(kuò)展對分?jǐn)?shù)意義的理解。

教材以1÷4=?和3÷4=?兩道除法算式為例，得出分?jǐn)?shù)與除法的關(guān)系。然而，這種方法在邏輯上存在一些不足之處，因?yàn)樗鼉H考慮了被除數(shù)小于除數(shù)的情況，沒有涵蓋被除數(shù)大于或等于除數(shù)的情況。這種不完整的歸納可能會引發(fā)學(xué)生的疑問：“如果被除數(shù)大于除數(shù)，或者被除數(shù)和除數(shù)相等，會有什么結(jié)果呢？”需要指出的是，在之前的除法學(xué)習(xí)中，被除數(shù)大于除數(shù)的情況更為常見，因此，僅以不常見的被除數(shù)小于除數(shù)的情況來得出結(jié)論可能會引起學(xué)生的疑問。

根據(jù)新的課程理念，引導(dǎo)學(xué)生發(fā)現(xiàn)和提出有意義的數(shù)學(xué)問題是培養(yǎng)學(xué)生質(zhì)疑精神和批判性思維的重要方式，這也是值得追求的數(shù)學(xué)課程目標(biāo)。因此，筆者建議將學(xué)生提出的問題納入教學(xué)中，以激發(fā)學(xué)生深入探究和全面歸納的興趣。這將為他們提供發(fā)展推理意識的絕佳機(jī)會，而推理正是《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》（以下簡稱《課程標(biāo)準(zhǔn)》）所強(qiáng)調(diào)的最重要的數(shù)學(xué)思維之一。

也許有人會擔(dān)心，這樣的教學(xué)是否會涉及假分?jǐn)?shù)？（在人教版教材中，假分?jǐn)?shù)通常會在后面的課程中介紹，而不是通過兩數(shù)相除引入）筆者認(rèn)為這種擔(dān)憂是不必要的，因?yàn)椤墩n程標(biāo)準(zhǔn)》鼓勵教師“要整體分析數(shù)學(xué)內(nèi)容本質(zhì)和學(xué)生認(rèn)知規(guī)律，合理整合教學(xué)內(nèi)容”。假分?jǐn)?shù)的本質(zhì)是為了表示被除數(shù)大于除數(shù)時的商，而這節(jié)課正好介紹了兩個整數(shù)相除的商可以用分?jǐn)?shù)表示。因此，學(xué)生在學(xué)習(xí)過程中產(chǎn)生“被除數(shù)大于或等于除數(shù)時，商會如何表示”的疑問時，正是引入假分?jǐn)?shù)的合適時機(jī)。（北師大版教材采用了先教假分?jǐn)?shù)再教分?jǐn)?shù)和除法的關(guān)系的順序編排教學(xué)內(nèi)容）

根據(jù)以上思考，筆者進(jìn)行了多次嘗試，最終制訂了可行的教學(xué)方案。

【課堂實(shí)踐】

一、課題引思，明確方向

1.揭示課題，引發(fā)疑問

師：一起來讀一下課題。讀完課題，你有什么疑問？

生1：分?jǐn)?shù)是一種數(shù)，除法是一種運(yùn)算，它們有關(guān)系嗎？

生2：分?jǐn)?shù)怎么會與除法有關(guān)系呢？

師：今天我們就來研究它們的關(guān)系。

2.生成素材，初步感知

師（引導(dǎo)學(xué)生回憶學(xué)過的分?jǐn)?shù)和除法，并在黑板上寫下五六個例子）：你能發(fā)現(xiàn)哪個分?jǐn)?shù)與哪道除法有關(guān)系嗎？

生3：我發(fā)現(xiàn)1÷3和?有關(guān)系，它們是相等的。

師（板書：1÷3=?）：怎么解釋其中的道理？

生4：我可以用分餅來解釋。把1個餅平均分給3個人，每人就得?個餅。

師：對，把1個餅平均分給3個人，可以用除法算式1÷3，結(jié)果是多少呢？

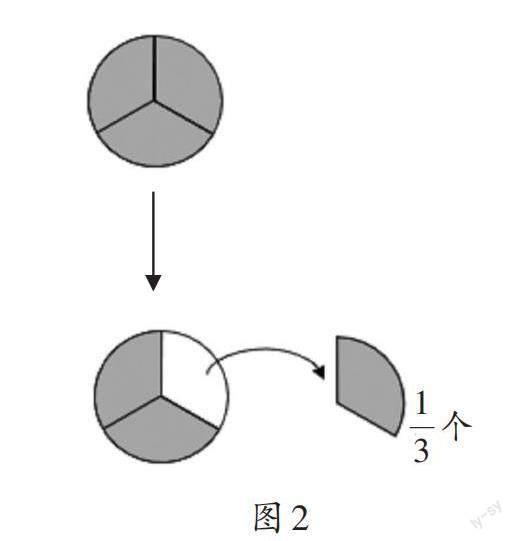
（教師邊說邊移動教具，并強(qiáng)調(diào)1個餅的?就是?個餅，如圖2）

[設(shè)計(jì)意圖：把課題作為學(xué)習(xí)素材，在適當(dāng)?shù)囊龑?dǎo)下，學(xué)生自然地產(chǎn)生疑問，產(chǎn)生探索知識的欲望。回顧舊知識能喚起學(xué)生對分?jǐn)?shù)基本含義的記憶，同時，使用教具引導(dǎo)學(xué)生認(rèn)識1個餅的?就是?個餅，這為后續(xù)學(xué)生的分析和表達(dá)打下堅(jiān)實(shí)基礎(chǔ)。]

二、逐層探究，自主釋問

1.加深感知，初步歸納

師：分?jǐn)?shù)與除法有什么關(guān)系呢？不著急，通過一個例子就下結(jié)論，太倉促了。我們繼續(xù)研究。如果把3個餅平均分給4個人，每人分到幾個餅？算式怎么列？它的商能用分?jǐn)?shù)表示嗎？在紙上畫一畫、寫一寫你的想法。

生1：把第一個餅平均分成4份，每人分到?個；把第二個餅平均分成4份，每人也分到?個；把第三個餅平均分成4份，每人也分到?個。一共是3個?個，所以每人分到的是?個餅。

生2：3個餅都平均分成4份，一共就是12份，平均分給4個人，每人分到3份，因?yàn)槊糠菔?個餅，所以3份就是?個餅。

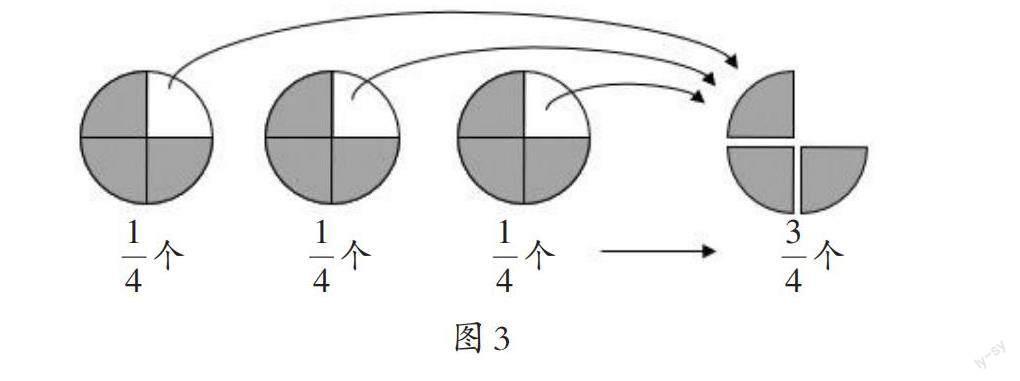
師：同學(xué)們的研究過程很精彩，雖然方法不同，但得到結(jié)果是一致的，也就是3÷4的商是?。我們可以用最基本的思路再來分析一遍。（出示圖3）

師：現(xiàn)在有兩個例子了。你覺得分?jǐn)?shù)與除法到底有什么關(guān)系？

生3：我發(fā)現(xiàn)被除數(shù)就是分?jǐn)?shù)里的分子，除數(shù)就是分?jǐn)?shù)里的分母。

師：你說的意思能用圖表示嗎？（引導(dǎo)學(xué)生在板書的算式中連線，如圖4）

師：好像的確如此！再試一個算式“2÷5”。

生4：2÷5等于?，把1個餅平均分成5份，每份是?個餅，2個?就是?。

[設(shè)計(jì)意圖：有了前面分餅的經(jīng)驗(yàn)，學(xué)生能比較順利地通過畫一畫、分一分來獨(dú)立研究3÷4的商。經(jīng)過教師引導(dǎo)，學(xué)生進(jìn)行了首次歸納，初步發(fā)現(xiàn)了分?jǐn)?shù)與除法的關(guān)系。]

2.觀察思考，提出問題

師：愛動腦筋的同學(xué)心里面一定產(chǎn)生了一些疑問吧！請說一說。

（給學(xué)生思考時間）

生5：被除數(shù)大于除數(shù)的除法還是這樣嗎？

生6：被除數(shù)等于除數(shù)的時候呢？

生7：整除的時候商也能用分?jǐn)?shù)表示嗎？

……

師：學(xué)習(xí)就是要這樣。在看似得到結(jié)論的時候，還能有質(zhì)疑的精神，能勇敢地提問，這不但需要智慧，還是一種了不起的能力。

[設(shè)計(jì)意圖：學(xué)生看似已經(jīng)歸納推理出了分?jǐn)?shù)與除法的關(guān)系，但不是很確定，更多的是簡單盲從或想當(dāng)然的心態(tài)。因此，教師在此處開啟一個提問的“窗口”， 鼓勵學(xué)生深入思考，從而發(fā)現(xiàn)問題并勇敢提出疑問，進(jìn)而形成批判性思維。]

3.再度探究，深刻感知

師：除法算式5÷4等于幾？

生8：等于[5/4]。

師：[5/4]的分子比分母大，你們是怎么理解5÷4=[5/4]的？

生9：把每個餅平均分成4份，每次拿?個餅，5次就是[5/4]個餅。

（因?yàn)槌霈F(xiàn)了分子比分母大的新情況，所以教師和學(xué)生一起借助教具將整個過程進(jìn)行梳理，如圖5所示）

生10：我的方法跟他的不一樣，5個餅平均分給4個人，可以每個人先分到1個，剩下的1個餅再平均分成4份，每人又得到?個，所以每個人就是1個還多?個。

師：雖然生10的分法不同，但結(jié)果和生9的是一樣的——1個餅里面有[4/4]個餅，再加?個餅，也就是[5/4]個。

（教師將1個餅補(bǔ)畫成[4/4]的樣子）

師：5÷4的商確實(shí)可以用[5/4]表示。看來被除數(shù)大于除數(shù)的時候，這樣的關(guān)系依然成立。再算算7÷3等于多少？

……

師：剛才有同學(xué)問“被除數(shù)等于除數(shù)的時候，這個算法是否成立”，誰來舉個例子說說看？

生11：5÷5。

師： 5÷5=5/5。5個?正好是1張餅，跟5除以5等于1一樣。

4.概括歸納，得到結(jié)論

師：我們已經(jīng)研究了很多例子，有被除數(shù)小于除數(shù)的，有被除數(shù)大于除數(shù)的，還有被除數(shù)等于除數(shù)的，三種不同的情況卻有相同的結(jié)論。對于分?jǐn)?shù)與除法的關(guān)系，你能用一個式子簡約地表示嗎？

生12：可以寫成“被除數(shù)÷除數(shù)=[被除數(shù)/除數(shù)]”。

師：也可以用字母表達(dá)，寫成[a÷b=a/b]，當(dāng)然，這里的[b]不能等于[0]。

[設(shè)計(jì)意圖：根據(jù)學(xué)生提出的問題，教師組織學(xué)生深度探究。學(xué)生通過研究被除數(shù)小于除數(shù)、被除數(shù)大于除數(shù)、被除數(shù)等于除數(shù)的除法與分?jǐn)?shù)之間的關(guān)系，將前面不完全歸納得出的結(jié)果依次進(jìn)行檢驗(yàn)，從而在完全歸納中得出結(jié)論，深刻地建構(gòu)了分?jǐn)?shù)與除法的關(guān)系，并切實(shí)地感受到了完全歸納思想方法的實(shí)用性。]

三、知識運(yùn)用，加深理解

1.鞏固練習(xí)，體會價值

師：我們歸納得出了分?jǐn)?shù)與除法的這個關(guān)系有什么用呢？一起來看大家之前寫的這些除法算式，它們的商分別是多少呢？

生1：20÷4[=20/4]，8÷3[=8/3]，113÷19[=113/19]。

師：看了這些結(jié)果，你有什么感受？

生2：用分?jǐn)?shù)表示除法的結(jié)果太簡單了！

師：兩個整數(shù)相除的商可以用分?jǐn)?shù)表示，那么你們之前所列舉的分?jǐn)?shù)，它們又分別是哪個除法算式的商呢？（學(xué)生回答略）

師：看見分?jǐn)?shù)就能想到除法，厲害！

[設(shè)計(jì)意圖：借助課前學(xué)生舉的除法和分?jǐn)?shù)的例子進(jìn)行練習(xí)，素材簡單，形式靈活，讓學(xué)生能夠很好地感受到所學(xué)知識的用途，感受到分?jǐn)?shù)的另一個來源。]

2.問題延伸，學(xué)法總結(jié)

師：你還有什么疑問嗎？

生3：被除數(shù)或除數(shù)是小數(shù)的時候也是這樣的關(guān)系嗎？

生4：分?jǐn)?shù)除法的時候也會這樣嗎？

……

師：這些問題又能引發(fā)我們進(jìn)一步思考。在學(xué)習(xí)中會提問太重要了，希望同學(xué)們能保持這樣的學(xué)習(xí)習(xí)慣。

【課后有感】

用以上思路執(zhí)教的“分?jǐn)?shù)與除法”不但讓人眼前一亮，課堂的效果也令人十分滿意。這節(jié)課的創(chuàng)新突破之處，主要就是“學(xué)生提問、以問引學(xué)”促成了學(xué)習(xí)的真實(shí)發(fā)生和思維的切實(shí)提升。

一、自主開展提問、釋問等活動，學(xué)習(xí)真實(shí)發(fā)生

整個課程可以看作是由學(xué)生的提問、釋問（即探究問題和解決問題）等活動串聯(lián)而成的。學(xué)生的提問分為三輪，每一輪的提問都是學(xué)生真實(shí)思考的表現(xiàn)，所提出的問題都激勵了學(xué)生主動地探究和解決問題，解決問題后又引發(fā)新的問題……學(xué)習(xí)在這樣的提問、釋問中真實(shí)發(fā)生，深入發(fā)展。例如，課堂一開始的提問激發(fā)了學(xué)生的學(xué)習(xí)興趣，學(xué)生明確了探究方向；探究兩個例題后，學(xué)生發(fā)現(xiàn)其中隱含的關(guān)系，此時提出更深入的問題，自主探究其他類型的除法，通過三種類型的除法，正式構(gòu)建了分?jǐn)?shù)與除法的關(guān)系，解決了之前的問題。學(xué)生自己提問、自己探究、自己解決問題，學(xué)習(xí)活動在學(xué)生獨(dú)立思考的基礎(chǔ)上展開。這樣的課堂讓學(xué)生興趣高漲，積極參與，學(xué)習(xí)活動生動而具有鮮明的特色。

二、充分經(jīng)歷完全歸納等過程，思維切實(shí)提升

本課的最大特色是將教材上的不完全歸納改為完全歸納，從而建立了分?jǐn)?shù)與除法的關(guān)系。這么做的原因是推理包括合情推理和演繹推理兩種，小學(xué)生主要接觸到的是合情推理中的不完全歸納推理。然而，隨著年齡的增長和理性思維的發(fā)展，學(xué)生在學(xué)習(xí)的過程中會產(chǎn)生疑問：“其他例子也是這樣嗎？”或“為什么都是這樣的呢？”這些疑問表明學(xué)生的思維已經(jīng)邁向了更高的水平。在這個時候引入演繹推理是適時的，它有助于學(xué)生思維水平的提升。

從本課可以看出，學(xué)生通過研究兩個除法算式來歸納出結(jié)論時，伴隨的是問題的出現(xiàn)，如“被除數(shù)大于除數(shù)和被除數(shù)等于除數(shù)的情況是否也是如此？”這類問題反映了學(xué)生思維的嚴(yán)謹(jǐn)性，學(xué)生渴望對問題進(jìn)行分類研究，從而實(shí)現(xiàn)完全歸納。在教師的引導(dǎo)下，學(xué)生經(jīng)歷了完全歸納的思維過程，從而豐富了對推理的體驗(yàn)（完全歸納推理是演繹推理的一種），邏輯思維和思考能力也得到了有效的鍛煉。

此外，學(xué)生在課堂中多次發(fā)現(xiàn)并提出有意義的數(shù)學(xué)問題，這也促進(jìn)了他們批判性思維和創(chuàng)造性思維的發(fā)展和鍛煉。這與《課程標(biāo)準(zhǔn)》的強(qiáng)調(diào)是一致的。

通過對這節(jié)課的研究，筆者再次認(rèn)識到，數(shù)學(xué)教學(xué)應(yīng)該抓住知識的育人價值，重視學(xué)生的學(xué)習(xí)心理，引導(dǎo)學(xué)生提出問題并自主探究，以問題為引導(dǎo)使學(xué)生更加主動和深入地學(xué)習(xí)。這種教學(xué)方法有助于學(xué)生更深刻地建構(gòu)知識，更有效地提升思維水平。

（責(zé)編 金 鈴）