土體類型差異對大跨度綜合管廊抗震性能影響

戎密仁, 馮超, 龐銀萍, 陳耀輝, 劉喜坤, 戎虎仁, 馬驍

1. 河北地質(zhì)大學(xué) a. 城市地質(zhì)與工程學(xué)院, b. 河北省地下人工環(huán)境智慧開發(fā)與管控技術(shù)創(chuàng)新中心, 河北 石家莊 050031; 2. 首爾科學(xué)綜合大學(xué)院大學(xué), 韓國 首爾 06983; 3. 河北雄安京翼質(zhì)量檢測服務(wù)有限公司, 河北 雄安 071700; 4. 山西大學(xué) 電力與建筑學(xué)院, 山西 太原 030006; 5. 大連交通大學(xué) 國際教育學(xué)院, 遼寧 大連 116028

0 引言

地下綜合管廊的抗震性能對其正常使用影響較大, 國內(nèi)學(xué)者針對這一問題進行廣泛, 并取得了顯著成果, 如: 史曉軍等[1]、 仉文崗等[2]、 魏奇科等[3]和陳守一等[4]基于相似理論, 利用振動臺試驗系統(tǒng),研究峰值加速度地震波作用下管廊各部位及周圍土體的動力響應(yīng), 得到不同PGA 作用下管廊各部件及周圍土體位移、 應(yīng)力分布規(guī)律; 岳慶霞[5]基于位移時程輸入法, 分析了地震波輸入方向、 人工邊界類型及土體—結(jié)構(gòu)作用面屬性差異對管廊動力響應(yīng)準確性影響; 研究者基于動力時程分析法, 分析了管廊破壞特征及非一致地震激勵下管廊動力響應(yīng)差異, 得到了土體—結(jié)構(gòu)相互作用面的分離、 滑移情況及管廊受力薄弱部位[6-8]; 部分學(xué)者研究了不同分析方法在管廊抗震分析中的適用性及精確度問題, 為管廊抗震相關(guān)工作的研究提供新思路[9,10]; 也有部分學(xué)者基于有限元理論, 研究不同地震波輸入方式作用下綜合管廊動力響應(yīng), 得到了綜合管廊動力響應(yīng)差異規(guī)律[11,12]; 王長祥[13]利用ABAQUS 軟件, 分析不同入射角度地震波作用下預(yù)制綜合管廊的整體抗震性能, 得到不同入射角度下管廊內(nèi)力、 位移分布規(guī)律; 王程[14]基于整體動力時程分析法, 研究管廊接縫張開量與地震波峰值加速度關(guān)系, 得到二維模型計算時張開量的折減系數(shù); 楊劍等[15]利用FLAC 軟件, 研究液化土體埋覆下綜合管廊抗震性動力響應(yīng), 得到土體液化后的加速度、 位移、 孔壓比等參數(shù)變化規(guī)律。

綜上所述, 研究者主要針對地震波類型差異、 不同方法差異對管廊的抗震性能影響進行研究, 而關(guān)于土體差異影響下管廊抗震性能變化方面的研究相對較少, 對大跨度綜合管廊的抗震性能分析少之又少; 然而, 土體性質(zhì)差異對于地下結(jié)構(gòu)的安全性、 耐久性影響較大, 且土體類型數(shù)量較多、 物理參數(shù)復(fù)雜, 不同土體對地震響應(yīng)程度不同, 易造成地下結(jié)構(gòu)各部位受力不均, 導(dǎo)致地下結(jié)構(gòu)破壞; 在地下綜合管廊工程中, 為了避免不同土體類型地震響應(yīng)差異造成的結(jié)構(gòu)坍塌、 內(nèi)部管道破裂等災(zāi)害, 對不同土體埋覆下綜合管廊的抗震性能研究就顯得極其重要、 迫切。 本文以濟南市水廠南路綜合管廊工程項目為依托, 通過動力時程分析法與有限元理論模擬研究相結(jié)合的方法, 系統(tǒng)研究不同土體對大跨度綜合管廊的抗震性能影響;該研究結(jié)果為國內(nèi)外大跨綜合管廊在抗震設(shè)計、 規(guī)劃與現(xiàn)場實施等方面提供指導(dǎo)。

1 工程背景與相關(guān)參數(shù)

1.1 大跨綜合管廊結(jié)構(gòu)

濟南市水廠南路綜合管廊全長1 617.864 m, 為綜合艙和電力艙組成的矩形雙艙結(jié)構(gòu)(圖1); 其中: 綜合艙凈寬4 000 mm、 凈高3 500 mm; 電力艙凈寬2 300 mm、凈高3 500 mm; 結(jié)構(gòu)地板、 頂板、 側(cè)壁厚度為500 mm、 中隔板厚300 mm, 均采用C35 混凝土澆筑,其混凝土參數(shù)如表1 所示; 上方覆土厚度為3 500 mm。

圖1 濟南水廠南路綜合管廊示意圖(mm)Fig.1 Schematic diagram of pipeline corridor of Shuichang South Road in Jinan City

表1 混凝土物理參數(shù)Table 1 Physical parameters of concrete

1.2 土體類型及力學(xué)參數(shù)

建設(shè)場地屬于第四系地貌單元, 為黃河沖積平原, 場地地勢較低, 地形較平坦; 主要由人工填土及洪積成因的粉土、 粉質(zhì)黏土及砂土組成(表2)。

表2 濟南市水廠南路巖土工程地質(zhì)評價Table 2 Geotechnical engineeringgeologl evaluation of Shuichang South Road in Jinan City

因人工填土的力學(xué)性能存在較大不確定、 且分布深度較淺, 對地下綜合管廊的受力影響較小; 本文僅對粉土、 粉質(zhì)黏土、 砂土埋覆下綜合管廊的抗震性能進行分析研究, 該區(qū)域的典型土體參數(shù)見表3[17]。

表3 土體物理參數(shù)Table 3 Physical parameters of soil

1.3 地震參數(shù)確定

該地處于齊河—廣饒斷裂帶、 桑梓店斷裂帶、 臥牛山斷裂帶影響范圍之內(nèi), 抗震設(shè)防烈度為VI 度,場地類別為III 類, 抗震設(shè)防烈度峰值加速度為0.1 g, 罕遇地震加速度為0.22 g[18], 地震動加速度反應(yīng)譜特征周期為0.65 s, 且無砂土液化現(xiàn)象。

2 大跨度綜合管廊抗震理論

2.1 土體—結(jié)構(gòu)相互作用確定分析

土體—結(jié)構(gòu)的相互作用對綜合管廊的動力響應(yīng)有重要影響, 由于土體與混凝土材料物理性質(zhì)差異性較大, 導(dǎo)致土體與管廊結(jié)構(gòu)之間接觸力學(xué)性質(zhì)較為復(fù)雜。 為確保理論模擬結(jié)果準確性, 擬采用接觸面力學(xué)分析法研究土體與管廊結(jié)構(gòu)二者之間的相互作用。

接觸面的力學(xué)關(guān)系通過定義主、 從面關(guān)系及接觸面屬性來實現(xiàn), 即: 當土體與結(jié)構(gòu)在相互作用面法線方向發(fā)生接觸時, 二者之間存在傳力關(guān)系, 反之則不存在; 同理, 當在相互作用面切線方向發(fā)生接觸時,可進行切向力的傳遞, 且切應(yīng)力τ大于極限切應(yīng)力τcrit時, 二者處于滑動狀態(tài), 反之則處于粘結(jié)狀態(tài);極限切應(yīng)力可表示為:

式中:p為法向力,μ為摩擦系數(shù)。

2.2 黏彈性邊界確定分析

為消除地震波的反射及低頻失穩(wěn)等影響, 在在動力分析模型的四周施加黏彈性邊界, 即在模型四周和底部設(shè)置黏彈性邊界—彈簧阻尼元件, 彈簧剛度及阻尼系數(shù)確定過程如下。

地震縱波波速:

地震橫波波速:

式中:λ為拉梅常數(shù);ν為泊松比, E 為彈性模量;ρ為土體密度。

彈簧法向剛度:

彈簧切向剛度:

法向阻尼系數(shù):

切向阻尼系數(shù):

式中:α為平面波與散射波幅值比, 通常取0.8;G為等效剪切模量;β為物理波速與視波速的比值,通常取1.1;A為邊界節(jié)點所代表的面積和, 取0.9;γ為結(jié)構(gòu)幾何中心到人工邊界點的距離[19,20]。

2.3 等效節(jié)點荷載分析

在反射波被完全吸收后, 可將振動問題轉(zhuǎn)化成四周及底部節(jié)點的自由場運動問題, 即地震波加速度荷載以等效節(jié)點力的形式施加在四周邊界節(jié)點上。 此時的等效節(jié)點力主要包括自由場位移計算、 地震波傳播速度計算及等效節(jié)點力計算3 部分, 節(jié)點應(yīng)力狀態(tài)與地震波速度及位移的函數(shù)關(guān)系可表示為:

式中:K為彈簧元件的剛度系數(shù),C為彈簧元件阻尼系數(shù),u為人工邊界節(jié)點處的位移向量,u·為人工邊界節(jié)點處的速度向量。 邊界節(jié)點的等效荷載為:

式中: A 為節(jié)點影響面積。

經(jīng)反射后的地震波到達地表時, 其三維場應(yīng)變可表示為:

當S 波入射時, 邊界節(jié)點任一時刻的位移及速度可表示為:

底面等效節(jié)點荷載可表示為(以底板下部為例,其他幾個面同理):

通過上式可將任一時刻地震波加速度轉(zhuǎn)化成模型四周各節(jié)點的節(jié)點力, 加速度時程曲線則轉(zhuǎn)化成各節(jié)點力隨時間變化的幅值曲線, 進而完成地震波加速度等效節(jié)點荷載的轉(zhuǎn)化, 可實現(xiàn)模型地震等效荷載的施加。

3 理論模型建立

3.1 地震波選取

選取埃爾森特羅N-S 方向地震波能量較為集中的前15 s 作為地震荷載, 進行分析計算并將峰值加速度調(diào)整為0.1 g, 以實現(xiàn)理論模擬濟南地區(qū)抗震設(shè)防烈度, 校正后的地震波加速度時程曲線如圖2 所示。

圖2 N-S 方向0.1g 地震波時程曲線Fig.2 Time history curve of 0.1g seismic wave in N-S direction

3.2 本構(gòu)模型選擇

為研究不同性質(zhì)土體差異對綜合管廊抗震性能的影響, 在建立理論模型時, 應(yīng)將土體和混凝土結(jié)構(gòu)的本構(gòu)模型分別考慮, 具體為: ①考慮選用黏彈性邊界進行了基本假設(shè), 在動力分析時的土體采用彈性本構(gòu)模型; ②分析管廊在地震荷載作用下的受力狀態(tài), 混凝土本構(gòu)模型采用塑性損傷模型(CDP 模型)。

3.3 土—結(jié)相互作用設(shè)置

為準確研究地震荷載作用下管廊結(jié)構(gòu)與周圍土體的滑移現(xiàn)象, 擬采用“表面與表面接觸” 方法實現(xiàn)管廊外表面與埋覆土體之間的接觸, 建立二者之間的相互作用關(guān)系。

將地下綜合管廊外表面設(shè)置為主表面, 與其接觸土體表面設(shè)置為從表面, 跟蹤方式選擇有限滑移方式; 將接觸面法向的接觸屬性定義為“硬” 接觸, 切向接觸屬性定義為“罰” 接觸, 摩擦系數(shù)取為1, 所得的土體—結(jié)構(gòu)接觸對如圖3 所示[16]。

圖3 土體—結(jié)構(gòu)相互作用接觸對Fig.3 Soil-structure interaction contact pair

3.4 地震波輸入及黏彈性邊界實現(xiàn)

在黏彈性邊界完全吸收反射波時, 地震波的輸入問題可轉(zhuǎn)化成邊界節(jié)點的自由場運動問題, 即將地震波加速度采用等效節(jié)點力的方式作用在模型邊界節(jié)點上; 具體黏彈性邊界及等效節(jié)點力的實現(xiàn)方式如下:

第一步: 對所要施加黏彈性邊界及等效節(jié)點荷載的模型外部邊界面施加大小為1 的均布荷載, 并約束其法線方向位移, 計算得到邊界節(jié)點影響面積及反力文件;

第二步: 提取邊界節(jié)點編號及坐標, 并將地震波加速度積分得到相應(yīng)的地震動速度及位移荷載文件;

第三步: 將地震波時間間隔、 模型尺寸、 土體彈性模量、 泊松、 密度等參數(shù)輸入到基于黏彈性邊界及地震動輸入理論編制的MATLAB 程序中, 計算得到荷載、 節(jié)點幅值及彈簧阻尼器單元文件, 最后導(dǎo)入inp文件實現(xiàn)黏彈性邊界及等效節(jié)點荷載的施加; 等效節(jié)點力、 黏彈性邊界實現(xiàn)分別如圖4、 圖5 所示。

圖4 地震加速度等效節(jié)點力Fig.4 Equivalent nodal forces of seismic

圖5 黏彈性邊界Fig.5 Viscoelastic boundary

3.5 大跨綜合管廊抗震性能研究工況

因剪切波(S 波) 對地下管廊結(jié)構(gòu)的抗震性能影響較大, 故在X 方向輸入地震波模擬S 波作用; 通過施加砂土、 粉土、 粉質(zhì)黏土等3 種埋覆土體, 來分析研究埋覆土體性質(zhì)差異對綜合管廊抗震性能影響, 進一步分析其相應(yīng)的位移、 加速度、 應(yīng)力響應(yīng)等參數(shù)。

4 抗震特性與機理分析

4.1 位移變化及機理研究

在管廊結(jié)構(gòu)頂部、 底部選取特征點, 得到相同地震荷載條件下, 砂土、 粉土、 粉質(zhì)黏土等3 種土體埋覆下結(jié)構(gòu)的位移變化特征和不同方向的位移時程曲線(圖6)。 分析可知: ①因地下管廊自身剛度較大, 在地震荷載下管廊自身變形較小; ②在S 波地震荷載作用下, 3 類土體埋覆下綜合管廊的位移時程曲線趨勢基本一致, 但不同方向的位移有所差異; 均在地震波輸入方向(X 向) 位移遠遠大于Y、 Z 方向的位移,且管頂位移均大于管底位移; ③粉土埋覆下綜合管廊的位移最大為0.145 m; 砂土埋覆下綜合管廊的位移最小為0.102 5 m。

圖6 不同土體埋覆下綜合管廊位移時程曲線Fig.6 Time history curve of displacement of comprehensive pipe gallery under different soil coverings

根據(jù)理論分析結(jié)果得到3 種不同土體埋覆下綜合管廊頂板、 底板的位移匯總表4。 分析可知: 砂土埋覆下綜合管廊的相對位移差與峰值位移規(guī)律相同, 其相對位移最小為2.774×10-4m, 粉土埋覆下綜合管廊的相對位移差最大為6.02×10-4m。

表4 綜合管廊頂板、 底板位移差Table 4 Displacement difference between roof and floor of pipe gallery

綜上分析可得出: ①3 種土體埋覆下地下綜合管廊頂板、 底板的峰值位移及位移差均隨土體彈性模量的增大而減小; ②在相同地震峰值加速度作用下, 隨埋覆土體彈性模量的增大, 土體的剛度也隨之增大,位移響應(yīng)隨之減小, 頂板與底板的位移差也逐漸減小; ③下部土體發(fā)生較大的位移變形, 比上部土體先發(fā)生破壞。

4.2 加速度響應(yīng)分析與機理研究

分析3 種不同土體埋覆下綜合管廊頂部與底部沿X 向的加速度時程曲線(圖7) 和加速度放大系數(shù)(表5) 可知:

表5 管廊頂板、 底板加速度放大系數(shù)Table 5 Acceleration amplification coefficient of roof and floor of pipe gallery

圖7 不同土體埋覆下綜合管廊加速度時程曲線Fig. 7 Time-history curve of acceleration of pipe gallery under different soil coverings

①隨土體彈性模量的增大, 結(jié)構(gòu)—土體相互作用振動頻率接近地震振動頻率, 造成加速度增大; ②管廊下部土體率先發(fā)生破壞, 地震波能量在傳播過程中耗能較大, 則管廊下部加速度小于頂部加速度; ③加速度和放大系數(shù)變化規(guī)律與位移響應(yīng)規(guī)律不同, 但整體上均隨土體彈性模量的增大而增大, 且管頂峰值加速度大于管底; ④砂土埋覆下綜合管廊峰值加速度放大系數(shù)最大為2.846, 粉土埋覆下綜合管廊加速度放大系數(shù)最小為1.271。

4.3 應(yīng)力響應(yīng)分析與機理研究

圖8、 圖9 分別表示3 種不同土體埋覆下綜合管廊頂板、 底板、 中隔板處X 方向的應(yīng)力時程曲線、 整體結(jié)構(gòu)應(yīng)力分布規(guī)律云圖, 分析可知: ①3 種不同土體埋覆下綜合管廊的應(yīng)力與加速度變化規(guī)律均相同,與埋覆土體的彈性模量呈正比, 中隔板應(yīng)力最大, 管頂應(yīng)力次之, 管底應(yīng)力最小; ②最大峰值應(yīng)力為0.12 MPa, 在砂土埋覆下中隔板位置處, 遠遠小于混凝土極限抗拉強度; ③3 種不同土體埋覆下管廊結(jié)構(gòu)的整體應(yīng)力分布規(guī)律一致。

圖8 不同土體埋覆下綜合管廊應(yīng)力時程曲線Fig.8 Time history curve of stress of pipe gallery under different soil coverings

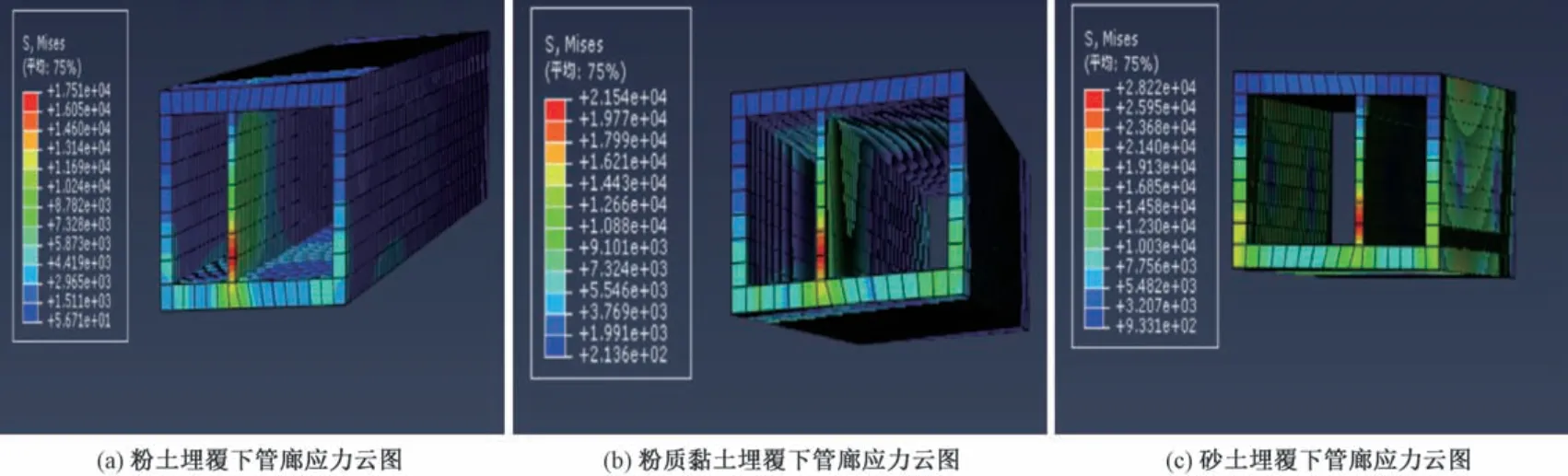
圖9 不同土體埋覆下綜合管廊應(yīng)力云圖Fig.9 Stress cloud diagram of pipe gallery under different soil coverings

5 結(jié)束語

基于黏彈性邊界理論和ABAQUS 有限元思想, 系統(tǒng)研究了砂土、 粉土、 粉質(zhì)黏土3 種不同類型土體埋覆下雙艙大跨綜合管廊結(jié)構(gòu)的抗震性能, 闡述了其力學(xué)特性與機理, 得到如下結(jié)論:

1) 研究并確定了大跨綜合管廊結(jié)構(gòu)中, 3 種覆土影響下管廊結(jié)構(gòu)抗震參數(shù); 在分析研究土體-結(jié)構(gòu)之間的相互作用機理、 黏彈性邊界、 地震波荷載施加等方面理論基礎(chǔ)之上, 提出了大跨綜合管廊的抗震理論, 明確了類似結(jié)構(gòu)的抗震分析研究理論。

2) 在3 種土體覆土下管廊結(jié)構(gòu)抗震理論, 研究并提出了理論模型中的地震波施加方式、 土體與管廊結(jié)構(gòu)的本構(gòu)模型與相互作用關(guān)系、 黏彈性邊界等關(guān)鍵性問題的實施方法。

3) 3 種不同土體埋覆下綜合管廊的位移以X 方向為主, 但隨土體彈性模量的增大而減小; 粉土埋覆下管廊結(jié)構(gòu)的位移最大為0.145 m, 位移差的最大值為0.602 mm; 砂土埋覆下綜合管廊結(jié)構(gòu)的加速度最大,且管頂加速度均大于管底加速度, 峰值最大為0.284 6 g; 最大應(yīng)力均在地震荷載輸入5 s 時, 管廊結(jié)構(gòu)中隔板處應(yīng)力大于底板、 頂板; 其峰值應(yīng)力為砂土埋覆下綜合管廊的中隔板板位置, 為0.12 MPa。