基于改進(jìn)Stacking與誤差修正的短期太陽(yáng)輻照度預(yù)測(cè)

王珊珊 吳霓 何嘉文 朱威

太陽(yáng)輻照度;光伏發(fā)電;Stacking算法;回歸預(yù)測(cè)算法;交叉驗(yàn)證

0 引言

太陽(yáng)能因其典型的波動(dòng)性與間歇性[1],造成光伏發(fā)電系統(tǒng)輸出功率的不穩(wěn)定性,對(duì)光伏發(fā)電并網(wǎng)與電網(wǎng)的安全穩(wěn)定運(yùn)行構(gòu)成巨大挑戰(zhàn)[2-3],同時(shí)也阻礙了大規(guī)模光伏發(fā)電并網(wǎng)．在光伏功率預(yù)測(cè)的眾多影響因素中,太陽(yáng)輻照度的影響是最直接、最顯著的,因此準(zhǔn)確的輻照度預(yù)測(cè)能夠提高光伏發(fā)電系統(tǒng)輸出功率的預(yù)測(cè)精度,有著重要的理論與應(yīng)用價(jià)值[4]．

近年來(lái),隨著機(jī)器學(xué)習(xí)技術(shù)的興起,國(guó)內(nèi)外許多學(xué)者將以SVR(Support Vector Regression)[5]、神經(jīng)網(wǎng)絡(luò)和隨機(jī)森林為代表的機(jī)器學(xué)習(xí)算法用于輻照度預(yù)測(cè)問(wèn)題中[6-8]．文獻(xiàn)[9]通過(guò)對(duì)9項(xiàng)氣象參數(shù)的不同組合作為輸入,對(duì)模型的預(yù)測(cè)精度進(jìn)行分析,提出一種基于非線性自回歸神經(jīng)網(wǎng)絡(luò)的輻照度預(yù)測(cè)模型,有效提高了預(yù)測(cè)精度．文獻(xiàn)[10]利用EMD(Empirical Mode Decomposition,EMD)和LMD(Local Mean Decomposition)將原始數(shù)據(jù)分解為多個(gè)分量序列,然后對(duì)各分量分別進(jìn)行LSSVM(Least Square Support Vector Machine)預(yù)測(cè),最后將各分量的預(yù)測(cè)結(jié)果進(jìn)行疊加得到最終預(yù)測(cè)值,相比LSSVM單獨(dú)預(yù)測(cè),精度有了明顯提升．單一的預(yù)測(cè)模型都是對(duì)特定假設(shè)空間進(jìn)行預(yù)測(cè),所以用單一模型來(lái)預(yù)測(cè)輻照度不可避免會(huì)存在預(yù)測(cè)誤差．而集成模型相比單一模型能夠集成多個(gè)模型的不同特點(diǎn),對(duì)各個(gè)模型取長(zhǎng)補(bǔ)短,從而提高預(yù)測(cè)性能,Stacking模型便是目前最熱門的集成模型之一．文獻(xiàn)[11]通過(guò)構(gòu)建一種基于同質(zhì)SVM(Support Vector Machine)弱學(xué)習(xí)器的Stacking模型,得到了比單一模型更精確的預(yù)測(cè)效果．文獻(xiàn)[12]提出一種新的向量表示法來(lái)穩(wěn)定模型數(shù)據(jù)維度,并根據(jù)預(yù)測(cè)精度來(lái)調(diào)整Stacking基模型賦權(quán),減少了輸出的噪聲和時(shí)間開(kāi)銷．目前大多研究專注于提升預(yù)測(cè)模型的精度來(lái)提高輻照度預(yù)測(cè)效果,卻忽略了模型的預(yù)測(cè)誤差中也存在非常多的有用信息,這導(dǎo)致現(xiàn)有研究難以進(jìn)一步提升短期輻照度預(yù)測(cè)的準(zhǔn)確度．

為了解決以上問(wèn)題,本文提出一種基于改進(jìn)Stacking集成學(xué)習(xí)與誤差修正的短期輻照度預(yù)測(cè)模型．在數(shù)據(jù)優(yōu)化層面,利用梯度提升決策樹(Gradient Boosting Decision Tree,GBDT)模型計(jì)算輻照度數(shù)據(jù)集各分量的重要度并排序,清除其中的冗余特征,提高預(yù)測(cè)精度和運(yùn)算效率．在算法創(chuàng)新方面,預(yù)測(cè)模型采用Stacking集成模型將4種差異性較大的算法融合,通過(guò)異質(zhì)集成得到優(yōu)于個(gè)體學(xué)習(xí)器的預(yù)測(cè)精度和泛化能力．針對(duì)Stacking模型平均處理測(cè)試集預(yù)測(cè)結(jié)果而帶來(lái)的掩蓋學(xué)習(xí)器優(yōu)劣的問(wèn)題,提出對(duì)初級(jí)層的輸出根據(jù)各模型的預(yù)測(cè)精度進(jìn)行加權(quán)處理．同時(shí),將Box-Cox變換嵌入Stacking,此舉可有效提高數(shù)據(jù)的正態(tài)性、可加性和同方差性．在誤差修正層面,針對(duì)Stacking模型的預(yù)測(cè)誤差構(gòu)建了基于隨機(jī)森林(Random Forest,RF)的輻照度誤差預(yù)測(cè)模型,并最終將改進(jìn)Stacking模型的預(yù)測(cè)結(jié)果與輻照度誤差預(yù)測(cè)結(jié)果進(jìn)行疊加以獲得最終預(yù)測(cè)結(jié)果．實(shí)驗(yàn)結(jié)果表明,該集成模型具有優(yōu)于單一模型和傳統(tǒng)Stacking模型的預(yù)測(cè)精度．

1 相關(guān)理論和方法

1.1 GBDT算法

GBDT是一種由多個(gè)弱學(xué)習(xí)器組成的迭代決策樹算法．該方法利用梯度增強(qiáng)算法來(lái)最小化損失函數(shù),達(dá)到逼近真實(shí)值的目的,具有靈活性高、魯棒性強(qiáng)、預(yù)測(cè)精度高等特點(diǎn)．

將GBDT應(yīng)用到特征重要度計(jì)算中,通過(guò)對(duì)決策樹中分裂節(jié)點(diǎn)增益進(jìn)行計(jì)算并積累求和,從而對(duì)某個(gè)特征進(jìn)行重要度評(píng)價(jià)．其中,特征j的全局重要性是以特征重要度平均值來(lái)度量的,其計(jì)算公式為

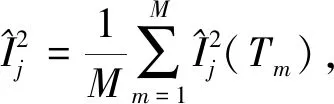
(1)

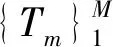
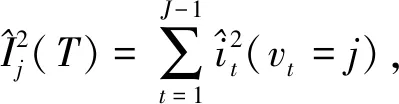
(2)

1.2 RF隨機(jī)森林

隨機(jī)森林[13]是一種基于決策樹的集成式機(jī)器學(xué)習(xí)算法,它在每一棵回歸樹建立隨機(jī)采樣樣本空間與特征空間,隨機(jī)屬性的引入減少了回歸樹模型間的相關(guān)關(guān)系,通過(guò)結(jié)合大量回歸樹來(lái)提高模型泛化能力,從而使算法具有效率高、精度高的特點(diǎn)．

1.3 Box-Cox變換

Box-Cox變換是一種基于極大似然估計(jì)的數(shù)據(jù)變換技術(shù),計(jì)算過(guò)程簡(jiǎn)單且無(wú)需先驗(yàn)信息,能夠有效提升觀測(cè)的同方差性、正態(tài)性和可加性[14]．

Box-Cox變換一般形式如下:

(3)

式中,λ為變換參數(shù),y為原始因變量,y(λ)為新變量,Box-Cox逆變換為

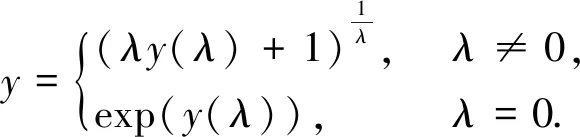
(4)

參數(shù)λ采用最大似然估計(jì)進(jìn)行計(jì)算,構(gòu)造似然函數(shù)L*(λ)如下:

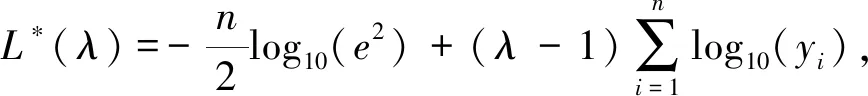
(5)

式中,n表示采樣次數(shù),e2表示y(λ)方差的極大似然估計(jì)值,通過(guò)式(5)求解出使得L*(λ)取最大值的最優(yōu)λ,利用該參數(shù)進(jìn)行Box-Cox變換可以很大程度上提升數(shù)據(jù)的正態(tài)性和數(shù)據(jù)間的相關(guān)性．

1.4 其他模型

1)K最鄰近算法(KNN)原理

K最鄰近算法(k-Nearest Neighbor,KNN)作為一種經(jīng)典的機(jī)器學(xué)習(xí)算法在理論上十分完善,具有算法簡(jiǎn)單、容易實(shí)現(xiàn)、訓(xùn)練效率高、對(duì)異常值不敏感等特點(diǎn)．該算法核心思想是對(duì)不同特征值之間的距離進(jìn)行度量,通常采用歐式距離和曼哈頓距離．

2)XGBoost算法

XGBoost(eXtreme Gradient Boosting)算法是基于GBDT算法改進(jìn)而來(lái)的,它通過(guò)增加正則項(xiàng)控制模型計(jì)算復(fù)雜度,并利用二階泰勒展開(kāi)式并行計(jì)算特征分裂增益以提高模型預(yù)測(cè)精度、減少計(jì)算時(shí)間．

3)支持向量回歸機(jī)(SVR)原理

支持向量機(jī)應(yīng)用于回歸問(wèn)題形成了SVR,輸入向量按照既定非線性映射映射至高維特征空間進(jìn)行線性回歸以獲得空間內(nèi)非線性回歸的效果．在回歸運(yùn)算時(shí),將不敏感損失函數(shù)引入到構(gòu)造中,以搜索到最優(yōu)的分類面使得訓(xùn)練樣本和該分類面之間的綜合誤差達(dá)到最小值．支持向量回歸在小樣本、高維、復(fù)雜數(shù)據(jù)上進(jìn)行非線性回歸預(yù)測(cè)時(shí)展現(xiàn)出了優(yōu)異的性能．

4)嶺回歸原理

嶺回歸(Ridge Regression)是一種正則化方法,通過(guò)舍棄最小二乘的無(wú)偏性和部分精確度,獲得了效果更好且回歸系數(shù)更符合實(shí)際的回歸過(guò)程．嶺回歸通過(guò)對(duì)損失函數(shù)增加懲罰項(xiàng)以控制線性模型復(fù)雜程度,增強(qiáng)了模型的穩(wěn)健性．

2 基于Box-Cox變換的改進(jìn)Stacking短期輻照度預(yù)測(cè)方法

2.1 Stacking集成學(xué)習(xí)模型

Stacking算法是一種分層集成的方法．不同于Bagging和Boosting算法整合同類型模型,Stacking算法能夠集成異質(zhì)模型[15]．在 Stacking 集成模型(圖1)的訓(xùn)練過(guò)程中,通常使用K折交叉驗(yàn)證法來(lái)劃分?jǐn)?shù)據(jù)集和進(jìn)行模型訓(xùn)練,以減少過(guò)擬合的風(fēng)險(xiǎn)．首先將原始數(shù)據(jù)集以8∶2的比例劃分為訓(xùn)練集和測(cè)試集,接著將訓(xùn)練集等分地劃分為k個(gè)子集,分別選擇其中k-1個(gè)子集的并集作為訓(xùn)練集,余下的1個(gè)子集作為驗(yàn)證集,由此可獲得k組訓(xùn)練集和驗(yàn)證集．對(duì)每個(gè)基模型都采用這k組訓(xùn)練集和驗(yàn)證集進(jìn)行學(xué)習(xí)器的訓(xùn)練和驗(yàn)證,并將預(yù)測(cè)結(jié)果配合樣本真實(shí)值標(biāo)簽構(gòu)造為新的訓(xùn)練集輸入第二層元學(xué)習(xí)器訓(xùn)練,最終得到的預(yù)測(cè)結(jié)果即為Stacking模型的最終預(yù)測(cè)結(jié)果．Stacking算法最突出的優(yōu)勢(shì)是集不同模型之長(zhǎng),能夠?qū)υ紨?shù)據(jù)進(jìn)行多角度的分析,使得模型獲得相比基模型更好的預(yù)測(cè)性能．所以基學(xué)習(xí)器應(yīng)選擇性能優(yōu)越且原理各異的模型,元學(xué)習(xí)器則應(yīng)選擇泛化能力強(qiáng)的算法,以融合各基學(xué)習(xí)器預(yù)測(cè)的優(yōu)點(diǎn),達(dá)到最優(yōu)的預(yù)測(cè)效果．本文選擇 SVR、XGBoost、KNN、嶺回歸作為基學(xué)習(xí)器,元學(xué)習(xí)器則使用泛化能力較強(qiáng)的嶺回歸算法．

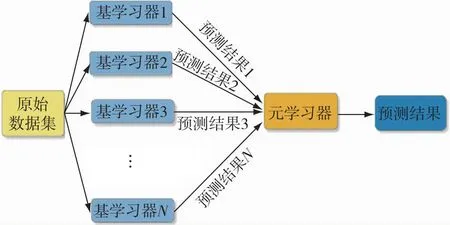
圖1 Stacking模型結(jié)構(gòu)Fig.1 Stacking model structure

2.2 改進(jìn)Stacking

2.2.1 基于GBDT算法的特征篩選

利用GBDT對(duì)輻照度數(shù)據(jù)進(jìn)行特征選擇,對(duì)各個(gè)特征進(jìn)行重要度排序．各特征與實(shí)際輻照度之間的相關(guān)系數(shù)如表1所示．由表1的相關(guān)系數(shù)數(shù)據(jù),剔除掉風(fēng)向、氣壓2個(gè)相關(guān)性弱的特征,最終選擇溫度、時(shí)刻、風(fēng)速、濕度作為模型輸入,降低計(jì)算復(fù)雜度,提升模型訓(xùn)練效率．

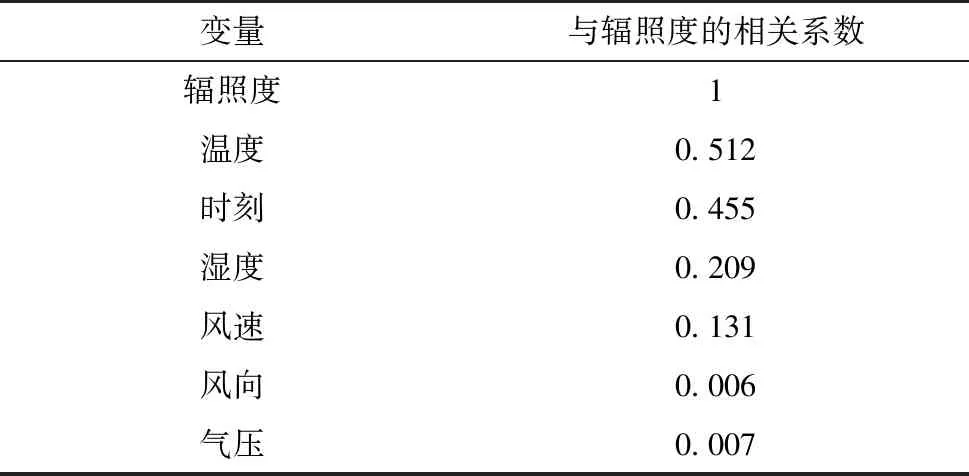
表1 相關(guān)系數(shù)

2.2.2 基模型賦權(quán)與Box-Cox變換

Stacking算法中元學(xué)習(xí)器輸入向量來(lái)自基學(xué)習(xí)器的輸出,使得訓(xùn)練數(shù)據(jù)被各層學(xué)習(xí)器重復(fù)學(xué)習(xí),造成模型的嚴(yán)重過(guò)擬合．因而需要在模型建立前對(duì)數(shù)據(jù)進(jìn)行交叉驗(yàn)證劃分,提升模型的泛化能力[16]．如果訓(xùn)練得到的基學(xué)習(xí)器模型預(yù)測(cè)效果比較好,那么該模型的預(yù)測(cè)結(jié)果也會(huì)更接近真實(shí)值．但傳統(tǒng)的Stacking模型初級(jí)層對(duì)測(cè)試集預(yù)測(cè)結(jié)果的處理方式為直接平均處理,使得優(yōu)秀模型的優(yōu)越性被其他模型掩蓋．同理,效果較差的模型也會(huì)因與其他模型平均而掩蓋其預(yù)測(cè)性能的不足．因此,本文針對(duì)同一基學(xué)習(xí)器在每折上訓(xùn)練得到的不同預(yù)測(cè)模型,依據(jù)其驗(yàn)證集預(yù)測(cè)值和真實(shí)值之間的誤差求得權(quán)值,再給測(cè)試集對(duì)同一種基模型的不同預(yù)測(cè)結(jié)果賦權(quán)．設(shè)學(xué)習(xí)器所訓(xùn)練出的模型預(yù)測(cè)誤差為eit(i=1,…,k),以此誤差在e1t,e2t,…,ekt精度總和中所占比例來(lái)分別確定權(quán)值ρ1,ρ2,…,ρk,然后對(duì)測(cè)試集的輸出結(jié)果賦權(quán),可以使精度更高的預(yù)測(cè)模型發(fā)揮其優(yōu)越性,增大其對(duì)最終結(jié)果的影響,并降低精度較低的模型對(duì)最終輸出的影響．

針對(duì)數(shù)據(jù)特征與輻照度數(shù)值相關(guān)程度不高的問(wèn)題,本文對(duì)第一層輸入第二層的訓(xùn)練集進(jìn)行Box-Cox變換處理,此舉可提高訓(xùn)練集的正態(tài)性和可預(yù)測(cè)性,提升各個(gè)特征與輻照度數(shù)據(jù)的內(nèi)在聯(lián)系,進(jìn)一步減小預(yù)測(cè)誤差．經(jīng)過(guò)Box-Cox變換后的訓(xùn)練集輸入元學(xué)習(xí)器,訓(xùn)練完成后用此學(xué)習(xí)器輸入經(jīng)加權(quán)處理后的測(cè)試集進(jìn)行預(yù)測(cè),得到預(yù)測(cè)結(jié)果．精度加權(quán)改進(jìn)和Box-Cox預(yù)處理流程如圖2所示．

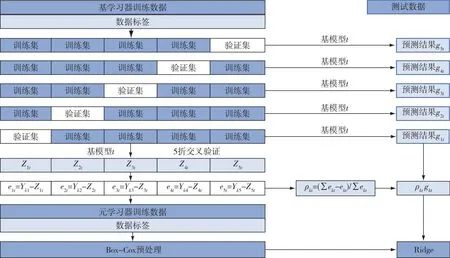
圖2 精度加權(quán)改進(jìn)和Box-Cox預(yù)處理Fig.2 Accuracy-weighted improvement and Box-Cox preprocessing

精度加權(quán)和Box-Cox改進(jìn)后的Stacking預(yù)測(cè)模型的流程如算法1所示.

2.2.3 基于RF模型的誤差修正方法

通過(guò)RF模型來(lái)尋找輻照度預(yù)測(cè)系統(tǒng)誤差的變化規(guī)律,有助于發(fā)現(xiàn)提高模型效果的有益規(guī)律,達(dá)到提升預(yù)測(cè)精度的目的．

輻照度預(yù)測(cè)誤差:

e=p′-p,

(6)

式中,e表示輻照度預(yù)測(cè)誤差,p′表示輻照度預(yù)測(cè)值,p表示輻照度真實(shí)值．

算法1:基于Box-Cox的改進(jìn)Stacking模型Input:訓(xùn)練集 D={(x1,y1),(x2,y2),…,(xk,yk)}1for t=1,2,…,T do2for i=1,2,…,k do3第零層第t個(gè)同質(zhì)基學(xué)習(xí)器k次訓(xùn)練學(xué)習(xí):{Zit=ht(xm,ym),i=1,…,k,t=1,…,T}→{Z1t,Z2t,…,Zkt}4第零層第T個(gè)異質(zhì)基學(xué)習(xí)器學(xué)習(xí)訓(xùn)練并構(gòu)成新的數(shù)據(jù)樣本:{Zit=ht(xm,ym),i=1,…,k,t=1,…,T}→{(Z11,Zk1),…,(Z1Tt,…,ZkT)}5構(gòu)成新的數(shù)據(jù)據(jù)樣本:Dnew={((Z11,…,Zk1),…,(Z1T,…,ZkT),ym)}6對(duì)新數(shù)據(jù)樣本作Box-Cox變換處理后輸入第一層7第一層預(yù)測(cè)算法δ訓(xùn)練得到模型:H=δ((Z11,…,Zk1),…,(Z1T,…,ZkT))8計(jì)算第零層同質(zhì)基學(xué)習(xí)器的誤差:{[(y1,y2,…,yk),…,(y1,y2,…,yk)]-[(Z11,Z21,…,Zk1),…,(Z1T,Z2T,…,ZkT)]}=9{[(e11,e21,…,ek1),…,(e1T,e2T,…,ekT)]}10權(quán)重計(jì)算:ρ11=(e21+…+ek1)/(e11+e21+…+ek1)?ρk1=(e11+…+ek-1,1)/(e11+e21+…+ek1)?ρkT=(e1T+…+ek-1,T)/(e1T+e2T+…+ekT)11對(duì)第零層測(cè)試集數(shù)據(jù)輸出進(jìn)行權(quán)重分配:(ρ11g11,ρ21g21,…,ρk1gk1)(ρ12g12,ρ22g22,…,ρk2gk2)?(ρ1Tg1T,ρ2Tg2T,…,ρkTgkT)12end13end

計(jì)算輻照度初步預(yù)測(cè)值p′與實(shí)際值p誤差e,將其作為校正因子,將輻照度校正的補(bǔ)償值e添加到預(yù)測(cè)值p′中,獲得校正后的輻照度預(yù)測(cè)值．

2.2.4 改進(jìn)Stacking模型總體流程

基于上述的GBDT算法、基模型賦權(quán)與Box-Cox變換、RF誤差修正,本文搭建了短期輻照度預(yù)測(cè)模型,如圖3所示．

圖3 基于改進(jìn)Stacking與誤差修正預(yù)測(cè)模型流程Fig.3 Prediction process based on improved Stacking with error correction

具體思路如下:

1)利用GBDT算法對(duì)輻照度原始數(shù)據(jù)進(jìn)行特征篩選,去除掉相關(guān)程度較低的冗余特征后,其余數(shù)據(jù)輸入改進(jìn)Stacking模型．

2)采用XGboost、SVR、嶺回歸、KNN作為Stacking的基學(xué)習(xí)器,嶺回歸作為元學(xué)習(xí)器．對(duì)于同一基學(xué)習(xí)器用不同樣本進(jìn)行訓(xùn)練,基學(xué)習(xí)器訓(xùn)練出的模型對(duì)驗(yàn)證集的預(yù)測(cè)誤差為eit(i=1,…,k),以此誤差在e1t,e2t,…,ekt精度總和之中所占比值來(lái)確定權(quán)值ρ1,ρ2,…,ρk,然后對(duì)第一層輸入第二層測(cè)試集的輸出結(jié)果進(jìn)行賦權(quán)．

3)對(duì)第一層輸入第二層的訓(xùn)練集進(jìn)行Box-Cox變換來(lái)提高訓(xùn)練集的正態(tài)性和可預(yù)測(cè)性．

4)經(jīng)過(guò)Box-Cox變換處理的訓(xùn)練集輸入元學(xué)習(xí)器,訓(xùn)練完畢之后,用此學(xué)習(xí)器對(duì)加權(quán)過(guò)后的測(cè)試集進(jìn)行預(yù)測(cè),得到預(yù)測(cè)結(jié)果．

5)采用上述模型進(jìn)行初步預(yù)測(cè)后,將初步預(yù)測(cè)的誤差數(shù)據(jù)輸入RF模型中訓(xùn)練,由此獲得誤差分布模型．將初步預(yù)測(cè)結(jié)果與誤差預(yù)測(cè)值進(jìn)行疊加得到最終預(yù)測(cè)結(jié)果．RF誤差修正模型可以有效彌補(bǔ)初步預(yù)測(cè)模型本身存在的誤差,進(jìn)一步提高預(yù)測(cè)的準(zhǔn)確度．

3 算例分析

3.1 數(shù)據(jù)選取

為驗(yàn)證本文模型對(duì)于短期輻照度預(yù)測(cè)的有效性,將中國(guó)北方某光伏電站作為具體研究對(duì)象．選取2017年2月1日至2018年1月31日的輻照度數(shù)據(jù)作為原始數(shù)據(jù)集,共2 920個(gè)樣本數(shù)據(jù)．輻照度數(shù)值采用太陽(yáng)總輻射量,采樣間隔為3 h,每日采樣8個(gè)點(diǎn),包括地表太陽(yáng)輻照度和風(fēng)速、風(fēng)向、溫度、濕度、氣壓共5項(xiàng)觀測(cè)指標(biāo)．將數(shù)據(jù)集按8∶2劃分,前80%的數(shù)據(jù)作為訓(xùn)練集,后20%數(shù)據(jù)作為測(cè)試集,進(jìn)行回歸預(yù)測(cè)．

3.2 模型評(píng)價(jià)指標(biāo)

本文選取均方根誤差(ERMSE)、平均絕對(duì)誤差(EMAE)和決定系數(shù)(R2)作為輻照度預(yù)測(cè)模型的效果評(píng)價(jià)指標(biāo),其中:R2用來(lái)檢驗(yàn)?zāi)Ｐ偷臄M合度,R2越大表明模型擬合程度越好;MAE、RMSE則用來(lái)檢驗(yàn)預(yù)測(cè)模型的精度,它們值越小說(shuō)明精度越高．具體的計(jì)算公式如下:

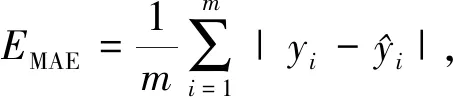
(7)

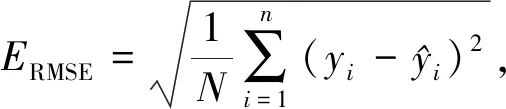
(8)

(9)

3.3 仿真實(shí)驗(yàn)及結(jié)果分析

首先,設(shè)計(jì)第一組實(shí)驗(yàn),對(duì)比Stacking模型與其各個(gè)基模型在輻照度短期預(yù)測(cè)上的性能,各模型預(yù)測(cè)值與輻照度實(shí)際值的橫向?qū)Ρ冉Y(jié)果如圖4所示,各模型的絕對(duì)誤差如圖5所示,各模型的評(píng)價(jià)指標(biāo)值如表2所示．

表2 不同模型的評(píng)價(jià)指標(biāo)

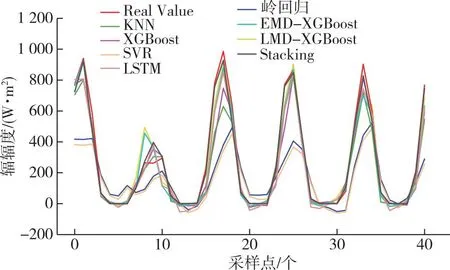
圖4 不同模型預(yù)測(cè)結(jié)果對(duì)比Fig.4 Prediction result comparison between Stacking method and traditional models

圖5 不同模型的預(yù)測(cè)誤差對(duì)比Fig.5 Prediction error comparison between Stacking method and traditional models

由圖4、5和表2分析可知:Stacking模型相較于其基模型中的單一模型KNN、SVR和嶺回歸,R2分別提升0.118、0.424和0.504,與深度學(xué)習(xí)模型LSTM相比,R2指標(biāo)提升0.101;將EMD和LMD分解與集成模型XGBoost結(jié)合后,R2分別達(dá)到0.923和0.934,與XGBoost直接預(yù)測(cè)相比分別提升0.042和0.053,但仍低于Stacking的0.969．因此,相較于其他傳統(tǒng)機(jī)器學(xué)習(xí)、深度學(xué)習(xí)方法和集成學(xué)習(xí)模型XGBoost,Stacking模型在太陽(yáng)輻照度的短期預(yù)測(cè)上有著更高的精度,擬合能力更強(qiáng)．

為了顯示本文模型的優(yōu)越性和各改進(jìn)點(diǎn)的有效性,搭建了以下4種Stacking對(duì)比模型:

1)模型1:經(jīng)典Stacking模型(Stacking)．

2)模型2:對(duì)傳統(tǒng)Stacking模型進(jìn)行GBDT特征篩選的模型(GBDT-Stacking)．

3)模型3:對(duì)傳統(tǒng)Stacking模型預(yù)測(cè)結(jié)果使用RF算法進(jìn)行誤差修正(Stacking-RF)．

4)模型4:對(duì)傳統(tǒng)Stacking模型進(jìn)行權(quán)重分配與Box-Cox處理的模型(賦權(quán)Stacking)．

由此設(shè)計(jì)了消融實(shí)驗(yàn)來(lái)分析各個(gè)改進(jìn)點(diǎn)對(duì)Stacking模型預(yù)測(cè)性能的影響,并將各模型的預(yù)測(cè)結(jié)果與輻照度實(shí)際值進(jìn)行橫向?qū)Ρ?結(jié)果如圖6所示,各消融實(shí)驗(yàn)?zāi)Ｐ偷慕^對(duì)誤差如圖7所示,消融實(shí)驗(yàn)?zāi)Ｐ偷脑u(píng)價(jià)指標(biāo)值如表3所示．

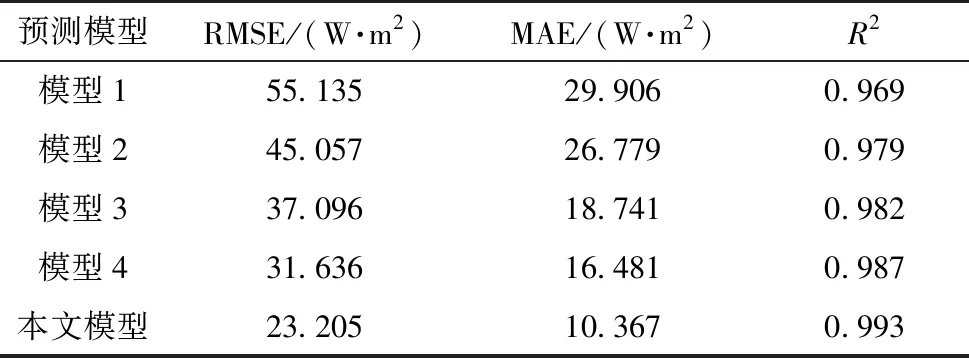
表3 不同模型的評(píng)價(jià)指標(biāo)

圖6 對(duì)比模型與本文所提模型的預(yù)測(cè)結(jié)果Fig.6 Prediction result comparison between the proposed method and classic or modified Stacking models

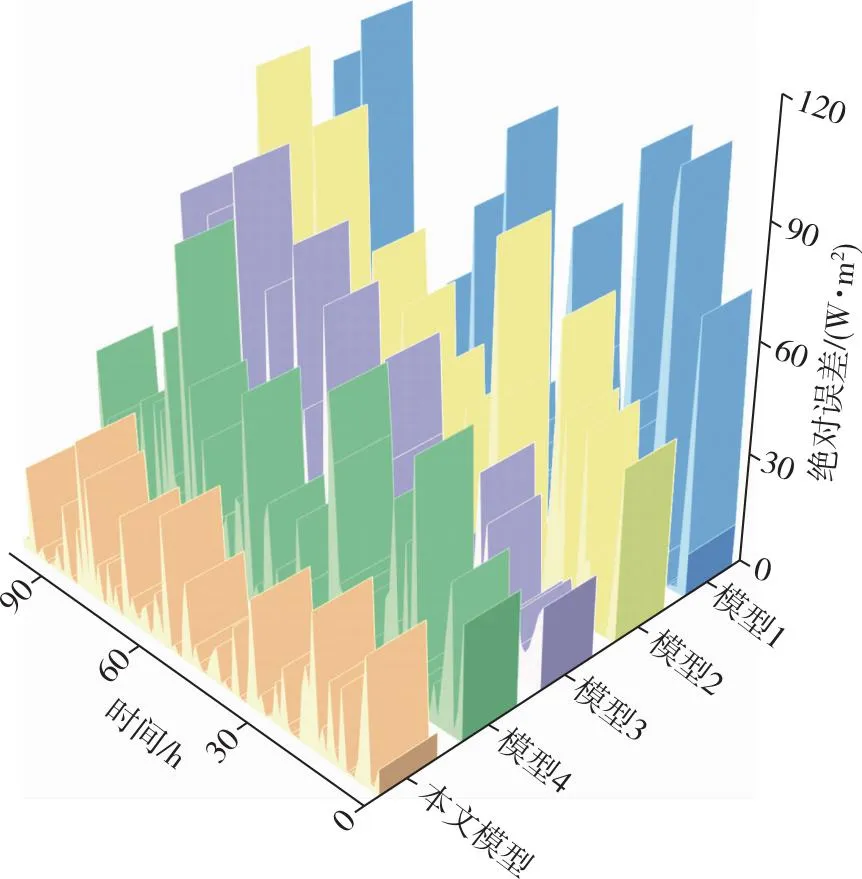
圖7 對(duì)比模型與本文所提模型預(yù)測(cè)誤差Fig.7 Prediction error comparison between the proposed method and classic or modified Stacking models

由表3可知:本文模型相較于Stacking、GBDT-Stacking、Stacking-RF及賦權(quán)Stacking模型,R2分別提升0.024、0.014、0.011和0.006,MAE分別降低65.3%、61.3%、44.7%和37.1%．另外還可以看出:模型4相較于擁有相同學(xué)習(xí)器的模型1預(yù)測(cè)效果提升明顯且誤差波動(dòng)較小;模型2和模型3也可顯著提升Stacking集成模型的預(yù)測(cè)精度,其MAE分別降低10.4%和37.3%．因此,本文模型能準(zhǔn)確預(yù)估不同時(shí)期的輻照度變化趨勢(shì),預(yù)測(cè)準(zhǔn)確度較Stacking模型有較大提升．

4 結(jié)語(yǔ)

本文將基于Box-Cox變換和權(quán)值分配的改進(jìn)Stacking模型應(yīng)用于短期輻照度預(yù)測(cè)領(lǐng)域,使用4種相互異質(zhì)的算法作為學(xué)習(xí)器,充分利用各算法在數(shù)據(jù)特征結(jié)構(gòu)與特征空間上的不同視角,從而使Stacking集成模型的優(yōu)越性得以充分發(fā)揮．同時(shí),采用GBDT算法進(jìn)行特征選取和RF算法對(duì)誤差進(jìn)行修正,達(dá)到了簡(jiǎn)化計(jì)算復(fù)雜度和提升輻照度預(yù)測(cè)精度的目的．實(shí)驗(yàn)結(jié)果表明:

1)通過(guò)對(duì)數(shù)據(jù)進(jìn)行特征重要度分析,篩選掉相關(guān)度較弱的特征,達(dá)到了過(guò)濾冗余特征,構(gòu)造出效率精度更高、復(fù)雜度更低的獨(dú)立預(yù)測(cè)模型的目的．

2)引入誤差修正算法計(jì)算擬合Stacking集成模型預(yù)測(cè)結(jié)果的動(dòng)態(tài)誤差,獲得余項(xiàng)預(yù)測(cè)值,通過(guò)加法模型融合預(yù)測(cè)值與余項(xiàng)得到最終輻照度預(yù)測(cè)值．結(jié)果表明,通過(guò)將余項(xiàng)融合進(jìn)預(yù)測(cè)結(jié)果能降低預(yù)測(cè)誤差．

3)通過(guò)與單一預(yù)測(cè)模型以及傳統(tǒng)Stacking模型相比,表明本文所提出的改進(jìn)Stacking模型具有良好的穩(wěn)定性和較高的預(yù)測(cè)精度．