黃土地震古/老滑坡原始地形恢復方法研究

吳良杰 薄景山 彭達

摘要：

黃土地震古/老滑坡原始地形恢復是開展黃土地震古/老滑坡研究的基礎。以寧夏回族自治區固原市西吉縣平峰鄉三合村潘溝組1號滑坡為例，利用衛星遙感解譯和野外調查等技術和方法采集滑坡現今地形資料數據;并基于滑坡滑動前后滑坡體體積相等的原則，以MATLAB軟件為平臺，利用三維曲面插值技術恢復滑坡的原始地形，恢復后的滑坡原始地形斜坡坡面形態整體呈外凸型，坡度分布范圍在12°～15°間；最后，利用黃土地貌單元的坡度分布范圍和滑坡穩定性計算論證恢復結果的合理性和可行性。文章研究成果可為缺乏滑動前地形資料的黃土地震古/老滑坡原始地形的恢復提供新方法，對黃土地震古/老滑坡的研究具有重要的理論意義和工程應用價值。

關鍵詞：

黃土古老滑坡; 地形恢復; 三維曲面插值; 地形數據; 穩定性計算

中圖分類號： P694;P642????? 文獻標志碼：A?? 文章編號： 1000-0844（2023）02-0329-09

DOI：10.20000/j.1000-0844.20211006002

Restoration method of the original topography of

ancient seismic landslides in loess areas

WU Liangjie1， BO Jingshan2，3， PENG Da3

（1. Geophysical Exploration Center， CEA， Zhengzhou? 450011， Henan， China;

2. Key Laboratory of Earthquake Engineering and Engineering Vibration， Institute of Engineering Mechanics，

CEA，Harbin 150080， Heilongjiang， China;

3. Institute of Disaster Prevention， Sanhe 065201， Hebei， China）

Abstract：

Restoration of the original topography is the basis for the study of ancient seismic landslides in loess areas. The No.1 landslide in the Pangou Group， Sanhe Village， Pingfeng Township （Xiji County， Ningxia Hui Autonomous Region） was taken as an example in this paper. Satellite remote sensing interpretation and field survey were adopted to collect the current topographic data of the landslide. Based on the principle of equal volumes of landslide bodies before and after sliding， MATLAB was used to restore the original topography of the No. 1 landslide using 3D surface interpolation technology. The surface shape of the restored landslide's original topography is generally convex， with a slope distribution range of 12°—15°. Finally， the rationality and feasibility of the restoration results were demonstrated by the slope distribution range of the loess geomorphic units and the landslide stability calculation. Results provide a novel approach for the restoration of the original topography of ancient seismic loess landslides that lacks the topography data before sliding， thus providing important theoretical significance and engineering application value for related studies.

Keywords：

ancient loess landslide; topography restoration; 3D surface interpolation; topography data; stability calculation

0 引言

黃土地震滑坡是黃土地區典型的地震地質災害［1］。地震災害資料顯示，黃土地區歷次中強地震都誘發了大量的黃土滑坡，如1654年天水8.0級特大地震誘發了180多個規模不等的黃土地震滑坡，滑坡分布總面積達1 000 km2［2-3］;1718年通渭7.5級大地震共誘發了300多起大規模的黃土地震滑坡，分布總面積達3 500 km2［4］;1920年海原8.5級特大地震約誘發了600多起大規模的黃土地震滑坡，分布面積達4 000～5 000 km2［5-7］。因此，開展黃土地震滑坡研究對減輕黃土地區的地震災害具有重要的理論意義和工程應用價值。本文所稱古/老滑坡是工程地質學中古滑坡和老滑坡的統稱［8］。由于形成在黃土地區的古/老滑坡數量多，種類齊全，且形態保留較完整，因此可通過黃土古/老滑坡的研究來探索黃土地震滑坡的形成機理和形成條件。開展黃土地震滑坡研究需要掌握滑坡滑動前的地形資料，但是黃土古/老滑坡由于形成年代久遠，無法獲取相關地形資料，因此開展黃土地震古/老滑坡原始地形恢復方法的研究已成為當前滑坡研究領域一個亟待解決的問題。古/老滑坡地形恢復研究工作始于21世紀初，李忠生［9］、李萍［10］、Conoscenti C等［11］、鄭旭輝［12］、周鑫等［13］針對不同的研究問題提出了一些古/老滑坡地形恢復方法，取得了一定的研究成果，但現有的古/老滑坡原始地形恢復方法精度不高，遠不能滿足實際工作的需要。

本文基于滑坡體滑動前后體積相等的原則，結合MATLAB中三維曲面插值程序Gridfit［14］和三次樣條插值程序Spline［15］，提出一種黃土地震古/老滑坡原始地形的恢復方法。該方法的思路為：在采集滑坡現今地形數據的基礎上，估算黃土地震滑坡體的體積，并以剪出口最低點與滑坡后緣最高點連線的傾角作為滑坡滑動前斜坡的原始坡度，通過三維曲面插值技術對滑坡周界的地形數據和滑坡剪出口與滑坡后緣連線上的點進行插值和擬合，從而近似得到滑坡滑動前斜坡的地表形狀；在此基礎上，利用滑坡的地形數據建立一個滑坡滑動前的初始斜坡地形模型，在此模型的基礎上估算出滑坡體滑動前的體積；最后，基于滑坡體滑動前與滑動后體積相等的原則，通過調整模型坡面的凹凸程度得到滑坡滑動前的最終地形模型。并利用該方法對寧夏固原市西吉縣平峰鄉三合村潘溝組1號滑坡開展原始地形恢復工作，論證恢復結果的合理性。

1 滑坡概況

三合村1號滑坡位于寧夏回族自治區固原市西吉縣平峰鄉三合村潘溝組，系1920年海原8.5級特大地震引發的滑坡。其位于地震烈度IX度區內，地理坐標為105.49° E，35.79° N。由于西北黃土地區氣候干旱，降雨量少，滑坡的地貌形態保留較完整。滑坡現今地貌和等高線分別如圖1和圖2所示。我們通過野外調查和衛星遙感解譯，獲得該滑坡的基本信息：滑坡主滑動方向約為70°方向，主滑長度約832 m，寬度約298 m，原始坡高為 154 m;周邊未滑動區域的坡角為 16.3°，滑坡體坡角為 6°;滑坡后壁高差為58 m，后壁傾角為39°;滑坡左側壁高差為24.5 m，左側壁傾角為46.5°;滑坡右側壁高差為20 m，右側壁傾角為40°。通過現場估算，滑坡體最大滑距約為360 m。該滑坡在平面上大致呈矩形，地層結構為泥巖-黃土二元結構：下部為白堊紀的紅色泥巖，隔水性能較好，遇水強度降低;其上為第四紀馬蘭黃土，厚度約為60 m。在滑坡滑動面上未見明顯的紅色泥巖出露，因此可判定其為黃土層內滑坡。綜合衛星遙感解譯和現場調查的結果，判定該滑坡形成于黃土梁地貌，其地質剖面圖如圖3所示。

2 滑坡邊界確定和地形數據采集

2.1 滑坡周界、剪出口和原始周界的確定

滑坡周界是滑坡體與周邊未滑區域的分界線，它圈定了滑坡在平面上的范圍［16］。在衛星影像中，通常取滑坡滑動區域與周邊未滑區域之間地表輪廓不連續或銜接不和諧的分界線作為滑坡周界，如圖4所示。滑坡剪出口是滑動面最下端與原地面相交剪出的破裂帶，或滑動面最下端與原始地面的交線［17］，通常作為滑坡滑動前原始周界最下端的界限，但剪出口通常被掩埋于滑坡體之下，不易獲取。工程上獲取剪出口信息的方法有鉆探、物探等，但這些方法成本高、費時費力，對研究區域性滑坡不具備普適性。根據野外調查的經驗，滑坡剪出口的位置通常位于滑坡側壁最下端附近，因此，為了方便和快速地確定滑坡剪出口的位置，本研究根據野外調查的結果，取滑坡兩側壁邊界線最下端位置的連線作為滑坡剪出口的大致位置，并取剪出口的中點位置為其最低點，將滑坡前緣最低點的高程值作為剪出口最低點的高程值。同時，取滑坡后緣、滑坡側壁頂部邊界線和滑坡剪出口三者所圍成的閉合線作為滑坡滑動前的原始周界，如圖5所示。

2.2 滑坡地形資料的采集

基于30 m精度的DEM高程數據，可根據不同地形要素的特點，按照不同的采樣間隔來采集滑坡不同要素的地形數據。利用91衛圖助手軟件分別采集三合村1號滑坡的滑坡后壁、滑坡后緣、滑坡體、滑坡側壁頂部邊界、滑坡舌、滑坡剪出口和未滑區域不動體等部位的地形數據，采樣點位置分布如圖6所示。本文采集地形數據坐標時，采用國際通用的地理投影坐標系——WGS84高斯投影坐標系，地形數據單位統一采用m。

3 滑動面確定和滑體體積的估算

滑動面位置和滑坡體體積是滑坡原始地形恢復中兩個重要的幾何參數。在已采集的滑坡地形資料的基礎上，利用MATLAB軟件中的三次樣條插值程序進行插值，可近似得到滑動面的位置。在此基礎上，結合滑動面與滑坡體表面之間的高差和滑坡體的表面積，近似估算出滑坡體的體積。

3.1 滑動面的確定

結合野外調查經驗，提出一種利用三次樣條函數插值確定滑動面的快捷方法。由于三次樣條函數插值在三維坐標系中有一定的局限性，但在二維坐標系中則比較成熟，因此在插值前需將三維坐標系中的插值轉化為二維坐標系的插值。在三維坐標系的基礎上，以滑坡后緣最高點的水平投影點為原點O′，豎向高程為Z軸，滑坡后緣最高點與剪出口最低點的連線的水平向投影方向為S軸，建立一個S-Z二維坐標系進行插值。具體步驟如下：

第一步，將滑坡后壁、滑坡體、剪出口最低點等位置的采樣點換算至S-Z坐標系中;

第二步，確定一個調整系數，確定方法為取滑坡后壁高差、滑坡左側壁高差以及右側壁高差二分之一的平均值作為該系數值，取滑坡體中點位置采樣點的高程值減去調整系數所得到的點作為滑動面的中點位置;

第三步，以滑坡后壁、滑動面中點位置和剪出口最低點位置的采樣點為被插值點，利用三次樣條插值程序對其進行插值來近似確定滑動面的位置，如圖7所示；

第四步，將已得到的滑動面位置的插值點和滑坡地形數據換算至三維坐標系中，利用MATLAB軟件的三維曲面插值程序Gridfit對滑動面位置的插值點和滑坡其他地形采樣點進行插值，得到滑動面的近似三維地形數據;

第五步，利用MATLAB中的meshz程序對滑動面的三維地形數據進行擬合，得到滑動面的三維地形圖（圖8）。

該方法目前僅適用于一般性的黃土層內滑坡，不適用于其他非黃土層內的滑坡。

3.2 滑坡滑動后體積的估算

利用滑坡體表面積與滑坡體平均厚度的乘積來估算滑坡體的體積：

Va=Sa×Ha （1）

式中：Sa為滑動后滑坡體的表面積，近似取自滑坡體表面積的水平投影面積，利用91衛圖助手軟件的面積測量功能測得三合村1號滑坡的Sa值約為246 854.2 m2（圖9）;Ha為滑動后滑坡體的平均厚度，取滑坡體現今地表與滑動面以及滑坡舌以下原地面之間若干點高差的平均值（圖10），通過計算得到三合村1號滑坡的Ha值約為13 m;Va為滑動后滑坡體的體積，估算得出三合村1號滑坡的Va值約為3 209 105.0 m3。

4 滑坡原始地形的恢復

野外調查和有關研究工作表明，自然形成的黃土斜坡坡面形態大致分為平直型、內凹型、外凸型三種［18］。因此，在滑坡原始地形恢復中，可首先假定滑坡滑動前的斜坡坡面形態為平直型，再利用MATLAB的三維曲面插值程序Gridfit和三次樣條插值程序Spline對所采集的滑坡地形數據進行插值和擬合，近似得到其初始的三維地表形態。在此基礎上，基于滑坡體滑動前后體積相等的原則，對斜坡的坡面形態進行適當調整，以此來確定滑坡滑動前的三維地形。

4.1 滑動前斜坡初始地形模型的建立

假定滑坡滑動前斜坡的坡面形態為平直型，在S-Z坐標系中繪制滑坡滑動前的斜坡剖面圖（圖11）。取滑坡后緣最高點與剪出口最低點的連線為滑動前斜坡的坡面，取該線的傾角為滑動前斜坡的坡度α，通過計算得到三合村1號滑坡的α為14°。通過擬合得到該直線在Z-S坐標中的數學表達式：

Z=-0.246 4S+1 963 （2）

利用式（2），采用等間隔的方式求得滑動前斜坡坡面上若干點的高程值，將這些點換算至三維坐標系中。在三維坐標系中，利用MATLAB軟件中的三維曲面插值程序Gridfit對斜坡坡面上的若干點和滑坡其余地形采樣點進行插值，再利用meshz程序對所得到的插值點數據進行擬合，得到三合村1號滑坡滑動前斜坡的三維地形圖（圖12）。

4.2 滑坡滑動前滑體體積的估算

采用滑坡體表面積與平均厚度的乘積來估算滑動前滑坡體的體積Vb值：

Vb=Sb×Hb （3）

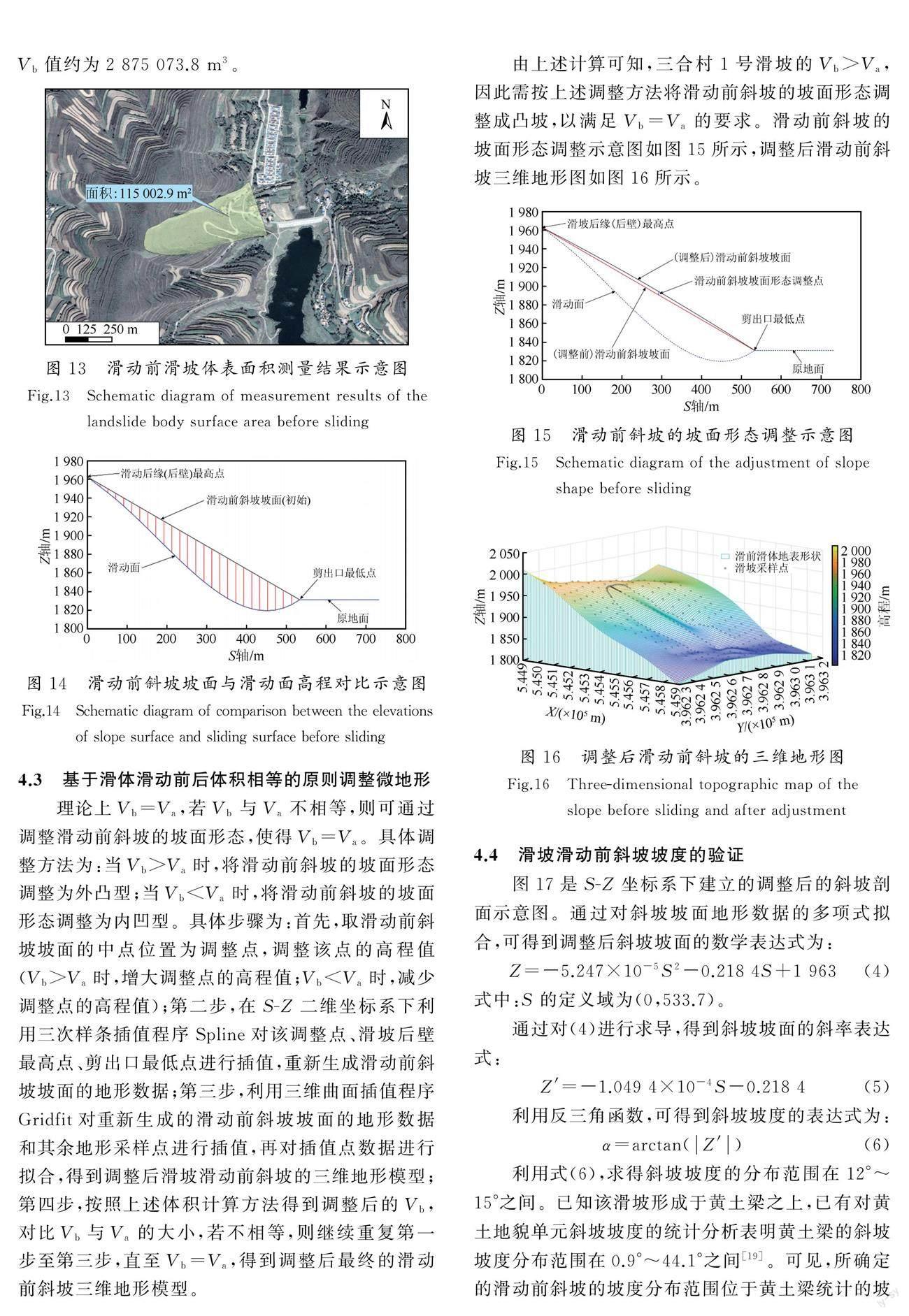
式中：Sb為滑動前滑坡體的表面積，主要根據滑坡原始周界所圈定的區域范圍內滑坡體表面積的水平投影面積確定，圖13給出三合村1號滑坡Sb的測量結果約為115 002.9 m2;Hb為滑動前滑坡體的平均厚度，取自滑動前斜坡坡面與滑動面之間若干點的高差的平均值，通過計算得到三合村1號滑坡的Hb值約為25 m。滑坡滑動前斜坡坡面與滑動面高程對比如圖14所示。經過估算，三合村1號滑坡的Vb值約為2 875 073.8 m3。

4.3 基于滑體滑動前后體積相等的原則調整微地形

理論上Vb=Va，若Vb與Va不相等，則可通過調整滑動前斜坡的坡面形態，使得Vb=Va。具體調整方法為：當Vb>Va時，將滑動前斜坡的坡面形態調整為外凸型;當VbVa時，增大調整點的高程值;Vb

由上述計算可知，三合村1號滑坡的Vb>Va，因此需按上述調整方法將滑動前斜坡的坡面形態調整成凸坡，以滿足Vb=Va的要求。滑動前斜坡的坡面形態調整示意圖如圖15所示，調整后滑動前斜坡三維地形圖如圖16所示。

4.4 滑坡滑動前斜坡坡度的驗證

圖17是S-Z坐標系下建立的調整后的斜坡剖面示意圖。通過對斜坡坡面地形數據的多項式擬合，可得到調整后斜坡坡面的數學表達式為：

Z=-5.247×10-5S2-0.218 4S+1 963 （4）

式中：S的定義域為（0，533.7）。

通過對（4）進行求導，得到斜坡坡面的斜率表達式：

Z′=-1.049 4×10-4S-0.218 4 （5）

利用反三角函數，可得到斜坡坡度的表達式為：

α=arctan（Z′） （6）

利用式（6），求得斜坡坡度的分布范圍在12°～15°之間。已知該滑坡形成于黃土梁之上，已有對黃土地貌單元斜坡坡度的統計分析表明黃土梁的斜坡坡度分布范圍在0.9°～44.1°之間［19］。可見，所確定的滑動前斜坡的坡度分布范圍位于黃土梁統計的坡度范圍內，因此本文給出的三合村1號滑坡滑動前的斜坡坡角在合理區間內。

5 三合村1號滑坡穩定性驗算

基于恢復后的三合村1號滑坡地形，利用AutoCAD、Geostudio軟件建立相應的斜坡計算模型，并采用擬靜力法對滑動前斜坡的計算模型進行穩定性分析。

5.1 計算模型的建立

根據三合村1號滑坡滑動前的斜坡剖面圖和滑坡外擴一定范圍內的采樣點數據，利用AutoCAD、Geostudio軟件建立如圖18所示的滑坡計算模型。該滑坡屬于黃土層內滑坡，因此計算模型的地層結構可概化為均質黃土結構，黃土為第四系馬蘭黃土，斜坡的坡面形狀為外凸形。模型的水平向長度約為900 m，豎直向高度約為200 m，單元網格的尺寸設置為3 m，共劃分了15 558節點，15 284個單元。依據黃土樣品的室內實驗結果，并參考黃土參數的經驗數據，將黃土層的物理力學參數列于表1。

5.2 斜坡初始應力分析

將上述計算模型和土層的物理力學參數導入Geostudio軟件，利用該軟件的SIGMA/W模塊快速完成斜坡的初始應力分析計算（自重作用下的應力分布），計算結果如圖19、20所示，其中σY代表豎直向的土壓應力，σX代表水平向土的側向壓應力。該結果可作為三合村1號滑坡穩定性分析的初始條件。

5.3 利用擬靜力法計算穩定性系數

擬靜力法是將地震作用等效為作用于滑坡體質心的對斜坡穩定最不利的慣性力，根據極限平衡理論可計算出沿指定滑動面的穩定性系數［20-21］。該方法極大地簡化了地震動對斜坡體的作用過程，由于計算過程比較簡單，因此被廣泛應用于巖土工程設計領域。對于作用在每個土條質心位置的水平向地震荷載，可按《水利水電工程邊坡設計規范》［22］推薦的公式進行計算：

Fhi=αhξWiαi/g （7）

式中：Fhi為作用在第i條土條上的水平向地震荷載;ξ為地震作用的動態分布系數;αi為地震作用的折減系數;Wi為第i個土條的重量;αh為地震動峰值加速度。經換算，施加在每個土條質心位置的水平向地震加速度α為：

α=αhξαi （8）

按照規范要求，ξ，αi分別取值為1.0和0.25。已知三合村1號滑坡地處1920年海原8.5級特大地震IX度區，可取其水平地震動峰值加速度為0.4g。利用Geostudio軟件的SLOPE/W模塊，分別采用瑞典條分法［23］、畢肖普條分法［24］和簡布條分法［25］計算了三合村1號滑坡的穩定性系數，計算結果列于表2。

由表2可知，三合村1號滑坡在0.4g的水平向地震動峰值加速度作用下，采用不同方法計算的穩定性系數均小于1，說明在該地震動作用下會發生失穩破壞。這與實際情況吻合，在一定程度上說明了本文地震古/老滑坡原始地形恢復方法的合理性。

6 結論

黃土地震古/老滑坡原始地形恢復是開展地震古/老滑坡研究的一項基礎性和必不可少的工作，開展這項工作的難度較大。本文在已有研究工作的基礎上［26］，利用滑坡地形資料，基于滑坡體滑動前后體積相等的原則，以MATLAB軟件為操作平臺，初步提出了一種黃土地震古/老滑坡原始地形恢復方法，并利用該方法恢復了寧夏回族自治區西吉縣平峰鄉三合村1號滑坡的原始地形，驗證了地形恢復結果的合理性和可行性。

本文提出的恢復方法具有方便、快捷的優點，且考慮到了較多的因素，恢復精度較以往的方法有所提高，適用于區域性地震黃土滑坡研究，對黃土古/老滑坡的研究有一定的理論意義和工程應用價值。但該方法在滑動面位置、滑坡體體積、斜坡坡面具體凹凸形態的確定等方面還有待深入開展研究工作，在精度上仍需進一步提高。

參考文獻（References）

［1］ 王蘭民.黃土動力學［M］.北京：地震出版社，2003：144-150.

WANG Lanmin.Loess dynamics［M］.Beijing：Seismological Press，2003：144-150.

［2］ 袁道陽，雷中生，王愛國.1654年甘肅天水南8級地震補充考證［J］.地震工程學報，2017，39（3）：509-520.

YUAN Daoyang，LEI Zhongsheng，WANG Aiguo.Additional textual criticism of southern Tianshui M8 earthquake in Gansu Province in 1654［J］.China Earthquake Engineering Journal，2017，39（3）：509-520.

［3］ 趙云.1654年甘肅天水地震烈度和震級考析［J］.高原地震，2008，20（2）：30-33，29.

ZHAO Yun.Textual research on the intensity and magnitude of Gansu Tianshui earthquake in 1654［J］.Plateau Earthquake Research，2008，20（2）：30-33，29.

［4］ 彭達，楊順，李孝波.甘肅通渭縣黃土地震滑坡分布特征及發育機理［J］.中國地質災害與防治學報，2017，28（3）：31-38.

PENG Da，YANG Shun，LI Xiaobo.Distribution and mechanism of loess landslides induced by earthquake in Tongwei，Gansu Province［J］.The Chinese Journal of Geological Hazard and Control，2017，28（3）：31-38.

［5］ 郭增建，謝原定，李孟鑾，等.1920年12月16日的海原大地震［J］.地球物理學報，1976，19（1）：42-49.

GUO Zengjian，XIE Yuanding，LI Mengluan.Great Haiyuan （海原） earthquake on December 16，1920［J］.Chinese Journal of Sinica，1976，19（1）：42-49.

［6］ 鄧龍勝，范文.寧夏海原8.5級地震誘發黃土滑坡的變形破壞特征及發育機理［J］.災害學，2013，28（3）：30-37.

DENG Longsheng，FAN Wen.Deformation breakage characteristics and development mechanism of loess landslide triggered by Haiyuan M8.5 earthquake in Ningxia［J］.Journal of Cata-strophology，2013，28（3）：30-37.

［7］ ZHUANG J，PENG J，XU C，et al.Distribution and characteristics of loess landslides triggered by the 1920 Haiyuan earthquake，Northwest of China［J］.Geomorphology，2018，314：1-12.

［8］ 《工程地質手冊》編委會.工程地質手冊［M］.5版.北京：中國建筑工業出版社，2018：651-657.

Editorial Committee of Geological Engineering Handbook.Geological engineering handbook［M］.5th ed.Beijing：China Architecture & Building Press，2018：651-657.

［9］ 李忠生.黃土滑坡的滑前地貌重建［J］.自然災害學報，2004，13（2）：96-100.

LI Zhongsheng.Pre-failure topography reconstruction for loess landslide［J］.Journal of Natural Disasters，2004，13（2）：96-100.

［10］ 李萍.黃土邊坡可靠性研究［D］.西安：長安大學，2006.

LI Ping.Reliability applied to stability analysis of loess slope［D］.Xi'an：Chang'an University，2006.

［11］ CONOSCENTI C，CIACCIO M，ALMARU CARABALLO-ARIAS N，et al.Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines：a case of the Belice River Basin （western Sicily，Italy）［J］.Geomorphology，2015，242：49-64.

［12］ 鄭旭輝.邊坡地震動力失穩概率分析方法研究：以寧夏西吉震湖斜坡為例［D］.北京：中國地質大學（北京），2018.

ZHENG Xuhui.Study on probability analysis method of slope seismic dynamic instability：a case study of Xiji Zhenhu slope in Ningxia［D］.Beijing：China University of Geosciences，2018.

［13］ 周鑫，周慶，高帥坡，等.重慶小南海滑坡原始地形恢復及滑坡體體積計算［J］.地震地質，2020，42（4）：936-954.

ZHOU Xin，ZHOU Qing，GAO Shuaipo，et al.Restoration of the original topography of the Xiaonanhai landslide in Chongqing and calculation of its volume［J］.Seismology and Geology，2020，42（4）：936-954.

［14］ 王廣，邢林芳.MATLAB GUI程序設計［M］.北京：清華大學出版社，2018：115-128.

WANG Guang，XING Linfang.MATLAB GUI programming［M］.Beijing：Tsinghua University Press，2018：115-128.

［15］ 邢麗.三次樣條插值端點約束條件的構造與Matlab實現［J］.上海第二工業大學學報，2012，29（4）：319-323.

XING Li.Structure and Matlab implementation of cubic spline interpolation endpoint constraints［J］.Journal of Shanghai Second Polytechnic University，2012，29（4）：319-323.

［16］ 鄭穎人，陳祖煜，王恭先.邊坡與滑坡工程治理［M］.2版.北京：人民交通出版社，2010：16-20.

ZHENG Yingren，CHEN Zuyu，WANG Gongxian.Engineering treatment of slope & landslide［M］.2nd ed.Beijing：China Communications Press，2010：16-20.

［17］ 成永剛.滑坡區域性分布規律與防治［M］.北京：人民交通出版社，2014：24-28.

CHENG Yonggang.Regional distribution rules and prevention of landslides［M］.Beijing：China Communications Press，2014：24-28.

［18］ 王振宇，張常亮，周瀟朗，等.土質滑坡滑前三維地形恢復研究［J］.甘肅科學學報，2020，32（1）：72-78.

WANG Zhenyu，ZHANG Changliang，ZHOU Xiaolang，et al.Study on the restoration of three-dimensional terrain before the landslide［J］.Journal of Gansu Sciences，2020，32（1）：72-78.

［19］ 吳良杰，薄景山，牛潔.黃土地區地形特征參數分布特征的統計分析［J］.科學技術與工程，2021，21（21）：8797-8806.

WU Liangjie，BO Jingshan，NIU Jie.Statistical analysis on the distribution characteristics of topographical parameters in loess area［J］.Science Technology and Engineering，2021，21（21）：8797-8806.

［20］ 薄景山，段玉石，常晁瑜，等.斜坡地震穩定性研究的若干問題［J］.自然災害學報，2019，28（1）：1-8.

BO Jingshan，DUAN Yushi，CHANG Chaoyu，et al.Some problems of study on slope stability under earthquake［J］.Journal of Natural Disasters，2019，28（1）：1-8.

［21］ 唐世雄，鄧廣輝，劉衡秋.斜坡抗震穩定性分析中擬靜力法的應用研究［J］.城市地質，2020，15（2）：181-186.

TANG Shixiong，DENG Guanghui，LIU Hengqiu.Study on the application of pseudo-static method in the analysis of seismic stability of slope［J］.Urban Geology，2020，15（2）：181-186.

［22］ 中華人民共和國水利部.水利水電工程邊坡設計規范：SL 386—2007［S］.Beijing：China Water & Power Press.

Ministry of Water Resources of the People's Republic of China.Design code for engineered slopes in water resources and hydropower projects：SL 386—2007［S］.Beijing：China Water & Power Press.

［23］ 東南大學，浙江大學，湖南大學.土力學［M］.4版.北京：中國建筑工業出版社，2016.

Southeast University，Zhejiang University，Hunan University.Soil mechanics［M］.4th ed.Beijing：China Architecture & Building Press，2016.

［24］ BISHOP A W.The use of the slip circle in the stability analysis of slopes［J］.Géotechnique，1955，5（1）：7-17.

［25］ JANBU N，BJERRUM L，KJAERNSLI B，et al.Soil mechanics applied to some engineering problems［R］.Osio：Norwegian Geotechnical Institute Publication，1956：25-31.

［26］ 吳良杰.黃土古老滑坡原始地形恢復方法及其應用研究［D］.廊坊：防災科技學院，2021.

WU Liangjie.Research on the original terrain restoration method of loess ancient landslide and its application［D］.Langfang：Institute of Disaster Prevention，2021.