靜動載約束桁架結構拓撲優化的微分演化算法

胡長遠，傅長榮，季光耀

（1.麗水學院工學院，浙江 麗水 323000；2.浙西南地質災害研究所，浙江 麗水 323000）

結構拓撲優化是指以連續體開孔的數量及位置，或以離散體結構的節點布局、節點間的桿件連接關系為研究對象，通過改變結構的受力體系尋求最優的布局方案。拓撲尋優雖然可以最大程度優化結構，但求解空間和可行域在優化過程中都在不斷更迭，這給結構重分析帶來困難。較之尺寸優化和形狀優化，拓撲優化具有更大的設計空間、經濟效益和復雜程度，故逐步成為優化設計領域中的焦點和難點，受到更廣泛的關注［1-3］。

目前拓撲優化方法多用于靜荷載優化，而工程實際中結構常受到動荷載的作用［4］。固有頻率是結構的重要特征，共振狀態時固有頻率的影響變得異常重要。為了保證結構的安全，須把固有頻率控制在一定范圍內［5］。拓撲優化設計靜載約束有桿件應力、節點位移和歐拉屈曲等，動載約束有固有頻率，靜動荷載約束的疊加會使計算過程更為復雜、計算效率更低，而且難以收斂，無法得到較為理想的拓撲構形［6］。桁架結構拓撲優化目前主要采用基結構法，該方法以桿件截面面積為設計變量，通過逐步刪除截面面積為足夠小值的桿件來實現拓撲優化，求解簡單方便，但存在奇異最優解問題［7］。如果用很小的斷面積求解來代替零斷面求解將受到各種約束的桁架拓撲優化問題的干擾，不僅會丟失可能存在的奇異最優解，而且會增加不必要的分析。以往的解決辦法是二階段尺寸和拓撲優化方法。該方法對尺寸和拓撲變量分別進行優化，求得最優拓撲后再進行尺寸優化，求解相對簡單，拓撲構形容易實現。然而，由于尺寸和拓撲變量在數學上不是獨立的，二階段優化方法將真實搜索空間轉化為近似域，可能會剔除包含全局最優的初始搜索域，大大增加了過早收斂的風險［8］。因此發展一些更加通用有效，能同時考慮尺寸和拓撲變量的全局優化算法來解決拓撲優化問題成為一種迫切的需要。

近年來，啟發式算法逐漸被引入到工程優化領域，如遺傳算法（GA）、微粒群算法（PSO）、和聲搜索（HS）、教與學算法（TLBO）等［9］。它們不需要梯度信息，對目標函數和約束函數性態的要求較為寬松，且能兼顧靜動態約束，因而較傳統算法而言有更廣泛的應用范圍。計算中可以處理設計變量離散、可行域狹小的問題，能有效地得到高度復雜非線性問題的全局最優解，一些啟發式優化方法已被應用于拓撲優化。Tejani 等［10］利用改進的共生生物搜索算法解決在多工況下的桁架拓撲優化問題。Dehghani 等［11］在帝國競爭算法中采用新的同化策略求解考慮尺寸、形狀、拓撲變量的桁架優化問題。Dang等［12］將改進差分進化算法用于多種變量組合的桁架結構拓撲優化。Wang 等［13］用基于黃金分割系數的人工蜂鳥算法求解桁架結構的拓撲優化問題。

自Storn 和Price 于1996 年提出微分演化算法（differential evolution，DE）之后，該方法在解決復雜的優化問題上得到了很多關注［14］。微分演化算法是一種混合算法，它結合了遺傳算法的更大種群概念和進化算法的自適應變異以及采用了貪婪選擇策略。這些特征使微分演化算法相比進化算法和遺傳算法具有更好的魯棒性和更快的收斂速度。該算法已被廣泛應用于工程優化、可靠度分析、光譜分析及無線電系統感應等領域［15-18］。

在結構工程中，微分演化算法應用于桁架拓撲優化方面的研究分析還很少。筆者將DE 算法應用于考慮尺寸和拓撲變量耦合的具有多工況靜動荷載響應約束的桁架結構拓撲優化，通過對典型算例的求解并與相關文獻的結果比較來評價筆者所提方法的有效性。

1 微分演化算法（DE）

一個包括t個參數的優化問題可以用一個t維的向量來描述，該向量可以表示為：xi=（xi1，xi2，…，xit）T∈S，i=1，2，3，…，NP。其中S∈Rn為優化問題的搜索空間；DE算法利用NP作為向量每一代的個體數。類似于遺傳算法，DE算法通過變異、交叉和選擇過程實現種群的更新進化。具體過程如下［15-16］。

1.1 變異過程

變異是為了保證種群的多樣性，同時用合適的參數變化來指導已有的目標向量在合適的時間內達到一個更好的結果，從而保證了搜索的魯棒性。

1.2 交叉過程

與GA 算法相似，DE 算法中的個體經過變異后也進行交叉操作。對于群體中第G+1代經過變異過程后的向量個體按照式（2）進行交叉，將產生新的個體：

式中：j=1，2，…，t；rand（j）∈［0，1］，是t個0～1 相互獨立的隨機數中的第j個；randn（i）是隨機從集合{1，2，…，t} 中取得個體向量維度的序號；CR為交叉因子，將決定個體之間交叉的概率。

1.3 選擇過程

DE 算法采用和GA 算法不同的貪婪準則：通過比較由變異和交叉產生的子代個體和父代個體，選擇適應值好的變量，即如果父代個體適應值更優將繼續保留在種群中，否則保留子代個體。選擇過程如式（3）所示：

2 桁架結構拓撲優化

2.1 桁架結構拓撲優化的數學模型

結合拓撲優化的設計思想，構建以結構構件尺寸和拓撲變量為設計變量，以結構重量極小化為目標函數，受多工況荷載作用，考慮固有頻率、桿件應力、節點位移、歐拉屈曲以及動態失穩等約束的離散型結構拓撲優化的數學模型，表達式為：

式中：X是設計向量，A1，A2，…，Am為桿件截面積，B1，B2，…，Bm為拓撲變量；Ai、Ei、Li、ρi、σi、σcri和Bi分別是第i類設計變量的截面面積、彈性模量、桿件長度、密度、桿件應力、歐拉屈曲應力和拓撲值。設Alim為桿件的臨界面積，當Ai小于Alim時，Bi等于0，表示桿件刪除；當Ai大于等于Alim時，Bi等于1，表示桿件保留。bj和δj分別表示節點j的質量和位移；ki為歐拉屈曲系數；fr是第r階固有頻率。上標 “comp” 表示抗壓， “max” 和 “min” 分別表示上下限值。

數學模型中的約束函數還包括結構動態穩定性檢查g6和有效性檢查g7，前者是為了避免不穩定結構的出現，后者則是為了保證荷載作用點和支承節點等基本節點不被刪除。由于結構的拓撲構形是由DE算法迭代時隨機操作產生的，難免會出現一些不穩定的拓撲結構，因此有必要對新生成的結構進行穩定性檢查。結構動態穩定性檢查分兩步進行：1）檢查結構自由度是否違反格魯布里爾準則；2）檢查結構的總剛度矩陣是否為正定矩陣。

采用懲罰函數法處理上述約束，如果沒有違反約束，懲罰函數F（X）為零；否則，按照以下標準執行處罰：

其中：

式（12）中：q為違反約束的個數；pi和分別表示違反的約束值及其限值；β1和β2為系數，本文均取1.5。

2.2 基于DE算法的桁架結構拓撲優化程序

為了提高DE算法的拓撲優化效率，采用以下改進策略和技巧：1）對于離散型結構拓撲優化，取截面下限Amin=-Amax，將搜索空間轉為約兩倍的設計變量限值，這樣會豐富拓撲構形，有利于算法快速尋找到全局最優拓撲方案。2）對DE 初始隨機生成以及經迭代交叉變異后生成的拓撲構形進行動態穩定性和有效性檢查。若不滿足要求，則更新個體，不再進入有限元計算，減少計算量。3）計算過程中，一旦桿件被刪除，接續刪除其連接，重新構建有限元模型，消除應力矩陣的奇異性，避免不必要的分析。

結合DE算法及前述拓撲優化數學模型，可以給出圖1所示的離散型結構拓撲優化設計流程圖。由算法原理及優化設計流程圖可知，DE算法原理簡單，能方便地應用到結構的拓撲優化設計中。

圖1 基于DE算法的離散型結構拓撲優化設計流程圖

3 算例分析

為驗證筆者方法對桁架結構拓撲優化設計的有效性，以下對3 個典型桁架結構進行分析，通過改變桿件尺寸以及拓撲構形獲得最小重量，并與其他算法的結果進行比較。對所有問題，歐拉屈曲系數（ki，i=1，2，…，m）和節點質量（bj，j=1，2，...，n）分別取為4.0和5 kg。DE算法的參數選擇如下：F1=0.75，F=0.6，CR=0.85，20 桿和24 桿平面桁架算例種群規模NP 均取為100，72 桿空間桁架算例則取150。

3.1 24桿平面桁架

圖2 所示為24 桿平面桁架的基結構，材料的彈性模量E=6.9×1010Pa，密度ρ=2 740 kg/m3，節點3上有雙向集中質量500 kg。頻率約束為f1≥30 Hz，應力約束為±172.43 MPa，節點5、6 豎向位移約束為δmax=10 mm。設計變量為連續變量，其下限為-40 cm2，上限為40 cm2，臨界截面面積為1 cm2。兩工況下節點荷載見表1。

表1 24桿平面桿桁架荷載工況

圖2 24桿平面桁架的基結構

24桿平面桁架拓撲優化的目標函數收斂曲線見圖3，優化后桁架最優拓撲布局見圖4。為了驗證筆者方法的有效性，與文獻［8，12，19-22］相比較，對比結果見表2。

表2 24桿平面桁架拓撲優化結果比較

圖3 24桿平面桁架拓撲優化的目標函數收斂曲線

圖4 24桿平面桁架的最優拓撲形狀

由圖3可知：考慮靜動荷載多種約束時，24桿平面桁架拓撲優化在迭代約150次后已經收斂，收斂速度快，不易陷入局部最優解。在表2 中，第1階固有頻率和節點6的豎向位移均已達到限值，優化后的桁架總重量為118.895 5 kg，優于文獻［8，12，19-22］的結果。根據表2中的優化結果繪制其最優拓撲布局，如圖4 所示，最優拓撲布局與文獻［8，12，20，22］的結果相一致，桿件1～6，10～11，14，17～21，23以及節點1、4被刪除，均為穩定性結構。

3.2 20桿平面桁架

本例的基結構由9 個節點和20 根桿件組成，如圖5所示，其中節點1和9為支座，節點4上作用有荷載F1和F2。材料彈性模量E=6.9×1010Pa，密度ρ=2 740 kg/m3，兩工況下節點荷載見表3。頻率約束為f1≥60 Hz，f2≥100 Hz，應力約束為±172.43 MPa，位移約束以節點4 的豎向位移等于10 mm 和60 mm兩種情形進行計算。設計變量為連續變量，其下限為-100 cm2，上限為100 cm2，臨界截面面積為1 cm2。

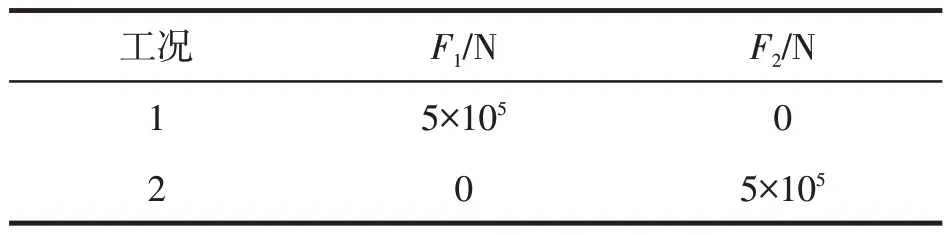
表3 20桿平面桿桁架荷載工況

圖5 20桿平面桁架的基結構

考慮不同位移約束的20桿平面桁架拓撲優化目標函數曲線見圖6，優化的最終拓撲形狀見圖7。筆者計算結果與相關文獻的比較見表4和表5。

表4 δ4y=10 mm時20桿平面桁架拓撲優化結果比較

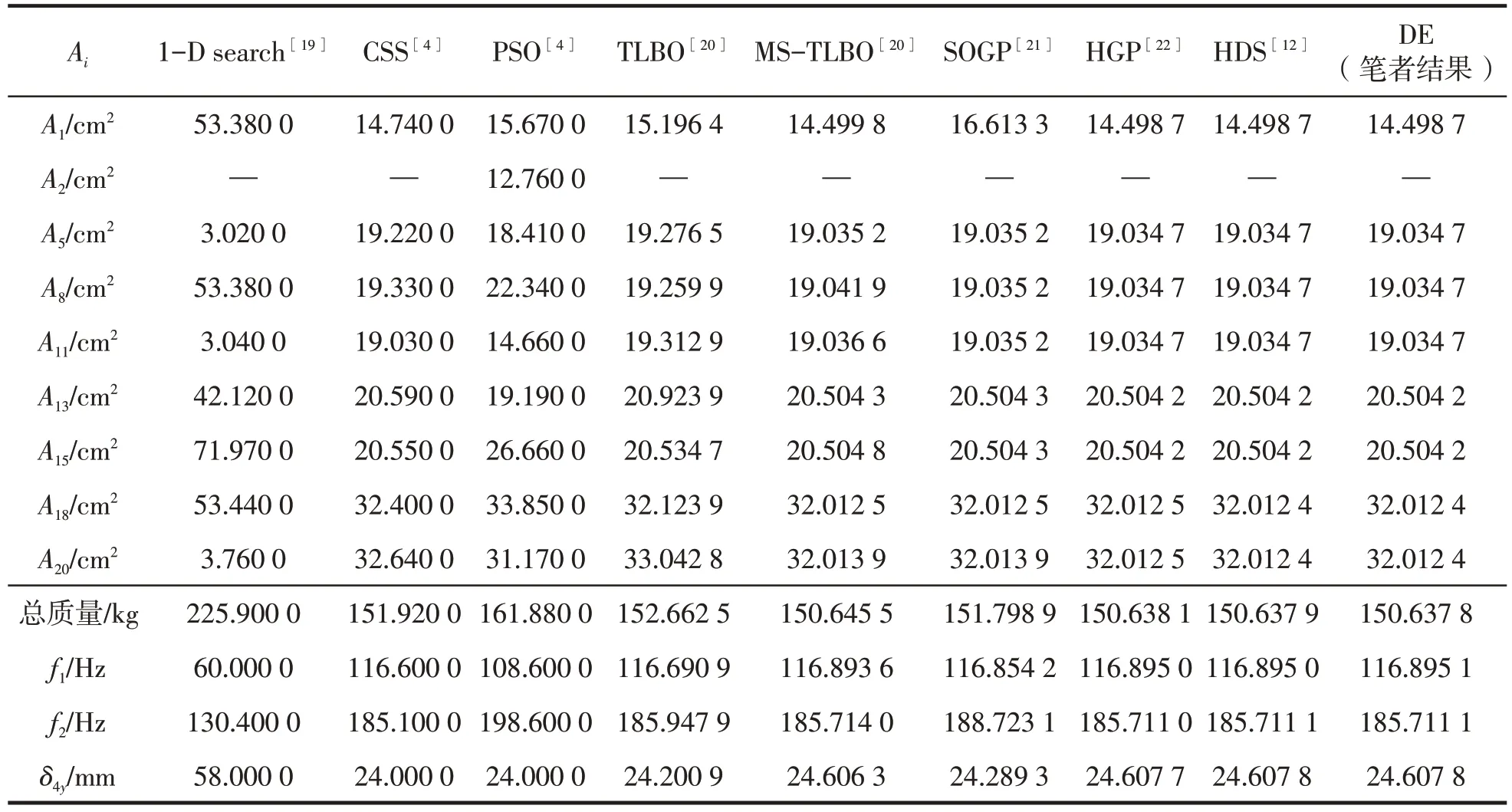
表5 δ4y=60 mm時20桿平面桁架拓撲優化結果比較

圖6 20桿平面桁架拓撲優化的目標函數收斂曲線

圖7 20桿平面桁架的最優拓撲形狀

由圖6 可知：節點4 的豎向位移約束為10 mm和60 mm時，計算分別在迭代約40次和120次后完全收斂。表4 中，節點4 的豎向位移已達到限值。由表4和表5可知，兩種情況下筆者優化后的桁架總質量分別為315.913 0 kg和150.637 8 kg，略好于文獻［12］的結果，優于文獻［4，19-22］的結果。對比表4和表5還可知，位移約束嚴苛時結構的總重量會增加。圖7所示的最優拓撲形狀中節點3、6、7被刪除，布局上具有對稱性，僅與文獻［4］不同。

3.3 72桿空間桁架

如圖8 所示的72 桿空間桁架基結構，由20 個節點和72 根桿件組成，依據結構對稱特性，桿件被分為16 組。材料彈性模量E=6.895×1010Pa，密度ρ=2 767.99 kg/m3，節點1～4 上有三向集中質量2 270 kg。頻率約束為f1≥4 Hz，f3≥6 Hz，應力約束為±172.375 MPa，節點1～4 的X和Y向位移限值為6.35 mm。設計變量為連續變量，其下限為-30 cm2，上限為30 cm2，臨界截面面積為1 cm2。兩工況下節點荷載見表6。

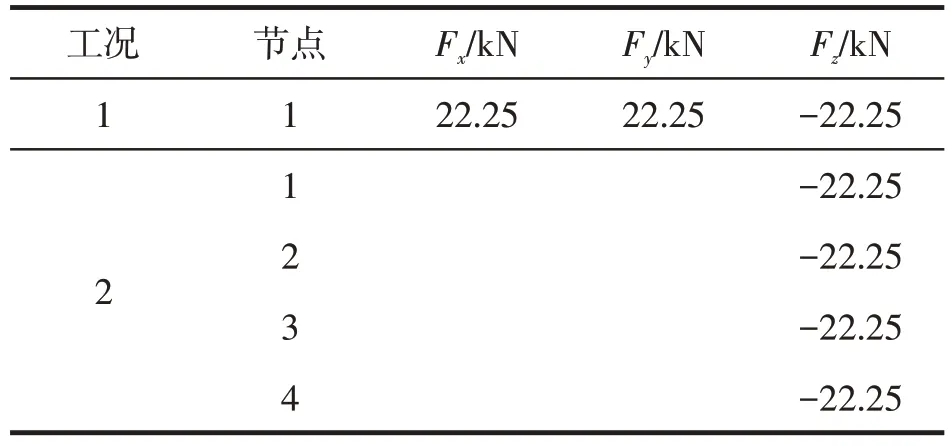
表6 72桿空間桿桁架荷載工況

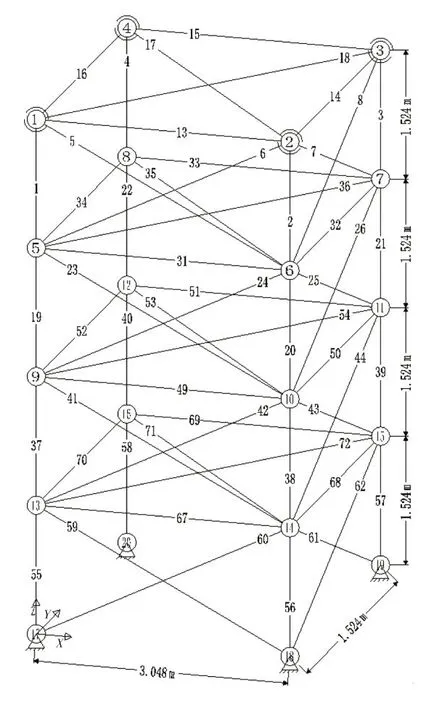
圖8 72桿空間桁架的基結構

靜動荷載約束下72桿空間桁架拓撲優化目標函數收斂曲線見圖9，與相關文獻的比較列于表7，最優拓撲形式見圖10。

表7 72桿空間桁架拓撲優化結果比較

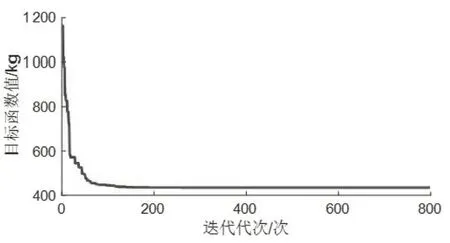
圖9 72桿空間桁架拓撲優化的目標函數收斂曲線

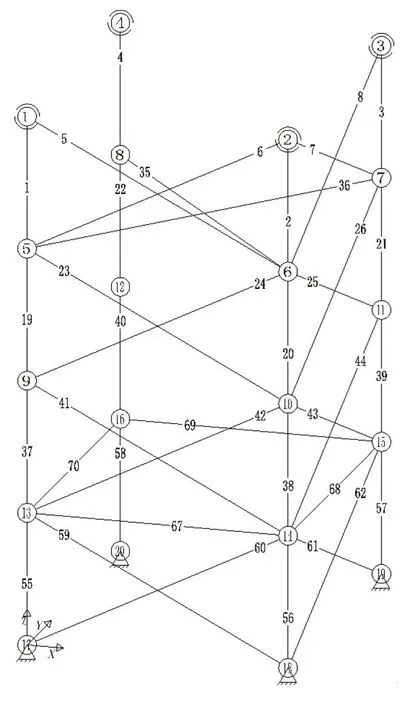
圖10 72桿空間桁架的最優拓撲形狀

圖9 結果顯示迭代約180 次時已找到最優拓撲布局方案，評價函數趨于收斂。由表7 可知：筆者DE 算法得出的桁架總質量為434.894 9 kg，優于其他所有結果，最優解受固有頻率約束控制。圖10最優拓撲形狀保留了2層外圍系桿，4層水平系桿及全部豎桿和腹桿，豎桿截面積向下逐層增大，與其他文獻結果一致。

4 結論

DE 算法是一種啟發式搜索的混合進化算法，和其他進化算法相比，DE算法不易陷入局部最優解，具有原理簡單、易于實現以及魯棒性強等優點。以往用二階段優化方法求解桁架拓撲優化，雖然降低了求解難度與計算量，但割裂了解空間而難以保證得到全局最優解。筆者在DE 算法基礎上，通過對每個桿件引入拓撲變量，便于實現同時考慮兩種不同性質設計變量的拓撲優化問題。考慮到桁架結構在實際使用時可能會因動載作用產生噪聲過大、共振等現象，需要在約束條件中引入固有頻率約束。雖然考慮靜動載約束耦合會造成求解難度的增加，但是更符合實際情況。此外，在優化過程中對有限元模型進行修正，重新構建剛度、質量和荷載矩陣，解決了矩陣奇異和不必要分析給計算帶來的困難。數值分析結果表明：筆者方法很好地保持了所得最優解的穩定性、有效性以及較強的收斂性，可以成功地進行桁架結構的拓撲優化設計。