施工參數對心墻礫石土滲透系數影響研究

張返成

(吉安市螺灘水利水電中心，江西 吉安 343060)

滲透系數可反應心墻堆石壩內部的滲流情況，該因素對大壩的力學性能及穩定性影響顯著，近年來，許多專家學者針對心墻內部滲流情況開展相關研究。

張超萍等人[1]基于監測數據，對某心墻堆石壩的滲流情況進行監測，分析不同防滲效果對其滲流情況的影響，結果表明，防滲墻的防滲效果最好。許云鵬等人[2]基于土壤水分特征曲線，建立心墻堆石壩的滲流模型，分析該模型預測其滲漏系數的精度，結果表明，該模型可準確反應大壩內部的滲流情況，準確性較高。丁艷輝等人[3]對某水庫大壩的滲流及變形規律進行監測，分析大壩頂部發生不均勻沉降的原因，結果表明，大壩內部滲流會導致壩頂變形，但是大壩總體穩定性及安全性較高。王芳等人[4]結合正交試驗與數值模擬，分析庫水位變化條件下，某心墻堆石壩的變形及滲流規律，結果表明，大壩變形與心墻內部的滲流情況有關，且與滲透系數呈正比。楊啟貴等人[5]以某瀝青混凝土心墻堆石壩為研究對象，對其壩體的滲流及穩定性進行計算，并分析動、靜荷載下壩體的變形情況，并依據計算結果，對大壩進行設計，為后續滲流控制提供相關參考依據。

本研究以某水利工程的心墻堆石壩為研究對象，基于鯨魚優化算法，構建滲透系數預測模型，分析各種因素對滲透系數的影響。

1 工程概況

本研究以某水利工程為研究對象，工程由大壩樞紐、供水工程兩部分組成，大壩為面板堆石壩，防滲體為礫石土直心墻，最大壩高63.0m，壩頂高程1668.0m，壩軸線長121.84m。流域地處第二地形階梯帶，地貌屬高原中山溝谷地貌類型，地下水由大氣降雨及地表徑流的補給，通過脈狀流和巖溶管道流形式往低處排泄，最終呈分散狀或集中形式排出地表補給下游河流。庫區為溝谷地形，出露地層為峨眉山玄武巖組(P2β)的碎屑巖地層及第四系覆蓋層，該地區不良物理地質現象總體發育較弱，主要表現為風化、岸坡卸荷、第四系堆積體等，分布在河流、溝谷兩岸緩坡及坡腳地帶。

2 滲透系數預測模型構建

本研究基于鯨魚優化算法，構建滲透系數預測模型，分析各種因素對滲透系數(k)的影響，其目標函數如式(1)所示。

k=f(Cu，Cc，D5，D0.075，w，N0，N1，N2，H)

(1)

式中，Cu—不均勻系數；Cc—曲率系數；D5—粒徑大于5mm顆粒質量分數，%；、D0.075—粒徑小于0.075mm顆粒質量分數，%；w—含水率，%；Ni—碾遍次數，次；H—壓實厚度，m。

采用最大信息系數(MIC)分析式(1)中參數對滲透系數的影響，其計算公式如式(2)所示。

(2)

式中，p—聯合概率；I—互信息。

為分析不同參數對心墻礫石土滲透系數的影響，分別選取9組數據，對滲透系數進行預測，其輸入參數見表1。

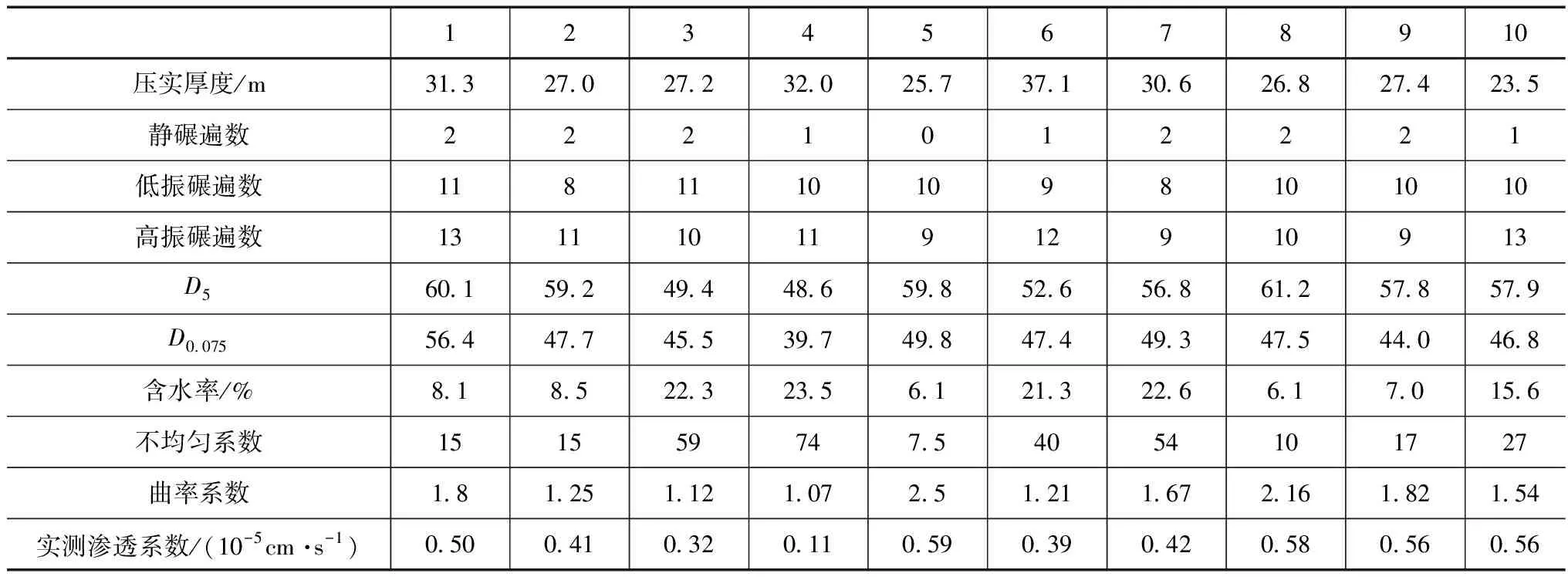
表1 輸入參數

3 結果分析

BPNN模型和WOA-SVM模型是鯨魚優化算法中兩種常見的訓練算法，為選取合適的算法模型對滲透系數預測模型進行訓練，采用BPNN模型和WOA-SVM模型對滲透系數預測模型進行訓練，并將其預測值與實際值進行對比，采用BPNN模型得出的測試樣本編號-滲透系數曲線如圖1所示。

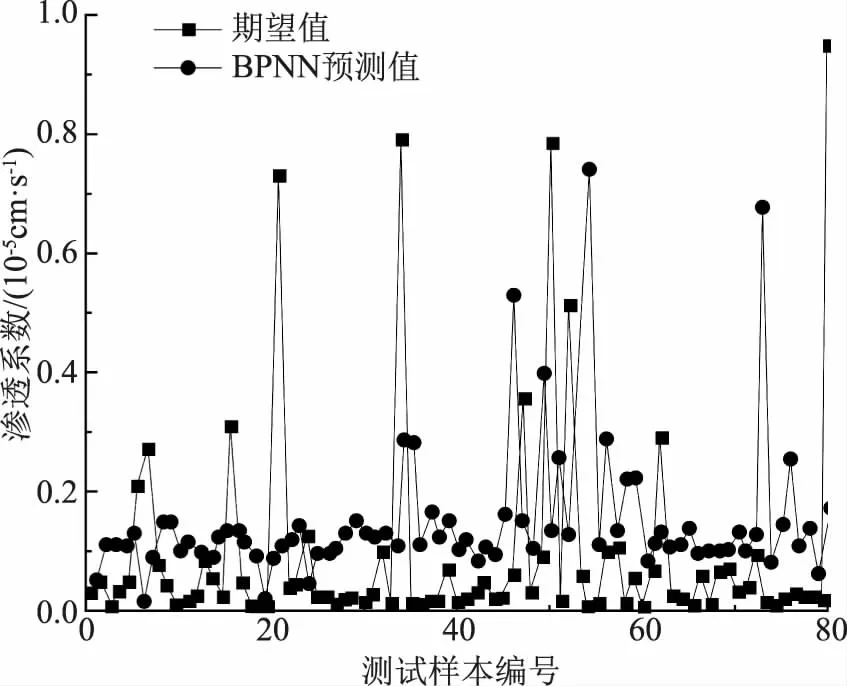
圖1 BPNN模型的測試樣本編號-滲透系數曲線

由圖1可知，采用BPNN模型得出的滲透系數波動范圍范圍較大，其值集中于0～0.8×10-5cm/s間，滲透系數實際值的波動范圍在0～1.0×10-5cm/s間，二者間的最大誤差為0.7×10-5cm/s，最小誤差小于0.01×10-5cm/s，說明采用該模型對滲透系數預測模型進行訓練的效果較好，但預測值與實際值間仍存在一定的差異，預測精度存在改進的空間。

采用WOA-SVM模型得出的測試樣本編號-滲透系數曲線如圖2所示。

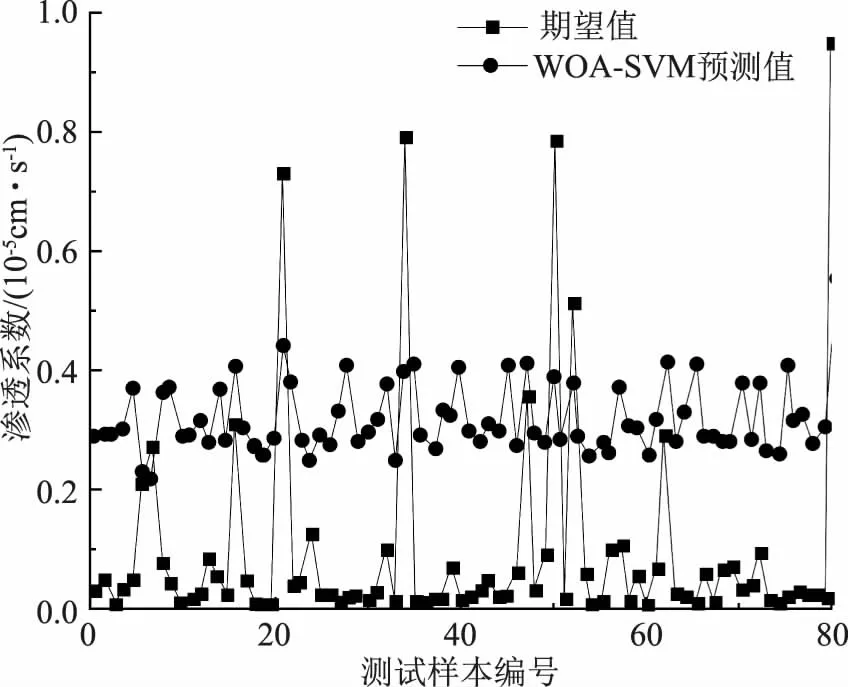
圖2 WOA-SVM模型的測試樣本編號-滲透系數曲線

由圖2可知，采用WOA-SVM模型得出的滲透系數預測值波動范圍較小，其滲透系數集中于0.2×10-5cm/s～0.4×10-5cm/s，采用WOA-SVM模型得出的滲透系數大多大于滲透系數實際值，二者間的滲透系數最大差值為0.4×10-5cm/s，滲透系數最小差值小于0.02×10-5cm/s，說明采用WOA-SVM模型對滲透系數進行預測的準確性良好。綜合以上分析可得，采用WOA-SVM模型訓練得出的滲透系數較為穩定，其波動范圍較小，但是其預測精度劣于BPNN模型；采用BPNN模型訓練得出的滲透系數波動性較大，但是其滲透系數預測結果與實際值間的差值較小；以上兩種模型對于心墻礫石土的滲透系數的預測效果及精度良好，且各有優勢，但是其預測精度仍存在可以改進的空間，為進一步提高滲透系數預測效果和預測精度，可以結合BPNN模型和WOA-SVM模型對滲透系數預測模型進行訓練。

根據以上分析可得，結合BPNN模型和WOA-SVM模型可提高滲透系數預測的準確性，為進一步提高滲透系數預測效果和預測精度，對比分析BPNN模型和WOA-SVM模型結合得出的滲透系數預測結果與滲透系數實際值間的差異，測試樣本編號-滲透系數曲線如圖3所示。

由圖3可知，采用BPNN-WOA-SVM模型得出的滲透系數預測值與實際值間的差值較小，且二者間的測試樣本編號-滲透系數曲線變化趨勢具有一致性，預測值與實際值間的最大差值為0.15×10-5cm/s，對比僅使用BPNN模型和WOA-SVM模型訓練的滲透系數預測結果可得，結合2種模型進行預測誤差減小了0.25×10-5cm/s～0.55×10-5cm/s，且預測結果較為穩定，BPNN-WOA-SVM模型對滲透系數預測的準確性提升效果顯著。

為直觀反映BPNN-WOA-SVM模型對滲透系數的預測效果，對采用不同模型預測的結果進行誤差分析，誤差分析結果見表2。

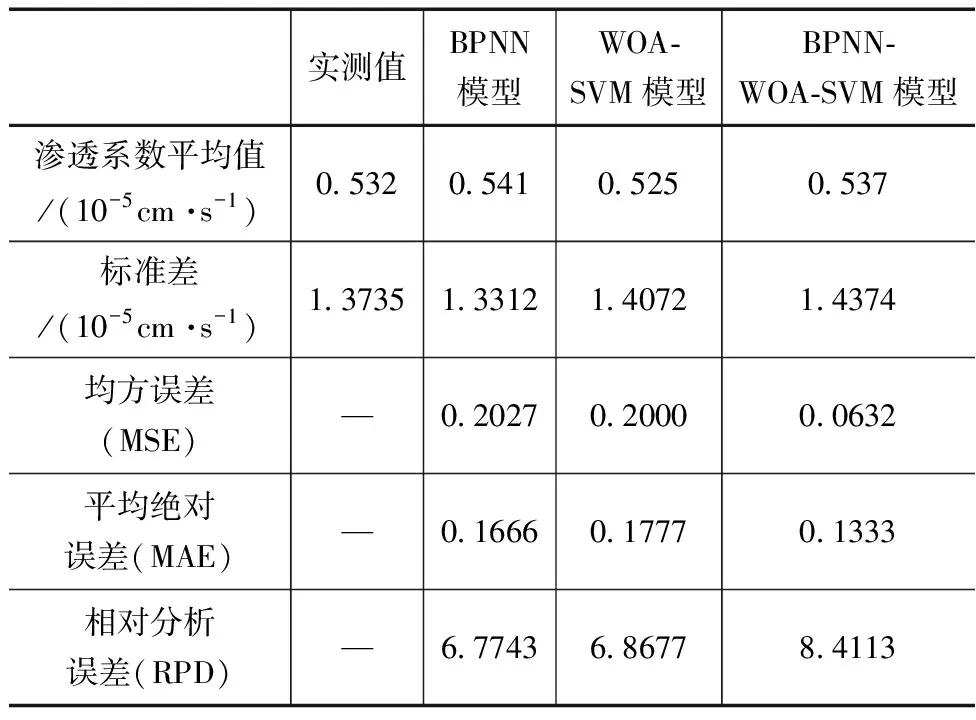
表2 誤差分析結果

由表2可知，采用BPNN-WOA-SVM模型預測得出的滲透系數平均值與實測值間的差值最小，二者間的差值僅為0.5×10-7cm/s。通過不同模型的誤差分析可得，BPNN-WOA-SVM模型的均方誤差與平均絕對誤差有最小值，說明采用該模型的預測準確性較高。采用3種模型得出的相對分析誤差均大于2，說明以上模型的穩定性好，能夠達到實際應用標準，其中，BPNN-WOA-SVM模型的相對分析誤差最大，該模型的預測效果最好。

根據以上分析可得，采用BPNN-WOA-SVM模型對心墻礫石土的滲透系數進行預測的效果較好，為分析碾壓施工參數對其滲透系數的影響，以表1所示的參數為研究對象，對滲透系數進行預測，將預測結果與不考慮碾壓施工參數的預測值進行對比，其樣本序號-滲透系數曲線如圖4所示。

圖4 樣本序號-滲透系數曲線

由圖4可知，不同碾壓參數下的心墻礫石土滲透系數具有一定的差異性，其中，樣本5的預測值最大，當考慮碾壓參數預測值時，滲透系數為0.61×10-5cm/s，樣本4的預測值最小，當考慮碾壓參數預測值時，其滲透系數為0.17×10-5cm/s。對比是否考慮碾壓參數下的心墻礫石土滲透系數可得，二者得出的滲透系數具有一定的差異性，其中，考慮碾壓參數的滲透系數預測值與實測值間的差值較小，說明考慮碾壓參數對心墻礫石土滲透系數進行預測更符合實際工程的情況，預測結果更加準確。

分析碾壓參數對各倉面的滲透系數影響，見表3。

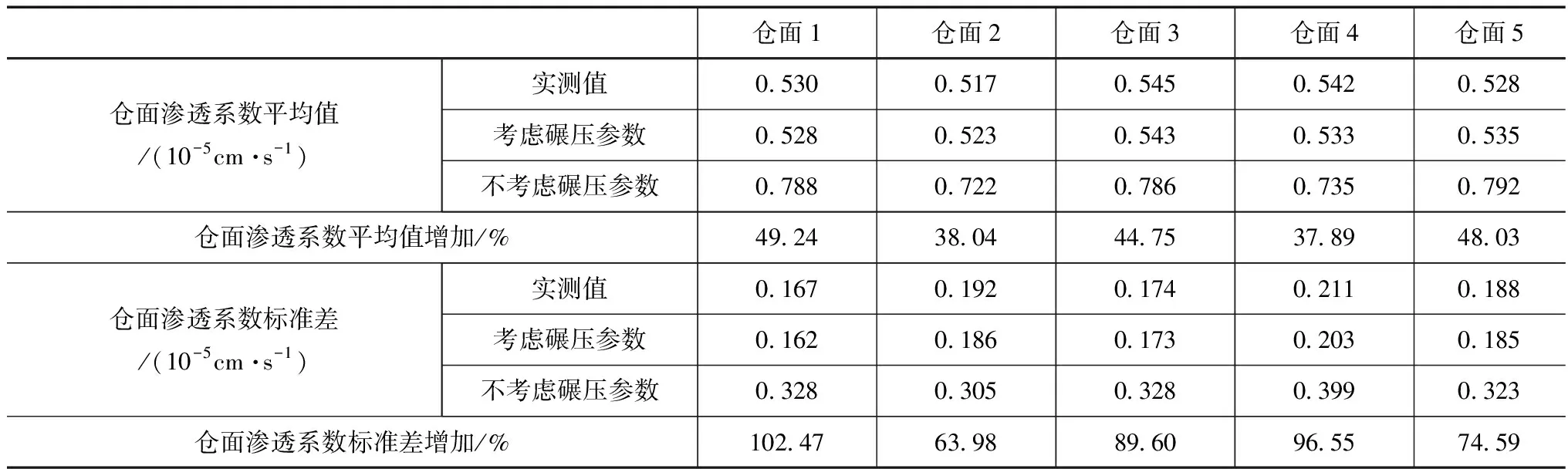
表3 碾壓參數影響結果

由表3可知，考慮碾壓參數的滲透系數與實測值間的差值較小，其中，倉面1與倉面3的預測精度最高，二者間的滲透系數平均值差值均為0.002×10-5cm/s，不考慮碾壓參數的預測精度較差，與實測值間的滲透系數差值均大于0.2×10-5cm/s，說明碾壓參數對心墻礫石土滲透系數的影響較大，為提高預測結果的準確性，應考慮碾壓施工參數對滲透系數的影響[6]。

以表1中的參數為研究對象，對考慮碾壓參數下的心墻礫石土滲透系數進行預測，對比不同模型下的預測結果，其樣本序號-滲透系數曲線如圖5所示。

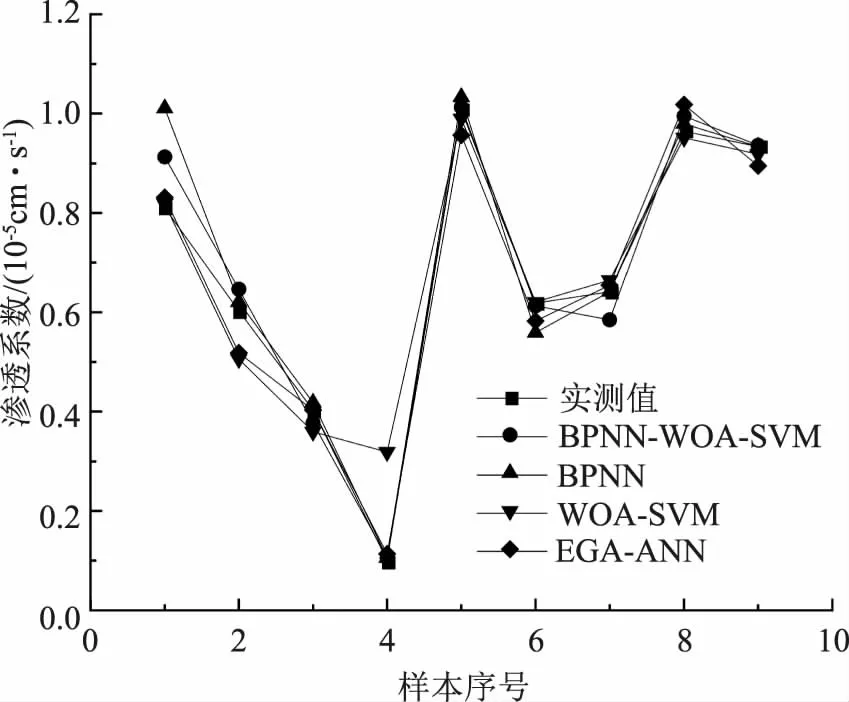
圖5 樣本序號-滲透系數曲線

由圖5可知，采用WOA-SVM模型得出的預測結果與實測值間的差值最大，說明采用該模型對心墻礫石土滲透系數進行預測的精度最低，采用BPNN-WOA-SVM模型得出的樣本序號-滲透系數曲線與實測值曲線的吻合度最高，說明采用組合模型可顯著提升心墻礫石土的滲透系數的預測精度。

4 結論

本文以某心墻堆石壩為研究對象，基于鯨魚優化算法，構建滲透系數預測模型，分析各種因素對滲透系數的影響，對比僅使用BPNN模型和WOA-SVM模型訓練的滲透系數預測結果表明，單一模型與組合模型的穩定性好，能夠達到實際應用標準，采用WOA-SVM模型得出的預測結果與實測值間的差值最大，精度最低，采用BPNN-WOA-SVM模型得出的樣本序號-滲透系數曲線與實測值曲線的吻合度最高，模型預測結果較為穩定，得出的滲透系數預測值與實際值間的差值較小，對滲透系數預測的準確性提升效果顯著。施工參數對心墻礫石土滲透系數的影響較大，為提高預測結果的準確性，應考慮碾壓施工參數對滲透系數的影響。