改進深度神經網絡的用戶用電量預測方法

蔡翔 朱莉

[摘 要]針對深度神經網絡對電能預測精度低的問題，提出正弦粒子群優化神經元數量的深度神經網絡算法，通過對粒子群算法進行變異操作和慣性權重改進，來對深度神經網絡隱藏層神經元參數進行尋優。實驗結果表明，SPSONN-DNN算法相比于DNN、極度梯度提升、線性回歸、兩種改進PSONN-DNN算法的預測精度分別提高了1.926%、2.820%、1.500%、0.633%、0.582%；SPSONN-DNN算法相比于兩種改進PSONN-DNN算法迭代次數分別減少6次、4次。

[關鍵詞]電量預測；深度神經網絡；粒子群算法；預測精度

[中圖分類號]TP391[文獻標識碼]A

電量預測是智能電網中電能調度的理論依據，提前通過預測模型來推測出各地區的用電量，使供電部門的輸電量和各地區的用電量達到供需平衡，從而減少電網中電能的浪費^[1]。隨著人工智能的興起，深度神經網絡由于具有自學習、自適應、容錯性等特點，大量的學者將其應用在電量預測領域，但是深度神經網絡處理不同領域的數據集時，由于數據的多樣性導致深度神經網絡的結構參數不同。人們利用其它算法的優點來對深度神經網絡的結構參數進行優化，但只是對神經網絡中的訓練數據、學習率、輸入權值等參數進行尋優，而隱藏層神經元數量是根據輸入參數隨機設置的，不是最佳的參數，導致網絡的模型達不到最優，模型預測精度較低^[2-3]。

優化算法能準確的對深度神經網絡各隱藏層神經元進行尋優，其典型方法有粒子群算法、遺傳算法、蟻群算法。又因粒子群算法相比于遺傳算法、蟻群算法需要調整的參數少、搜索速度快、效率高以及簡單容易實現等優點^[4-5]。本文利用改進粒子群算法來優化深度神經網絡各隱藏層神經元數量。

1 算法設計

1.1 SPSONN-DNN預測模型框架

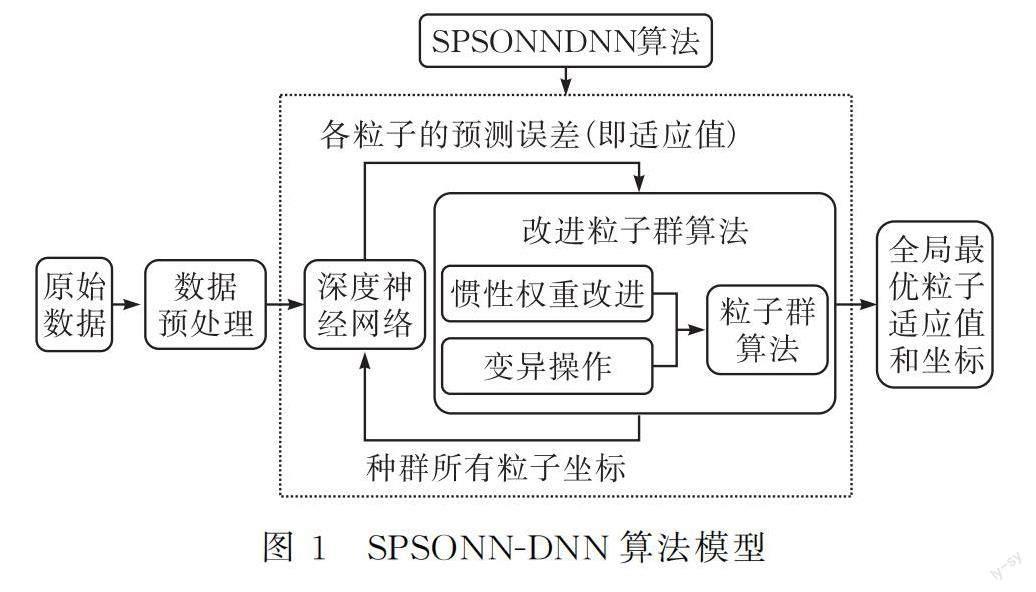
改進粒子群優化深度神經網絡的模型見圖1。

本文原始數據為某地區的家庭用電量數據，數據包括日期、時間、平均有功功率、平均無功功率、平均電壓、平均電流、3個計量表等9個維度的參數。

首先，對原始數據進行預處理。在數據預處理過程中，先將數據格式進行轉換，然后將數據的日期和時間轉換為浮點型，將各參數的單位換算統一；接著查找缺失、異常字符串的數據并將其刪除，因為是對家庭用電量進行短期預測，刪除對數據的整體沒有影響。

SPSONN-DNN算法是利用改進粒子群算法的種群粒子在迭代過程中的位置坐標來確定深度神經網絡隱藏層神經元數量，深度神經網絡根據每個粒子坐標來確定其對應的預測誤差（即適應值），粒子群算法從所有粒子中尋找出最優粒子，然后再根據粒子群的速度和位置更新公式來更新所有粒子，經過多次迭代后尋找出全局最優粒子，全局最優粒子坐標和適應值分別代表深度神經網絡隱藏層神經元的數量和相對應的預測誤差^[6]。

1.2 粒子群慣性權重的改進

粒子群算法是通過模擬鳥群覓食的行為而發展起來的一種基于群體協作的隨機搜索算法^[7-8]。

粒子群有兩個特性：速度和位置。速度大小決定下一次迭代后的位置變化大小；位置的維度是由所要解決的問題決定的，每個粒子的位置信息可以看成適應函數的一組解，每個粒子空間坐標的不斷變化，代表其函數解也是在不斷變化的。PSO算法中粒子的速度和位置公式如下：

式中，v^k_id表示粒子i第k次迭代的飛行速度的第d維分量；x^k_id表示粒子i第k次迭代的位置矢量的第d維分量；pbest_id表示粒子i第d維分量的局部（即個體）最優值；gbest_id表示粒子i第d維分量的全局（即群體）最優值；c₁、c₂表示學習因子；r₁、r₂表示取值范圍在[0，1]之間的隨機數；w表示慣性權重（非負數）。

通過對粒子群算法的分析可知，粒子群算法的搜索能力和收斂能力都與慣性權重w息息相關。根據分析，粒子群算法在尋優時，前期需要速度較大，從而提高全局搜索能力；中期需要速度適中，來平衡全局搜索能力和局部搜索能力；后期需要速度較小，使得局部搜索能力較強。

慣性權重為固定值已經很難滿足粒子群算法在尋優過程中全局搜索能力和局部搜索能力的轉換。很多學者提出了優化的方法，一般分為線性和非線性兩種方法：

式中，w是指慣性權重，w_max、w_min分別代表最大、最小慣性權重值，t_max表示種群的最大迭代次數，t表示種群的當前迭代次數。

公式（3）是線性變換，在粒子群算法迭代過程中慣性權重變化率相同，不能滿足粒子群算法在迭代前期慣性權重變化較小的要求；公式（4）是非線性變換，在粒子群算法迭代中期，變化仍然很小，不能很好平衡全局搜索能力和局部搜索能力。

為了使粒子群算法計算結果更加準確，提出了正弦慣性權重，使慣性權重隨著粒子的迭代次數而成正弦變換，滿足粒子群算法在整個迭代過程中全局搜索能力和局部搜索能力的轉換如下式：

式中，w表示慣性權重，w_max、w_min分別表示慣性權重的最大值和最小值，iter表示當前迭代次數，iter_max表示最大迭代次數。

1.3 粒子群陷入局部最優的改進

粒子群雖然對慣性權重進行了改進，但是在尋優的過程中，隨著種群聚合程度越來越高，種群也可能會匯聚于一點。發生這種情況的根本原因是種群在迭代尋優的過程中，其本身的多樣性逐漸降低，導致陷入局部最優。為了解決這個問題，引入種群平均距離來描述種群的離散程度，根據平均距離的大小和迭代誤差來判斷種群是否陷入局部最優。

式中，L（iter）表示種群在第iter次迭代的平均距離，N表示種群的粒子數，d表示粒子的維度，x_in（iter）表示第i個粒子的n維分量在iter次迭代的值，x-_n（iter）表示所有粒子在iter次迭代的平均坐標的n維分量的值。

當種群粒子平均距離L（iter）的值較大時，粒子分布程度較分散，PSO進行大范圍的全局搜索。隨著迭代的進行，L（iter）的值會逐漸減小，表示種群中粒子分布程度較密集，種群的多樣性也會降低，此時PSO易陷入局部最優，從而無法達到全局最優。

此時就需要變異操作來提高種群粒子的多樣性。給定閾值，如果種群粒子平均距離L（iter）的值低于設定閾值則表示PSO陷入局部最優，應啟動變異操作，將特定的粒子通過變異的方式增加種群活性，使其跳入到其它區域繼續尋優，讓種群達到全局最優。

可通過L（iter）的大小或粒子群全局最優值來判斷是否需要進行變異操作。若粒子經過多次迭代仍未發生明顯變化或A低于給定的閾值，則可進行變異操作。變異操作時根據粒子離全局最優的距離來選取變異操作的粒子，而變異前后粒子群的最優值保持不變。變異操作的公式如下：

式中，x′_i表示粒子i變異后的位置，x_i表示粒子i變異前的位置，iter是種群的當前迭代次數，iter_max是種群的最大迭代次數，N（0，1）表示0～1之間的任選隨機數。

1.4 算法流程

SPSONN-DNN算法流程如下：

1）初始化。對改進粒子群算法和深度神經網絡進行初始化設置，改進粒子群算法需要設置以下參數：粒子的數量N、粒子的維度D、算法的最大迭代次數iter_max、慣性權重的最大值w_max和最小值w_min以及兩個學習因子c₁和c₂；深度神經網絡需要設置迭代次數、隱藏層數等。

2）選取合適適應函數并計算適應值。根據具體問題，設計相關的函數關系，然后將粒子的信息輸入到函數關系中求出函數的輸出值（即適應值）。本文以深度神經網絡損失函數為參考，以均方根誤差公式作為適應度函數。

3）將初始的粒子位置參數作為DNN網絡各隱藏層的神經元個數，計算出預測誤差作為粒子群算法的適應值。各粒子的適應度值就是個體最優值，在個體最優值中尋找全局最優值。

4）慣性權重的更新。將種群當前迭代次數帶入式（5）中，計算出新的慣性權重值。

5）更新種群各粒子的速度和位置。根據式（1）、式（2）來更新每個粒子的速度和位置。

6）將更新后的各粒子分別帶入適應函數，計算出對應的適應值。

7）更新個體最優值。計算出各粒子適應值后，分別與各粒子的當前個體最優值作比較，若小于當前個體最優值，則將該粒子的適應值作為個體最優值，反之，個體最優值不變。

8）更新全局最優值。當個體最優值更新后，將各粒子的個體最優值依次與全局最優值作比較，若粒子個體最優值小于全局最優值，則將該粒子的個體最優值作為全局最優值，反之，全局最優值不變。

9）變異判斷。按照公式（6）計算得到的平均距離來判斷是否達到變異條件，如果距離低于給定的閾值或種群迭代多次全局最優值沒有發生明顯變化則執行步驟10）；否則執行步驟11）。

10）變異操作。選取部分平均距離較小的粒子，根據式（7）計算出變異后粒子位置。

11）結束循環判斷。當迭代次數或者最優適應值滿足種群要求后，則執行步驟12），否則執行步驟4）。

12）算法結束。輸出算法計算的最優值。

SPSONN-DNN算法流程如圖2所示。

2 算例分析

為驗證預測方法的有效性，選用網上公布的某一地區的用戶電量數據集。數據集包含平均有功功率、平均無功功率、平均電壓、平均電流等數據參數。

2.1 實例分析

選取用戶的用電量數據（表1），進行數據分析、過濾。首先將數據的格式統一，單位換算成統一的標準；然后查找缺失、異常字符串的數據，接著剔除異常數據或填補缺失數據；最后將處理好的數據集作為DNN、SPSONN-DNN等算法的數據集，以有功功率為輸出，其它參數為輸入。

2.2 實驗參數設置

由式（2）、式（6）可知，需要初始化設置的實驗參數有粒子的數量N、粒子的維度D、算法的最大迭代次數iter_max、慣性權重的最大值w_max和最小值w_min以及兩個學習因子c₁和c₂。本文將N設置為50、D設置為6、iter_max設置為30，w_max設置為0.9、w_min設置為0.4、c₁和c₂都設置為0.2；深度神經網絡隱藏層數設為6，各隱藏層神經元的數量根據全局最優粒子坐標值來確定。

2.3 實驗結果與分析

深度神經網絡、線性回歸、極限梯度提升、兩種改進 PSONN-DNN算法以及SPSONN-DNN算法分別以處理好的數據集來訓練和預測用戶用電量，預測結果見圖3-9，本文以MAPE和MSE為標準對算法的精度進行衡量。

圖3為深度神經網絡的真實值與預測值誤差曲線，其中藍色曲線代表真實數據集，紅色曲線表示預測數據集，MAPE為5.997%，說明訓練數據集的預測值與真實值之間的平均絕對百分比誤差為5.997%；MSE為0.3673，說明訓練數據集的預測值與真實值之間的均方誤差為0.3673。

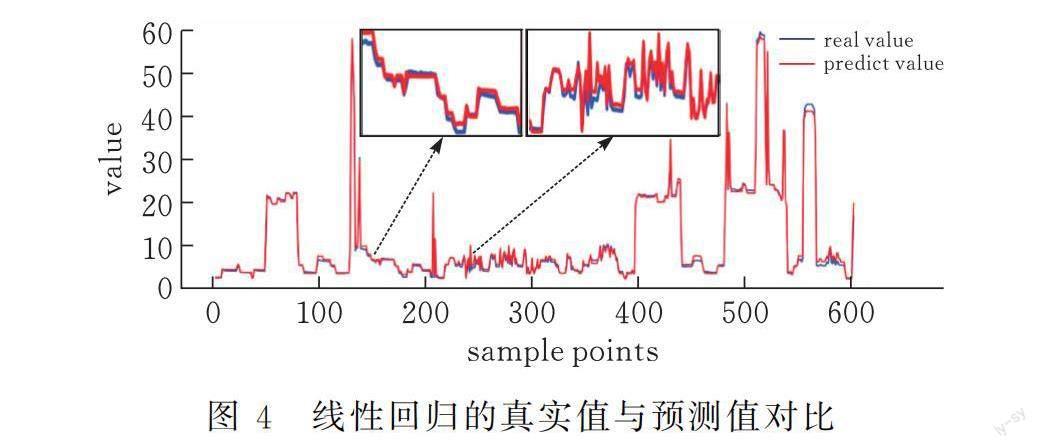
圖4表示線性回歸的真實值與預測值的對比曲線圖，圖中橫坐標表示樣本點的個數，縱坐標表示每個樣本點的數值，其中藍色曲線代表真實數據，紅色曲線表示預測數據。計算可知，MAPE為6.871%，即訓練數據集的預測值與真實值之間的平均絕對百分比誤差為6.871%；MSE為0.5717，即訓練數據集的預測值與真實值之間的均方誤差為0.5717。

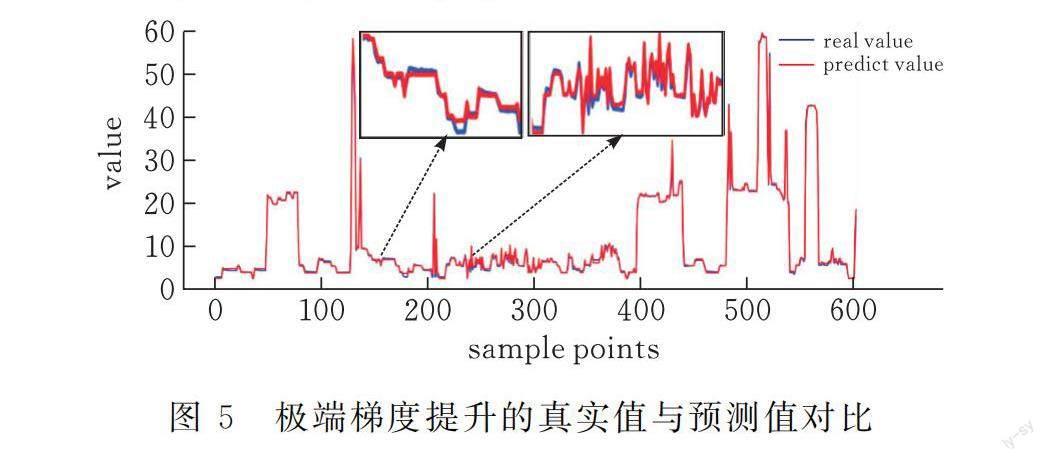
圖5表示極端梯度提升的真實值與預測值對比曲線圖，圖中橫坐標表示樣本點的個數，縱坐標表示每個樣本點的數值，其中藍色曲線代表真實數據，紅色曲線表示預測數據。計算可知，MAPE為5.551%，說明測試數據集的預測值與真實值之間的平均絕對百分比誤差為5.551%；MSE為0.3232，說明訓練數據集的預測值與真實值之間的均方誤差為0.3232。

本文對粒子群優化神經元數量的深度神經網絡算法中的慣性權重分別做線性變換、微分變換、正弦變換，如式（3）、（4）、（5）所示。圖6中PSONN-DNN（method1）表示慣性權重為線性變換；PSONN-DNN（method2）表示慣性權重為微分變換；SPSONN-DNN表示慣性權重為正弦變換。

圖6a沒有設置粒子群算法的適應值閾值，可知PSONN-DNN（method1）算法的適應值（即MAPE）為4.693%，是指PSONN-DNN（method1）算法的全局最優粒子的適應值為4.693%，全局最優粒子位置為（30，15，55，27，27，13）；PSONN-DNN（method2）算法的適應值為4.622%，是指PSONN-DNN（method2）算法的全局最優粒子的適應值為4.622%，全局最優粒子位置為（54，51，45，29，3，44）；SPSONN-DNN算法適應值為4.103%，是指SPSONN-DNN算法的全局最優粒子的適應值為4.103%，全局最優粒子位置為（58，15，54，34，53，33）。因此，相比于其它兩種算法，SPSONN-DNN算法預測精度有所提升。

圖6b設置粒子群算法的適應值為4.9%，PSONN-DNN（method1）算法在迭代13次后達到4.9%；PSONN-DNN（method2）算法在迭代11次后達到4.9%；SPSONN-DNN算法在迭代7次時適應值達到了4.9%。因此，相比于其他兩種算法，SPSONN-DNN算法迭代次數均減少了。

將PSONN-DNN（method1）算法、PSONN-DNN（method2）算法以及SPSONN-DNN算法的全局最優粒子坐標帶入深度神經網絡中檢驗其準確性。

圖7表示PSONN-DNN（method1）算法的迭代次數與訓練誤差曲線圖，圖中橫坐標表示樣本點的個數，縱坐標表示每個樣本點的數值，其中藍色曲線代表真實數據，紅色曲線表示預測數據。計算可知，MAPE為4.684%，即PSONN-DNN（method1）算法中訓練數據集的預測值與真實值之間的平均絕對百分比誤差為4.684%；MSE為0.2853，表示PSONN-DNN（mothed1）算法中測試數據集的預測值與真實值之間的均方誤差為0.2853。

圖8表示PSONN-DNN（method2）算法的迭代次數與誤差曲線圖，圖中橫坐標表示樣本點的個數，縱坐標表示每個樣本點的數值，其中藍色曲線代表真實數據，紅色曲線表示預測數據。計算可知，MAPE為4.633%，表示PSONN-DNN（method2）算法中訓練數據集的預測值與真實值之間的平均絕對百分比誤差為4.633%；MSE為0.2846，表示PSONN-DNN（method2）算法中測試數據集的預測值與真實值之間的均方誤差為0.2846。

圖9表示SPSONN-DNN算法的迭代次數與誤差曲線，圖中橫坐標表示樣本點的個數，縱坐標表示每個樣本點的數值，其中藍色曲線代表真實數據，紅色曲線表示預測數據。計算可知，MAPE為4.051%，表示SPSONN-DNN算法中訓練數據集的預測值與真實值之間的平均絕對百分比誤差為4.051%；MSE為0.2647，表示SPSONN-DNN算法中測試數據集的預測值與真實值之間的均方誤差為0.2647。

綜上所述，驗證了PSONN-DNN（method1）算法、PSONN-DNN（method2）算法以及SPSONN-DNN算法的準確性。

由表2、表3可知，SPSONN-DNN算法的預測精度（MAPE）相比于DNN、線性回歸、極限梯度提升分別提升了1.926%、2.820%、1.500%；并且SPSONN-DNN算法相比于PSONN-DNN（mothed1）算法、PSONN-DNN（mothed2）算法預測精度（MAPE）分別提升了0.633%、0.582%，迭代次數分別減少了6次、4次。實驗證明，相比于傳統的方法，SPSONN-DNN算法在用戶電量預測中預測精度更高。本文方法在電量預測中具有普遍的適用性。

3 結論

目前，深度神經網絡應用廣泛，但是面對不同領域的數據集，深度神經網絡隱藏層神經元參數不確定。針對這一問題，提出改進粒子群優化神經元數量的深度神經網絡算法對家庭用電進行預測，該算法是將粒子群中的慣性權重改進為隨迭代次數變化而成正弦變化的變量；同時在計算中加入了變異操作，使陷入局部最優的粒子跳入其它區域繼續尋優。通過實驗驗證，SPSONN-DNN算法相比于DNN、線性回歸、極限梯度提升方法的預測精度（MAPE）分別提升了1.926%、2.820%、1.500%，同時相比于PSONN-DNN（mothed1）算法、PSONN-DNN（mothed2）算法的預測精度分別提升了0.633%、0.582%，并且迭代次數分別減少了6次、4次。因此，通過SPSONN-DNN算法可以提高電量的預測精度，以此來減少發電量，從而減少能源的浪費。

[ 參 考 文 獻 ]

[1] GYAMFI S， KRUMDIECK S. Scenario analysis of residential demand response at network peak periods[J]. Electric Power Systems Research， 2012， 93（01）：32-38.

[2] KUN XIE， HONG YI， GANGYI HU， et al. Short-term power load forecasting based on Elman neural network with particle swarm optimization[J]. Neurocomputing， 2019， 416（11）： 136-142.

[3] GUNDU V， SIMON S P. PSO-LSTM for short term forecast of heterogeneous time series electricity price signals[J]. Journal of Ambient Intelligence and Humanized Computing， 2020， 12（02）： 2375-2385.

[4] YIN L， SUN Z， GAO F， et al. Deep forest regression for short-term load forecasting of power systems[J]. IEEE Access， 2020， 8：49 090-49 099.

[5] NIU D， SHI H， LI J， et al. Research on short-term power load time series forecasting model based on BP neural network[C].∥2010 2nd International Conference on Advanced Computer Control， 2010.

[6] 郭海燕， 李英娜， 李川. 基于模擬退火算法優化BP的短期負荷預測控制策略[J]. 陜西理工大學學報， 2021， 37（01）： 36-42.

[7] YLDZ C， AKGZ H， KORKMAZ D. An improved residual-based convolutional neural network for very short-term wind power forecasting[J]. Energy Conversion and Management， 2021， 28（01）： 113731.

[8] 楊毅， 雷霞， 徐貴陽， 等. 采用PSO-BF算法的微電網多目標電能優化調度[J].電力系統保護與控制， 2014， 42（13）： 13-20.

Research on User Electricity Consumption Prediction Method

Based on Improved Deep Neural Network

CAI Xiang¹，ZHU Li²

（1 School of Electrical and Electronic Engineering， Hubei Univ. of Tech.，Wuhan 430068， China；

2 Hubei Provincial Key Laboratory of Solar Energy Efficient

Utilization and Energy Storage Operation Control，

Hubei Univ. of Tech.， Wuhan 430068， China）

Abstract：With the rise of artificial intelligence， researchers have widely used deep neural networks in the field of electric power. However， due to the uncertainty of the parameters of neurons in the hidden layer of deep neural networks， the prediction accuracy of electric power is low， resulting in an imbalance between the supply and demand of electric power and in power redundancy. To this end， we propose the Sin Particle Swarm Optimization Number of Neurons of Deep Neural Networks （SPSONN-DNN） algorithm， which is based on the mutation operation and inertia weight of the particle swarm algorithm improvement， to optimize the parameters of the hidden layer neurons of the deep neural network. The experimental results show that compared with DNN， extreme gradient boosting， linear regression， and the two improved PSONN-DNN algorithms， the prediction accuracy of the SPSONN-DNN algorithm is improved by 1.926%， 2.820%， 1.500%， 0.633%， and 0.582%， respectively; Compared with the two improved PSONN-DNN algorithms， the DNN algorithm reduces the number of iterations by 6 and 4 times， respectively.

Keywords：power prediction; deep neural network; particle swarm optimization; prediction accuracy

[責任編校：張巖芳]