基于機會約束的園區綜合能源系統優化調度
付波 鄧競成 康毅恒
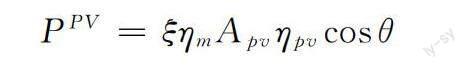
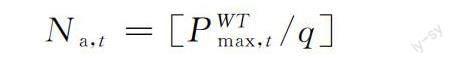

[摘 要]基于機會約束理論應對可再生能源的不確定性,構建了考慮不確定性的園區綜合能源系統優化調度模型。同時針對引入機會約束后所建立的隨機優化問題,通過序列運算理論對機會約束進行確定性轉化,降低了求解的復雜度,并調用CPLEX對轉換后得到的混合整數線性規劃模型進行求解。算例仿真驗證了該模型和方法的可行性,同時在穩定性和求解速度方面較啟發式算法有所提升。
[關鍵詞]機會約束;序列運算;需求響應;園區綜合能源系統
[中圖分類號]TM73[文獻標識碼]A
園區綜合能源系統根據能源間的互補特性以及能量梯級利用原則,對系統進行協調優化,是提高可再生能源消納率的重要途徑[1-2]。隨著PIES的發展和雙碳目標的提出,可再生能源接入比例不斷增加,其帶來的不確定性為優化調度帶來了較大的難度[3-4]。當下有兩種考慮可再生能源不確定性的主流方法:魯棒優化[5-6]和隨機優化[7-9]。
相比較而言,采用機會約束方法進行優化調度能取得某特定需求下的最優調度方案[10-12]。本文提出了一種基于機會約束的PIES優化調度方法。首先,建立各設備模型;其次,利用序列運算方法將可再生能源出力離散為概率性序列;再將含機會約束的調度問題轉換為混合整數規劃問題(Mixed Integer Linear Programing, MILP);最后通過YALMIP[13]調用CPLEX進行求解。通過算例仿真,驗證了本文方法的可行性及有效性。
1 園區綜合能源系統建模
本文構建的園區綜合能源系統(PIES)是電熱耦合系統,園區內電能由風機、光伏陣列上級電網供給,熱能由電鍋爐和儲熱設備供能。
1.1 風機出力模型
風機出力的不確定性主要來源于風速固有的間歇性、隨機性。先前的研究表明,風速服從Weibull分布,風速的概率密度函數
fw(v)=(k/γ)(v/γ)k-1exp[-(v/γ)k]
式中:v為實際風速;k為形狀系數,描述了風速概率密度函數的形狀;γ為尺度系數,反映了某時段的平均風速,由風速的概率密度函數可以推導出風機出力的概率密度函數。
1.2 光伏出力模型
光伏發電的輸出功率主要取決于太陽輻照度、環境溫度和組件本身特性等。統計研究顯示,一天中的太陽輻照度近似服從Beta分布,光伏輸出功率與太陽輻射強度的關系
式中:ξ為太陽輻照強度;ηm為最大功率跟蹤點;Apv為光伏組件輻射面積;ηpv為光伏板能量轉換系數;θ為太陽光入射角。光伏輸出功率與太陽輻照度呈線性關系,因此光伏輸出功率一般也服從Beta分布,可以推導出光伏輸出功率的概率密度函數。
1.3 需求響應模型
需求響應利用可控負荷作為靈活性資源參與電力系統的調峰。可時移負荷通過實時調度來實現系統供需平衡,但需確保調節總量不變。可中斷負荷是在用戶體驗尚可的前提下,對負荷功率進行一定削減的柔性負荷。本文需求響應模型描述如下:
式中:PLoad0為初始負荷;PLoadt為進行需求響應后的負荷;PTSLt為可時移負荷時移功率,δTSL為可時移負荷占總負荷比例;PITt為可中斷負荷中斷功率,δIT為可中斷負荷占總負荷比例。
2 綜合能源系統優化調度模型
2.1 目標函數
接入風電及光伏后,為避免出力偏差帶來的能量短缺,需要調用電網及儲能作為備用。PIES的運行成本由以下三個部分組成:電網購電成本、備用服務成本、儲能折舊成本。
式中:at為電網分時電價,PEVt為t時段電動汽車消耗的電網電量,PEBt為t時段電鍋爐的耗電功率,b為電網備用價格,Rgridt為電網提供的備用容量,c為電儲能備用價格,RESSt為電儲能提供的備用容量,d為電儲能折舊成本,PESSCH,t為t時段電儲能充電功率。
2.2 約束條件
2.2.1 系統運行約束
式中:k=EV,grid,EB分別表示電動汽車充放電功率、電網交互功率、電鍋爐功率;HEBt為電鍋爐的供熱功率;ηEB為電鍋爐電熱轉換系數。
2.2.2 系統功率平衡約束
式中:E(PtDG)為分布式電源出力的期望值;PGLt為t時段不可時移負荷,PLoadt為t時段剩余電負荷;HLoadt為t段熱負荷需求,PHSSDC,t為t時段放熱功率,PHSSCH,t為t時段蓄熱功率。
2.2.3 儲能約束 本文中涉及的儲能設備有電熱儲能,儲能系統能夠實現能量的存取,需要確保儲能的充放不超過限制,儲能系統約束可建模為:
式中:PCH,t和PDC,t分別為t時段儲能充放電功率,Ct為t時段儲能容量,ηch、ηdc分別為充放效率;式(17)為電儲能提供的備用容量約束。
2.2.4 旋轉備用約束 本文中通過電儲能及電網提供備用服務,表示如下:
式中:PWTt、PPVt分別為風機及光伏的實際出力。
3 基于序列運算的綜合能源系統機會約束優化調度方法
3.1 機會約束的建立
為確保PIES的安全穩定運行,需要向系統內添加系統備用約束。由于備用約束中含可再生能源出力的隨機變量,可將其作為隨機優化問題建立機會約束。以系統備用容量滿足一定置信水平作為約束,出讓部分可靠性以降低系統備用需求,所建立的機會約束如下:
式中:Prob{}為概率計算算子,α為系統置信水平。由于基于機會約束中建立的約束中包含隨機變量,模型將無法進行直接求解,通常采用的求解方法為隨機模擬法,但該方法需要進行大量的比對運算,降低了模型的求解效率。
3.2 基于序列運算的機會約束確定性轉化
3.2.1 序列運算的基本規則 假設有長度為Na的離散概率性序列a(i)及長度為Nb的離散概率性序列b(i),其有以下幾個特征及運算方法:
式中:E(a)為序列a(i)的期望值;⊕為卷和符號;gs1(i)為卷和運算得到的概率序列。結合電力系統不確定性的實際需求,以風機為例,風機出力的概率序列長度可以通過下式計算:
式中:[]為向下取整,q為離散化步長,PWTmax,t為t時刻最大出力。風機概率性序列見表1。
光伏出力的概率性序列求取流程同上。由于風光出力的不確定性相互獨立,可通過式(3)將風電及光伏出力的序列進行卷和,得到聯合出力的概率性序列用于后續求解流程中。
3.2.2 機會約束轉換過程 為了將式(2)轉換為便于求解的確定性約束,需要提前獲取式中隨機變量PWTt+PPVt的分布及其逆函數,當隨機變量分離后,可采用解析法進行確定性轉換:
式中:φ為隨機變量ξ的概率分布函數,φ-1為φ的逆函數。由式(4)所列形式的概率密度函數形式, 其逆函數難以求解,轉換過程中也可能出現非唯一解。本文基于序列對概率分布進行離散化處理,風光聯合出力的概率性序列通過卷和運算求得,同時引入0-1輔助變量Zua,t,可以將機會約束轉化為確定性約束,該變量滿足以下兩個公式:
式中,σ為數值較大的正數,備用容量大于可再生能源可能的出力變化時,等價于1/σ≤Zua,t≤1+1/σ,由于Zua,t為0-1變量,此時只能取1;總備用容量小于可再生能源可能的出力變化時,等價于-1/σ≤Zua,t≤1-1/σ,此時只能取0,可用式(4)-(6)替代式(1)。至此,含有機會約束的優化調度模型被轉化為了MILP模型。
4 算例分析
4.1 算例參數
為驗證模型及方法的可行性,以某園區綜合能源系統為具體算例進行分析。表2為該園區所接入電網的分時電價;圖1為園區可再生能源出力期望值及電熱負荷。
電網提供的最大功率500 kW,備用價格0.04元/kWh;風機切入風速3 m/s,額定風速15 m/s,切出風速25 m/s,額定功率300 kW;光伏板能量轉化系數0.093,組件輻射面積1200 m2,最大功率110 kW;電儲能初始容量32 kW·h,最大容量160 kW·h,充放效率0.9,最大充放功率50 kW,折舊價格0.1元/kWh;熱儲能最大容量160 kW·h,最大充放功率60 kW;電鍋爐功率320 kW,轉換系數0.99;電動汽車調度周期內總功率為900 kW。
4.2 PIES最優調度策略
設置離散化步長為10 kW,置信度為90%,求得的調度方案運行成本為2527.52元,調度方案如圖2所示。
從圖2可以看出,熱儲能得到了充分的利用,電儲能出力較少的原因是用于承擔系統備用。同時可以發現,電動汽車充電及向電網購電均集中在低電價時段,提高了PIES系統運行的經濟性。此外,系統的棄風棄光功率始終為0,表示可再生能源被PIES系統完全消納,沒有產生棄風棄光現象。
4.3 需求響應對PIES的影響
需求響應具有協調電源及負荷的特性,能夠增強對新能源的消納能力。圖3為需求響應前后的負荷變化。從圖3中可以看出,需求響應對電負荷曲線有明顯的削峰填谷作用,結合分時電價曲線,可以看出調度計劃將高電價時段的可時移負荷轉移到了低電價時段,提高了PIES的經濟性;可中斷負荷在中高電價時段中斷,進一步提高了PIES的經濟性。
4.4 可再生能源不確定性分析
為了驗證該方法能夠通過人為設定置信水平在可靠性與經濟性中達到平衡,選取了5個不同置信水平進行模擬,得到不同置信水平下PIES備用及運行成本(圖4、表3)。
圖4為不同置信水平下PIES的備用需求,隨著置信水平的提高,運行可靠性提高,同時備用增加導致經濟性降低;反之,經濟性提高,可靠性降低。因此,合適的置信水平能夠實現PIES系統在經濟性和可靠性間的均衡。

