Optimal driving field for multipartite quantum battery coupled with a common thermal bath

Z Q Yang(楊梓騫), L K Zhou(周立坤), Z Y Zhou(周正陽),G R Jin(金光日), L Cheng(程龍), and X G Wang(王曉光)

1Physics Department,Zhejiang Sci-Tech University,Hangzhou 310018,China

2Zhejiang Institute of Modern Physics,Department of Physics,Zhejiang University,Hangzhou 310027,China

Keywords: quantum mechanics,thermodynamics

1.Introduction

Quantum batteries (QBs) are the simplest quantum systems that store and provide energy using quantum coherence and quantum entanglement in charging processes.[1–5]Starting from original ideas developed in Refs.[6,7],various quantum systems have been considered as candidates of QBs, including collective spins,[8,9]interacting spin chains,[10,11]collision model,[12–15]and mechanical flywheels.[16,17]Recently, Ferraroet al.[18]proposed a charging model of finite-Ntwo-level atoms via collectively interacting with a single cavity mode(known as the so-called Dicke QB).Many-body entanglement created by the common cavity model leads to the quantum advantage in the charging power in comparison with that of charging of each atom by each sperate cavity mode.[18]Collective charging QBs have been proposed in cavity and waveguide QED setups,[19–22]and most recently demonstrated by using fluorescent organic molecules in a microcavity.[23]

Using a static drving[6,10,24–26]and a harmonic driving field[18–20,27]as the charger, one can also realize a semiclassical Dicke model(i.e.,the so-called multipartite quantum battery), where quantum correlations among the spins can be achieved by coupling with a common thermal bath.Without the presence of the bath,Zhanget al.[28]have proposed finite-Ntwo-level atoms as a large-spin battery and the harmonic field as a charger.Analytical solutions has been derived to obtain the maximum stored energy in the battery.[28]Most recently, Changet al.[29]further investigated the collective interaction of the atoms with the common thermal bath.Due to the presence of the harmonic driving field and the bath, they find that the free energy variation in the steady state increases non-monotonically and reaches the maximal value at an optimal number of atomsNopt.This result is somewhat counterintuitive,since the stored energy should increase withN.

Here we investigate the setup of the QB similar to Changet al.[29]by considering a continuous-wave driving field(equivalently,the harmonic driving field with a rotating-wave approximation).We adopt the so-called ergotropy to quantify the useful energy stored in the QB.[30]For the single-atom case(i.e.,the conventional charging protocol withN=1),analytical result of the increased energy is derived to compare with the ergotropy at the long-time limit(i.e.,the steady-state ergotropy).By maximizing the steady-state ergotropy,we obtain an optimal value of the driving-field strength, dependent on the temperature of the bath.Such an observation holds for the finite-Ncase.With a fixed driving strength,there exists the optimal number of atomsNopt.Similar to Changet al.,[29]it implies that there exists an optimal building block for the multipartite quantum battery.However, if we adopt the optimal driving field for eachN, we can show that both the increased energy and the ergotropy increase monotonically withN,as is expected.

2.Quantum battery system

Following Changet al.,[29]we consider a multipartite battery consisting ofNidentical two-level atoms,which is driven by a continuous-wave driving field with the frequencyω.The total Hamiltonian is described by a semi-classical Dicke model as follows:

Next,we consider all the QBs(or the spins)weakly coupled with a common thermal bath,which provides an average number of excitations(ω0)=1/(eβω0-1).For simplicity,we adopt the short-hand notation=(ω0).After the longtime interactions, all the spins will be prepared in the Gibbs thermal state ?ρ0,i.e.,

whereβ=1/(kBT)is the inverse temperature,kBis the Boltzmann constant, and theZdenotes the partition function.At the zero temperature (T=0), we have the mean number of excitations=0, the initial state corresponds to all the spins in the ground state|g〉,and thereforeE(0)=-Nω0/2.With a finite temperature(T/=0),we obtain

with ?σp=∑m εm|ψm〉〈ψm| being the so-called passive state.Here{|ψm〉}denotes the eigenvectors of ?HSand{εm}represents the eigenvalues of ?ρsorted in ascending orderεm+1≥εm.Note that the free energyF=E-S/βhas been used to quantify the useful energy stored in the battery (see e.g., Changet al.[29]), whereSis the entropy andβis the inverse temperature.Both of them obey the relationF ≥W,[30]with the equality holding forN →∞.[7,30]

3.Conventional charging protocol

Here,we first investigate the conventional charging protocol(i.e.,the case ofN=1).[29]For this case,the spin operators in the Hamiltonians become ?J+→?σ+=|e〉〈g|and ?Jz →?σz/2.In the interaction picture, dynamics of the battery can be described by a Lindblad master equation(see Appendix A)

Other parameters can be found in Appendix B.Note thatE(0) =ω0(a1+b1) =-ω0/(2χ), as mentioned above.In Fig.1(a),we show the increase energy ?E(t)againsttby taking a fixed driving-field strengthλ=6Γ(the open circles),in exact agreement with the numerical results for=0(the red solid line),and 1(the dashed line).

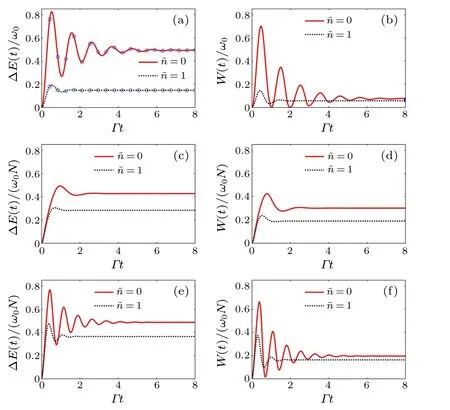
Fig.1.(a)–(d)Time evolution of the increased energy ?E/(ω0N)and the ergotropy W for N = 1 (top) and N = 10 (middle) with a fixed driving-field strength λ =6Γ.(e)and(f)The dynamics for a relatively larger driving field λ =10Γ and N=10.Different curves correspond to different values ofi.e.,=0(red solid line)and =1(black dashed line).The open circles in (a) represent the analytical result given by Eq.(7).The other parameters are Γ =1 and ω =ω0=1000Γ.

From Fig.1(a),one can see that the increase energy ?E(t)shows damped oscillations and approaches to its associated steady-state value ?E(∞)/ω0= [E(∞)-E(0)]/ω0→-b1,whereE(∞)=ω0a1,as expressed by Eq.(7).Note that ?E(∞)increases monotonically with the increase ofλ.Hereafter,we focus on the steady-state values of the energy and the ergotropy and adopt the short-hand notations ?E=?E(∞)andW=W(∞).

In Fig.1(b),we show the ergotrogyW(t)againsttby taking a fixed driving-field strengthλ=6Γfor=0 (the red solid line),1(the dashed line).Att=0,the initial Gibbs state ?ρ0is indeed the passive state, and therebyW(0)=0.With the time evolution, the role of the driving field results in the damped oscillations ofW(t), which is smaller than ?E(t) at eacht.Ast →∞, one can obtain analytical result of ?ρ(∞),which in turn gives(see Appendix B)

whereχandAhave been defined in Eq.(7)and below.For a fixedλ=6Γ,our numerical results show that the steady state appears at the timeΓt?8, withW/ω0≈0.09 (=0) and 0.063(=1),as shown in Fig.1(b).

Maximizing Eq.(8)with respect toλ,we obtain

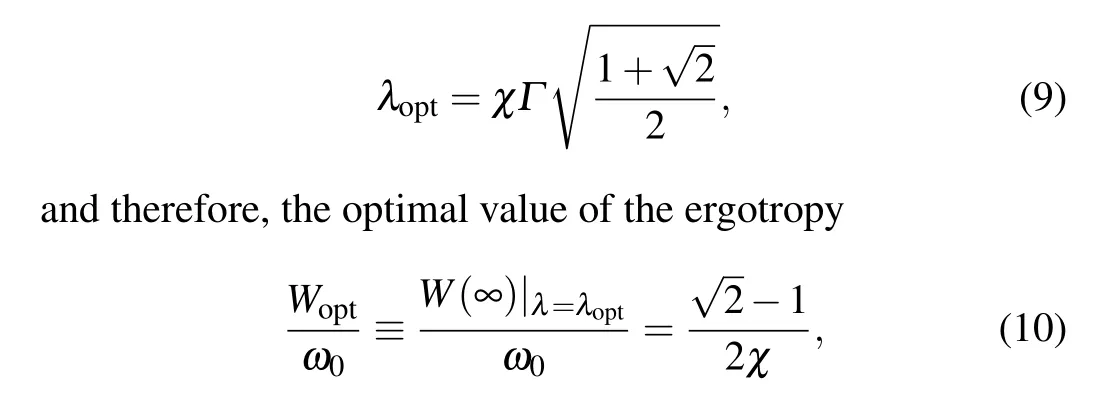
which is independent of the damping rateΓand decreases with the increase ofχ(also).In Fig.2(a), we showW/ω0as a function ofλ/Γfor=0 (the red solid), 1 (the dashed),and 2 (the green dot-dashed).From top to bottom, our numerical results showWopt/ω0≈0.207, 0.069, and 0.041, atλopt/Γ ≈1.099,3.296,and 5.493,respectively,in good agreement with our analytic results(open circles).

4.Quantum advantage of a collective charging protocol

For the finite-Ncase,we consider the collective charging protocol,where dynamics of the QBs is given by the Lindblad master equation(see Appendix A)

The permutation symmetry of the atoms leads to a reduction of the dimension of Hilbert space from 2NtoN+1,where the QB state ?ρis a mixture of the Dicke states{|j,m〉}.For the atoms initially prepared in the Gibbs thermal state,the internal energy is described by Eq.(3).AsN →∞, the mean energy per atom becomesE(0)/(ω0N)→-1/2,similar to Ref.[29].In Figs.1(c)and(d),we takeN=10 and show the time evolution of ?E(t)/(ω0N)andW(t)/(ω0N).Both of them increase to their associated steady-state values asΓt?4,more quickly than that of the single-atom case.However, it is also necessary to show how the observable damps to the steady state for a large value of driving filed strength.In Figs.1(e) and (f),we show the dynamics for a relatively larger driving strength(e.g.,λ=10Γ).One can see that the evolution time to the steady state becomes larger (i.e.,Γt?8).To obtain reasonable steady-states solutions for different values of (N,λ/Γ),we adopt the steady-state solver of the QuTip,which has been widely used in the field of quantum optics.[31]

Fig.2.The ergotropy per atom,W/(ω0N),for different atom numbers N=1(a),N=10(b),and driving-field strength λ =4Γ (c),λ =10Γ(d).(a)The hollow circles given by Eq.(8),the horizontal lines are the upper bound with the conventional charging protocol,which is given by Eq.(10).(c)and(d)The markers are numerical results and the lines are the fitting results.Different colors correspond to different values of i.e.,=0(red),=1(black),and=2(green).Parameters are Γ =1 and ω =ω0=1000Γ.

Fig.3.(a) The maximal ergotropy per atom Wopt/(ω0N), (b) the optimal driving-field strength λopt, (c) the increased energy per atom?E/(ω0N), and (d) the charging efficiency η varies over the number of atoms N.Different colors correspond to different values of =0(red),and =1(black).(b)The green line is the fitting result of =0.(d)The horizontal line indicates η=2-√2.Parameters are Γ =1 and ω =ω0=1000Γ.

5.Conclusion

To summarize, we have investigated the multipartite quantum battery by considering a continuous-wave driving field and a common thermal bath.Different from Changet al.,[29]we adopt the so-called ergotropy to quantify the useful energy stored in the QB.For the single-atom case(i.e.,the conventional charging protocol), we present analytical results of the increased energy and the ergotropy at the long-time limit(i.e., the steady-state ergotropy).By maximizing the steadystate ergotropy,we obtain an optimal value of the driving-field strength,which is dependent on the temperature of the bath(or equivalently,the mean thermal excitation number).Such an observation holds for the finite-Ncase.With a fixed driving strength,we find that there exists the optimal number of atomsNopt,similar to Changet al.[29]This implies that there exists an optimal building block for the multipartite quantum battery.If we adopt the optimal driving field with its strength dependent linearly withN,our numerical results indicate that both the increased energy and the ergotropy increase monotonically withN.Finally, we investigate the ratio of the useful energy and the total increased energy,which also depends on the temperature and the driving field.Using the optimal value of strength for eachN,we find that the ratio also increases monotonically withN.

Appendix A: Lindblad master equation for the system

In the rotating frame with respect toω,the total Hamiltonian is

whereδ=ω0-ω,gj,kis the coupling coefficient between thejth atom and thekth mode of the bath.Considering the resonant case, i.e.,ω=ω0and henceδ=0, the Hamiltonian

which can be rewritten as Eq.(11) in the main text.For the caseN=1,it becomes Eq.(6)in main text.

Appendix B: Analytical results for the singleatom case

For the caseN=1, we first consider a thermal bath, by taking the density matrix ?ρas

where ?Iis the identity matrix and ?σzis the Pauli-zmatrix.Hence,we obtain the ergotropyW,as Eq.(8)in the main text.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.12075209, 11905185, and 11935012)and partially supported by the Science Foundation of Zhejiang Sci-Tech University(Grant No.18062145-Y).