Off-diagonal approach to the exact solution of quantum integrable systems

Yi Qiao(喬藝), Junpeng Cao(曹俊鵬), Wen-Li Yang(楊文力),5,6,?,Kangjie Shi(石康杰), and Yupeng Wang(王玉鵬)

1Institute of Modern Physics,Northwest University,Xi’an 710127,China

2Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

3School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

4Songshan Lake Materials Laboratory,Dongguan 523808,China

5Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China

6Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China

Keywords: quantum spin chain,bethe ansatz,Yang–Baxter equation

1.Introduction

Quantum integrable systems,defined by the Yang–Baxter equation[1,2]or the Lax representation,[3]provide crucial insights in quantum field theory, condensed matter physics and statistical physics.They serve as reliable benchmarks for studying many-body effects, settling debates on fundamental concepts, and exhibiting phenomena such as thermodynamic phase transitions[4]and the generation of fractional charges.[5]These models also have many applications in different fields,such as cold atoms[6–10]and AdS/CFT correspondence.[11,12]

The eigenvalue problem of quantum integrable systems withU(1) symmetry has been tackled by using the methods including coordinate Bethe ansatz,[13]T–Qrelation[14,15]and algebraic Bethe ansatz.[16–20]It should be emphasized that there exist the integrable models which do not possess theU(1) symmetry.Due to theU(1) symmetry broken, it is very hard to construct the suitable reference state.Thus the exact solution of this kind of integrable systems is a challenging issue.Several techniques have been developed to address this problem,including gauge transformation,[21]fusionbasedT–Qrelation,[22,23]q-Onsager algebra,[24,25]separation of variables,[26,27]modified algebraic Bethe ansatz[28,29]and off-diagonal Bethe ansatz.[30,31]The eigenvalues of the transfer matrix of the quantum integrable systems withoutU(1)symmetry are characterized by the inhomogeneousT–Qrelations.However,the associated Bethe ansatz equations(BAEs)are inhomogeneous and the corresponding distributions of Bethe roots are very complicated.Consequently, the thermodynamic Bethe ansatz[32–36]does not work and it is very hard to calculate the exact physical properties in the thermodynamic limit, such as the ground state, elementary excitations and thermodynamic quantities including specific heat and magnetic susceptibility at the finite temperature.

Recently,a novel Bethe ansatz known as thet–Wscheme has been proposed,[37]which effectively tackles the challenges posed by the inhomogeneousT–Qrelations.Taking theXXZspin chain with open boundary condition as an example, we showed the power of this approach with the help of inhomogeneous parameters.[38]The main advantage of this method is that the related BAEs are homogeneous and we can take the thermodynamic limit.We calculated the exact physical quantities such as ground state energy, elementary excitations and surface energy.We also extended the method to the twisted boundary situation.[39]Subsequently,we generalized thet–Wmethod to the finite temperature.The thermodynamic quantities including the free energy of theXXXspin chain with periodic boundary condition were computed.[40]Later,we applied this method to the supersymmetrict–Jmodel,[41]Hubbard model[42]and integrableJ1–J2model with competition interactions,[43,44]among other notable achievements.[45,46]

Thet–Wrelation can be used to determine the energy spectrum directly.Typically,theWoperator can be neglected in the thermodynamic limit, resulting in thet–Wrelation becoming equivalent to the inversion relation,[2,47,48]but the exact proof is absent.Now, we focus on this issue.Our first investigation is as follows.By putting the inhomogeneous parameters into the transfer matrix, we prove that thet–Wrelations are closed at the inhomogeneous points,where the coefficients of theWterms are zero.The inhomogeneous parameters are utilized as the auxiliary functions to determine the distribution of zero roots in the thermodynamic limit.[38]In this paper, we analytically obtain the eigenfunction of theWoperator in the thermodynamic limit at the ground state, and demonstrate that the leading term in thet–Wrelation is quantum determinant instead of theWterm.We take the isotropic spin-1/2 chain as an example.The model Hamiltonian reads

for the open boundary condition (OBC), whereσαnis the Pauli matrix along theα-direction atn-th site,α=(x,y,z),σαN+1=σα1,p,q,ξare the boundary parameters associated with the boundary fields andη=i.

The paper is organized as follows.In Section 2,we introduce theXXXspin chain with periodic boundary condition.We show the integrability,t–Wsolutions and the eigenfunction of the transfer matrix andWoperator at the ground state in the thermodynamic limit.In Section 3,we generalized these results to the open boundary case.Section 4 includes the summary and further discussions.Appendix A gives the detailed derivation of thet–Wrelation and Appendix B shows the Hermitian property of the transfer matrix with PBC.

2.Closed chain

2.1.Integrability

Throughout this paper,Vdenotes a two-dimensional linear space and{|m〉,m=0,1}are its orthogonal bases.We shall adopt the standard notations.For any matrixA ∈End(V),Ajis an embedding operator in the tensor spaceV ?V ?···,which acts asAon thej-th space and as identity on the other factor spaces.For the matrixB ∈End(V ?V),Bi,jis an embedding operator ofBin the tensor space,which acts as identity on the factor spaces except for thei-th andj-th ones.

Let us introduce theR-matrixR0,j(u)∈End(V0?Vj),

whereuis the spectral parameter andηis the crossing parameter.TheR-matrix(3)has the following properties:

where tr0denotes trace over the auxiliary spaceV0.The transfer matrixt(u) is the generating function of conserved quantities in the system, and the Hamiltonian (1) is generated byt(u)as

The transfer matrices with different spectral parameters commute mutually,i.e.,[t(u),t(v)]=0,which ensures the integrability of the model(1).

2.2.The t–W scheme

By using the fusion technique,[49,50]we consider the product of transfer matricest(u)andt(u-η)

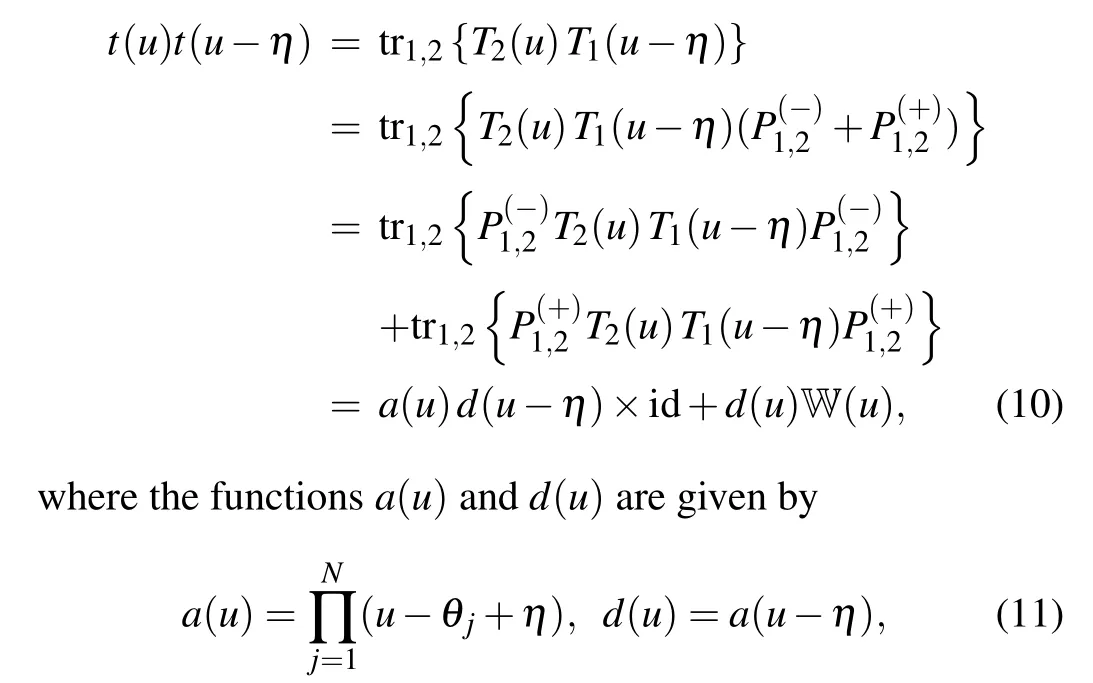
a(u)d(u-η) is the quantum determinant and W(u) is a new operator.The detailed proof is given in Appendix A.At the points of{u=θj},the operator relation(10)can be simplified as

2.3.Exact solution

In order to obtain the exact solution of the spin-1/2XXXclosed chain described by the Hamiltonian(1),let us take the homogeneous limit, i.e.,{θj=0}.Usually, the eigenvaluesΛ(u) andW(u) are expressed by theT–Qrelations with the help of Bethe roots.Here, we quantifyΛ(u) andW(u) by their zero roots as

For the finite system sizeN,one can solve the BAEs(20)and(21)numerically.Substituting the values of roots into Eq.(23),one obtains the energy of the system.The most interesting thing is the thermodynamic limit whereNtends to infinity,which will be addressed in the next subsection.

2.4.Ground state eigenfunctions in the thermodynamic limit

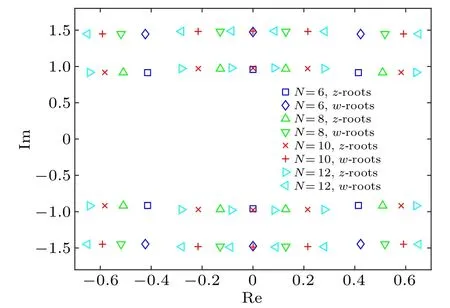
Fig.1.Patterns of zero roots at the ground state with N=6,8,10,12.The data are obtained by using the exact numerical diagonalization with the inhomogeneous parameters{θj =0}.

The role of inset inhomogeneous parameters is to help us to determine the density ofz-roots.Take the difference of Eq.(15) at two nearest inhomogeneous points.In the thermodynamic limit, we set that the density of inhomogeneous parameters as theδ-function.Then we have

3.Open chain

3.1.Integrability

Next, we consider the open boundary condition.The boundary reflections are characterized by the reflection matrices

Due to the boundary reflection, we should introduce the reflecting monodromy matrix

3.2.The t–W scheme

Following the idea of fusion, we still consider the product of two transfer matrices with certain shift of the spectral parameter

whereρ2(u)=-u(u+2η).

The first term of Eq.(60) give a number which is the quantum determinant

where

The fusion does not break the integrability of the system,thus the transfer matrix and the fused transfer matrix commutate with each other.Thus they have common eigenstates.Acting the operator relation(71)on a common eigenstate,we obtain thet–Wrelation

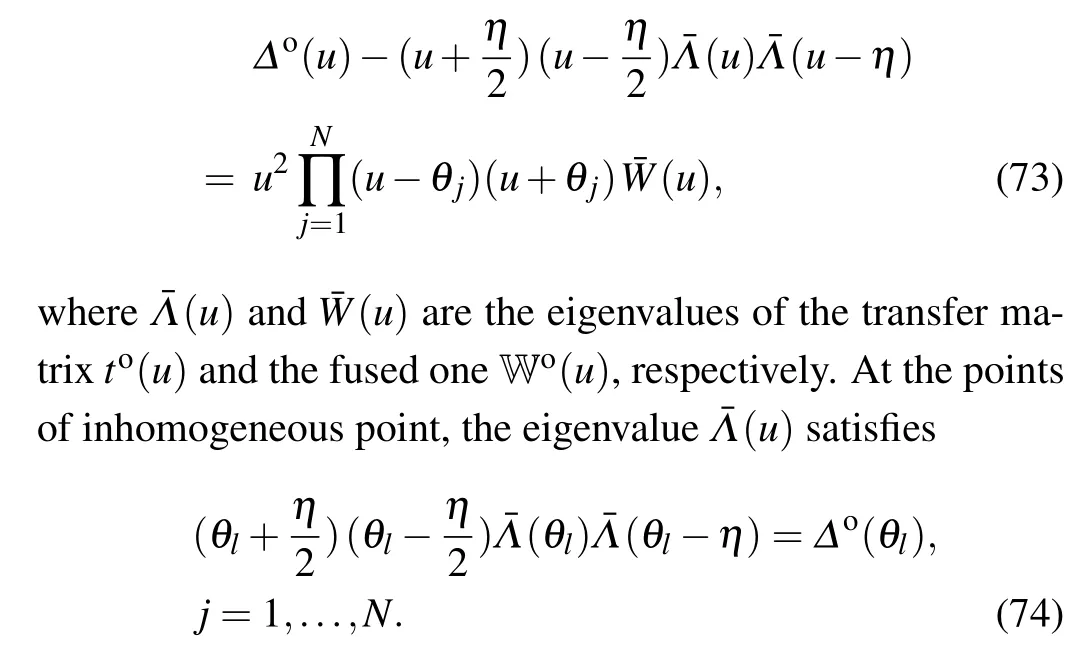
3.3.Exact solution

The exact solution of the system does not depend on the inhomogeneous parameters.Thus we set them as zero.From the definitions, we know that the eigenvalue function(u)is a polynomial ofuwith degree 2N+2 and also satisfies the crossing symmetry and asymptotic behavior

Combining the expansions (77) and (78), thet–Wrelation(73)and the Hermitian relation(85), we conclude that ifzjis a root of(u),thenz*jmust be the root and that ifwjis a root of(u),thenw*jmust be the root.

3.4.Eigenfunctions in the thermodynamic limit at the ground state

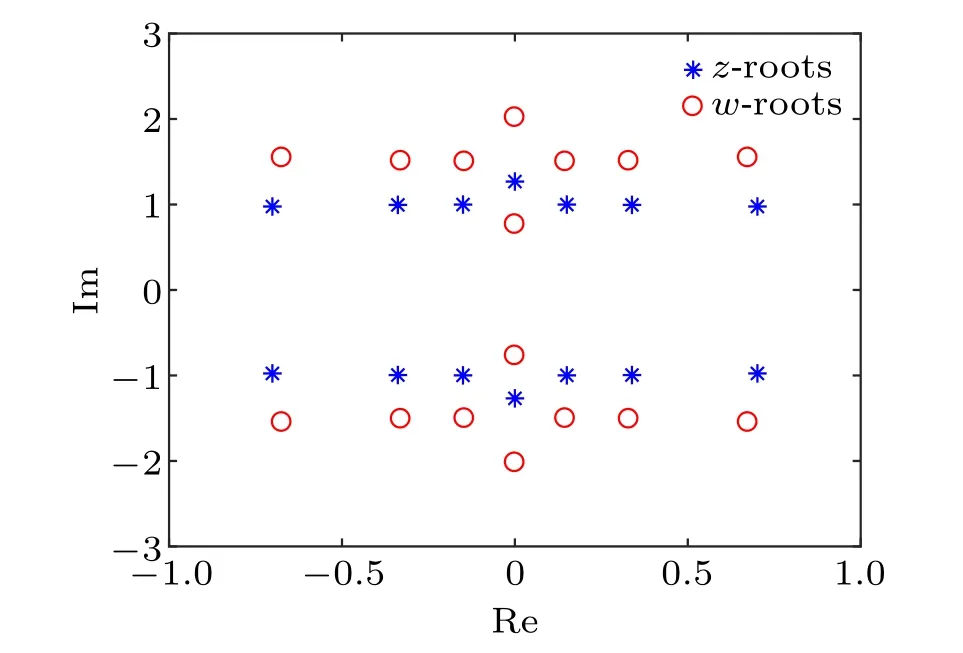
Now, we consider the leading terms of(u) in the thermodynamic limit.Analogous to the case of the periodic boundary condition, we set the variablezj=u(2)j+ηin BAEs(79)and multiply it by its conjugate counterpart.As a result,we obtain

By taking the derivative of the logarithm of Eq.(98),we obtain

Substituting Eq.(87)into Eq.(99),we have

Substituting Eq.(90) into Eq.(100) and solving it by the Fourier transformation, we obtain the densities ofw-roots at the ground state

4.Conclusion

In this paper,we take theXXXspin chain as an example to study thet–Wscheme for the quantum integrable systems.We present the exact solutions of the model with periodic and generic open boundary conditions.We also obtain the analytical expressions of the ground state eigenfunctions of the transfer matrix and W operator in the thermodynamic limit.By analyzing these expressions,we find that the ratio of the quantum determinant with theWfunction converges to zero when the number of size tends to infinity.Thus the main contribution in thet–Wrelation comes from the quantum determinant.This finding serves as a compelling proof of the validity of the extensively applied inversion relation in the field of integrability.

Appendix A:Proof of thet–Wrelation

Starting from the YBE (6) with certain shift of spectral parameter and using the fusion technique,[49,50]we obtain

From the constructions(A4)and(A6),we know that the W(u)operator is an operator polynomial ofuwith the degreeN.

Appendix B:Hermitian property of the transfer matrix

Combining the relations(B4)and(14)–(19),we conclude that ifzjis the solution ofΛ(u), its complex conjugationz*jmust be the solution,and ifwjis a solution ofW(u),thew*jmust be the solution.

Acknowledgments

Project supported by the National Key R&D Program of China (Grant No.2021YFA1402104), the National Natural Science Foundation of China (Grant Nos.12247103,12305005, 12074410, 11934015, and 11975183), Major Basic Research Program of Natural Science of Shaanxi Province (Grant Nos.2021JCW-19 and 2017ZDJC-32),Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No.XDB33000000), Young Talent Fund of Xi’an Association for Science and Technology(Grant No.959202313086), and Shaanxi Fundamental Science Research Project for Mathematics and Physics (Grant No.22JSZ005).