麥克斯韋滾擺的力學過程分析

李鐵平,萬 淼,金三梅,景銳平

(中國地質大學(武漢) 數學與物理學院,湖北 武漢 430074)

麥克斯韋滾擺如圖1所示,當轉動滾擺的軸,使滾擺上升到頂點時,滾擺儲蓄一定的勢能. 當滾擺被松開,開始旋轉下降,滾擺勢能逐漸減小,動能(平動動能和轉動動能)逐漸增加. 當懸線完全松開,滾擺不再下降時,轉動角速度與下降平動速度達到最大值,動能最大. 由于滾擺仍繼續旋轉,它又開始纏繞懸線使滾擺上升. 在滾擺上升的過程中動能逐漸減小,勢能逐漸增加,上升到原來高度時,動能為零,勢能最大. 如果忽略能量損耗,滾擺每次上升的高度都相同,說明滾擺的勢能和動能在相互轉化過程中,機械能的總量保持不變[1-3]. 玩具溜溜球[4-5]就是麥克斯韋滾擺的普及版.

圖1 麥克斯韋滾擺

1 下降過程的力學分析

重力作用下滾擺的運動是滾擺質心的平動與滾擺繞質心轉動的合運動. 如果不計空氣阻力,滾擺在運動過程中機械能守恒. 在任意時刻,滾擺的總動能E等于質心的平動動能和繞質心轉動的動能之和,即

(1)

式中,J是滾擺對質心軸的轉動慣量.

滾擺的受力情況如圖2所示,圖中r是軸的半徑,T是繩對滾擺的拉力,mg是滾擺受到的重力,由質心運動定理和轉動定律可得[6-7]

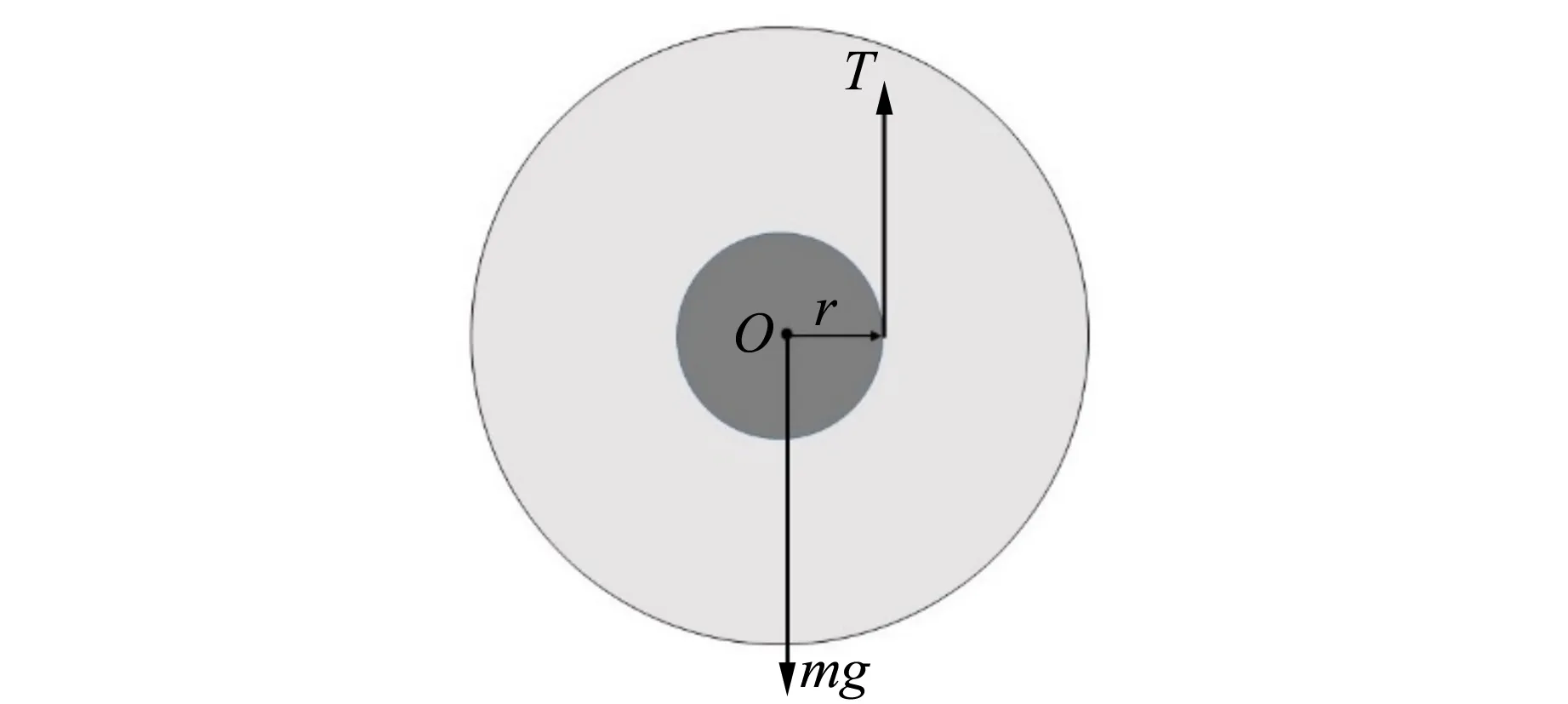
圖2 麥克斯韋滾擺的受力分析

(2)

式中,ac為質心的加速度,β為繞質心轉動的角加速度.由此可解出

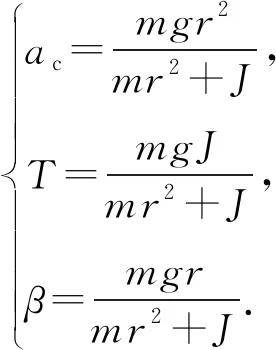
(3)

若滾擺從靜止開始下降,經過時間t,其下降的高度為

(4)

質心的平動動能為

(5)

繞質心的轉動動能為

(6)

顯然滿足

Ekt+Ekv=mgh.

(7)

式(7)表明,滾擺在下降過程中,減少的重力勢能轉化為質心的平動動能與繞質心的轉動動能之和,即滾擺在運動中機械能守恒.

由于轉軸的半徑r遠小于擺輪的半徑R,且擺輪的質量主要分布于擺輪的邊緣,所以有J?mr2,從而有Ekt?Ekv,即滾擺質心的平動動能很小,而滾擺質心速度與擺輪邊緣轉動線速度的比值為

(8)

所以視覺上的感受是轉軸平移很慢,而擺輪轉得很快.

當滾擺下降到最低點時,擺輪的轉動動能達到最大值,由于轉動的慣性,滾擺開始反向纏繞懸線,下落過程中獲取的平動動能和轉動動能將重新轉化為重力勢能,輪的轉速逐漸減小,質心位置升高,重力勢能增大.即到最低點后,滾擺的動能轉換為重力勢能,直至到達最高位置.然后滾擺在重力作用下再次下降,如此反復……

2 回轉點的力學分析

若要優化麥克斯韋滾擺結構,可減少平動動能在動能里面的占比,讓勢能盡可能多地變成轉動動能.

滾擺下落到最低點時,質心速度反向是否會損失部分能量?如圖3所示,質心速度的反轉不是“瞬時”完成,而是經歷向下的質心速度,改變成水平速度,再轉化向上的速度,其中能量依然保持守恒.

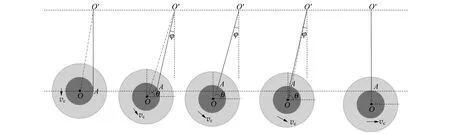
(a) (b) (c) (d) (e)

分析質心速度的改變過程,必然需要考慮質心速度水平方向改變的動力來源.

圖3中的(a)～(e)為滾擺在最低點的運動過程. 在該過程中,系統的質心位置下降,重力勢能減小,動能增加. 其中,圖3(a)是滾擺質心達到懸線末端時的狀態圖,滾擺在下落接近最低點時,滾輪懸掛點A離開鉛直位置,懸線略為傾斜,由于擺繩在內輪的切線方向,故切點A的速度可表示為vA=vc-ωr.剛開始點A在OO′連線右下方,OO′是頂端懸掛點O′與滾擺中心O的連線,如圖3(b)所示,此時拉力矩方向與滾輪角加速度β方向相同,轉動加速.由于滾輪受到的合力導致滾輪做回復到鉛直位置的運動,因此質心水平方向的速度增加,豎直方向速度減小,即vc方向偏離鉛直位置. 隨著滾輪的轉動,某一時刻點A會落在OO′的連線上,如圖3(c)所示,此時系統所受的拉力矩減小到0,轉速達到最大. 滾輪繼續運動,某一時刻點A會落在OO′的連線左上方,如圖3(d)所示,此時拉力矩方向與滾輪角加速度β方向相反,轉動動能減小,平動動能增加,即轉動減速,平動加速. 由于點A受到向右的分力作用,直到點A回復到鉛直位置,如圖3(e)所示,此時小球中心O到達最低點,滾輪回復到鉛直位置,質心速度變為水平速度.

懸線拉力將原先質心向下的速度改變方向,直到最低點速度為水平方向,其平動動能和轉動動能到達最大值,理論上沒有發生能量的損耗;如果忽略懸線的微小偏移,無法理解質心平移速度的反轉.

其后發生的上升過程與降落過程正好相反,就不再討論了.

通過力學模擬與簡化分析,可以得到懸繩最大拉力

(9)

代入實際麥克斯韋滾擺的參考值,J=20mr2,h=1 m,r=0.5 cm,得到Tmax≈20mg.最大拉力確實遠遠大于滾擺的重力mg,所以很多研究者略去力學過程的分析,只是簡單的把最低點的回轉過程理解為沖擊模式.

在滾擺整個運動過程中,滾擺在理論上是能回復到釋放點的.但本文的模型是基于忽略空氣阻力、輕質彈性細線,也沒有考慮轉軸系繩點在技術上會發生移動摩擦.通過適當處理,系繩點的移動可能減少到極值;但空氣阻力無法克服,會導致部分能量損耗,還有非絕對剛性的細繩也會導致部分能量損耗;另外細繩質量也會導致一定的能量消耗.

3 結束語

滾擺物理裝置具備極高的保守能量轉化率,對其運動轉向的分析大多采用“沖擊”模式,夸大了繩索非彈性形變帶來的能量損失.實際生活中,通過對滾擺適當改進就可讓其32次的上下往返.