基于HVSR和VRSR法的場地地震響應分析
李孝波, 宋霖君, 宣雨童, 吳義文, 歐陽剛壘
(1. 防災科技學院 地質工程學院,河北 三河 065201; 2. 河北省地震災害防御與風險評價重點實驗室,河北 三河 065201)
場地地震響應是地震工程領域重要的研究課題之一,不同場地的地震響應各不相同[1-2]。基于觀測數據的場地地震響應分析方法,依據是否使用參考場地常分為參考場地法和非參考場地法[3]。參考場地方法(reference site method,RSM,又稱傳統譜比法)最早由Borcherdt[4]提出,該法在場地反應分析中運用廣泛,使用時須先選取一個參考場地(基巖場地),然后再用研究場地與參考場地的傅氏譜比估計場地反應,應用該方法的關鍵在于參考場地的選擇,若參考場地的反應可以忽略,則用該法估計的場地反應是可靠的。Andrews[5]在傳統譜比法的基礎上擴展延伸出了線性反演法,該方法基于廣義反演技術(generalized inversion technique,GIT)能從多次地震、多個場地的強震記錄中反演估計震源效應、路徑效應和每個場地的場地反應。參考場地方法物理涵義明確,但在實際應用過程中通常很難找到合適的參考場地,于是學者們又對非參考場地方法可行性進行了摸索研究。
非參考場地方法中最常用的是水平與豎向譜比(horizontal-to-vertical spectral ratio,HVSR)法[6]。與傳統譜比法、廣義反演法相比,水平與豎向譜比法不受參考場地、參考事件的約束,利用單臺觀測數據即可獲得較為合理的場地卓越頻率。依據觀測數據的來源,HVSR法又可分為地脈動水平與豎向譜比(horizontal-to-vertical spectral ratio of microtremors,MHVR)法[7-9]和強震動水平與豎向譜比(horizontal-to-vertical spectral ratio of earthquake motions,EHVR)法[10-12],兩種方法都得到了較好的應用。例如,Wen等[13]通過MHVR曲線較好地評價了不同場地類別土層的地震響應;Kawase等[14]在通過進行強震動與地脈動比值(earthquake to microtremor ratio,EMR)和豎向與豎向譜比值(vertical to vertical spectral ratios,VVR)的雙重修正,拓寬了HVSR方法的應用范圍,提高了獲得場地卓越頻率的準確性;宗建業等[15]基于在廣州地區獲取的背景噪聲,采用HVSR法得到了場地共振頻率和放大系數的分布結果,并利用共振頻率與沉積厚度的轉換關系探討了廣州地區沉積層厚度的變化規律;師黎靜等[16]通過對不同類別場地上的MHVR曲線分析,得出地脈動卓越周期劃分方案。胡鵬等[17]基于四川石棉縣測得的60余次地脈動數據,通過MHVR曲線估算場地覆蓋土層厚度,從而揭示該研究區隱伏斷層多表現為卓越頻率高且放大倍數較低等規律。總體而言,即使在復雜的地質條件下,MHVR曲線給出的場地卓越頻率和放大系數都體現出了較好的相關性[18]。
此外,在EHVR法的應用方面,Kawase等[19]利用仙臺MHVR與EHVR曲線進行對比驗證,發現兩者在低頻區段具有良好的相似性;Harsuko等[20]通過EHVR曲線獲取龍目島強震臺站場地放大倍數;朱榮歡等[21]基于EHVR曲線對云南區域地震臺網臺站的場地響應進行研究,得出各強震臺站場地地震響應在低頻段相對穩定,高頻段則存在部分放大的現象;陳永新等[22]基于日本強震動觀測臺網中數百條強震動記錄,通過EHVR曲線對比三種不同獲取場地卓越頻率的方法,認為地表/地下傅里葉譜譜比法能獲取較為準確的卓越頻率;姜秀璇等[23]基于祁連山主動源觀測臺網中40個短周期觀測臺數據,利用EHVR曲線得到大部分臺站在各頻段都有明顯的放大(衰減)作用;師黎靜等[24]對比戈壁砂礫地區EHVR和MHVR譜比曲線,發現兩種方法得到的卓越頻率具有很高的一致性。
值得注意的是,EHVR和MHVR曲線都是基于傅里葉譜譜比得出的,且EHVR曲線還常會存在毛刺太多、不能清晰識別出場地卓越頻率與放大系數的問題[25-26]。Yamazaki等[27]提出直接用5 %阻尼比的速度反應譜來代替平滑后的傅里葉譜,即速度反應譜譜比(velocity response spectrum spectral ratio,VRSR)法。Zhao等[28]利用VRSR方法對日本強震臺站的場地類別進行了判別;Pinzón等[29]基于西班牙強震記錄,通過VRSR法獲得了場地較為真實的卓越頻率,且消除了方向性效應中的不確定性影響;羅桂純等[30]基于理縣木卡臺獲取的地震記錄,采用 VRSR法探究了場地反應的非線性特征,認為VRSR曲線平滑、峰值突出,能清楚地給出場地的卓越頻率。綜上所述,相較于EHVR曲線,VRSR曲線即不會出現“過平滑”的現象,又可以避免曲線平滑和截取S波過程中引入的誤差,使得卓越頻率的識別更加清晰方便。
然而,無論是地脈動數據還是強震動數據,采用不同方法開展同一場地地震響應特征對比研究的成果仍然不多。因此,為進一步探究不同方法在同一場地地震響應特征分析的異同,本文基于2018年松原5.7級地震的強震動記錄,結合在強震臺站獲取的地脈動數據,采用水平與豎向譜比法和速度反應譜譜比法,探究達里巴、東三家子、風華以及寶甸等4個強震臺站場地的地震響應特征,以期為依托強震記錄和地脈動數據開展場地地震響應分析提供參考。
1 數 據
1.1 強震動
2018年5月28日,吉林松原市寧江區(北緯45.27°,東經124.71°)發生5.7級地震,震源深度13 km,這是繼2013年吉林松原5.8級之后,吉林省發生的又一次社會影響較大、受災比較嚴重的破壞性地震[31]。地震共觸發強震臺站11個(如圖1所示),其中位于松原市境內的有4個,分別為達里巴臺(22DLB)、風華臺(22FHT)、寶甸臺(22BDT)以及東三家子臺(22DSJ)。從表1可以看出,4個強震臺站的震中距位于15.5 ~ 112.5 km,場地類型均為土層,無基巖臺站。4個臺站的PGA值整體具有隨震中距增加而逐漸減小的趨勢,風華臺的PGA值最大,達到了189.30 gal(NS向)。各強震臺的地震加速度時程曲線如圖2所示。

圖1 強震臺站和地脈動測點的位置Fig.1 The location of strong earthquake station and microtremors measuring point

圖2 地震加速度時程曲線Fig.2 Earthquake acceleration time history curves
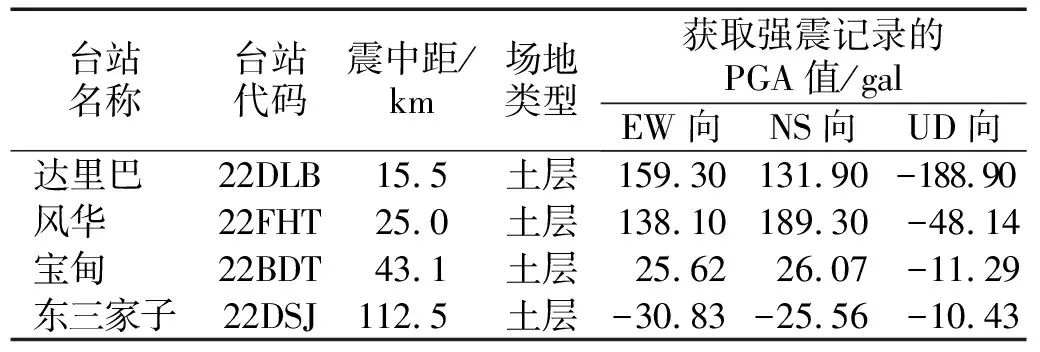
表1 強震臺站參數列表Tab.1 Strong earthquake station parameter list
1.2 地脈動
為了獲取強震臺站所在場地的地脈動數據,依據GB/T 50269—2015《地基動力特性測試規范》[32]中的測試要求,于2019年10月在達里巴、東三家子、風華、寶甸等4個強震臺站附近開展了地脈動測試工作(如圖3(a)、圖3(b)所示),測點的具體位置見圖1。

圖3 地脈動現場測試Fig.3 Field test of microtremor
地脈動測試采用美國Kinematrics公司生產的Basalt數字式記錄儀(如圖4(a)所示)(具體參數詳見https://kinemetrics.com/)和中國地震局工程力學研究所生產的SLJ-100型加速度計(如圖4(b)所示),同時獲取3個方向的地脈動數據,采樣頻率200 Hz,采樣時間1 800 s。圖5給出了各測點30~90 s的地脈動記錄。

圖4 地脈動測試儀器Fig.4 Microtremor measuring instruments
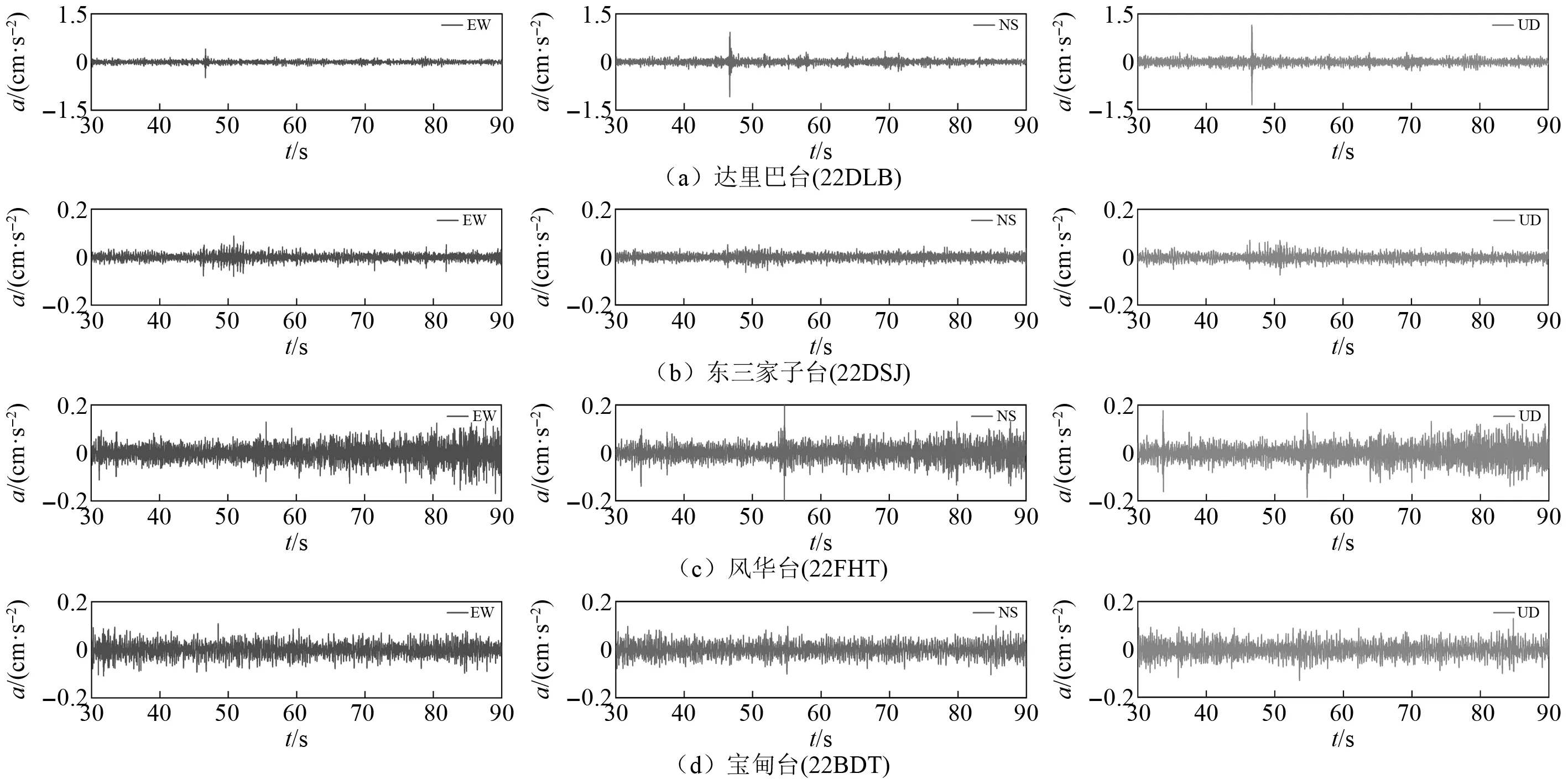
圖5 地脈動時程曲線Fig.5 Microtremor time history curves
2 方 法
2.1 水平與豎向譜比法
Kanai等[33]最早將地脈動用于估計場地地震效應研究, Nakamura[6]提出HVSR法則更加廣泛應用于場地地震反應分析領域。若用H(f)表示地脈動記錄的水平分量,V(f)表示地脈動記錄的豎向分量,則HVSR的計算公式可表示為
(1)
HVSR法的提出主要基于兩個假定[34],即:①水平分量被放大的同時,豎向分量基本不放大,認為豎向傳遞函數為1;②基巖處的HVSR值為1。一般認為,HVSR法可以得到較為可靠的場地卓越頻率,但對場地放大效應有所低估[35-36]。
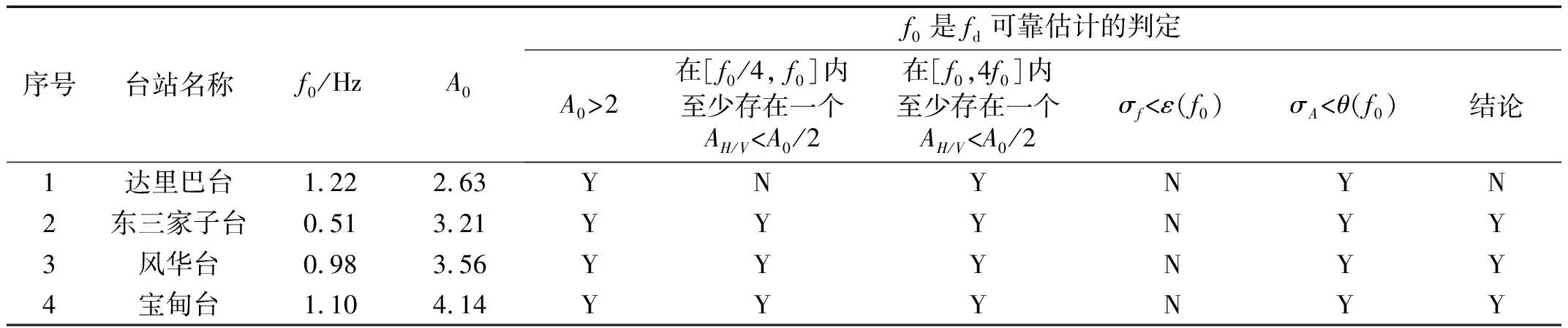
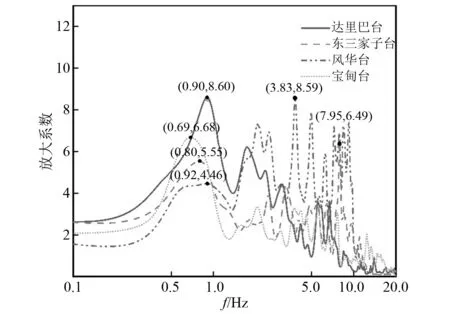
HVSR曲線的形狀與場地條件相關,常有單峰、雙峰以及多峰等多種形式。不同形式的HVSR曲線,擁有不同的峰值頻率f0和放大系數A0。各測點峰值頻率f0能否作為該點土層的卓越頻率fd,常需進行以下5個條件的驗證[37]:①A0>2;②在[f0/4,f0]頻率范圍內,至少存在一個HVSR值(AH/V) 表2 閾值θ(f0)與ε(f0)的取值范圍Tab.2 Threshold rang of θ(f0) and ε(f0) 針對地脈動數據,采用開源軟件Geopsy(https://www.geopsy.org)對其進行處理,主要包括數據選取、帶通濾波、傅里葉譜計算、平滑處理和HVSR值計算等5個步驟。 步驟1數據選取:設定數據窗時長20 s,同時截取UD,NS和EW 3個方向的地脈動數據,為保證數據窗內信號平穩,每個時窗內3個方向的數據均需滿足0.5 步驟2帶通濾波:為保證分析結果的可靠性,選用4階Butterworth帶通濾波函數對每個數據時窗內的原始地脈動數據進行濾波處理,濾波帶寬0.05~20.00 Hz,濾波后的數據再次進行0.5 步驟3傅里葉譜計算:對每個數據時窗內的數據進行快速傅里葉變換(fast Fourier transform,FFT),得出UD,NS和EW 3個方向的傅里葉譜值,完成地脈動數據從時域到頻域的轉換。 步驟4平滑處理:采用Konno-Ohmachi函數[38],對每個傅里葉譜窗內的數據進行平滑處理,平滑帶寬b取為40。 步驟5HVSR值計算:基于HVSR法分別計算每個傅里葉譜窗的HVSR值,得出HVSR曲線,其中水平方向(H向)的數值取NS,EW向的均方根值,每個測點的HVSR曲線取各傅里葉譜窗HVSR曲線的平均值。 強震動數據的處理與地脈動類似,首先采用Seismosignal進行基線校正,并采用4階Butterworth濾波器進行帶通濾波(頻帶范圍0.1~20.00 Hz),然后通過快速傅里葉變換計算傅里葉幅值譜,經Parzen窗(帶寬0.4 Hz)平滑后,最后再給出各測點的HVSR曲線。 反應譜是地震動加速度時間過程作用于單自由彈性體系的最大反應隨體系自振特性(周期、阻尼比)變化的函數關系曲線,常有絕對加速度反應譜、相對速度反應譜、相對位移反應譜[39]。其中,速度反應譜揭示了地震動作用下結構振動能量隨自振頻率的變化規律[40-41]。 VRSR的計算主要包括基線校正、帶通濾波、速度反應譜計算、VRSR值計算等4個步驟。 步驟1基線校正:采用Seismosignal 軟件(v2022)對UD,NS和EW 3個方向的強震數據分別進行基線校正。 步驟2帶通濾波:為保證分析結果的可靠性,選用4階Butterworth帶通濾波函數對強震動數據進行濾波處理,濾波帶寬0.05~20.00 Hz。 步驟3速度反應譜計算:濾波處理完成后,計算每條數據的速度反應譜,得出UD,NS和EW 3個方向的速度反應譜值,阻尼比取為5%。 步驟4VRSR值計算:基于VRSR方法,分別計算每個強震臺站的速度反應譜譜比值,得出VRSR曲線,其中水平方向(H向)數值的計算與HVSR方法一致,即取NS,EW向的均方根值。 圖6給出了4個強震臺站場地的MHVR曲線。從圖6中可以看出,風華臺的MHVR曲線為單峰型,寶甸臺為雙峰型,達里巴臺、東三家子臺則呈現為多峰型。在0.1~20 Hz的頻率范圍內,4個測點的峰值頻帶突出,且都具有中低頻段波動明顯、高頻段相對平穩的變化規律,較好地呈現了地脈動中低頻成分豐富的特點。表3統計給出了各測點的峰值頻率,除東三家子臺處的峰值頻率較低外,其余3個測點的峰值頻率都在1 Hz左右,集中在中頻段(0.98~1.22 Hz)。依據SESAME使用指南判定測點處土層卓越頻率的結果表明,寶甸臺、東三家子臺以及風華臺的峰值頻率可作為該處土層卓越頻率的可靠估計,即寶甸臺、東三家子臺以及風華臺的土層卓越頻率分別為1.10 Hz,0.51 Hz以及0.98 Hz。達里巴臺由于低頻段與中頻段的放大系數相差不大,不滿足在[f0/4,f0]頻率范圍內至少存在一個HVSR值(AH/V) 圖6 MHVR曲線Fig.6 MHVR curves 表3 各測點MHVR曲線的峰值頻率f0、峰值放大系數A0以及地層卓越頻率fd的可靠估計 圖7為4個強震臺站場地的EHVR曲線。從曲線形態上看,寶甸臺的EHVR曲線為單峰型,達里巴臺、東三家子臺以及風華臺則為多峰型。在0.1~20 Hz的頻率范圍內,4個測點的EHVR曲線都展現出了低頻段非常平穩、中高頻段波動明顯的變化特征,體現了強震記錄中高頻成分豐富的特點。基于EHVR曲線的變化規律,易得達里巴臺、寶甸臺的峰值頻率為0.90 Hz和0.69 Hz,均在第一峰值點處取得;東三家子臺、風華臺由于高頻放大效應顯著,峰值頻率為高頻段的7.95 Hz和3.83 Hz,第一峰值點對應的頻率則為0.80 Hz和0.92 Hz,同樣集中于中頻段。放大系數方面,4個測點的放大效應都十分突出,達里巴臺、東三家子臺、風華臺以及寶甸臺與峰值頻率對應的放大系數達到了8.60,6.49,8.59以及6.68,東三家子臺、風華臺與第一峰值點對應的放大系數也達到了5.55和4.46,都較MHVR的放大系數有了較大幅度的提高,體現了地脈動與強震記錄之間震動強度的差異[42]。 圖7 EHVR曲線Fig.7 EHVR curves 圖8為4個測點的VRSR曲線,在0.1~20 Hz的頻率范圍內均呈現出了較為明顯的波動變化,為典型的多峰型曲線。與MHVR曲線相比,VRSR曲線的高頻成分更加豐富,低頻段放大系數具有較大幅度的增加;與此相反,與EHVR曲線相比則是低頻成分更加豐富,高頻段放大系數有一定程度的增大。基于VRSR曲線的變化特征,達里巴臺、東三家子臺、風華臺以及寶甸臺在0.1~20 Hz頻率范圍內的峰值頻率分別為1.48 Hz,0.89 Hz,2.05 Hz和0.66 Hz,對應的放大系數為4.58,8.19,10.90和7.96,同樣體現出了顯著的地震動放大效應。 圖8 VRSR曲線Fig.8 VRSR curves 綜上所述,4個測點MHVR,EHVR和VRSR曲線的變化趨勢各不相同,雖然都體現出了較為顯著的放大效應,但MHVR曲線中低頻段變化明顯,EHVR曲線中高頻段波動突出,VRSR曲線則全頻帶(0.1~20 Hz)都變化頻繁。究其原因,除與HVSR,VRSR法的計算原理相關以外,地脈動與強震動記錄在振動強度、頻譜特性等方面的差異也是一個不可忽略的因素。 圖9給出了每一個測點的MHVR,EHVR和VRSR曲線。整體上看,即使在同一場地條件下,MHVR,EHVR和VRSR曲線的變化規律也差異明顯。其中,MHVR曲線在0.1~20 Hz頻率范圍內的變化最為平穩,峰值頻率容易識別,但放大系數較小,對場地地震響應有所低估;除達里巴臺外,東三家子臺、風華臺以及寶甸臺的EHVR和VRSR曲線在中高頻段都具有大體一致的變化趨勢,峰值頻率較易識別,但VRSR曲線的放大系數整體偏大;與此相反,達里巴臺VRSR曲線的放大系數則較EHVR小,中高頻段的波動幅度也偏小,推測與該臺距震中較近(震中距15.5 km),加速度響應較速度更為靈敏有關。 圖9 MHVR,EHVR以及VRSR曲線的對比Fig.9 Comparative Analysis of MHVR, EHVR and VRSR curves 此外,值得注意的是在MHVR曲線的峰值頻段,EHVR和VRSR都表征出了顯著的放大效應,即EHVR和VRSR曲線的一階峰值頻率在MHVR曲線的峰值頻段取得。表4給出了各點的(一階)峰值頻率及其對應的放大系數,囿于基本原理的不同,MHVR,EHVR和VRSR給定的(一階)峰值頻率略有差異,但放大系數(除達里巴臺外)卻具有大致相同的變化規律。達里巴臺、東三家子臺、風華臺以及寶甸臺所處場地的(一階)峰值頻率(放大系數)范圍分別為0.90~1.48 Hz(2.63~8.60),0.51~0.89 Hz(3.21~8.19),0.47~0.98 Hz(3.56~8.41)以及0.66~1.10 Hz(4.14~7.96)。 表4 各測點(一階)峰值頻率及其對應的放大系數Tab.4 The (first order) peak frequency of each measuring point and its corresponding amplification factor 總的來說,本文基于2018年松原5.7級地震的強震動記錄,結合在強震臺站附近獲取的地脈動數據,采用水平與豎向譜比法和速度反應譜譜比法,探究了4個強震臺站場地地震響應特征,獲得了一些有益的結論。然而,針對場地地層結構對地震響應的影響,VRSR曲線峰值頻率的快速識別以及EHVR和VRSR反應的地震動高頻特征等問題仍值得開展進一步的深入探究。 致謝 本文強震動數據由中國地震局工程力學研究所國家強震動觀測中心提供,在此表示感謝。
2.2 速度反應譜譜比法
3 結 果
3.1 MHVR和EHVR

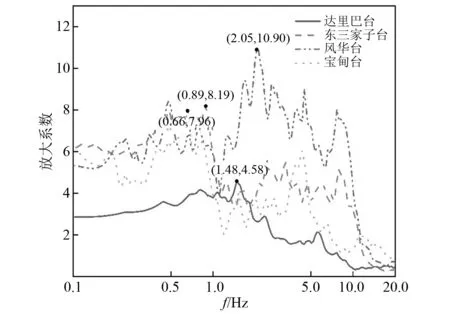
3.2 VRSR
4 結 論



