考慮材料性能不確定性的聲振強(qiáng)耦合系統(tǒng)穩(wěn)健拓?fù)鋬?yōu)化

鄭文治, 陳海波, 操小龍

(1. 中國科學(xué)技術(shù)大學(xué) 近代力學(xué)系 中國科學(xué)院材料力學(xué)行為與設(shè)計(jì)重點(diǎn)實(shí)驗(yàn)室,合肥 230027;2. 北京機(jī)電工程研究所,北京 100074)

拓?fù)鋬?yōu)化由于其可以相當(dāng)靈活地改變結(jié)構(gòu)的拓?fù)錁?gòu)型,在振動(dòng)與噪聲控制領(lǐng)域受到了廣泛關(guān)注。Du等[1]以輻射聲功率最小為目標(biāo),對平板的材料分布進(jìn)行了拓?fù)鋬?yōu)化設(shè)計(jì);之后Du等[2]將此優(yōu)化框架擴(kuò)展到微結(jié)構(gòu)的拓?fù)鋬?yōu)化設(shè)計(jì);Zhang等[3]以目標(biāo)點(diǎn)的聲壓最小為目標(biāo),基于固體各向同性材料懲罰(solid isotropic material with penalization,SIMP)模型對振動(dòng)結(jié)構(gòu)的阻尼材料分布進(jìn)行了優(yōu)化設(shè)計(jì);吳振云等[4]使用非負(fù)聲強(qiáng)識(shí)別結(jié)構(gòu)表面對遠(yuǎn)場聲輻射起主要貢獻(xiàn)的區(qū)域,對約束阻尼板阻尼材料的最優(yōu)分布進(jìn)行研究。目前,大多數(shù)聲振優(yōu)化的研究僅考慮弱耦合,即僅考慮結(jié)構(gòu)對聲場的作用而忽略了聲場對結(jié)構(gòu)的反作用。對于像空氣這種流體密度遠(yuǎn)低于結(jié)構(gòu)的聲學(xué)介質(zhì)來說,這種簡化通常是合理的,但對于像水這種重流體,則必須考慮結(jié)構(gòu)和聲學(xué)介質(zhì)之間的相互作用,即強(qiáng)耦合作用。已有學(xué)者針對強(qiáng)耦合情況開展了研究工作。Shu等[5]基于水平集方法對聲振耦合系統(tǒng)進(jìn)行了拓?fù)鋬?yōu)化設(shè)計(jì);Chen等[6]以目標(biāo)點(diǎn)的聲壓級(jí)最小為目標(biāo),對聲振耦合系統(tǒng)中的復(fù)合材料板的微結(jié)構(gòu)進(jìn)行了優(yōu)化。上述兩項(xiàng)研究都基于有限元法,針對有限域的內(nèi)聲場問題開展的。對于無限域外聲場問題,有限元法需要對較大的聲場域進(jìn)行離散,計(jì)算效率大大降低,且無限遠(yuǎn)處的無反射條件難以精確滿足,需要進(jìn)行麻煩的特殊處理[7-8]。邊界元法只需在聲場邊界進(jìn)行離散,且自動(dòng)滿足無限遠(yuǎn)處聲場的無反射條件,對于分析外聲場問題有很大的優(yōu)勢,因此基于有限元-邊界元耦合的分析方法可以有效地用于解決外聲場與結(jié)構(gòu)的耦合問題[9-10]。近些年,針對外聲場強(qiáng)耦合問題的拓?fù)鋬?yōu)化的研究工作也已開展起來[11-12]。Zhao等采用有限元-邊界元耦合方法,以輻射聲功率級(jí)最小為目標(biāo),基于材料屬性的有理近似方法(rational approximation of material properties, RAMP)模型和移動(dòng)漸近優(yōu)化算法(method of moving asymptotes,MMA)對聲振耦合系統(tǒng)的材料分布進(jìn)行了拓?fù)鋬?yōu)化設(shè)計(jì)。

上述的拓?fù)鋬?yōu)化都是在確定性的條件下進(jìn)行的。然而在實(shí)際工程中,由于制造、裝配、外部載荷的不可完全預(yù)測等因素,導(dǎo)致材料屬性、幾何尺寸、外部載荷等存在不確定性。傳統(tǒng)的確定性拓?fù)鋬?yōu)化忽略了系統(tǒng)的不確定性,可能導(dǎo)致優(yōu)化的結(jié)果是次優(yōu)的甚至完全不符合實(shí)際。因此,開展考慮不確定性的拓?fù)鋬?yōu)化研究工作是很有必要的。

考慮不確定性因素的拓?fù)鋬?yōu)化通常分為兩種:可靠性拓?fù)鋬?yōu)化[13-14]和穩(wěn)健拓?fù)鋬?yōu)化。可靠性拓?fù)鋬?yōu)化關(guān)注的是在極端條件下系統(tǒng)的工作狀況,而穩(wěn)健拓?fù)鋬?yōu)化側(cè)重于在一定程度上減小目標(biāo)函數(shù)對不確定性參數(shù)的敏感性。趙清海等[15]考慮載荷的不確定性,針對多材料結(jié)構(gòu)進(jìn)行了穩(wěn)健拓?fù)鋬?yōu)化;李冉等[16]基于隨機(jī)有限元方法進(jìn)行不確定性分析,考慮增材制造工藝中引起的表面層厚度不確定性進(jìn)行了穩(wěn)健拓?fù)鋬?yōu)化;Yin等[17]基于隨機(jī)攝動(dòng)方法進(jìn)行不確定性分析,將聲介質(zhì)的物理參數(shù)、外部載荷和材料特性視為隨機(jī)參數(shù),對聲振耦合系統(tǒng)的微結(jié)構(gòu)進(jìn)行了穩(wěn)健拓?fù)鋬?yōu)化設(shè)熟計(jì)。Keshavarzzadeh等[18]基于混沌多項(xiàng)式展開(polynomial chaos expansion,PCE)方法量化不確定性的傳播和響應(yīng)的靈敏度,建立可靠性拓?fù)鋬?yōu)化設(shè)計(jì)方法和穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)方法;Zhang等[19]將PCE方法拓展到聲子晶體的穩(wěn)健拓?fù)鋬?yōu)化中;Torii等[20]使用該方法處理了考慮不確定量的發(fā)熱、不確定位置的發(fā)熱和不確定位置損傷的熱傳導(dǎo)穩(wěn)健拓?fù)鋬?yōu)化;Kang等[21]考慮材料梯度界面梯度的不確定性,基于PCE方法和水平集方法對多材料結(jié)構(gòu)進(jìn)行了穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)。以上研究均未涉及外聲場強(qiáng)耦合聲振系統(tǒng)問題,我們的文獻(xiàn)調(diào)研也未見相關(guān)報(bào)道。

本文針對外聲場與結(jié)構(gòu)強(qiáng)耦合問題,建立了考慮材料性能空間不確定性的穩(wěn)健拓?fù)鋬?yōu)化模型。使用RAMP模型來描述材料分布;假設(shè)材料的彈性模量服從高斯隨機(jī)場分布,通過級(jí)數(shù)最優(yōu)線性估值(expansion optimal linear estimation,EOLE)方法將彈性模量隨機(jī)場離散成有限個(gè)隨機(jī)變量;基于PCE方法進(jìn)行隨機(jī)響應(yīng)預(yù)測和隨機(jī)響應(yīng)的靈敏度分析;采用MMA算法進(jìn)行設(shè)計(jì)更新,最終得到最優(yōu)的材料布局。最后通過數(shù)值算例說明了考慮材料性能不確定性的必要性和本文所建立方法的有效性。

1 有限元-邊界元分析方法

1.1 結(jié)構(gòu)有限元分析

在簡諧激勵(lì)作用下,有限元離散后的結(jié)構(gòu)振動(dòng)方程可表示為

(K-iωC-ω2M)u=Kdu=f

(1)

式中:K,C和M分別為結(jié)構(gòu)剛度矩陣、阻尼矩陣和質(zhì)量矩陣;u為節(jié)點(diǎn)位移;f為等效節(jié)點(diǎn)載荷;ω為激勵(lì)圓頻率。

考慮聲場對結(jié)構(gòu)的反作用時(shí),外載荷表示為

f=fs+fp

(2)

式中:fs為直接加載到結(jié)構(gòu)的載荷;fp為聲場反作用到結(jié)構(gòu)上的載荷。將式(2)代入式(1)可得

Kdu=fs+fp

(3)

采用瑞利阻尼模型,結(jié)構(gòu)的阻尼矩陣可以表示為剛度矩陣和質(zhì)量矩陣的線性組合

C=α0M+β0K

(4)

式中,α0和β0為瑞利阻尼模型的相關(guān)系數(shù)。

1.2 聲學(xué)邊界元分析

在均勻理想流體介質(zhì)中,聲場的控制方程為Helmholtz方程

?2p(x)+k2p(x)=0, ?x∈Ωf

(5)

式中:p為聲壓;k=ω/cf為波數(shù),ω為圓頻率,cf為波速。應(yīng)用格林第二公式,并將源點(diǎn)趨近于邊界,可得常規(guī)邊界積分方程(conventional boundary integral equation, CBIE)

(6)

式中:x為源點(diǎn);y為場點(diǎn);q(y)=?p(y)/?n(y)為通量,n(y)為邊界點(diǎn)y處的外法線方向向量;系數(shù)c(x)的大小由點(diǎn)x處的幾何性質(zhì)決定,當(dāng)點(diǎn)x處為光滑邊界時(shí),c(x)=0.5;對于三維聲學(xué)問題,其基本解為

(7)

式中,r=|x-y|為源點(diǎn)x和場點(diǎn)y的距離。

同時(shí)對式(6)的兩邊對源點(diǎn)x所在邊界外法向方向求導(dǎo),即可得超奇異邊界積分方程(hypersingular boundary integral equation, HBIE)

(8)

對外聲場進(jìn)行分析時(shí),單獨(dú)使用式(6)或式(8)會(huì)引起解的非唯一性問題,因此Burton等[22]提出了將兩式進(jìn)行線性組合,即Burton-Miller方法

CBIE+αHBIE=0

(9)

式中,α為耦合系數(shù),本文取為-i/k[23]。對聲學(xué)邊界進(jìn)行離散,得到式(9)的離散格式

Hp=Gq

(10)

式中:H和G為邊界元系數(shù)矩陣;p和q分別為邊界節(jié)點(diǎn)聲壓及其法向通量。

1.3 有限元與邊界元耦合

結(jié)構(gòu)與聲學(xué)耦合面上需滿足位移連續(xù)與力的平衡條件

q=iωρfvf=ω2ρfS-1Cfsu

(11)

fp=Csfp

(12)

式中:ρf為流體介質(zhì)密度;vf為聲場法向速度,Cfs和Csf為結(jié)構(gòu)與流場之間的耦合矩陣;S為邊界質(zhì)量矩陣。

(13)

(14)

(15)

將式(11)、式(12)分別代入式(10)、式(3)中,得到聲振耦合系統(tǒng)控制方程

(16)

通過求解上述方程,就可以完成對聲振耦合系統(tǒng)的分析。整個(gè)系統(tǒng)對外輻射做功的大小可以通過輻射聲功率表示

(17)

式中:W為輻射聲功率; 上標(biāo)()H為共軛轉(zhuǎn)置; Re()為取實(shí)部。輻射聲功率級(jí)可以表示為

(18)

式中,W0為參考聲功率,本文取W0=2×10-12W。

2 隨機(jī)場模型及隨機(jī)響應(yīng)分析

2.1 隨機(jī)場離散

本文考慮采用高斯隨機(jī)場t(x)描述材料彈性模量的不確定性,其均值為μ(x),其協(xié)方差函數(shù)為

(19)

式中: cov(x1,x2)為隨機(jī)場的協(xié)方差函數(shù);σ為隨機(jī)場的標(biāo)準(zhǔn)差;l為隨機(jī)場的相關(guān)長度; |x1-x2|為點(diǎn)x1和點(diǎn)x2的距離。

首先,將隨機(jī)場域離散為一系列節(jié)點(diǎn)x1,…,xn,則隨機(jī)場的協(xié)方差矩陣為

(20)

基于EOLE方法[24],隨機(jī)場可以表示為

(21)

式中:Cv=[cov(x1,x),cov(x2,x),…,cov(xn,x)]T;λk,ψk分別為協(xié)方差矩陣Cm的特征值和與之對應(yīng)的特征向量;ξ1,ξ2,…,ξk,…,ξn為互不相關(guān)的隨機(jī)變量,其均值和方差滿足

E[ξi]=0, E[ξiξj]=δij

(22)

式中: E[]為期望;δij為Kronecker delta符號(hào)。

為了減小問題的維數(shù),將特征值λk降序排列,對式(21)取前s(s≤n)項(xiàng)進(jìn)行截?cái)?/p>

(23)

隨機(jī)場的截?cái)嗑日`差為

(24)

根據(jù)式(23)就可以實(shí)現(xiàn)對隨機(jī)場的有限離散。

2.2 基于PCE方法的隨機(jī)響應(yīng)分析

對隨機(jī)場離散后,得到一系列互不相關(guān)的隨機(jī)變量ξ=[ξ1,ξ2,…,ξs]T, 聲振耦合系統(tǒng)的隨機(jī)響應(yīng)通過PCE方法進(jìn)行預(yù)估

(25)

式中:Y(ξ)為系統(tǒng)響應(yīng);yi為多項(xiàng)式的系數(shù);φi(ξ)為多項(xiàng)式的正交基函數(shù),正交于隨機(jī)變量ξ的概率密度函數(shù)。對于不同的概率分布,多項(xiàng)式的形式會(huì)有不同,例如當(dāng)隨機(jī)變量ξ服從均勻分布時(shí),φi(ξ)為Legendre多項(xiàng)式; 當(dāng)隨機(jī)變量ξ服從高斯分布時(shí),φi(ξ)為Hermite多項(xiàng)式。正交基函數(shù)φi(ξ)滿足

(26)

對于多維隨機(jī)變量ξ=[ξ1,ξ2,…,ξs]T,多項(xiàng)式函數(shù)φi為

(27)

式中:καj為隨機(jī)變量ξj的αj階多項(xiàng)式;φi的階數(shù)為

(28)

為了在保證計(jì)算精度的前提下,有效降低計(jì)算量,一般將式(25)截?cái)酁橛邢揄?xiàng)

(29)

式中,多項(xiàng)式系數(shù)的項(xiàng)數(shù)N+1取決于隨機(jī)變量的維數(shù)s和PCE的階數(shù)m

(30)

求解混沌多項(xiàng)式展開的關(guān)鍵在于求解其中的系數(shù)yi,利用多項(xiàng)式φi的正交特性可得

(31)

由式(31)可得

(32)

(33)

式中:ρ(ξ)為隨機(jī)變量ξ的概率密度函數(shù);ξ(q),w(q)和nq分別為積分點(diǎn)、權(quán)值和積分點(diǎn)數(shù)目。由于本文采用的是高斯隨機(jī)變量,所以采用Gauss-Hermite數(shù)值積分計(jì)算,由此可求解系數(shù)。

計(jì)算得到式(29)的系數(shù)yi后,響應(yīng)Y(ξ)的均值E[Y(ξ)]和標(biāo)準(zhǔn)差σ[Y(ξ)]可以通過下式獲得

(34)

(35)

3 穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)

3.1 確定性拓?fù)鋬?yōu)化數(shù)學(xué)模型

拓?fù)鋬?yōu)化是通過優(yōu)化材料的空間分布,在滿足約束的前提下最大程度的改善結(jié)構(gòu)性能。聲振耦合系統(tǒng)一般選擇位移幅值、聲壓級(jí)、聲功率級(jí)作為目標(biāo)函數(shù),其數(shù)學(xué)模型表達(dá)為

(36)

式中: 目標(biāo)函數(shù)為結(jié)構(gòu)位移u和聲壓p的實(shí)函數(shù);ρ=[ρ1,ρ2,…,ρNe]T為設(shè)計(jì)變量;Ne為設(shè)計(jì)變量總數(shù);ve為第e個(gè)單元的體積;fv為體積比約束。對于本文研究的聲振耦合問題,除了滿足上述的材料體積約束之外,還要滿足式(16)的控制方程。

3.2 穩(wěn)健拓?fù)鋬?yōu)化數(shù)學(xué)模型

與確定性拓?fù)鋬?yōu)化相比,穩(wěn)健拓?fù)鋬?yōu)化考慮了隨機(jī)變量對結(jié)構(gòu)響應(yīng)的影響,其目標(biāo)是尋找對隨機(jī)變量不敏感的優(yōu)化設(shè)計(jì),目標(biāo)函數(shù)的形式通常是隨機(jī)響應(yīng)的均值和其標(biāo)準(zhǔn)差的加權(quán)和,屬于多目標(biāo)優(yōu)化設(shè)計(jì)。其數(shù)學(xué)模型表述為

(37)

式中,k為隨機(jī)響應(yīng)標(biāo)準(zhǔn)差的權(quán)值因子。

3.3 材料插值模型

本文通過優(yōu)化雙材料的分布,在滿足約束的條件下達(dá)到減振降噪的效果。本文采用RAMP插值方法來描述雙材料的分布并建立設(shè)計(jì)變量ρ和材料分布的關(guān)系,可以將單元矩陣表示為

(38)

(39)

式中:Ke,Me分別為第e個(gè)單元的剛度矩陣、質(zhì)量矩陣;Ke1和Ke2,Me1和Me2是與分別給定的兩個(gè)材料相關(guān)的剛度矩陣和質(zhì)量矩陣;ρe=1為該單元完全由材料1(強(qiáng)材料)組成,ρe=0為該單元完全由材料2(軟材料)組成;η為讓中間密度趨近于0或1的懲罰因子,通常取5。

3.4 確定性條件下的靈敏度分析

確定性拓?fù)鋬?yōu)化的目標(biāo)函數(shù)對于設(shè)計(jì)變量ρe的導(dǎo)數(shù)可以表示為

(40)

(41)

式中,λ1,λ2為伴隨乘子。則目標(biāo)函數(shù)對于設(shè)計(jì)變量的靈敏度可以表示為

(42)

由于G,H只與頻率、幾何形狀有關(guān);Csf,Cfs,S只與幾何現(xiàn)狀有關(guān);均與設(shè)計(jì)變量無關(guān)。本文考慮的載荷fs也與設(shè)計(jì)變量無關(guān)。因此,式(42)可以簡化為

(43)

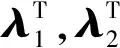
(44)

(45)

則,式(43)進(jìn)一步簡化為

(46)

3.5 隨機(jī)響應(yīng)的靈敏度分析

隨機(jī)響應(yīng)相對于設(shè)計(jì)變量的靈敏度也采用PCE方法進(jìn)行表示

(47)

式中,系數(shù)zi可根據(jù)與式(32)類似的方法獲得

(48)

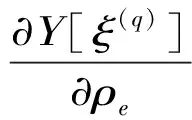
(49)

(50)

由此可得,穩(wěn)健拓?fù)鋬?yōu)化問題的目標(biāo)函數(shù)的靈敏度為

(51)

3.6 穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)流程

基于以上隨機(jī)響應(yīng)的靈敏度信息,采用MMA算法進(jìn)行設(shè)計(jì)變量更新。收斂條件為當(dāng)兩個(gè)相鄰迭代步的目標(biāo)函數(shù)的相對比值小于一個(gè)特定的常數(shù)τ

(52)

式中,Ji為第i步迭代對應(yīng)的目標(biāo)函數(shù)。本文中取τ=5.0×10-5。為了有效消除中間密度單元,使單元的相對密度趨近于0～1分布,本文采用保體積密度過濾方法[25],且將過濾半徑設(shè)為0.05 m。該過濾方法中的β參數(shù)會(huì)有效影響過濾的程度,β越大,過濾越明顯,但是β取值過大可能導(dǎo)致最終結(jié)果收斂至局部最優(yōu)解。本文中,在前20個(gè)迭代步,β=0;在迭代20步之后,迭代每增加一步,β增加0.5,最大不超過100。詳細(xì)的優(yōu)化過程如圖1所示。

圖1 聲振耦合系統(tǒng)穩(wěn)健拓?fù)鋬?yōu)化流程圖Fig.1 Flow chart of robust topology optimization of coupled structural-acoustic systems

4 數(shù)值算例

本章中,考慮水下立方殼在點(diǎn)激勵(lì)作用下的拓?fù)鋬?yōu)化問題。立方殼邊長為1 m,上表面為厚度0.02 m的四邊固支板,其余各面是剛性的。在上表面中心處有幅值為1 N的簡諧力作用,力的方向垂直于上表面豎直向下,如圖2所示。在殼的上表面劃分80×80的四節(jié)點(diǎn)板單元進(jìn)行結(jié)構(gòu)分析,對于聲場部分,在殼的每一個(gè)面采用40×40的四節(jié)點(diǎn)常量元進(jìn)行聲場分析。立方殼的外部介質(zhì)為水,其聲速為cf=1 482 m·s-1,密度為ρf=1 000 kg·m-3,不考慮立方殼內(nèi)部的耦合影響。

圖2 立方殼結(jié)構(gòu)Fig.2 The cubic shell

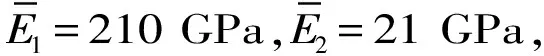
4.1 克服網(wǎng)格依賴性驗(yàn)證及體積約束影響測試

Sigmund等[26]指出采用獨(dú)立于網(wǎng)格的過濾技術(shù)可以克服網(wǎng)格依賴性問題。本文采用了保體積過濾技術(shù)進(jìn)行密度過濾,其過濾半徑是獨(dú)立于網(wǎng)格尺寸的。這里,我們先通過一個(gè)算例測試來說明本文的優(yōu)化方法是沒有網(wǎng)格依賴性問題的。以輻射聲功率級(jí)為目標(biāo)函數(shù),材料1的體積分?jǐn)?shù)約束fv=0.5;設(shè)計(jì)變量的初始值全部設(shè)置為1,即設(shè)計(jì)域全由材料1構(gòu)成。分別以80×80和60×60的結(jié)構(gòu)網(wǎng)格對在300 Hz激勵(lì)下的立方殼進(jìn)行拓?fù)鋬?yōu)化,最終得到的拓?fù)鋬?yōu)化結(jié)果如圖3所示。可以看出,采用不同網(wǎng)格密度進(jìn)行優(yōu)化,最終得到的拓?fù)浣Y(jié)構(gòu)是基本相同的。80×80和60×60網(wǎng)格的最終優(yōu)化結(jié)果對應(yīng)的輻射聲功率級(jí)分別為60.328 dB和60.340 dB, 相差很小。因此在本文中網(wǎng)格密度的差異不會(huì)對拓?fù)鋬?yōu)化的結(jié)果產(chǎn)生影響。本文后續(xù)算例將采用80×80的結(jié)構(gòu)網(wǎng)格進(jìn)行計(jì)算。

圖3 不同網(wǎng)格密度下的拓?fù)鋬?yōu)化結(jié)果Fig.3 Topology optimization results under different grid densities

為了說明體積約束分?jǐn)?shù)fv對優(yōu)化結(jié)果的影響,這里我們以輻射聲功率級(jí)為目標(biāo)函數(shù),分別在材料1的體積分?jǐn)?shù)約束fv取0.5,0.6,0.7時(shí)對300 Hz激勵(lì)下的立方殼進(jìn)行拓?fù)鋬?yōu)化。表1給出了不同體積分?jǐn)?shù)約束下的優(yōu)化結(jié)果對應(yīng)的輻射聲功率級(jí)以及優(yōu)化迭代步數(shù)。可以看出隨著fv的取值變大,輻射聲功率級(jí)是降低的,這是因?yàn)閺?qiáng)材料的剛度更大,強(qiáng)材料的應(yīng)用有利于降低振動(dòng)幅值,進(jìn)而降低輻射聲功率級(jí)。

表1 不同體積分?jǐn)?shù)約束fv下拓?fù)鋬?yōu)化結(jié)果對應(yīng)的輻射聲功率級(jí)和優(yōu)化迭代步數(shù)

4.2 隨機(jī)響應(yīng)分析的精度驗(yàn)證

在介紹穩(wěn)健拓?fù)鋬?yōu)化之前,我們先通過一個(gè)數(shù)值算例驗(yàn)證本文所用的PCE方法進(jìn)行隨機(jī)響應(yīng)分析的正確性。

我們選擇4階的PCE方法進(jìn)行隨機(jī)響應(yīng)分析,其中計(jì)算PCE系數(shù)過程中需要計(jì)算的積分,即式(33),我們通過5階Gauss-Hermite積分的張量積格式進(jìn)行計(jì)算。表2給出了當(dāng)設(shè)計(jì)域全為材料1時(shí),即全為強(qiáng)材料時(shí),采用PCE方法分別在頻率為50 Hz,100 Hz,150 Hz,200 Hz,250 Hz,300 Hz,400 Hz激勵(lì)下的輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差的計(jì)算結(jié)果,并將其與取10 000個(gè)樣本點(diǎn)下的蒙特卡洛方法(Monte Carlo method, MCM)得到的結(jié)果進(jìn)行比較。從表2結(jié)果可以看出,在以上所述的各個(gè)頻率激勵(lì)下,PCE方法得到的隨機(jī)響應(yīng)的均值和標(biāo)準(zhǔn)差和MCM得到的結(jié)果非常相近。由此可知,采用4階PCE方法可以獲得相當(dāng)精確的隨機(jī)響應(yīng)結(jié)果,因此在后續(xù)的穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)中使用PCE方法進(jìn)行隨機(jī)響應(yīng)分析是可靠的。

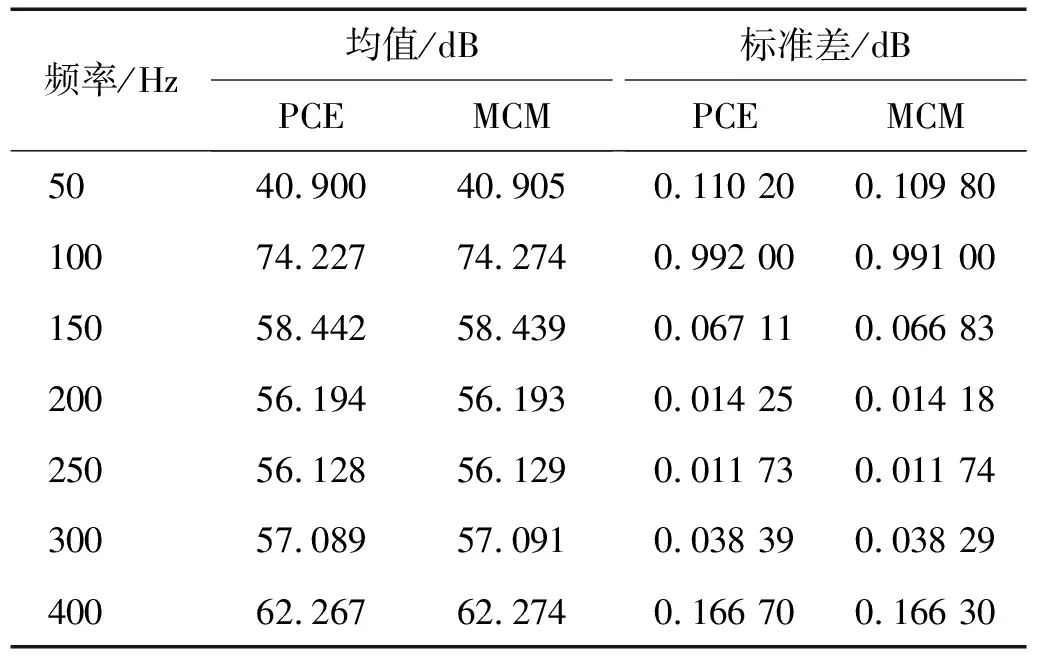
表2 PCE和MCM隨機(jī)響應(yīng)結(jié)果對比

4.3 穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)結(jié)果

首先對立方殼在300 Hz激勵(lì)下的情況進(jìn)行穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì),其目標(biāo)函數(shù)取輻射功率級(jí)的均值和標(biāo)準(zhǔn)差的加權(quán)和,如式(37)所示,其中權(quán)重因子k=3;材料1的體積分?jǐn)?shù)約束fv=0.5;設(shè)計(jì)變量的初始值全部設(shè)置為1,即設(shè)計(jì)域全由材料1構(gòu)成。在優(yōu)化44步迭代后目標(biāo)函數(shù)和體積約束函數(shù)收斂。目標(biāo)函數(shù)和體積約束以及輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差的迭代歷史如圖4所示。在最初的幾次迭代中,強(qiáng)材料的體積分?jǐn)?shù)從1降至0.5,并保持在0.5附近。由于我們設(shè)計(jì)變量的初始值全部設(shè)為1,目標(biāo)函數(shù)在開始時(shí)有很大的增加,但是在接下來的迭代中,目標(biāo)函數(shù)、均值、標(biāo)準(zhǔn)差基本在穩(wěn)定的減小,從而實(shí)現(xiàn)對材料分布不確定性的不敏感設(shè)計(jì)。穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)的輻射聲功率級(jí)的均值為60.336 dB,標(biāo)準(zhǔn)差為0.218 0 dB。為了體現(xiàn)穩(wěn)健優(yōu)化設(shè)計(jì)的優(yōu)越性,我們以輻射聲功率級(jí)作為目標(biāo)函數(shù),同樣基于RAMP材料插值模型和MMA算法進(jìn)行了確定性拓?fù)鋬?yōu)化設(shè)計(jì)。考慮材料性能的不確定性,對獲得的確定性拓?fù)鋬?yōu)化結(jié)果進(jìn)行隨機(jī)響應(yīng)分析,其輻射聲功率級(jí)的均值為60.351 dB,標(biāo)準(zhǔn)差為0.236 7 dB。穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)的輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差均小于確定性拓?fù)鋬?yōu)化結(jié)果,穩(wěn)健拓?fù)鋬?yōu)化結(jié)果比確定性拓?fù)鋬?yōu)化具有更好的隨機(jī)性能,并且對材料性能的不確定性不太敏感。穩(wěn)健拓?fù)鋬?yōu)化和確定性拓?fù)鋬?yōu)化的結(jié)果,如圖5所示。圖5中,黑色表示材料1,淺灰色表示材料2,兩者的結(jié)果僅有在一些細(xì)節(jié)上有所差別。

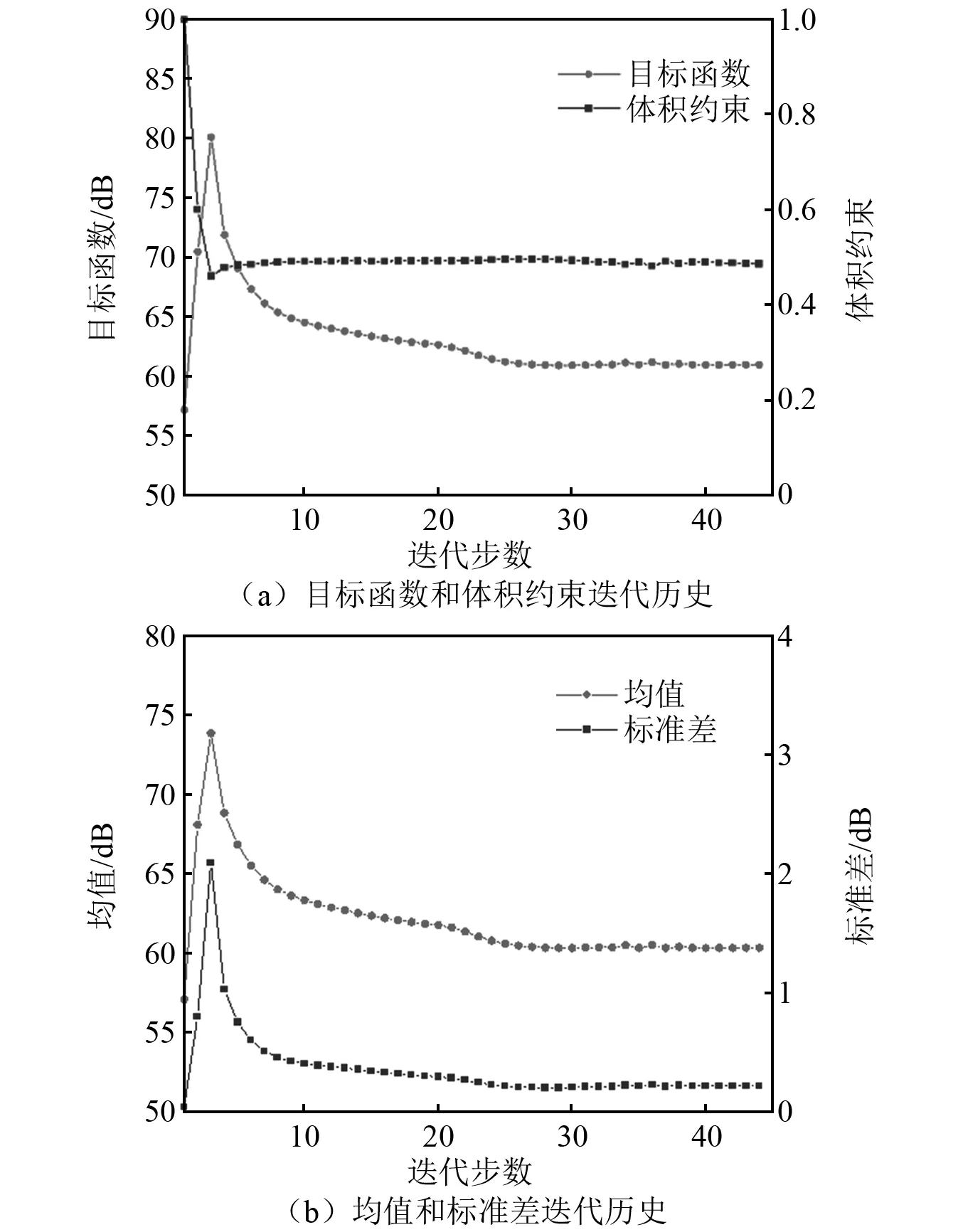
圖4 300 Hz激勵(lì)下穩(wěn)健拓?fù)鋬?yōu)化的迭代歷史Fig.4 Iterative history of robust topology optimization under 300 Hz excitation

圖5 300 Hz激勵(lì)下的穩(wěn)健優(yōu)化和確定性優(yōu)化結(jié)果Fig.5 Robust and deterministic optimization results under 300 Hz excitation

為了進(jìn)一步研究穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)的性能,我們在與上述相同的條件和參數(shù)下又對立方殼分別在200 Hz,250 Hz,400 Hz激勵(lì)下進(jìn)行了穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)和確定性拓?fù)鋬?yōu)化設(shè)計(jì)。圖6給出了相應(yīng)的確定性拓?fù)鋬?yōu)化和穩(wěn)健拓?fù)鋬?yōu)化的結(jié)果。其中200 Hz激勵(lì)下的穩(wěn)健拓?fù)鋬?yōu)化結(jié)果和確定性拓?fù)鋬?yōu)化僅在一些細(xì)節(jié)上存在差別,但是對于250 Hz和400 Hz,穩(wěn)健優(yōu)化拓?fù)浣Y(jié)果和確定性拓?fù)鋬?yōu)化存在明顯差異,這說明考慮材料彈性模量的不確定性對聲振系統(tǒng)的拓?fù)鋬?yōu)化結(jié)果有較大的影響,也說明考慮材料彈性模量的不確定性很有必要。為了更詳細(xì)地比較確定性優(yōu)化和穩(wěn)健優(yōu)化的結(jié)果,表3給出了在各個(gè)頻率激勵(lì)下穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)和確定性拓?fù)鋬?yōu)化設(shè)計(jì)對應(yīng)的輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差。可以看出,與確定性拓?fù)鋬?yōu)化相比,穩(wěn)健拓?fù)鋬?yōu)化結(jié)果的標(biāo)準(zhǔn)差都較小,這表明穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)對材料彈性模量的不確定性的敏感性更低,不僅如此,穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)的均值也都比確定性拓?fù)鋬?yōu)化的均值更低。

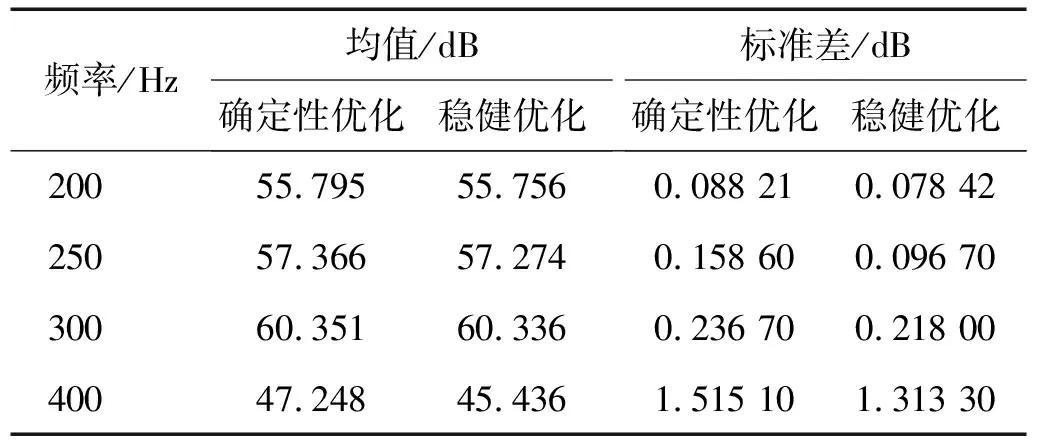
表3 確定性設(shè)計(jì)和穩(wěn)健設(shè)計(jì)的輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差

圖6 不同激勵(lì)頻率下的穩(wěn)健和確定性優(yōu)化結(jié)果Fig.6 Robust and deterministic optimization results at different excitation frequencies

為了研究穩(wěn)健拓?fù)鋬?yōu)化的目標(biāo)函數(shù)中的標(biāo)準(zhǔn)差的權(quán)值因子k對優(yōu)化結(jié)果的影響,以5種不同的權(quán)重因子對在400 Hz激勵(lì)下的水下立方殼進(jìn)行穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì),其他參數(shù)設(shè)置均相同。表4中給出了采用不同權(quán)值穩(wěn)健拓?fù)鋬?yōu)化結(jié)果對應(yīng)的輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差。結(jié)果顯示優(yōu)化結(jié)果的輻射聲功率級(jí)的均值隨著權(quán)值因子k的逐漸增大而增大,標(biāo)準(zhǔn)差逐漸減小,這和雙準(zhǔn)則優(yōu)化問題帕累托解的基本特征是吻合的。同時(shí)也表明隨著權(quán)值因子k的增大,目標(biāo)函數(shù)中標(biāo)準(zhǔn)差的權(quán)重變得更大,有利于降低優(yōu)化結(jié)果對材料彈性模量的不確定性的敏感性。圖7給出了k取1,2,4,5時(shí)的穩(wěn)健拓?fù)鋬?yōu)化結(jié)果,k取3時(shí)的結(jié)果已在圖6(e)中給出。從這些穩(wěn)健優(yōu)化得到的結(jié)果上可以看出,不同的權(quán)值因子k得到的優(yōu)化結(jié)果存在明顯的差異。綜上所述,權(quán)值因子k對優(yōu)化結(jié)果有較大的影響,選擇合適的權(quán)值因子k對于穩(wěn)健優(yōu)化設(shè)計(jì)至關(guān)重要。

表4 400 Hz激勵(lì)下不同權(quán)值因子k下的穩(wěn)健設(shè)計(jì)對應(yīng)的輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差

圖7 400 Hz激勵(lì)下不同權(quán)值因子k的穩(wěn)健優(yōu)化結(jié)果Fig.7 Robust optimization results of different weight factors k under 400 Hz excitation

為了研究兩材料彈性模量的變異系數(shù)的影響,在其他參數(shù)保持不變的情況下,以4種不同的變異系數(shù)γ對在400 Hz激勵(lì)下的立方殼進(jìn)行了穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì),目標(biāo)函數(shù)中的權(quán)重因子k都取3。圖8給出了變異系數(shù)為0.06,0.16,0.25時(shí)對應(yīng)的穩(wěn)健拓?fù)鋬?yōu)化結(jié)果,γ=0.10對應(yīng)的優(yōu)化結(jié)果已在圖6(e)給出。當(dāng)不確定性較小時(shí)(γ=0.06),穩(wěn)健拓?fù)鋬?yōu)化結(jié)果和確定性拓?fù)鋬?yōu)化結(jié)果較為相近,隨著變異系數(shù)的增大,穩(wěn)健拓?fù)鋬?yōu)化結(jié)果和確定性拓?fù)鋬?yōu)化的差異也越來越大。表5中給出了變異系數(shù)γ取不同值時(shí),穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)對應(yīng)的輻射聲功率級(jí)對應(yīng)的均值和標(biāo)準(zhǔn)差。

表5 400 Hz激勵(lì)下不同變異系數(shù)γ下的穩(wěn)健設(shè)計(jì)對應(yīng)的輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差

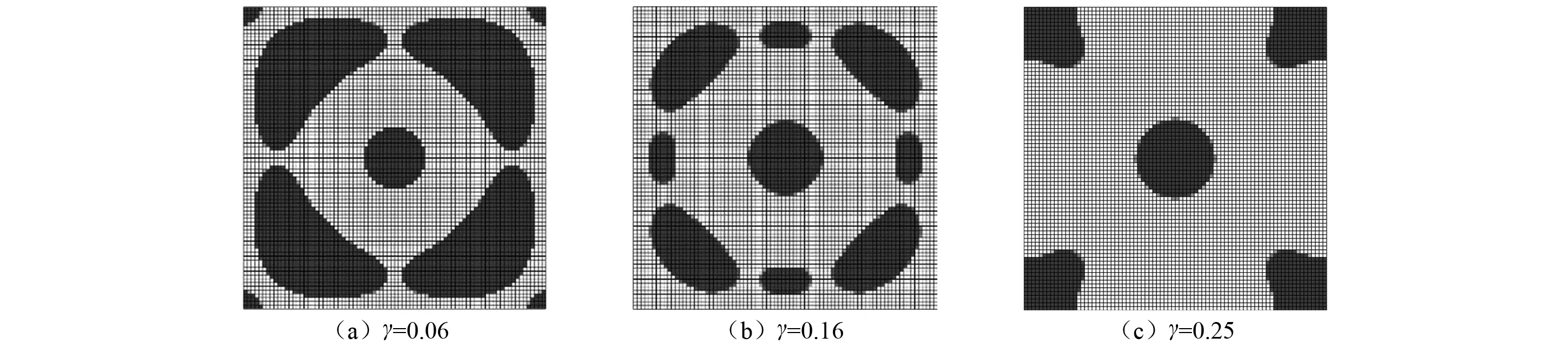
圖8 400 Hz激勵(lì)下不同變異系數(shù)γ下的穩(wěn)健優(yōu)化結(jié)果Fig.8 Robust optimization results with different coefficients of variation γ under 400 Hz excitation

5 結(jié) 論

本文研究了考慮材料性能的不確定性情況下,外聲場與結(jié)構(gòu)強(qiáng)耦合情況下的穩(wěn)健拓?fù)鋬?yōu)化問題。通過隨機(jī)場模型描述兩材料的彈性模量的不確定性,采用EOLE方法將隨機(jī)場離散為有限個(gè)不相關(guān)的隨機(jī)變量;采用PCE方法進(jìn)行隨機(jī)響應(yīng)預(yù)估和隨機(jī)響應(yīng)的靈敏度分析;采用RAMP模型進(jìn)行密度插值,建立單元相對密度和彈性模量、材料密度之間的關(guān)系;穩(wěn)健拓?fù)鋬?yōu)化的目標(biāo)函數(shù)為輻射聲功率級(jí)的均值和標(biāo)準(zhǔn)差的加權(quán)和;采用MMA算法對優(yōu)化問題進(jìn)行更新迭代求解。數(shù)值結(jié)果表明:

(1) 由于采用了獨(dú)立于網(wǎng)格尺寸的過濾方法,提出的拓?fù)鋬?yōu)化方法沒有網(wǎng)格依賴性問題。

(2) 與確定性拓?fù)鋬?yōu)化設(shè)計(jì)相比,穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)對應(yīng)的輻射聲功率級(jí)的標(biāo)準(zhǔn)差更低,實(shí)現(xiàn)了對材料性能不確定性更加不敏感的設(shè)計(jì),證實(shí)了本文建立的考慮材料性能不確定性的穩(wěn)健拓?fù)鋬?yōu)化模型的有效性。

(3) 隨著權(quán)值因子k的增大,穩(wěn)健拓?fù)鋬?yōu)化設(shè)計(jì)的輻射聲功率級(jí)的均值逐漸增大,標(biāo)準(zhǔn)差逐漸減小,且權(quán)值因子k對穩(wěn)健拓?fù)鋬?yōu)化結(jié)果的影響也較大。選擇合適的權(quán)值因子k很重要。