在問題解決中促進(jìn)模型觀念的形成與發(fā)展*
——以一道二次函數(shù)題的教學(xué)研究為例

杜育林 顧祥芳 劉光建

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022 年版）》（以下簡(jiǎn)稱“新課標(biāo)”）指出，學(xué)生核心素養(yǎng)主要包括會(huì)用數(shù)學(xué)的眼光觀察現(xiàn)實(shí)世界、會(huì)用數(shù)學(xué)的思維思考現(xiàn)實(shí)世界、會(huì)用數(shù)學(xué)的語(yǔ)言表達(dá)現(xiàn)實(shí)世界三個(gè)方面，并且明確了初中階段核心素養(yǎng)的九大主要表現(xiàn)。

案例：種植花草問題

某學(xué)校門前有一個(gè)邊長(zhǎng)為4m 的正方形花壇，花壇內(nèi)部要種植紅、黃、紫三種顏色的花草（如下頁(yè)圖1），圖中AE=MN。計(jì)劃在陰影部分的四個(gè)全等三角形內(nèi)種植紅色花草，在白色部分的四個(gè)全等三角形內(nèi)種植黃色花草，在小正方形MNPQ內(nèi)種植紫色花草。每種花草的價(jià)格如下表：

品種___價(jià)格（元/m2）紅色花草60黃色花草80紫色花草_120____

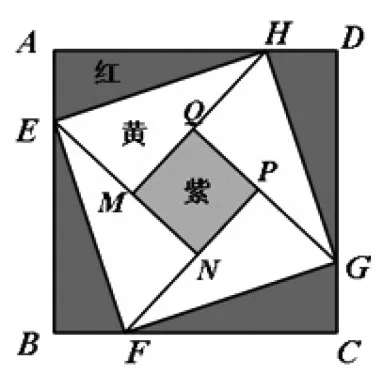
（圖1）

設(shè)AE的長(zhǎng)為xm，正方形EFGH的面積為Sm2，買花草的費(fèi)用為W元。

解答下列問題：

（1）S與x之間的函數(shù)表達(dá)式為S=_______；

（2）求W與x之間的函數(shù)表達(dá)式，并求出所需的最低費(fèi)用是多少元？

（3）當(dāng)買花草所需費(fèi)用最低時(shí)，求EM的長(zhǎng)。

教師在針對(duì)現(xiàn)階段初中生進(jìn)行音樂教學(xué)的過程中，應(yīng)全面利用音樂產(chǎn)生情感共鳴的特性對(duì)學(xué)生進(jìn)行相關(guān)的引導(dǎo)教育，確保學(xué)生在接受音樂知識(shí)的基礎(chǔ)上保證學(xué)生綜合素質(zhì)的建設(shè)。

一、設(shè)計(jì)意圖

新課標(biāo)在“課程目標(biāo)”中提出了三條義務(wù)教育階段的“總目標(biāo)”，其中第二條是讓學(xué)生“體會(huì)數(shù)學(xué)知識(shí)之間、數(shù)學(xué)與其他學(xué)科之間、數(shù)學(xué)與生活之間的聯(lián)系，在探索真實(shí)情境所蘊(yùn)涵的關(guān)系中，發(fā)現(xiàn)問題和提出問題，運(yùn)用數(shù)學(xué)和其他學(xué)科的知識(shí)與方法分析問題和解決問題”［1］11。為達(dá)此目標(biāo)，在數(shù)學(xué)教學(xué)中，教師應(yīng)結(jié)合具體課程內(nèi)容，精心設(shè)計(jì)案例，引導(dǎo)學(xué)生經(jīng)歷“問題情境—建立模型—求解驗(yàn)證”的過程，在這個(gè)過程中讓學(xué)生獲得“四基”“四能”，不斷提高學(xué)生通過建立數(shù)學(xué)模型解決實(shí)際問題的能力。

二次函數(shù)就是一個(gè)典型的數(shù)學(xué)模型，許多數(shù)學(xué)問題（含實(shí)際問題）都可以通過建立二次函數(shù)模型加以解決。新課標(biāo)在“課程內(nèi)容”中針對(duì)“二次函數(shù)”提出了四條具體要求，其中之一是“會(huì)求二次函數(shù)的最大值或最小值，并能確定相應(yīng)自變量的值，能解決相應(yīng)的實(shí)際問題”［1］57。

在學(xué)生學(xué)習(xí)了二次函數(shù)的概念、探究得到二次函數(shù)的性質(zhì)之后，為了在二次函數(shù)的應(yīng)用課中加強(qiáng)對(duì)學(xué)生應(yīng)用意識(shí)的培養(yǎng)，促進(jìn)模型觀念的形成和發(fā)展，我們?cè)O(shè)計(jì)了上面的案例。

二、教學(xué)目標(biāo)

1.引導(dǎo)學(xué)生經(jīng)歷“問題情境—建立模型—求解驗(yàn)證”的過程，獲得利用二次函數(shù)解決實(shí)際問題的經(jīng)驗(yàn)，感受模型思想和數(shù)學(xué)的應(yīng)用價(jià)值，進(jìn)一步促進(jìn)學(xué)生模型觀念的形成。

2.能分析和表示實(shí)際背景下變量之間的二次函數(shù)關(guān)系，并解決簡(jiǎn)單問題中與二次函數(shù)有關(guān)的部分。

3.在建立模型解決問題的過程中，培養(yǎng)并提高學(xué)生發(fā)現(xiàn)和提出問題、分析和解決問題的能力，增強(qiáng)應(yīng)用意識(shí)。

三、解答過程

本案例以“種植花草”為背景，設(shè)有三個(gè)問題。解答問題（1）只需要利用勾股定理求出正方形EFGH的邊長(zhǎng)即可。解答問題（2）應(yīng)分三步：一是求出種植各種花的面積，認(rèn)真觀察圖1，正確用含x的代數(shù)式表示三種花草的種植面積是關(guān)鍵；二是根據(jù)種植三種花草的面積和價(jià)格，正確列出所需費(fèi)用W與x的關(guān)系式，并進(jìn)一步整理得到函數(shù)關(guān)系式W=80x2-160x+1280（數(shù)學(xué)模型）是解決本小題的關(guān)鍵一步；三是利用二次函數(shù)的性質(zhì)求出函數(shù)W=80x2-160x+1280 的最小值，并根據(jù)實(shí)際問題的意義確定出最終答案。解答問題（3）的關(guān)鍵是在Rt△EMH中，利用勾股定理建立方程模型a2+（a+1）2=10。具體解答過程如下。

（1）根據(jù)勾股定理易求出正方形EFGH的邊長(zhǎng)，所 以S與x之間的函數(shù)表達(dá)式為S=x2+（4-x）2。

（2）W=60×4S△AEH+80×（S正方形EFGH-S正方形MNPQ）+120×S正方形MNPQ=60×4×（4-x）+80×［x2+（4-x）2-x2］+120x2=80x2-160x+1280=80（x-1）2+1200（0＜x＜4）。

當(dāng)x=1時(shí)，W有最小值1200。

由實(shí)際問題的意義可知，函數(shù)W=80x2-160x+1280的最小值就是實(shí)際問題的最小值。

（3）當(dāng)買花草所需的費(fèi)用W最低時(shí)，x=1，即AE=1m，所以AH=3m、EH2=AE2+AH2=10m2。

設(shè)EM=am，又MN=AE=1m，所以MH=（a+1）m，在Rt△EMH中，a2+（a+1）2=10，解得a=。因?yàn)閍＞0，所以，因此EM的長(zhǎng)為。

四、教學(xué)價(jià)值分析

從數(shù)學(xué)教育教學(xué)的角度看，本題的核心立意于“模型觀念”的形成與發(fā)展。事實(shí)上，本題不僅僅有助于模型觀念的培養(yǎng)，對(duì)于其他核心素養(yǎng)表現(xiàn)也具有積極的教育教學(xué)價(jià)值。

1.培養(yǎng)學(xué)生的運(yùn)算能力

數(shù)學(xué)離不開運(yùn)算。數(shù)學(xué)運(yùn)算能力是新課標(biāo)提出的核心素養(yǎng)之一，是指“根據(jù)法則和運(yùn)算律進(jìn)行正確運(yùn)算的能力”。運(yùn)算能力是在運(yùn)用數(shù)學(xué)知識(shí)進(jìn)行計(jì)算、推理以及解決問題的過程中逐漸形成并得到不斷提高的。

本案例有三問，每一問都考查了學(xué)生的運(yùn)算能力：第（1）問，為了寫出S與x之間的函數(shù)表達(dá)式，需要先根據(jù)勾股定理求出正方形EFGH的邊長(zhǎng)；第（2）問，為了求“所需費(fèi)用的最小值”，需要先根據(jù)二次函數(shù)的性質(zhì)求出二次函數(shù)的最小值，這里對(duì)函數(shù)表達(dá)式進(jìn)行變形整理變成了關(guān)鍵的一步，需要學(xué)生具備相應(yīng)的運(yùn)算能力；第（3）問，根據(jù)勾股定理建立起一元二次方程后，解方程的過程比較復(fù)雜，也要求學(xué)生具有較強(qiáng)的運(yùn)算能力。可見，本案例對(duì)于培養(yǎng)學(xué)生的運(yùn)算能力有積極的教學(xué)價(jià)值，是一道培養(yǎng)學(xué)生數(shù)學(xué)運(yùn)算能力的好題目。

2.在數(shù)學(xué)建模過程中感悟模型思想、提升模型觀念

“模型觀念”是新課標(biāo)提出的重要概念，是初中九大核心素養(yǎng)之一。為了分析本案例對(duì)學(xué)生模型觀念的形成與發(fā)展的作用，我們有必要澄清“數(shù)學(xué)模型”“數(shù)學(xué)建模”“模型思想”“模型觀念”等概念的意義。

“數(shù)學(xué)模型”就是根據(jù)特定的研究目的，采用形式化的數(shù)學(xué)語(yǔ)言，去抽象地、概括地表征所研究對(duì)象的主要特征、關(guān)系所形成的一種數(shù)學(xué)結(jié)構(gòu)。用字母、數(shù)字及其他符號(hào)建立起來(lái)的代數(shù)式、關(guān)系式、方程、函數(shù)、不等式，各種圖表、圖形等都是數(shù)學(xué)模型。［2］用通過計(jì)算得到的數(shù)學(xué)模型的結(jié)果來(lái)解釋實(shí)際問題，并接受實(shí)際的檢驗(yàn)，這個(gè)建立數(shù)學(xué)模型并應(yīng)用的全過程就稱為數(shù)學(xué)建模。

“模型思想”是指能夠有意識(shí)地用數(shù)學(xué)的概念、原理和方法，理解、描述以及解決現(xiàn)實(shí)世界中一類問題的那種思想。［3］史寧中教授認(rèn)為，數(shù)學(xué)基本思想有三種，模型思想便是其中之一。“模型觀念”主要是指對(duì)運(yùn)用數(shù)學(xué)模型解決實(shí)際問題有清晰的認(rèn)識(shí)［1］10，是通過建立數(shù)學(xué)模型去認(rèn)識(shí)問題、解決問題的自覺意識(shí)和思維方式。

本案例屬于典型的建立二次函數(shù)模型解答實(shí)際問題的案例（從解答過程看，還需要建立一元二次方程模型）。學(xué)生通過解答本案例，完整地經(jīng)歷了“問題情境—建立模型—求解驗(yàn)證”的過程，這個(gè)“建立模型—解決問題”的過程可用下頁(yè)圖2 表示。學(xué)生每經(jīng)歷一次圖2 所示的數(shù)學(xué)建模過程，其模型觀念都將得到一次增強(qiáng)和發(fā)展的機(jī)會(huì)。［4］

（圖2）

3.有利于學(xué)生形成良好的情感價(jià)值觀

新課標(biāo)對(duì)于“總目標(biāo)”提出的第三條要求是“對(duì)數(shù)學(xué)具有好奇心和求知欲，了解數(shù)學(xué)的價(jià)值，欣賞數(shù)學(xué)美，提高學(xué)習(xí)數(shù)學(xué)的興趣，建立學(xué)好數(shù)學(xué)的信心，養(yǎng)成良好的學(xué)習(xí)習(xí)慣，形成質(zhì)疑問難、自我反思和勇于探索的科學(xué)精神”［1］11。我們可以把這一條簡(jiǎn)稱為“情感價(jià)值觀”，這條目標(biāo)是在落實(shí)前兩條目標(biāo)的過程中實(shí)現(xiàn)的，即它是“伴隨”在學(xué)生獲取“四基”、形成“四能”以及“發(fā)現(xiàn)問題—提出問題—分析問題—解決問題”的過程中逐漸形成的。

學(xué)生在解答本題的過程中，不僅提高了分析問題、解決問題的能力，并且還培養(yǎng)了細(xì)致、嚴(yán)謹(jǐn)?shù)膶W(xué)習(xí)品質(zhì)。學(xué)生面對(duì)三個(gè)問題的計(jì)算過程都要細(xì)心、不可馬虎，在對(duì)二次函數(shù)通過配方得到W=80（x-1）2+1200 的過程，以及最后解方程更要精心運(yùn)算，一不小心就容易出錯(cuò)，這些運(yùn)算過程都有助于學(xué)生養(yǎng)成良好的學(xué)習(xí)習(xí)慣。

本題的真實(shí)情境背景有助于學(xué)生理解“數(shù)學(xué)來(lái)源于生活，數(shù)學(xué)服務(wù)于生活”的含義，在這個(gè)過程中，學(xué)生能進(jìn)一步形成模型觀念，提高分析問題解決問題的能力，不斷增強(qiáng)應(yīng)用意識(shí)。

五、教學(xué)啟示

我們常說某人有沒有“數(shù)學(xué)頭腦”，實(shí)際上就是指他能否運(yùn)用數(shù)學(xué)方法來(lái)解難答疑，歸根結(jié)底是指模型觀念的有、無(wú)、強(qiáng)、弱的問題。學(xué)生發(fā)現(xiàn)問題、提出問題、分析問題和解決問題的能力主要是在數(shù)學(xué)學(xué)習(xí)以及運(yùn)用數(shù)學(xué)知識(shí)解決問題的過程中得到提升的，新課標(biāo)中強(qiáng)調(diào)的應(yīng)用意識(shí)和模型觀念素養(yǎng)都是在“建立模型—解決問題”的過程中逐步形成的。

模型觀念是在經(jīng)歷“過程”中逐步形成與發(fā)展起來(lái)的，數(shù)學(xué)中建立模型內(nèi)容的“載體”處處皆是。在引導(dǎo)學(xué)生學(xué)習(xí)這些“載體”內(nèi)容（如方程、不等式、函數(shù)等）時(shí)，有兩個(gè)環(huán)節(jié)對(duì)于學(xué)生模型觀念的形成與發(fā)展具有積極的促進(jìn)作用：一是概念的建立過程；二是建立模型解決實(shí)際問題的過程。

這就決定了在數(shù)學(xué)概念的教學(xué)中，教師一方面應(yīng)認(rèn)真研讀教材，充分理解編寫意圖，并閱讀與本概念有關(guān)的教學(xué)論文（著）；另一方面要清楚數(shù)學(xué)概念常用的定義方式，確定給出本概念究竟要采用的哪一種定義方式。在此基礎(chǔ)上，教師要對(duì)教材內(nèi)容進(jìn)行二次加工處理，設(shè)計(jì)出問題系列，以此引導(dǎo)學(xué)生經(jīng)歷“知識(shí)背景—知識(shí)形成—揭示聯(lián)系”的過程，在這個(gè)過程中不斷提高學(xué)生的數(shù)學(xué)抽象能力、推理能力以及分析問題和解決問題的能力，進(jìn)一步感悟模型思想，增強(qiáng)模型觀念。