一種基于部分威力試驗數據的飛散角計算方法

李泓江，曹 濤，胡鵬順，蔡辰忱

(63876部隊，陜西 華陰 714200)

0 引言

威力試驗主要包括破碎性試驗、扇形靶試驗和靜態飛散角試驗,一般用于評定和研究殺傷爆破彈丸(簡稱殺爆彈)利用爆炸產生的高速破片與爆炸沖擊波對目標的毀傷[1],其中破片殺傷效應占據主導地位[2]。

破碎性試驗是測定榴彈破片質量分布的一種有效試驗方法。通常將彈丸放在一個空容器的中央,周圍放置使破片減速的介質,爆炸后回收破片并按質量分組,從而得到在不同質量范圍內的破片數[3]。文中使用的是水介質破碎性試驗水池回收破片,使用酒精清洗后晾干稱重。扇形靶試驗是測試彈丸擊穿破片殺傷半徑的一種常用試驗方法[4-5],爆炸后破片向四周飛散并穿過松木靶面,通過統計松木靶內破片穿透數,得出擊穿破片殺傷半徑。靜態飛散角試驗是戰斗部爆炸后,在戰斗部軸線平面內,以質心為頂點所作的包含有效破片90%的錐角[6],也就是破片飛散途中包含有效破片90%的兩線之夾角。

目前國內外對飛散角的計算仿真和試驗測試已有較多的研究。申景田等[7]采用直線排列的鋼靶板測量破片數量和空間分布,統計出占總破片數85%以上的殺傷帶,根據破片著靶位置和彈丸起爆點位置推算出飛散角;劉武等[8]采用ANSYS/LSDYNA建立有限元模型,結合流固耦合算法,對破片飛散角進行研究;李茂等[9]通過開展TNT裝藥驅動軸向預制破片飛散試驗,獲得預制破片飛散角參數,然后運用LS-DYNA軟件對驅動過程進行數值模擬;MOXNES等[10]對戰斗部鋼殼的斷裂和飛散進行了試驗,并采用不同模型進行模擬研究。經統計分析,目前基于破碎性、擊穿破片殺傷半徑等威力試驗數據,計算出飛散角方法的相關文獻較少。

文中以殺爆彈為樣本,開展試驗獲得威力試驗數據,計算不同質量級別破片的終點速度及飛行距離,用Origin軟件擬合破片飛行距離與破片數的曲線。通過殺傷密度建立飛散角與擊穿破片殺傷半徑之間的關系,基于部分威力試驗數據計算飛散角理論值。理論結果與試驗結果進行對比分析。

1 破片飛行理論

1.1 破片終點速度

根據破片質量mf,殺傷標準動能E,可以得滿足動能要求的最低速度vL:

(1)

1.2 破片初始速度

破片初始速度(初速)是衡量戰斗部殺傷作用的重要數據,因此進行理論計算時要盡可能的準確。影響破片初速的因素很多,為簡化問題,做以下幾點假設:

1)假定爆轟是瞬時的,破片加速為瞬時;

2)爆轟產物線性分布忽略爆轟產物沿裝藥軸向飛散;

3)殼體為等壁厚且爆炸后形成的破片具有相同的速度;

4)忽略殼體破裂阻抗,炸藥能量全部轉化為破片動能和爆轟產物動能,沒有能量耗散;

5)不考慮端部效應[11]。

對于文中所要研究的圓柱形彈丸,應使用哥耐(Gurney)公式[12]:

(2)

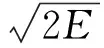
1.3 破片飛行距離

破片的運動方程[13]為:

(3)

(4)

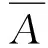
雖然cx在實際中是變化的,但在某一速度區間內可近似用一常數表示。對大部分破片的幾何形狀來說,cx隨速度變化的規則相似。為了限制區間劃分對計算結果產生的影響,在馬赫數取0.1～20的范圍內分為14個區間。vai和vei表示第i區間速度上、下限。

假設x=0時,速度為vf0,則第i區間破片飛行的距離xi,可根據式(3)求出:

(5)

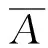
(6)

式中Kp為破片形狀系數。破片形狀系數主要通過試驗方法來獲取,對于球形、方形預制破片,其Kp取3.07～3.09;對于柱形預制破片,其Kp取3.35;對于菱形預制破片,其Kp取3.2～3.6;對于長方形預制破片,其Kp取3.3～3.8;對于不規則破片,其Kp取4.5～5.0。通過觀察殺爆彈樣本的破碎性回收破片,大部分破片為不規則形狀,極少部分破片為菱形或長方形,因此,此處破片形狀系數Kp取4.5(不規則)。

處理破碎性試驗威力數據,按照相關標準統計出每一質量范圍內的破片數,繪制破片質量分布曲線、破片累積個數與破片質量關系曲線。

通過上述計算,得出某一質量破片的初速與末速,在速度衰減的整個過程中,劃分出如表1的速度區間,可得在某一區間的飛行距離,所有區間飛行距離相加得到此破片整個飛行距離,從而繪制不同質量級別破片與飛行距離的關系曲線。結合破碎性試驗威力數據,繪制破片累積個數與飛行距離的關系曲線,用Origin軟件擬合得到累積破片數與飛行距離關系函數。

表1 速度區間Table 1 Velocity interval Ma

2 威力數據的關系

2.1 靜態飛散角對應曲面面積

靜態飛散角對應曲面面積定義為:以質心為球面球心,以對應半徑為球面半徑,用包含有效破片90%的兩直線以彈軸為軸線旋轉一周,將球面切割為兩個圓形曲面和一個環帶狀曲面三個部分,其中環帶狀曲面為兩直線所夾靜態飛散角對應曲面,如圖1所示。

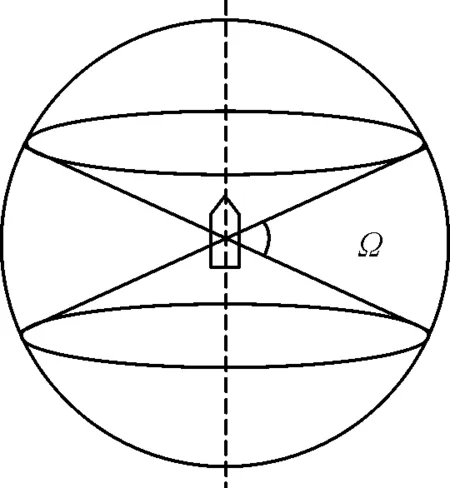
圖1 靜態飛散角對應曲面面積示意圖Fig.1 Diagram of a surface with static scattering angles

其對應面積和投影距離公式為:

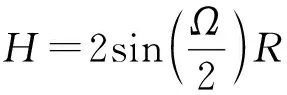
(7)

式中:SR為靜態飛散角對應曲面面積;R為球面半徑;H為環帶狀曲面在彈軸上的投影距離;Ω為靜態飛散角度。

2.2 擊穿殺傷半徑

采用扇形靶試驗方法,通過統計破片擊穿靶板的結果,來計算擊穿殺傷半徑RC。扇形靶用木材為干燥的三等松木板,厚度為25 mm±1 mm,布靶圓心角為30°或60°,即每塊扇形靶的扇面弧長,等于各扇形靶板所處圓周的1/6或1/12弧長,靶高為3 m。

2.3 威力數據之間的關系

擊穿破片數與對應殺傷面積之比為擊穿破片殺傷密度ρm,即擊穿破片數與靜態飛散角對應曲面面積存在如式(8)關系:

ρm=0.9Cm/SR

(8)

式中:ρm為殺傷密度;Cm為破片累積數;SR為靜態飛散角對應曲面面積。

根據擊穿破片殺傷半徑定義可知,當擊穿殺傷密度ρm=1/(1.5×0.5)時,其對應的半徑為擊穿破片殺傷半徑RC。將試驗值擊穿破片殺傷半徑代入,可得靜態飛散角理論數據值。

3 靜態飛散角的理論計算

3.1 擬合累積破片數與飛行距離關系

對殺爆彈開展破碎性試驗并回收破片稱重,按照相關標準統計出每一質量范圍內的破片數,區間破片質量取破片區間中數(如破片質量區間0.1～0.2 g,區間中數取0.15 g),處理數據后繪制破片質量分布曲線如圖2所示;破片累積個數與破片質量關系曲線如圖3所示。

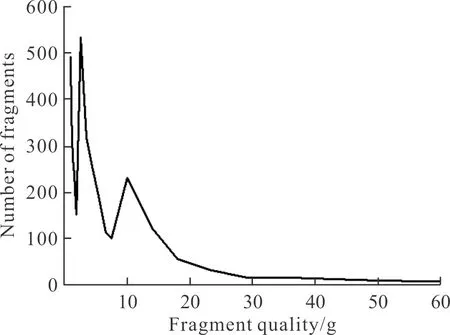
圖2 破片質量分布曲線Fig.2 Fragment mass distribution curve

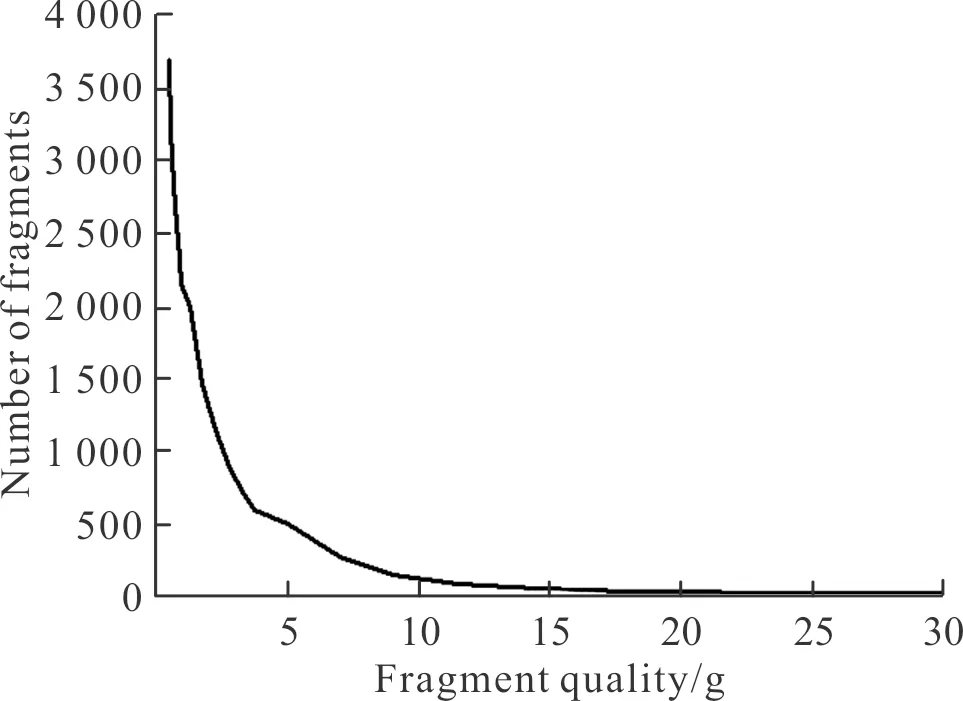
圖3 破片累積個數與破片質量關系曲線Fig.3 Relationship between the cumulative number of fragments and the mass of fragments

殺爆彈參數如表2所示。

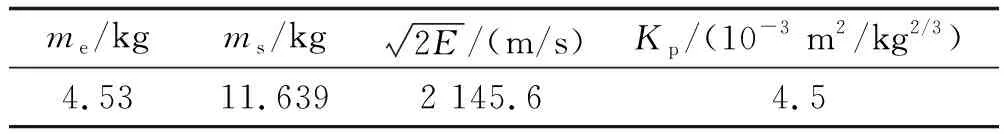
表2 殺爆彈參數Table 2 Parameters of the kill blasting projectile

文中動能E取98 J,空氣密度取1.29 kg/m3,根據式(1)～式(6)可繪制殺傷距離Ri與的破片質量mi關系曲線如圖4所示;破片累積個數Cm與飛行距離Rm的關系曲線及擬合曲線如圖5所示。

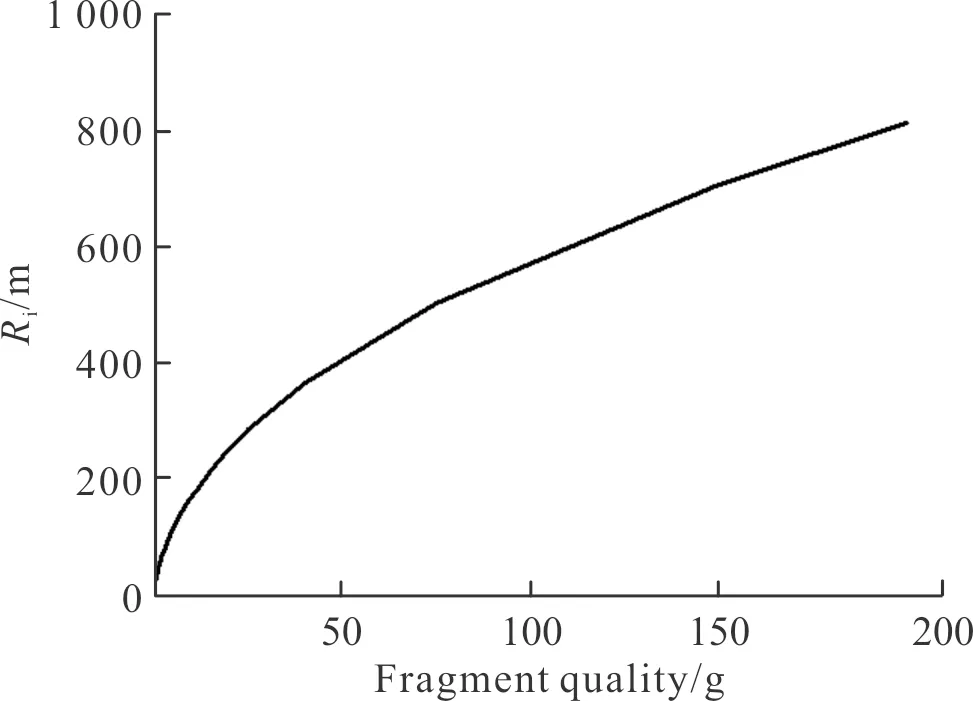
圖4 殺傷距離與破片質量關系曲線Fig.4 The relationship between killing distance and fragment mass

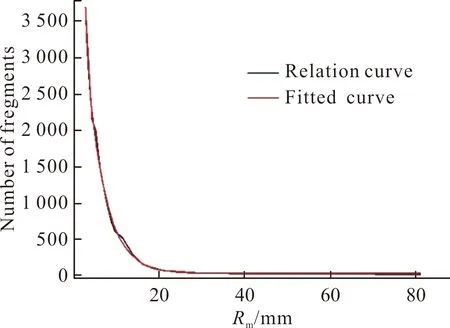
圖5 破片累積個數與飛行距離的關系曲線及擬合曲線Fig.5 The relationship curve and fitting curve between cumulative number of fragments and flight distance

破片累積個數Cm與飛行距離Rm擬合方程Cm(R)為:

Cm=11.6146+5855.05862×e(-R/43.08306)+
91106.56655×e(-R/4.76063)

(9)

其相關系數r=0.99861。

3.2 靜態飛散角理論威力數據值

將擊穿破片殺傷半徑試驗威力數據RC=34.1 m,代入式(9)中得Cm=2742.4。將RC、Cm代入式(7)、式(8)中,得到靜態飛散角理論威力數據值Ω′=14.66°。

4 結論

使用同一批生產的彈丸開展靜態飛散角試驗,采用直線排列的鋼靶板測量破片數量和空間分布。試驗結果顯示破片的空間分布廣泛,距離爆心較遠位置破片分布密度較小,經統計,在戰斗部軸線平面內,以質心為頂點所作的包含有效破片90%的錐角Ω=15°,對比數據分析可得:

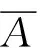
2)若破片形狀系數Kp取5.0(不規則),則同一質量等級破片飛行距離減少13.1%～38.7%,且破片質量越大,影響越大。因此在破碎性試驗回收破片并按質量分組環節,可以將破片,按照球形、方形、柱形、菱形、長條形及不規則形狀分類統計,按照不同形狀所占比例確定破片形狀系數Kp的取值,則理論計算更貼近試驗。

3)基于部分威力試驗數據的飛散角計算方法,計算得飛散角理論值,與試驗結果一致性較好。