中長周期波浪作用下的系泊船舶響應特性研究

劉擎波，譚忠華，沈文君*

（1.中交第一航務工程勘察設計院有限公司，天津 300220；2.交通運輸部天津水運工程科學研究所，天津 300456）

0 引言

隨著港口建設逐漸向深海及國外發展以及優質岸線的逐漸減少，擬建區域波浪條件的復雜性日益增加。非洲西部、拉美西部海域受長周期波影響較為明顯。國內外港口斷纜的事故時有發生，系泊的安全成為業內關注的重點問題之一。中長周期波由于波長較長，波能較大，且波浪周期接近船舶橫搖周期，因此容易對系泊船舶的泊穩造成較大影響[1]。近年來，諸多學者開始研究中長周期波作用對系泊船舶泊穩性影響。

早在20 世紀80 年代，楊憲章[2]針對受涌浪和長周期波影響嚴重的毛里塔尼亞友誼港，對波浪和系泊船舶運動進行了研究，研究指出，系泊船舶對低頻長周期波浪響應敏感，波列中的長周期波浪成分可引起船舶的劇烈運動，從而給碼頭系泊及裝卸作業造成危害；Hiraishi 等[3]基于日本北部Tomakomai 港集裝箱船橫搖側翻案例數據并結合實地觀測發現，由于中長周期波周期接近系泊船舶橫搖周期，故更易引起船舶橫搖共振，導致側翻事件頻發。史憲瑩等[4]采用物模試驗研究LNG船在雙峰譜中長周期波浪下運動響應特性，并探討了總能量相同，高低頻能量比例變化對系泊船舶運動響應的影響。研究發現系泊船舶運動響應幅度、系船纜張力極值取決于低頻波比例。沈雨生等[5]采用物理模型試驗對一艘10 萬噸級散貨船進行了不同周期下的系列試驗，研究結果表明，系泊船舶橫蕩運動量總體上隨著波浪周期的增大而增大，橫搖和升沉運動量隨著波周期的增大先增大后減小。宋偉華等[6]采用OPTIMOOR 軟件系統分析了周期、波高和入射角度對船舶系泊穩定的影響，研究結果表明，波高和入射角度對升沉運動的影響極為明顯，周期對船舶縱移運動影響最為明顯。沈文君等[7]采用數值方法對某駁船的運動特性開展了研究，分析了不同波浪作用角度、波浪周期，對系泊船舶與護舷、系泊纜繩組成的非線性耦合系統的響應規律。肖鑫等[8]采用Mike 21MA 軟件，分析了波高、周期以及波浪入射角度的系泊船舶運動的影響規律。

綜上所述，波浪周期對浮式結構物的作用非常明顯，對碼頭作業安全及運營可靠性產生不利影響。本文基于擬在秘魯建設的一座20 萬噸級散貨裝船碼頭展開研究，對停靠主力船型的耦合動力響應特性進行系統分析，研究成果可為設計提供借鑒和參考，具有一定的工程應用意義。

1 數值計算模型

基于BV 船級社的Hydrostar 軟件和Ariane 軟件進行分析。首先基于三維勢流理論，利用Hydorstar軟件在頻域內得到了研究船舶的水動力特性。然后通過頻時域轉換，在Ariane 軟件中建立船舶、系泊系統、護舷等組成的整體系統，通過求解該系統與外界環境載荷的聯合運動方程，在每個時間步長內數值求解公式，迭代計算船舶的位置、船舶與護舷的距離、系船柱與船上導纜孔的距離等，進而得到船舶六自由度的時間歷程響應、纜繩拉力的時間歷程響應以及護舷撞擊力的歷程響應。

1.1 船舶模型

計算所用船舶主尺度參數如表1 所示，模型如圖1 所示。

圖1 水動力網格模型Fig.1 Hydrodynamic mesh model

表1 船舶主尺度參數Table 1 Principal parameters of the barge

1.2 纜繩與護舷布置

擬建碼頭為樁基梁板結構，排架間距7.5 m，系船柱與護舷的布設間距均為15 m。船舶的系泊布置如圖2 所示，采用16 根纜繩系泊，其中艏艉纜各4 根、艏艉橫纜各2 根、艏艉倒纜各2 根，建模時每根纜繩單獨模擬，其中圖2（b）為系泊數學模型圖，圖中黑色圓點代表系船柱和護舷結構。計算纜繩材質為聚丙烯，直徑為75 mm，最小破斷力為816 kN，安全工作荷載為408 kN。護舷采用SCN 1800H 型號，設計反力為2 172 kN，共有21 個護舷與船舶接觸。纜繩和護舷的性能模擬曲線見圖3。

圖2 系泊布置方案圖（4∶2∶2）Fig.2 Mooring arrangement plan（4∶2∶2）

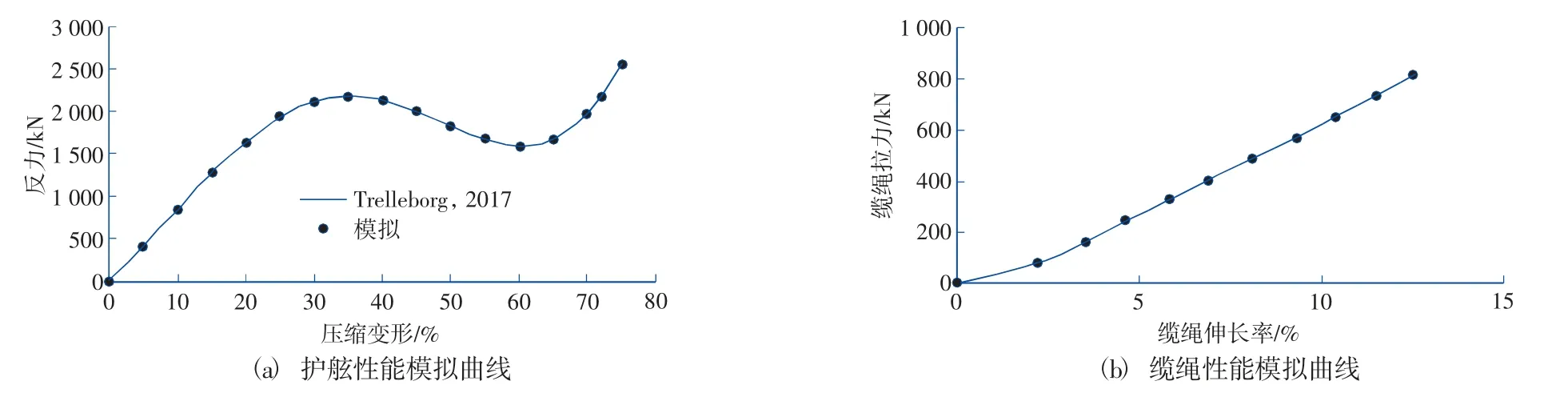
圖3 護舷和纜繩特性曲線Fig.3 Characteristics curve of fender and mooring lines

1.3 計算工況

工程區域波高玫瑰圖如圖4 所示，從圖中可以看出該區域的主要浪向為W 向，占全部波向的76.77%；其次為WNW 向，占全部波向的22.4%。有效波高主要集中在0.2～0.6 m 的范圍內，占90.34%，0.6～0.8 m 范圍內占7.49%，大于0.8 m有效波高占2.09%。譜峰周期主要介于11～17 s 之間，占全部的92.89%，其中13～15 s 占46.12%。可見工程海域波浪表現為中長周期涌浪。

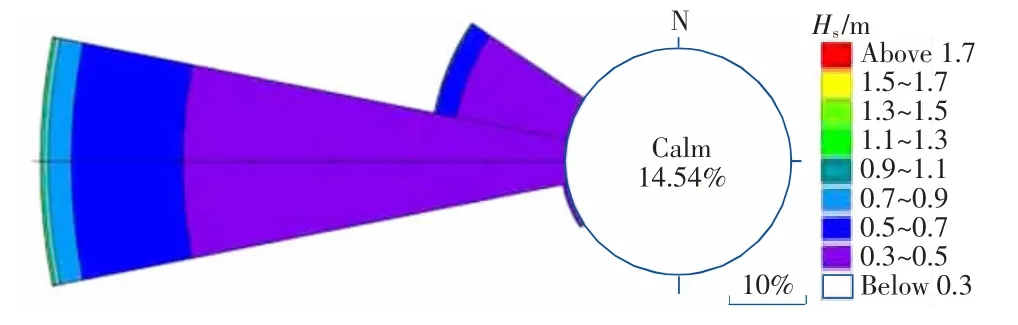
圖4 有效波高玫瑰圖（2017-07-01—2018-07-01）Fig.4 Rose diagram of significant wave height（from 01/07/2017 to 01/07/2018）

碼頭軸線方位為108°～288°，波浪入射方向與船舶縱軸線（艏方向）為±20°～±30°范圍內。按照不利情況考慮，具體計算條件如下：

1） 計算波向：與船舶縱軸線（艏方向）夾角呈30°；

2） 根據以往的經驗和本工程的波浪作用角度，11 s 以下的波浪周期對本工程的影響較小，因此本文重點關注的波浪要素取值如下：

譜峰周期Tp：13 s、15 s、17 s、19 s；

有效波高Hs：0.4 m、1.0 m；

系泊模擬時，采用的波譜為J 譜，譜峰因子取3.3。

1.4 極限標準

1） 運動量標準

參考PIANC 標準《Criteriaformovementofmoored ships in harbours-practical guide》[10]，專業化散貨泊位在進行裝船作業時，船舶的運動量應滿足：①縱蕩＜5.0 m；②橫蕩＜2.5 m；③艏搖＜3°；對垂蕩、橫搖、縱搖運動量無具體要求，六自由度運動示意如圖5 所示。

圖5 船體運動的六自由度示意圖Fig.5 Schematic diagram of six degrees of freedom for ship motion

2） 系纜力標準

試驗纜繩最大允許拉力，鋼纜不應超過纜繩破斷力的55%，其他纜繩不應超過纜繩破斷力的50%[11]。本次研究所用纜繩的最小破斷力為816 kN，因此，當纜繩拉力大于408 kN 時，認為超出安全作業范圍。

3） 撞擊力標準

對于護舷的撞擊力和撞擊能量，當試驗所得到的撞擊力和撞擊能量超過護舷的設計撞擊力和撞擊能量時，則認為護舷型號不滿足要求。

2 數值計算結果分析

2.1 計算結果初步分析

根據上述的計算組次，開展船舶系泊碼頭時的運動響應分析，纜繩預張力取10%的最小破斷力，即81.6 kN。用Hydrostar 水動力計算軟件計算平均慢漂力和水動力系數、一階波浪載荷傳遞系數，并在時域分析軟件Ariane 中考慮不同風浪流聯合作用下大量組次的運動時域分析，得到纜繩的受力時歷曲線，最后按照3 h 回歸周期得到船舶六自由度運動量和纜繩受力最大統計值。本文以船舶壓載狀態為例，給出了部分組次對應的六自由度運動量、系纜力的時歷曲線，如圖6、圖7 所示。

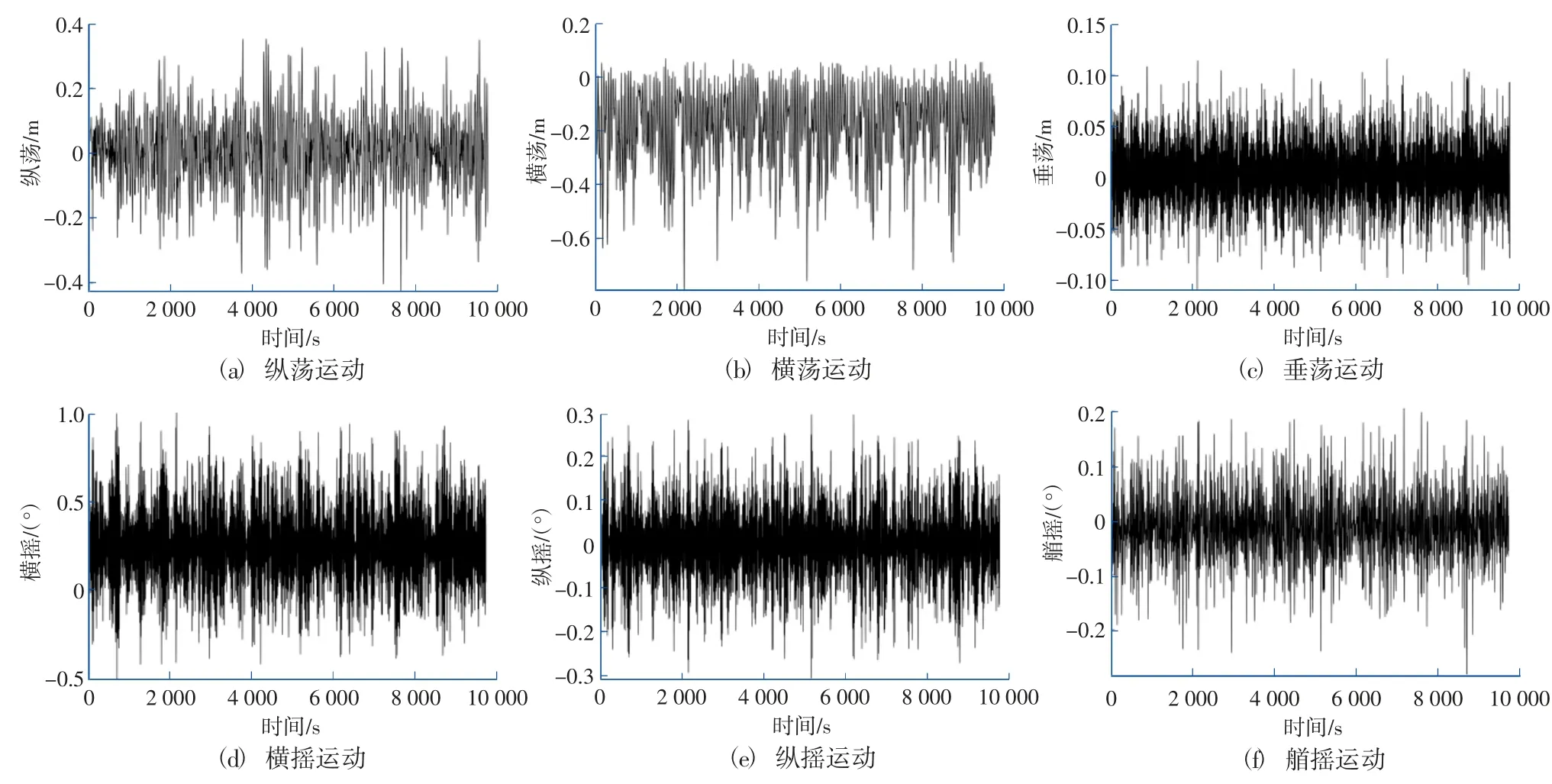
圖6 船舶運動時歷曲線（壓載Tp=13 s，Hs=1.0 m）Fig.6 Time history of ship motion（Ballast Tp=13 s，Hs=1.0 m）

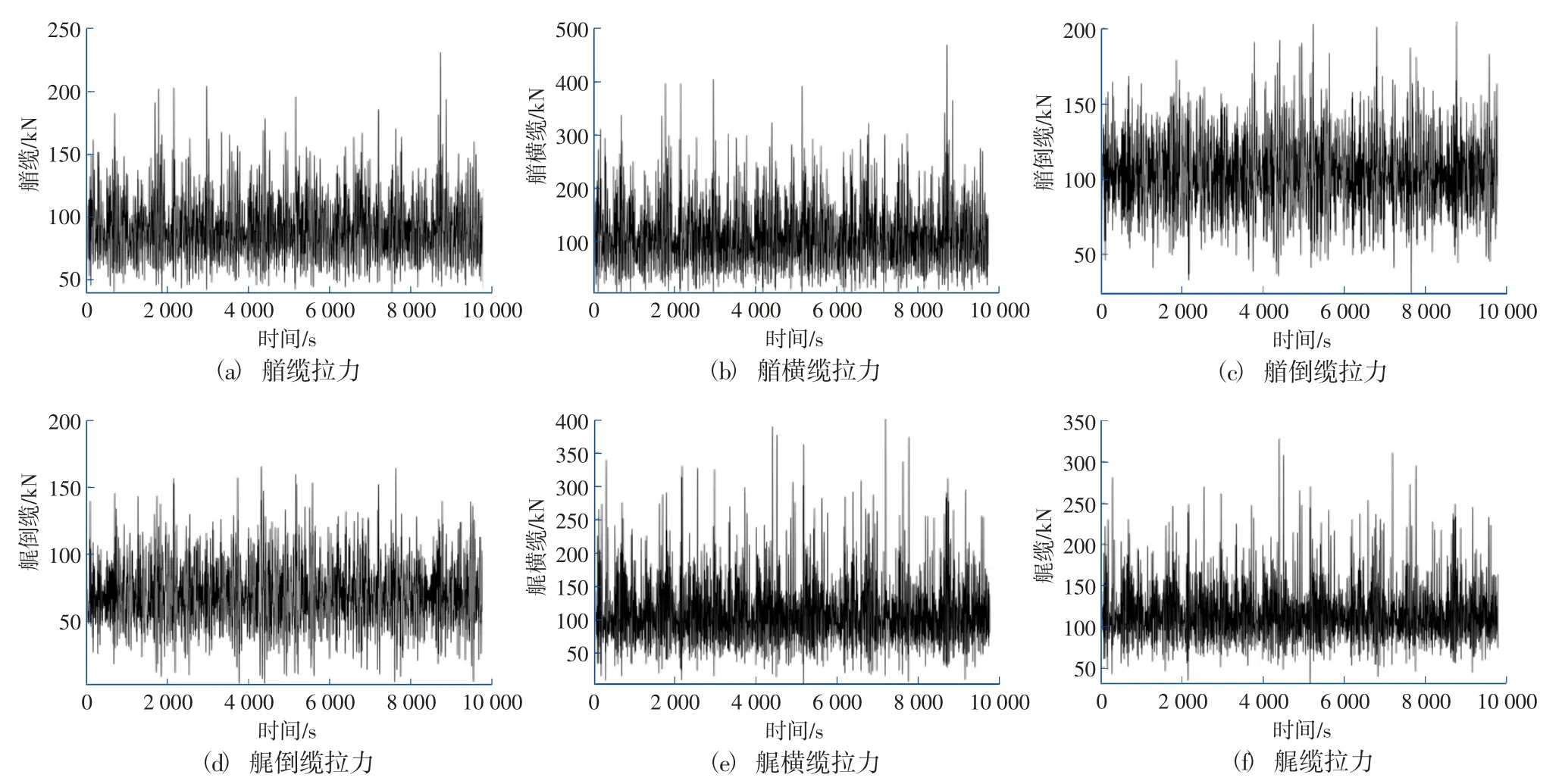
圖7 纜繩拉力時歷曲線（壓載Tp=13 s，Hs=1.0 m）Fig.7 Time history of mooring line tension（Ballast Tp=13 s，Hs=1.0 m）

從圖7 中可以看出，船舶壓載狀態下，在Tp=13 s、Hs=1.0 m 波浪作用下，船舶的運動量均在標準要求范圍內，但某些纜繩拉力不滿足作業要求。其中，艏橫纜、艉橫纜受力最大，其次是艏纜和艉纜，纜繩拉力最大值455 kN，超出了纜繩的安全工作標準。圖8 給出了計算工況下，每個護舷的撞擊力。從圖8 中可以看出，由于受到斜浪作用，艏、艉接觸的護舷撞擊力最大，中間區域受力最小，護舷最大撞擊力為1 116 kN，滿足護舷設計要求。根據JTS 165—2013《海港總體設計規范》，15 萬噸級散貨船在平均周期Tm≤8 s（Tp≤9.68 s）的順浪作用下時，建議裝船作業的允許波高為H4%=2.0 m（Hs=1.58 m）。由此可見，波浪周期對允許作業波高的影響非常明顯，若需要進一步分析允許的作業波高，則需降低波高繼續進行計算，直至得出的纜繩拉力小于對應的允許標準。

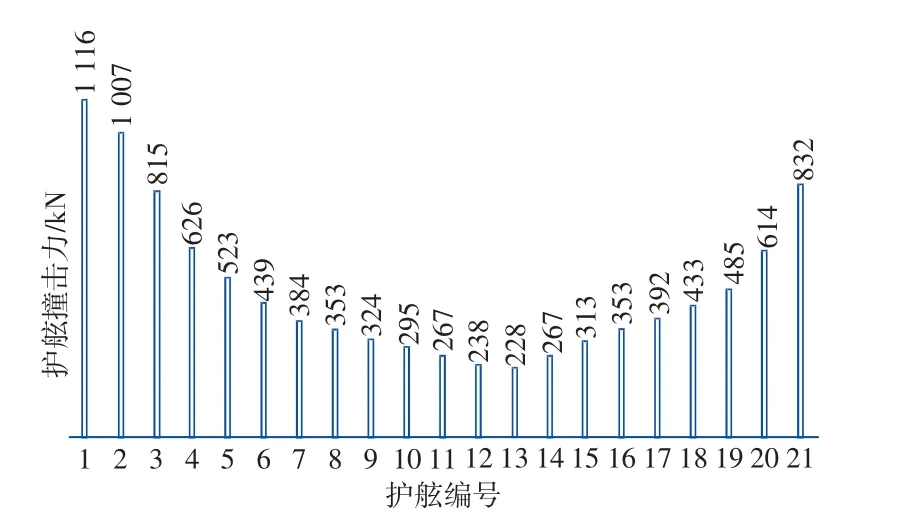
圖8 護舷最大撞擊力分布統計值（壓載Tp=13 s，Hs=1.0 m）Fig.8 Statistical value of maximum fender force（Ballast Tp=13 s，Hs=1.0 m）

2.2 裝載狀態和波浪周期對響應的影響規律

為了掌握不同波浪周期對系泊船舶的影響，選取Hs=0.4 m，Tp=13 s、15 s、17 s 和19 s 的工況進行計算分析，掌握滿載和壓載狀態下，六自由度運動量以及系纜力隨周期的變化規律，如圖9和圖10 所示。

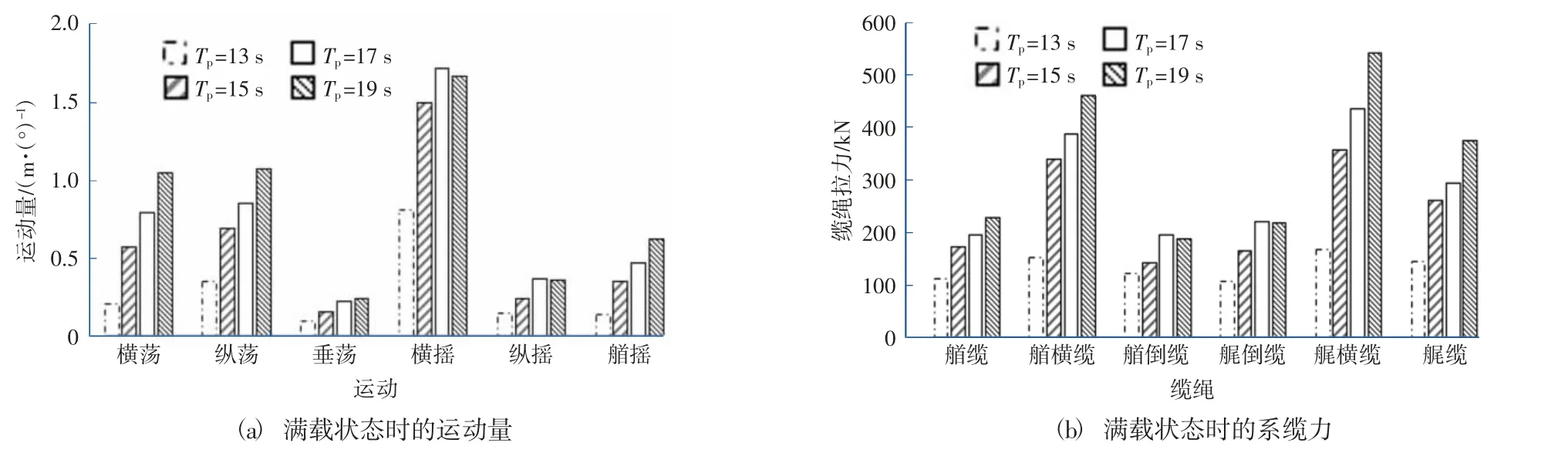
圖9 滿載狀態時的結果對比Fig.9 Comparison of results for laden condition

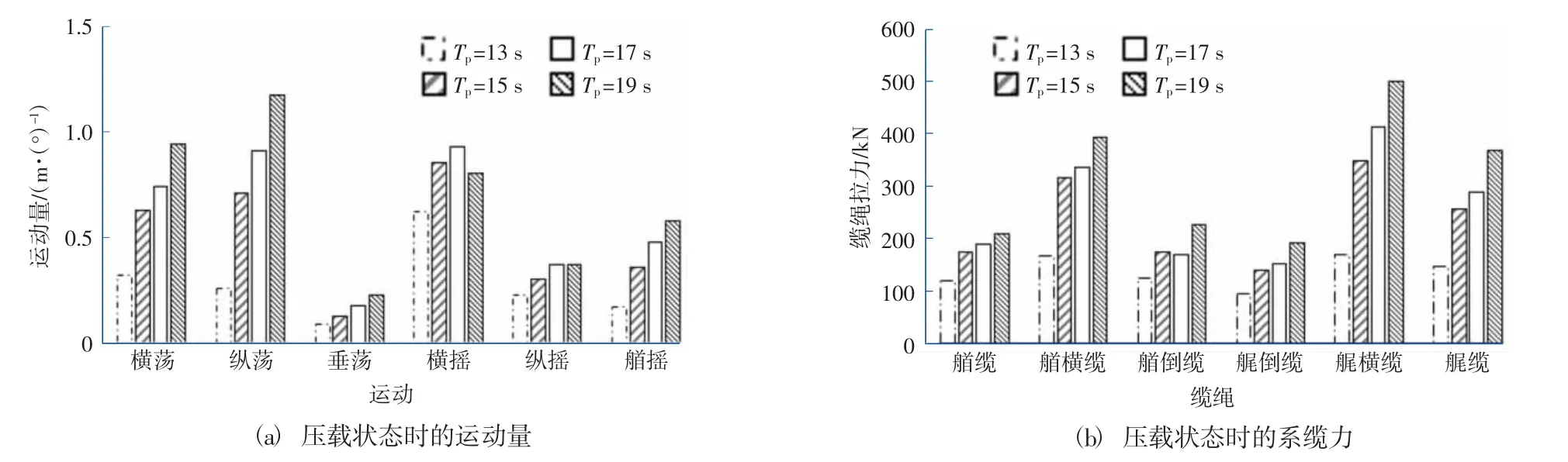
圖10 壓載狀態時的結果對比Fig.10 Comparison of results for ballast condition

從圖中可以看出：

1） 在滿載和壓載情況下，在30°波浪作用時，除橫搖運動外，其他5 個自由度的運動量基本都隨著周期的增大逐漸增大，譜峰周期17 s 時滿載的橫搖運動為1.71°，略大于15 s 和19 s 的數值；壓載的橫搖運動為0.93°，也略大于15 s 和19 s 的數值。

2） 在滿載和壓載情況下，纜繩拉力明顯隨著波浪周期的增大逐漸增大，且最大受力出現的位置均在艏橫纜和艉橫纜上。在相同周期波高作用下，滿載狀態下的纜繩受力略大于壓載狀態時的結果。

3 結語

為了掌握系泊船舶在中長周期波浪作用下的響應特性，本文基于船舶的系泊布置方案建立了船舶-纜繩-護舷的三維時域分析模型，分析了該耦合系統的運動響應特性，討論了不同周期以及不同裝載狀態對六自由度運動量、纜繩拉力等參數的影響規律，主要結論有以下幾點：

1） 在Tp=13 s、Hs=1.0 m 波浪作用下，船舶的運動量均在標準要求范圍內，在各組纜繩中，艏、艉橫纜受力最大，其次是艏纜和艉纜，纜繩拉力最大值455 kN，超出了纜繩的許用標準。

2） 工程主要受30°斜浪的作用，艏、艉接觸的護舷撞擊力最大，中間區域受力最小，護舷最大撞擊力為1 116 kN，滿足護舷設計要求。

3） 在滿載和壓載情況下，除橫搖運動外，其他5 個自由度的運動量基本都隨著周期的增大逐漸增大，譜峰周期Tp=17 s 時滿載和壓載的橫搖運動分別為1.71°和0.93°，略大于15 s 和19 s 的數值。

4） 在滿載和壓載情況下，纜繩拉力明顯隨著波浪周期的增大逐漸增大，且最大受力出現的位置均在艏橫纜和艉橫纜上。

5） 數值模擬計算結果表明，系泊系統的動力響應情況對長周期波浪的作用十分敏感。建議密切關注工程區域的波浪周期，以保障系泊作業的安全進行。