含柔性墊層的剛性擋土墻土壓力計(jì)算方法

梁利生 郭俊源 王慧芳

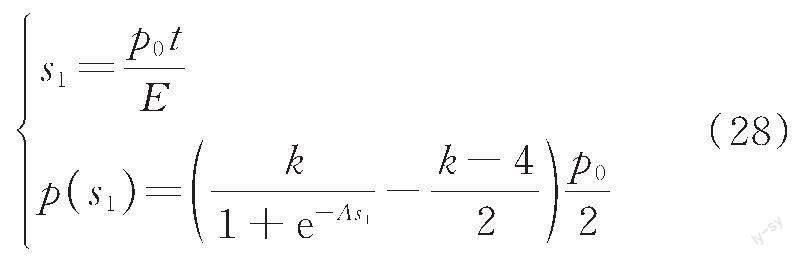
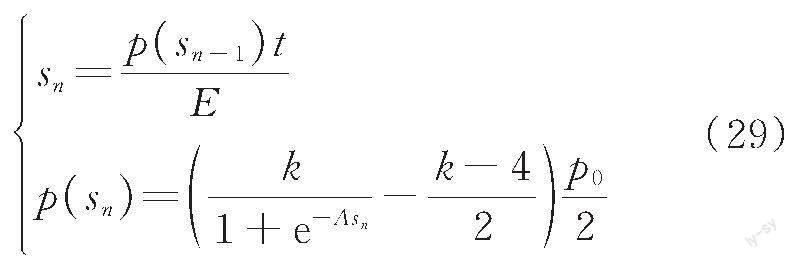
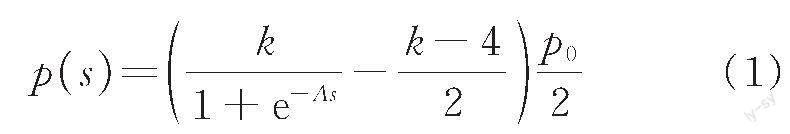
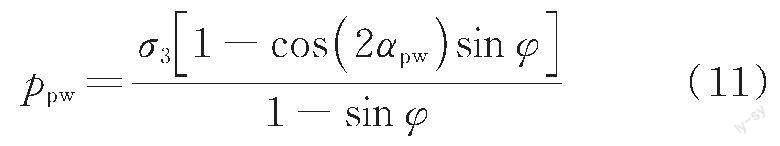
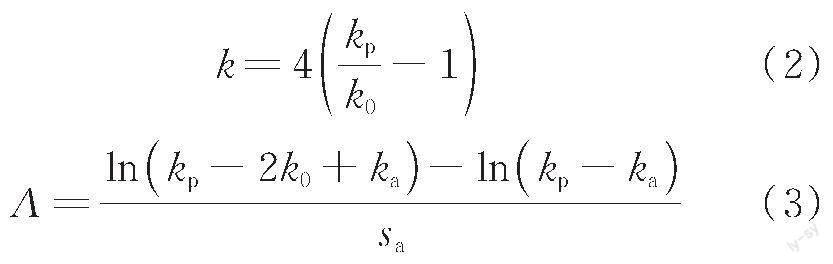
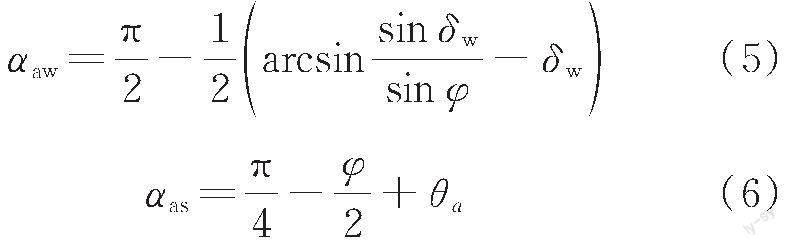
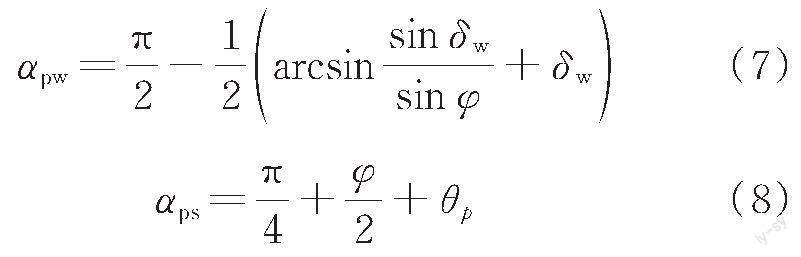
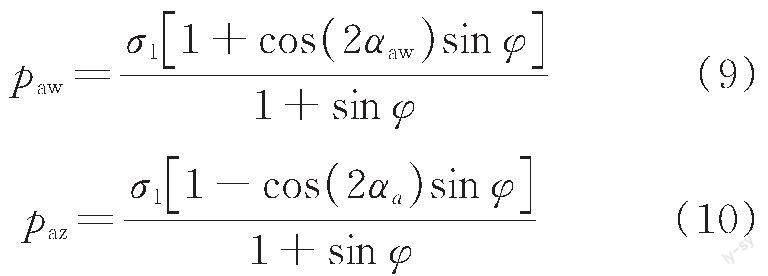
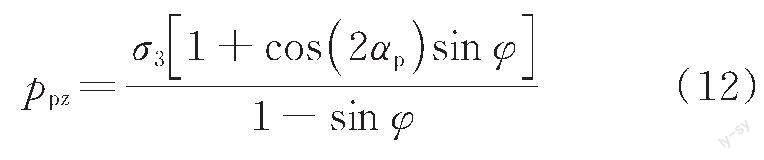
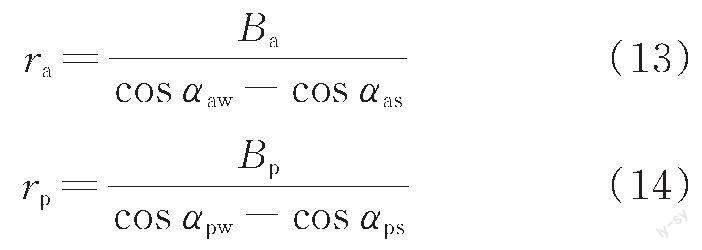
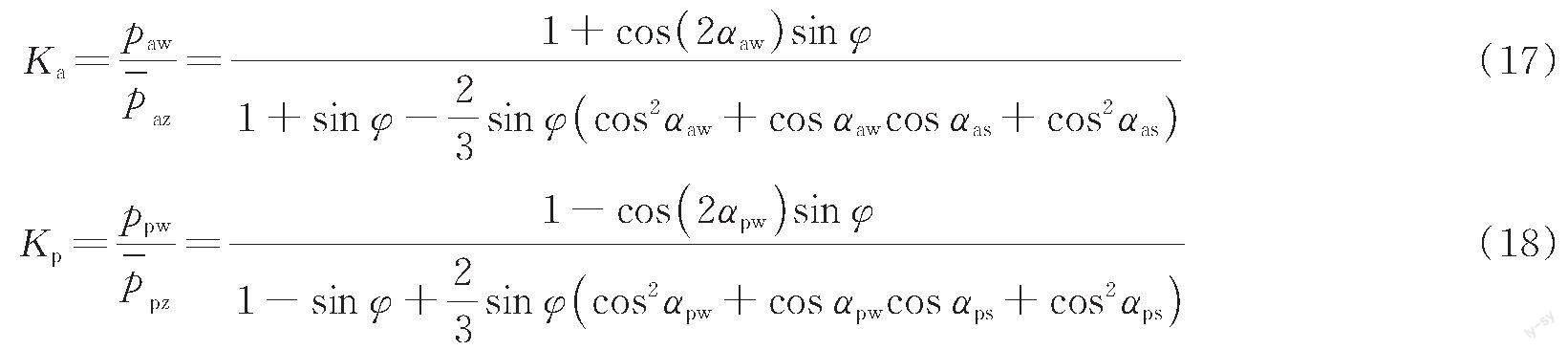
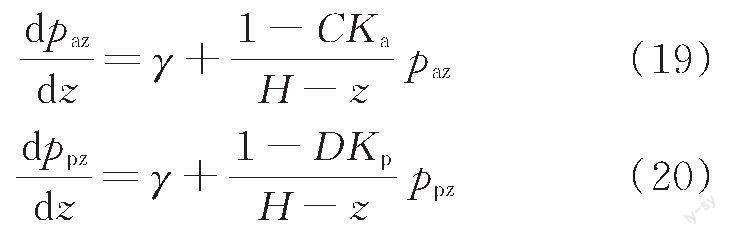
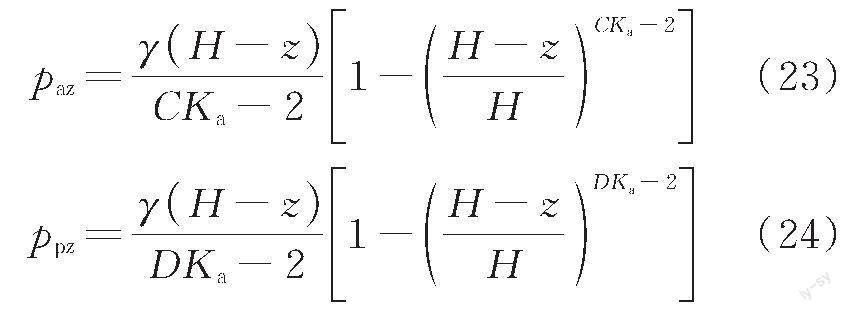
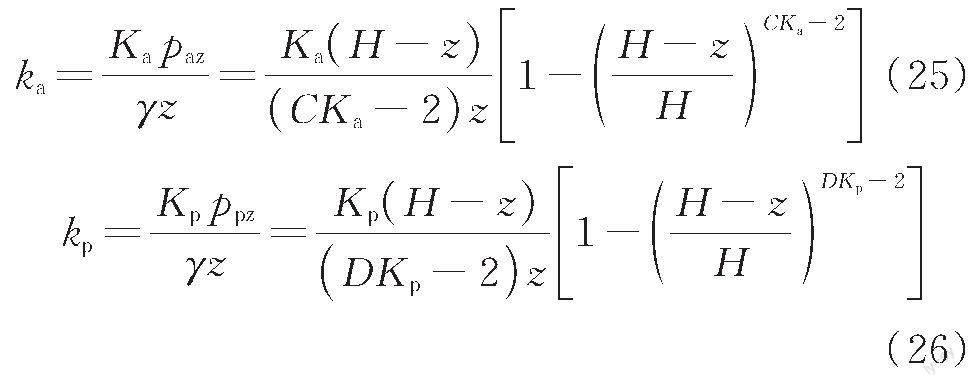
摘要：在剛性擋土墻與填土之間設(shè)置柔性墊層能減小作用于擋土墻的土壓力，但目前仍缺乏針對(duì)設(shè)置聚苯乙烯土工泡沫（EPS）柔性墊層的剛性擋土墻土壓力計(jì)算方法。將EPS柔性墊層的壓縮量視為墻后填土的位移量，考慮擋土墻后土拱效應(yīng)，基于擋土墻土壓力-位移的關(guān)系曲線，引入迭代法進(jìn)行收斂計(jì)算，得到設(shè)置EPS柔性墊層的剛性擋土墻土壓力計(jì)算方法。該計(jì)算方法的優(yōu)勢(shì)是可在EPS柔性墊層壓縮量未知的情況下求解土壓力，即可應(yīng)用工程設(shè)計(jì)階段。建立FLAC3D有限差分?jǐn)?shù)值模型，對(duì)推導(dǎo)的理論解進(jìn)行驗(yàn)證，并對(duì)EPS柔性墊層減載效果進(jìn)行分析。結(jié)果表明：基于土壓力-位移關(guān)系曲線并采用迭代法得出的墻后設(shè)置EPS柔性墊層的剛性擋土墻土壓力理論解具有較好的合理性。在EPS柔性墊層彈性模量不變的情況下，EPS柔性墊層減小土壓力的效果隨著EPS柔性墊層厚度的增加而增強(qiáng)；在EPS柔性墊層厚度一定的情況下，隨著EPS柔性墊層彈性模量的增加，其減小土壓力的效果逐漸減弱。

關(guān)鍵詞：擋土墻；EPS柔性墊層；土壓力；減載；土拱效應(yīng)

中圖分類號(hào)：TU476.4???? 文獻(xiàn)標(biāo)志碼：A???? 文章編號(hào)：2096-6717（2023）06-0158-07

Calculation for lateral earth pressure on rigid retaining wall with flexible cushion

LIANG Lisheng1， GUO Junyuan2， WANG Huifang1

（1. Department of Civil Engineering; The Cultivation Base of Shanxi Key Laboratory of Mining Area Ecological Restoration and Solid Wastes Utilization， Shanxi Institute of Technology， Yangquan 045000， Shanxi， P. R. China；2.College of Civil Engineering， Taiyuan University of Technology， Taiyuan 030024， P. R. China）

Abstract： The installation of polystyrene geofoam （EPS） inclusions between the rigid retaining wall and backfill can reduce the earth pressure acting on the retaining wall. To date， there is a lack of the calculation method for the earth pressure on rigid retaining walls with EPS inclusions. In this study， the compression from geofoam inclusions is equated to the displacement of the backfill， and the soil arching behind the retaining wall is considered. Based on the displacement-dependent earth-pressure model （DDEP）， the iterative method is introduced for the convergence calculation， and then the theoretical solution is obtained to calculate the earth pressure on the rigid retaining wall with EPS inclusion. The advantage of the proposed method is that it can be used to solve the earth pressure when the EPS compression ?modulus is not provided. A series of FLAC3D numerical models is established to verify the proposed method and analyze the load reduction effect of EPS inclusions. The proposed theoretical solutions based on the DDEP model and iterative method are in preferably consistency with the numerical results. Effect of EPS on reducing the earth pressure increases with increase of the thickness of EPS inclusions when EPS elastic modulus is constant， and decreases with increase of the elastic modulus of EPS inclusions while EPS thickness is constant.

Keywords： retaining wall； EPS flexible inclusion； earth pressure； load reduction； soil arching

擋土墻廣泛應(yīng)用于土木工程領(lǐng)域中，作用于擋土墻的側(cè)向土壓力計(jì)算是其設(shè)計(jì)的關(guān)鍵指標(biāo)。聚苯乙烯土工泡沫（EPS）是一種具有密度小、壓縮變形大、強(qiáng)度高和減振性能好等優(yōu)點(diǎn)的柔性材料。將EPS墊層設(shè)置于剛性擋土墻和填土之間后，EPS墊層受到的土壓力將會(huì)使其產(chǎn)生一定的壓縮量，該部分壓縮量即轉(zhuǎn)化為填土的位移。在剛性擋土墻自身位移量很小的情況下，設(shè)置EPS墊層后，擋土墻受到的土壓力將會(huì)明顯減小[1]。

已有諸多學(xué)者對(duì)設(shè)置EPS的剛性擋土墻開(kāi)展了研究。Bathurst等[2-3]開(kāi)展了室內(nèi)振動(dòng)臺(tái)試驗(yàn)研究不同密度的EPS緩沖層減小剛性擋土墻在動(dòng)荷載作用下的墻背土壓力的效果。Ikizler等[4]開(kāi)展針對(duì)墻后填土為膨脹土的EPS墊層減載試驗(yàn)，得出EPS墊層可減小水平壓力和豎向壓力。Ertugrul等[5-6]開(kāi)展了縮尺模型試驗(yàn)，得出EPS墊層的厚度和剛度對(duì)于土壓力的減小有主要影響。Ni等[7]開(kāi)展縮尺模型試驗(yàn)，分析EPS墊層的厚度與剛度對(duì)于減壓效果的影響。Kim等[8]基于模型試驗(yàn)建立FLAC數(shù)值模型，分析EPS墊層的材料類型和厚度對(duì)土壓力的影響，并提出剛性擋土墻后EPS墊層的分段設(shè)計(jì)方案。鄭俊杰等[9-11]開(kāi)展一系列模型試驗(yàn)，對(duì)EPS減載擋土墻土壓力的效果及擋土墻后EPS墊層的設(shè)計(jì)方案進(jìn)行了研究。謝明星等[12]建立設(shè)置EPS墊層的剛性擋土墻數(shù)值模型，分別對(duì)擋土墻后填土的靜止、主動(dòng)及被動(dòng)3種位移狀態(tài)進(jìn)行了研究。許曉亮等[13]通過(guò)開(kāi)展不同級(jí)別荷載下的模型試驗(yàn)，分析墻后鋪設(shè)EPS柔性墊層、回填泡沫輕量土及其同時(shí)施加時(shí)的墻后土壓力大小及分布特征。

目前，仍缺乏設(shè)置EPS墊層后剛性擋土墻土壓力的計(jì)算方法。筆者將EPS墊層的壓縮量視為墻后填土的位移量，基于Mei等[14]提出的擋土墻土壓力-位移的關(guān)系曲線，推導(dǎo)設(shè)置EPS墊層的剛性擋土墻土壓力的理論解。首先，考慮擋土墻后土拱效應(yīng)，推導(dǎo)出考慮土拱效應(yīng)的主動(dòng)和被動(dòng)土壓力系數(shù)；其次，將所推導(dǎo)的主動(dòng)和被動(dòng)土壓力系數(shù)代入土壓力-位移關(guān)系曲線，并將靜止土壓力作為初始狀態(tài)，引入迭代法進(jìn)行收斂計(jì)算，求解EPS的壓縮量和對(duì)應(yīng)的土壓力；最后，建立FLAC3D有限差分?jǐn)?shù)值模型，驗(yàn)證所得出理論解的合理性，并對(duì)EPS墊層減載效果進(jìn)行分析。

1 擋土墻土壓力-位移的關(guān)系曲線

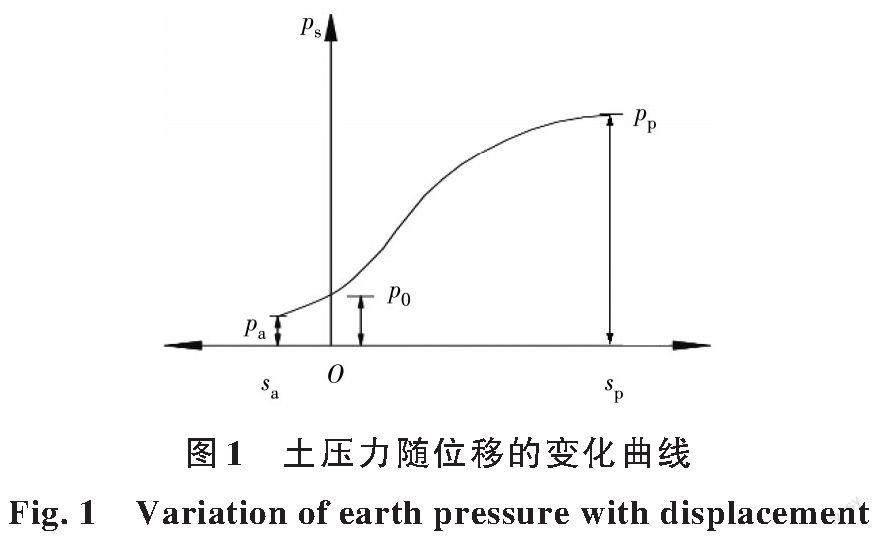
Mei等[14]將擋墻背離土體方向的位移記為負(fù)值、朝向土體方向的位移記為正值，假定存在一個(gè)函數(shù)p（s）可表示土壓力p和位移s之間的關(guān)系（圖1），則該函數(shù)p（s）滿足以下條件：

1）p（s）為單調(diào)遞增的函數(shù)。

2）p（s）函數(shù)存在上下限，下限為主動(dòng)土壓力pa及其對(duì)應(yīng)的位移sa，上限為被動(dòng)土壓力pp及其對(duì)應(yīng)的位移sp。

3）當(dāng)s=0時(shí)，p為靜止土壓力p0。

進(jìn)而基于上述條件提出土壓力-位移的關(guān)系曲線

其中

式中：k0、ka、kp分別為靜止、主動(dòng)、被動(dòng)土壓力系數(shù)。

2 考慮土拱效應(yīng)的土壓力系數(shù)

擋土墻無(wú)位移的情況下，目前最常用的土壓力系數(shù)計(jì)算方法為Jaky[15]針對(duì)粗粒土得出的半經(jīng)驗(yàn)半理論的靜止土壓力系數(shù)公式。

k0 = 1 - sin φ （4）

式中：φ為墻后填土的內(nèi)摩擦角。

在墻后填土達(dá)到主動(dòng)或被動(dòng)狀態(tài)過(guò)程中，由于擋土墻墻背并非絕對(duì)光滑，擋土墻與填土之間存在的摩擦作用必將引起土體應(yīng)力偏轉(zhuǎn)，形成土拱效應(yīng)，從而對(duì)土壓力的分布產(chǎn)生影響。為便于計(jì)算，研究基于以下假定：

1）擋土墻為剛性擋土墻，且擋土墻墻背垂直；

2）擋土墻與基巖之間的填土為無(wú)黏性土，符合Mohr-Coulomb破壞準(zhǔn)則，且不考慮孔隙水作用；

3）土壓力求解視為平面應(yīng)變條件下的二維問(wèn)題；

4）對(duì)于剛性擋土墻，其自身的位移量通常非常小。因此，忽略擋土墻的位移量，將EPS墊層的壓縮量視為墻后填土的位移；

5）考慮土拱效應(yīng)時(shí)，主動(dòng)狀態(tài)下填土的小主應(yīng)力軌跡線和被動(dòng)狀態(tài)下的大主應(yīng)力軌跡線均假定為圓弧形。

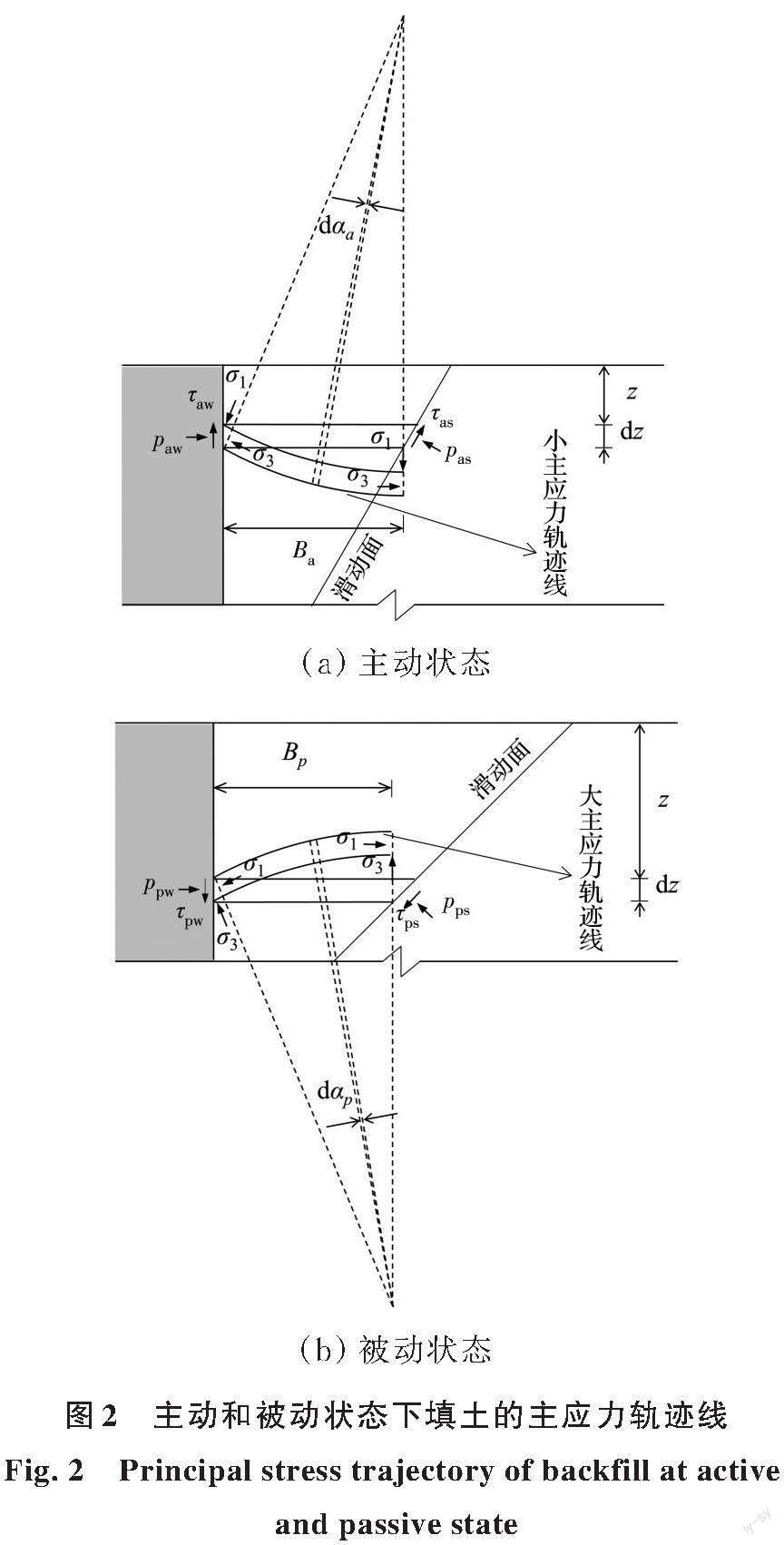
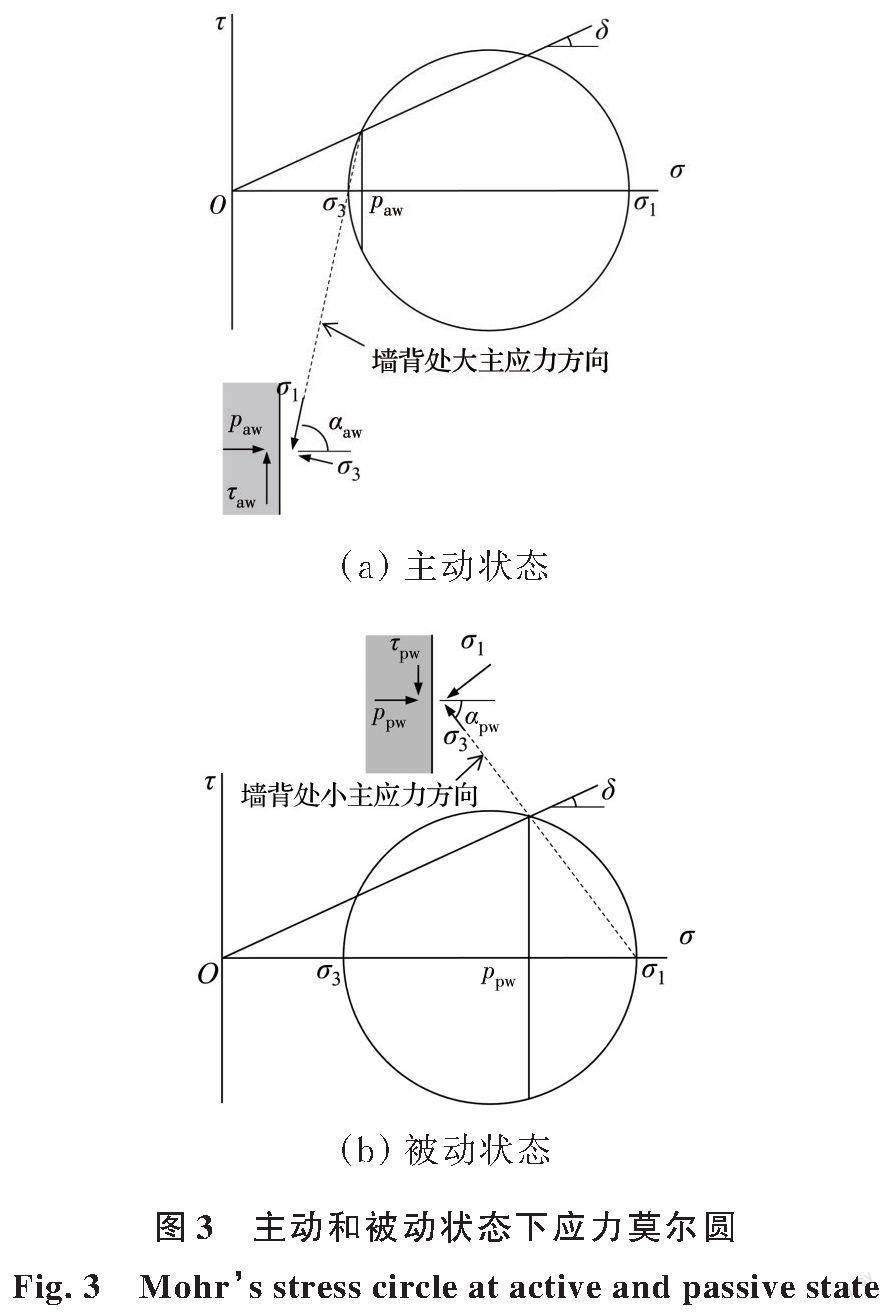
朗肯土壓力理論中假定主動(dòng)和被動(dòng)狀態(tài)下填土內(nèi)滑動(dòng)面的傾角θa、θp分別為π/4+φ/2、π/4-φ/2。圖2為主動(dòng)和被動(dòng)狀態(tài)下填土的小主應(yīng)力軌跡線。為便于計(jì)算，Paik等[16]將小主應(yīng)力軌跡假定為圓弧形。筆者將小主應(yīng)力軌跡和大主應(yīng)力軌跡均假定為圓弧形。圖3為主動(dòng)和被動(dòng)狀態(tài)下墻背上和填土內(nèi)滑動(dòng)面上任意一點(diǎn)土體的應(yīng)力莫爾圓。

可求出主動(dòng)狀態(tài)下兩處土體對(duì)應(yīng)的主應(yīng)力偏轉(zhuǎn)角αaw和αas為

被動(dòng)狀態(tài)下的主應(yīng)力偏轉(zhuǎn)角αpw和αps為

主動(dòng)狀態(tài)下微單元體在墻背處的側(cè)向應(yīng)力paw和微單元中任意點(diǎn)的垂直向應(yīng)力paz表示為

式中：αa為主動(dòng)狀態(tài)下該點(diǎn)的主應(yīng)力偏轉(zhuǎn)角。

被動(dòng)狀態(tài)下微單元體在墻背處側(cè)向應(yīng)力ppw和微單元任意點(diǎn)的垂直向應(yīng)力ppz可表示為

式中：αp為該點(diǎn)在被動(dòng)狀態(tài)下的主應(yīng)力偏轉(zhuǎn)角。

根據(jù)圖2的幾何關(guān)系可求得小主應(yīng)力軌跡線半徑ra和大主應(yīng)力軌跡線半徑rp。

式中：Ba和Bp分別為主動(dòng)和被動(dòng)狀態(tài)下?lián)跬翂εc填土內(nèi)滑動(dòng)面之間土體微分單元的寬度。將作用于微單元體的垂直方向的合力除以微單元體的寬度，

微單元體在擋土墻上的側(cè)向應(yīng)力除以微單元體的垂直應(yīng)力平均值即為側(cè)向應(yīng)力比[17]，則側(cè)向主動(dòng)應(yīng)力比Ka和側(cè)向被動(dòng)應(yīng)力比Kp為

根據(jù)作用在水平微單元片上的應(yīng)力平衡條件可得出

其中

C = tan θa （tan θa + tan δw ） （21）

D = tan θp （tan θp - tan δw ） （22）

不考慮填土表面荷載的情況下，邊界條件為paz│z=0=ppz│z=0=0。則可求出

擋土墻上任意一點(diǎn)主動(dòng)土壓力系數(shù)ka和被動(dòng)土壓力系數(shù)kp為

3 迭代法的引入

在擋土墻與填土之間設(shè)置EPS墊層后，EPS的壓縮是一個(gè)逐漸變化的過(guò)程。在這一過(guò)程中擋土墻的土壓力p隨著EPS壓縮量s的增大而減小，直至p和s的值穩(wěn)定。假定EPS為理想線彈性，將這一過(guò)程分為n步、每一步分為兩個(gè)獨(dú)立求解的部分：1）EPS受到一個(gè)已知的土壓力發(fā)生彈性變形產(chǎn)生一個(gè)壓縮量，在這一部分的求解過(guò)程中該已知的土壓力保持不變；2）通過(guò)式（1）可求得在該壓縮量下的土壓力，在這一部分的求解過(guò)程中該壓縮量保持不變，得出的土壓力將作為下一步中已知的土壓力。然后，引入迭代法，計(jì)算每一步中EPS的壓縮量和作用于擋土墻的土壓力，具體計(jì)算步驟如下。

初始狀態(tài)：EPS未發(fā)生變形，即s0=0，擋土墻受到的土壓力為靜止土壓力p0。

p0 = k0 γz （27）

第1步：EPS在p0的作用下產(chǎn)生壓縮量s1，進(jìn)而求得在s1的位移下?lián)跬翂λ艿降耐翂毫（s1）。

第n步：EPS在p（sn-1）的作用下產(chǎn)生壓縮量sn，進(jìn)而求得在sn的位移下?lián)跬翂λ艿降耐翂毫（sn）。

當(dāng)p（sn）約等于p（sn-1）時(shí)，停止迭代，sn和p（sn）分別為EPS的最終壓縮量和設(shè)置EPS后擋土墻的最終土壓力。需要注意的是，上述計(jì)算過(guò)程中，需用土與EPS之間的界面摩擦角δE代替土與擋土墻之間的界面摩擦角δw。

4 計(jì)算結(jié)果驗(yàn)證及分析

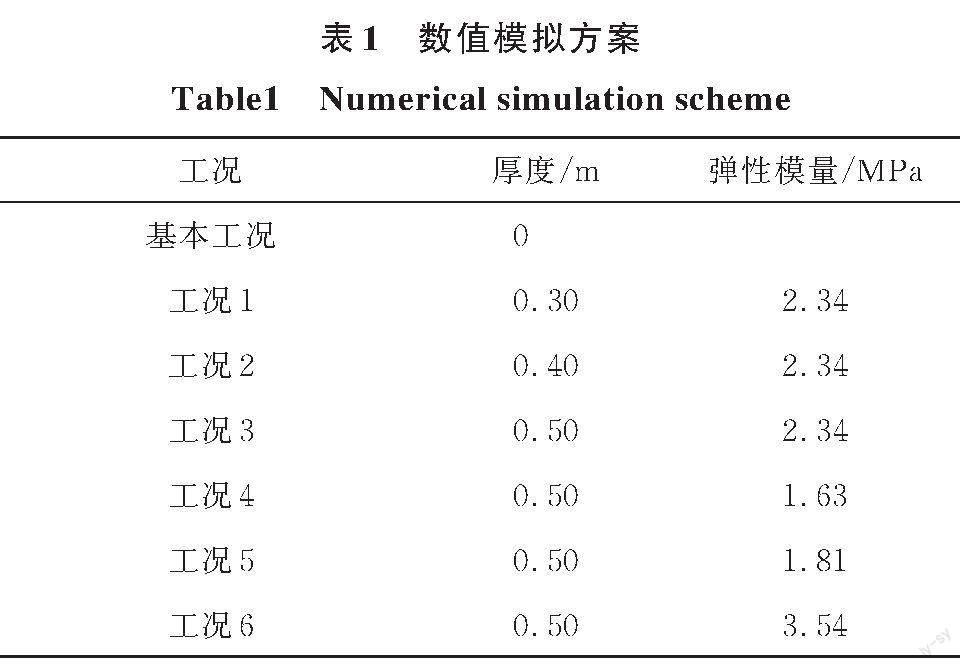
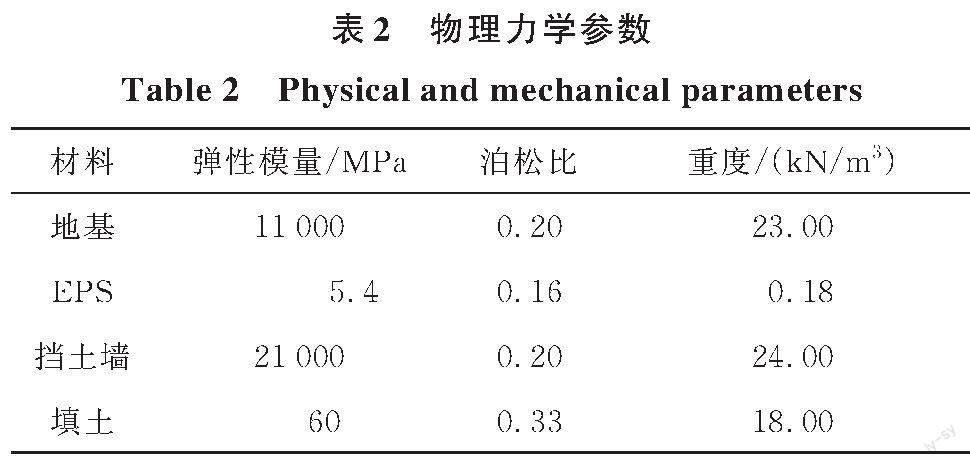
目前，EPS減載擋土墻土壓力在實(shí)際工程中的應(yīng)用較少，缺乏現(xiàn)場(chǎng)試驗(yàn)數(shù)據(jù)。既有研究大多為室內(nèi)縮尺試驗(yàn)研究，受限于擋土墻的高度，所得到的土壓力遠(yuǎn)小于實(shí)際工程中擋土墻所受到的土壓力。而EPS的減載效果隨著作用于擋土墻的土壓力的減小而減小，這將導(dǎo)致室內(nèi)縮尺試驗(yàn)不能如實(shí)反映EPS的減載效果。因此，筆者采用有限差分?jǐn)?shù)值軟件FLAC3D建立與實(shí)際工程中相符合的擋土墻模型（圖3），對(duì)所提出計(jì)算方法的合理性進(jìn)行驗(yàn)證。以EPS厚度和彈性模量為變量建立多個(gè)數(shù)值模型。各模型中EPS的彈性模量參考文獻(xiàn)[18]取值，且EPS墊層橫斷面尺寸均與擋土墻一致。此外，為驗(yàn)證數(shù)值模擬的準(zhǔn)確性，建立墻后未設(shè)置EPS板的工況，以便于模擬結(jié)果與Jaky靜止土壓力進(jìn)行對(duì)比。數(shù)值模擬方案見(jiàn)表1。

填土為砂土，采用Mohr-Coulomb模型，黏聚力c =0 kPa，內(nèi)摩擦角φ=32°。擋土墻為剛性擋土墻，墻高H為5 m，完全限制其側(cè)向位移。地基采用線彈性模型，并取較大的彈性模量值，以減弱地基土沉降對(duì)填土應(yīng)力狀態(tài)的影響。填土與擋土墻之間（墻后未設(shè)置EPS板的工況）以及填土與EPS板之間（墻后設(shè)置EPS板的工況）均設(shè)置接觸面，接觸面摩擦角分別為φ/2和φ/3[12]。數(shù)值模型中各材料的參數(shù)取值見(jiàn)表2。

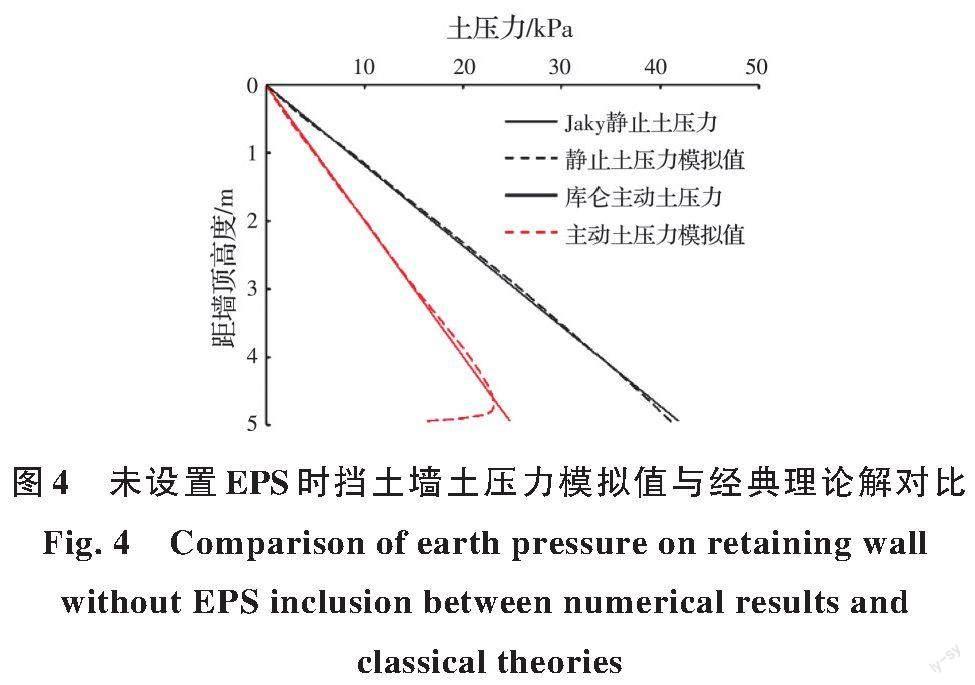
圖4為未設(shè)置EPS時(shí)（基本工況）的靜止和主動(dòng)模擬值與Jaky靜止土壓力和庫(kù)侖主動(dòng)土壓力理論解的對(duì)比。靜止土壓力的理論解與數(shù)值解能夠吻合；主動(dòng)土壓力的理論解與數(shù)值解在0～4.5 m范圍內(nèi)也能吻合，但在擋土墻底部位置的數(shù)值解明顯小于理論解。這是由于，為減小地基土沉降對(duì)土壓力的影響，數(shù)值模型中地基土彈性模量的取值遠(yuǎn)大于墻后填土。當(dāng)墻后填土產(chǎn)生位移的過(guò)程中，填土與地基土之間存在一定的邊界摩擦效應(yīng)，從而會(huì)導(dǎo)致土壓力模擬值的減小[8]。綜上，不考慮邊界效應(yīng)的情況下，數(shù)值模型具有較好的準(zhǔn)確性。

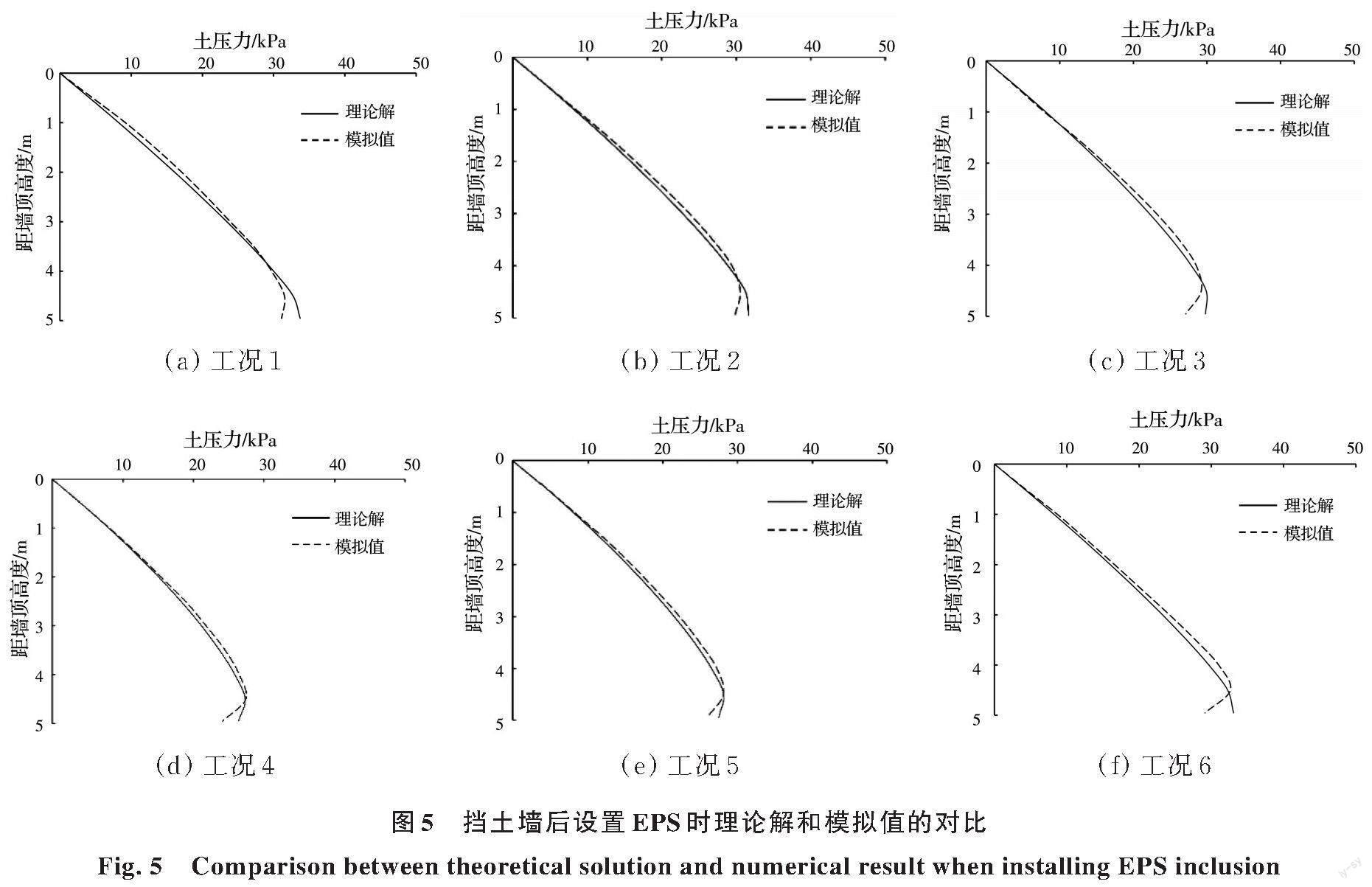
圖5對(duì)比了設(shè)置EPS后各工況的土壓力數(shù)值解與理論解（式（29）迭代計(jì)算的結(jié)果）。可以看出，在距墻頂高度0～4 m范圍內(nèi)模擬值略大于理論解。土壓力迭代計(jì)算中任意點(diǎn)的EPS壓縮量均按照離散點(diǎn)受壓的彈性變形計(jì)算，盡管EPS材料的泊松比較小，但EPS墊層受壓方向面積較大，各點(diǎn)的彈性變形并非都發(fā)生在一維應(yīng)力狀態(tài)下，可能導(dǎo)致EPS墊層壓縮量的模擬值略小于理論值，從而使土壓力的模擬值略大于理論解。同樣受數(shù)值模型邊界條件的影響，在擋土墻底部位置各工況的模擬值均明顯小于理論解。因此，忽略邊界條件的影響，提出的理論解總體上與數(shù)值解能較好地吻合，驗(yàn)證了提出方法的合理性。

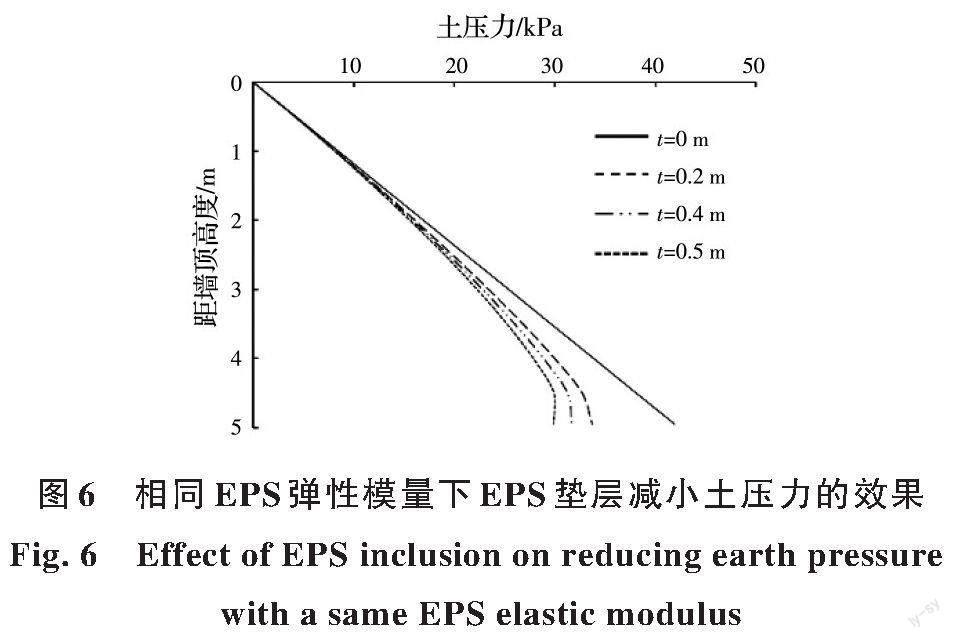
圖6、圖7對(duì)比了設(shè)置EPS后各工況的土壓力減小效果。隨著距墻頂高度的增加，各工況的土壓力減小效果均越來(lái)越明顯。對(duì)比工況1～工況3，即在EPS彈性模量不變的情況下（E=2.34 MPa），EPS減小土壓力的效果隨著EPS的厚度的增加而增強(qiáng)；對(duì)比工況3～工況6，在EPS厚度一定的情況下（t=0.5 m），EPS減小土壓力的效果隨著EPS的彈性模量的增加而減弱。EPS的彈性模量隨著其密度的減小而減小，但當(dāng)采用低密度的EPS時(shí)，其屈服強(qiáng)度也較低，若擋土墻土壓力值較大，會(huì)導(dǎo)致EPS處于屈服或非線性硬化階段。同時(shí)，EPS厚度若過(guò)大，將會(huì)導(dǎo)致緊鄰擋土墻區(qū)域路面出現(xiàn)不均勻沉降。因此，在實(shí)際工程中，需綜合考慮EPS的設(shè)計(jì)參數(shù)和減載效果，避免為追求減載效果而導(dǎo)致工程隱患。

5 結(jié)論

1）將EPS墊層的壓縮量視為墻后填土的位移量，推導(dǎo)了考慮土拱效應(yīng)的擋土墻主動(dòng)和被動(dòng)土壓力系數(shù)解析解，將其代入擋土墻土壓力-位移的關(guān)系方程，并引入迭代法進(jìn)行收斂計(jì)算，解決了設(shè)計(jì)階段EPS實(shí)際壓縮量未知這一關(guān)鍵問(wèn)題，最終得出設(shè)置EPS墊層的擋土墻土壓力解析解。

2）建立一系列有限差分?jǐn)?shù)值模型，得到的模擬值與理論解總體上能較好地吻合，驗(yàn)證了提出方法的合理性。

3）在EPS彈性模量不變的情況下，EPS減小土壓力的效果隨著EPS的厚度的增加而增強(qiáng)；而在EPS厚度一定的情況下，隨著EPS的彈性模量的增加，EPS減小土壓力的效果逐漸減弱。

參考文獻(xiàn)

[1]? HORVATH J S. The compressible inclusion function of EPS geofoam [J]. Geotextiles and Geomembranes， 1997， 15（1/2/3）： 77-120.

[2]? BATHURST R J， ZARNANI S， GASKIN A. Shaking table testing of geofoam seismic buffers [J]. Soil Dynamics and Earthquake Engineering， 2007， 27（4）： 324-332.

[3]? BATHURST R J， ZARNANI S. Earthquake load attenuation using EPS geofoam buffers in rigid wall applications [J]. Indian Geotechnical Journal， 2013， 43（4）： 283-291.

[4]? IKIZLER S B， AYTEKIN M， NAS E. Laboratory study of expanded polystyrene （EPS） geofoam used with expansive soils [J]. Geotextiles and Geomembranes， 2008， 26（2）： 189-195.

[5]? ERTUGRUL O L， TRANDAFIR A C. Reduction of lateral earth forces acting on rigid nonyielding retaining walls by EPS geofoam inclusions [J]. Journal of Materials in Civil Engineering， 2011， 23（12）： 1711-1718.

[6]? ERTUGRUL O L， TRANDAFIR A C. Lateral earth pressures on flexible cantilever retaining walls with deformable geofoam inclusions [J]. Engineering Geology， 2013， 158： 23-33.

[7]? NI P P， MEI G X， ZHAO Y L. Displacement-dependent earth pressures on rigid retaining walls with compressible geofoam inclusions： Physical modeling and analytical solutions [J]. International Journal of Geomechanics， 2017， 17（6）： 04016132.

[8]? KIM H， WITTHOEFT A F， KIM D. Numerical study of earth pressure reduction on rigid walls using EPS geofoam inclusions [J]. Geosynthetics International， 2018， 25（2）： 180-199.

[9]? 鄭俊杰， 景丹， 謝明星， 等. 剛性擋土墻后設(shè)置EPS墊層的設(shè)計(jì)方法研究[J]. 華中科技大學(xué)學(xué)報(bào)（自然科學(xué)版）， 2020， 48（12）： 96-101.

ZHENG J J， JING D， XIE M X， et al. Study on design scheme of installing EPS cushion behind the rigid retaining wall[J]. Journal of Huazhong University of Science and Technology （Natural Science Edition）， 2020， 48（12）： 96-101. （in Chinese）

[10]? 鄭俊杰， 邵安迪， 謝明星， 等. 擋土墻后EPS板減壓性能模型試驗(yàn)研究[J]. 土木與環(huán)境工程學(xué)報(bào)（中英文）， 2020， 42（4）： 1-9.

ZHENG J J， SHAO A D， XIE M X， et al. Model test study on decompression performance of EPS boards behind retaining walls [J]. Journal of Civil and Environmental Engineering， 2020， 42（4）： 1-9. （in Chinese）

[11]? 鄭俊杰， 邵安迪， 謝明星， 等. 不同填土寬度下設(shè)置EPS墊層擋土墻試驗(yàn)研究[J]. 巖土力學(xué)， 2021， 42（2）： 324-332.

ZHENG J J， SHAO A D， XIE M X， et al. Experimental study on retaining wall with EPS cushion under different backfill widths [J]. Rock and Soil Mechanics， 2021， 42（2）： 324-332. （in Chinese）

[12]? 謝明星， 鄭俊杰， 邵安迪， 等. 設(shè)置EPS柔性墊層的剛性擋土墻土壓力研究[J]. 巖土工程學(xué)報(bào)， 2019， 41（Sup1）： 65-68.

XIE M X， ZHENG J J， SHAO A D， et al. Lateral earth pressure on rigid retaining walls with EPS deformable geofoam inclusions [J]. Chinese Journal of Geotechnical Engineering， 2019， 41（Sup1）： 65-68. （in Chinese）

[13]? 許曉亮， 王鑫佩， 曾林風(fēng)， 等. 含EPS墊層及輕量填土擋墻的墻后土壓力及其減載效應(yīng)[J/OL]. 土木與環(huán)境工程學(xué)報(bào)（中英文）. http：//kns.cnki.net/kcms/detail/50.1218.TU.20221202.1110.001.html.

XU X L， WANG X P， ZENG L F， et al. Lateral earth pressure and load-reducing effect behind retaining wall with EPS cushion and light-weight soil [J/OL]. Journal of Civil and Environmental Engineering. http：//kns.cnki.net/kcms/detail/50.1218.TU.20221202.1110.001.html.（in Chinese）

[14]? MEI G X， CHEN Q M， SONG L H. Model for predicting displacement-dependent lateral earth pressure[J]. Canadian Geotechnical Journal， 2009， 46（8）： 969-975.

[15]? JAKY J. The coefficient of earth pressure at rest [J]. Journal of the Society of Hungarian Architects and Engineers， 1944： 355-358.

[16]? PAIK K H， SALGADO R. Estimation of active earth pressure against rigid retaining walls considering arching effects [J]. Géotechnique， 2003， 53（7）： 643-653.

[17]? HANDY R L. The arch in soil arching [J]. Journal of Geotechnical Engineering， 1985， 111（3）： 302-318.

[18]? XIE M X， ZHENG J J， SHAO A D， et al. Study of lateral earth pressures on nonyielding retaining walls with deformable geofoam inclusions [J]. Geotextiles and Geomembranes， 2020， 48（5）： 684-690.