某水電站2號變形體傾倒變形影響因素研究

朱存金，汪 惠，沈 飛，羅 林，唐 娟

(1.四川省地質工程勘察院集團有限公司，四川 成都 610032；2.四川省天晟源環保股份有限公司，四川 成都 610037)

0 引 言

傾倒變形是指反傾層狀巖質邊坡表部巖層因蠕動變形而向臨空方向一側發生彎曲、折斷，形成所謂“點頭哈腰”的現象[1]。Goodman和Bray等對層狀邊坡的傾倒變形現象進行了系統研究[2]，引起了巖土工程界的廣泛關注。Hoek和Bray在巖石邊坡變形破壞類型中將傾倒破壞單獨列為一類[3]。近年來，許多國內外重大工程中出現了大量與傾倒變形相關的工程地質問題，如金川露天礦上盤西區邊坡[4]、錦屏一級水電站左岸高邊坡[5]、小灣水電站飲水溝邊坡[6]、湯屯高速公路Ⅲ-4號高邊坡[7]等，均出現了傾倒變形現象。這些傾倒變形，不僅延誤了長時間的工期，而且增加了巨大的工程投資。

隨著社會經濟的發展和科學技術的進步，越來越多的國內外學者和工程技術人員對傾倒變形影響因素進行了研究[8-22]。韓貝傳等[8]研究了結構面間距及力學參數對傾倒變形的影響。蘇立海[9]分析了傾角、坡角、層厚、巖體強度以及軟弱夾層等因素對傾倒變形的影響規律。Nichol[10]分析了節理連通率、巖石強度、坡腳開挖條件等因素對傾倒變形的影響。Brideau等[11]研究了斷續節理傾向對傾倒變形的影響。程東幸等[12]以廣西龍灘水電站邊坡為例，通過正交方法設計數值模擬試驗，研究了邊坡的結構、巖體參數、層面參數、地應力等因素對傾倒變形的影響，并且提出了優勢傾角范圍。王宇等[13]分析了巖層厚度、巖層傾角、地震作用、地下水作用等因素對傾倒變形的影響。Xie等[14]分析了相鄰巖層厚度差異大小對傾倒變形的影響。王立偉等[15]以某水電站反傾層狀巖質邊坡為例，對傾倒變形的影響因素分析表明，巖層傾角、風化程度、水平地應力、地下水及地震作用是主要影響因素，邊坡坡角和巖層厚度是次要影響因素，邊坡坡角為70°左右、巖層傾角為65°左右是傾倒破壞的優勢角。

鑒于目前國內外學者的相關研究中，系統全面地對比計算各影響因子敏感性的研究相對較少，本文采用離散單元法，通過單因素試驗研究了邊坡幾何特征參數、巖體物理力學參數、層面力學參數等因素，對某水電站2號傾倒變形體的影響規律，并在此基礎上通過正交試驗及灰色關聯法進行了影響因子敏感性分析。

1 計算模型及參數

根據2號變形體實際地質條件及工程地質剖面圖加以適當概化建模，建模時坡面未考慮實際削坡中馬道的設置。計算模型左右邊界固定水平向位移，下邊界固定垂直向位移，上邊界為自由邊界，只考慮自重應力場。采用UDEC中庫侖滑動模型模擬層面的行為，巖體按M-C彈塑性模型考慮。反傾巖質邊坡傾倒變形程度評價指標中，目前大多數學者均采用坡頂位移為評價指標[23]，因此本文在影響因素分析過程中選擇各個模型對應同一點(A點)的水平向位移進行對比分析。計算模型見圖1。圖中，t為巖層厚度；α為坡角；β為巖層傾角。巖體和層面的物理力學參數分別見表1、2。

表1 巖體物理力學參數取值

表2 層面力學參數取值

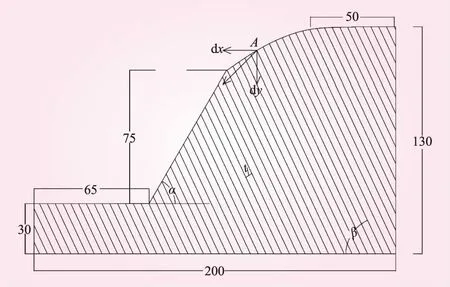
圖1 影響因素分析模型(單位：m)

2 基于單因素試驗的各因素對傾倒變形的影響

為全面確定各個影響因素對2號變形體傾倒變形的影響規律，選取邊坡幾何特征參數、巖體物理力學參數、層面力學參數作為一級影響因子，并分別對應細分出二級影響因子，建立該變形體傾倒變形因子評價體系。在此基礎上，基于單因素變量法，分別從邊坡幾何特征參數(巖層坡角、層厚、傾角)、巖體物理力學參數(彈性模量、泊松比、內摩擦角、黏聚力、抗拉強度、容重)、層面力學參數(內摩擦角、黏聚力、剛度比)等因素擬定方案，采用離散元程序UDEC研究各影響因子對2號變形體傾倒變形的影響規律。

2.1 邊坡幾何特征參數

2.1.1 巖層坡角

一般認為，邊坡坡度越大則邊坡相對越不穩定，坡度越小則相對越穩定，這說明坡角對邊坡穩定性起著重要的影響作用。數值模擬試驗中，固定其他因素不變，邊坡坡角分別為35°、45°、55°、65°、75°、85°進行計算，對邊坡各模型同一點的位移監測值進行分析。不同坡角邊坡坡頂位移變化見圖2。

圖2 邊坡坡頂位移隨坡角的變化規律

從圖2可知，在坡角小于45°時，監測點的水平向位移較小，邊坡不易發生傾倒變形；坡角在55°～85°之間，邊坡傾倒變形明顯，且總體上水平向位移隨著坡度的增大呈逐漸增大趨勢，尤其坡角在55°～65°之間，隨著坡角的增大水平向位移急劇增加，65°之后位移值變化不大；當坡角為75°時，坡頂水平位移達到最大值；坡角超過75°以后邊坡傾倒變形程度減弱。監測點的垂直向位移變化規律與水平向大致一致，但其值相對較小。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。因此，2號變形體傾倒變形程度隨著坡角的增大逐漸增強，55°～85°坡角最有利于邊坡發生傾倒變形，75°時傾倒變形程度最大。

2.1.2 巖層傾角

一般認為，在重力作用的影響下，反傾層狀巖質邊坡巖層傾角越陡，自重在垂直向的分力相應較大，則邊坡更容易發生彎曲變形，這說明巖層傾角對傾倒變形程度起著重要的影響。數值模擬試驗中，固定其他因素不變，巖層傾角分別為25°、35°、45°、55°、65°、75°、85°進行計算，對邊坡各模型同一點的位移監測值進行分析。不同傾角邊坡坡頂位移變化見圖3。

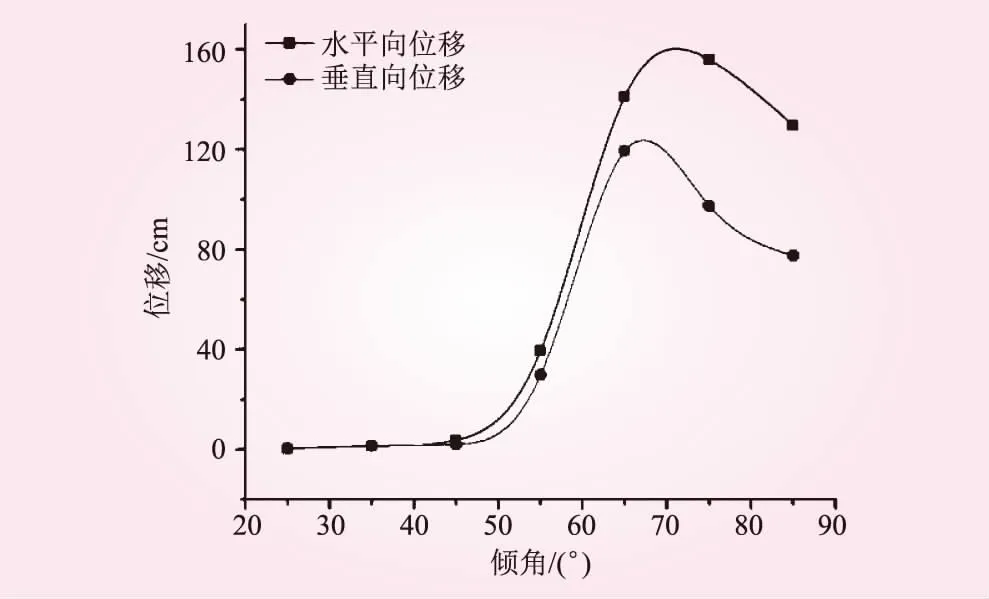
圖3 邊坡坡頂位移隨傾角的變化規律

從圖3可知，在巖層傾角小于45°時，監測點的水平向位移較小，邊坡不易發生傾倒變形；傾角在65°～85°之間，邊坡傾倒變形明顯，且總體上水平向位移隨著傾角的增大呈逐漸增大趨勢，尤其傾角在55°～65°之間，隨著傾角的增大水平向位移急劇增加，65°之后位移值變化不大；當傾角為75°時坡頂水平位移達到最大值；傾角超過75°以后邊坡傾倒變形程度稍有減弱。監測點的垂直向位移變化規律與水平向大致一致，但其值相對較小。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。因此，2號變形體傾倒變形程度隨著巖層傾角的增大逐漸增強，55°～85°傾角最有利于邊坡發生傾倒變形，75°時傾倒變形程度最大。

2.1.3 巖層層厚

巖層層厚越厚，巖體剛度越大。一般認為，越厚的巖層越不容易發生傾倒變形。數值模擬試驗中，固定其他因素不變，巖層層厚分別為1、2、3、4 m和5 m進行計算，對邊坡各模型同一點的位移監測值進行分析。不同層厚邊坡坡頂位移變化見圖4。

從圖4可知，層厚在1～3 m之間，水平向位移隨著層厚的增大逐漸增大，4 m之后呈逐漸減小趨勢。這主要是由于層厚小于3 m時，隨著巖層層厚的增大雖然剛度增大但單層重力變大，剛度的影響小于重力的影響，故水平向位移隨著層厚的增大逐漸增大；當層厚大于3 m時，隨著巖層層厚的增大，剛度的影響大于重力的影響，故水平向位移隨著層厚的增大呈逐漸減小趨勢。監測點的垂直向位移變化規律與水平向大致一致，但其值相對較小。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。因此，當層厚在一定范圍內，2號變形體傾倒變形程度隨著層厚的增大逐漸增大；當層厚超過一定值時，邊坡傾倒變形程度隨著層厚的增大逐漸減小。

2.2 巖體物理力學參數

2.2.1 彈性模量

固定其他因素不變，彈性模量分別為1、2、3、5 GPa和7 GPa進行計算，對邊坡各模型同一點的位移監測值進行分析。不同彈性模量邊坡坡頂位移變化見圖5。

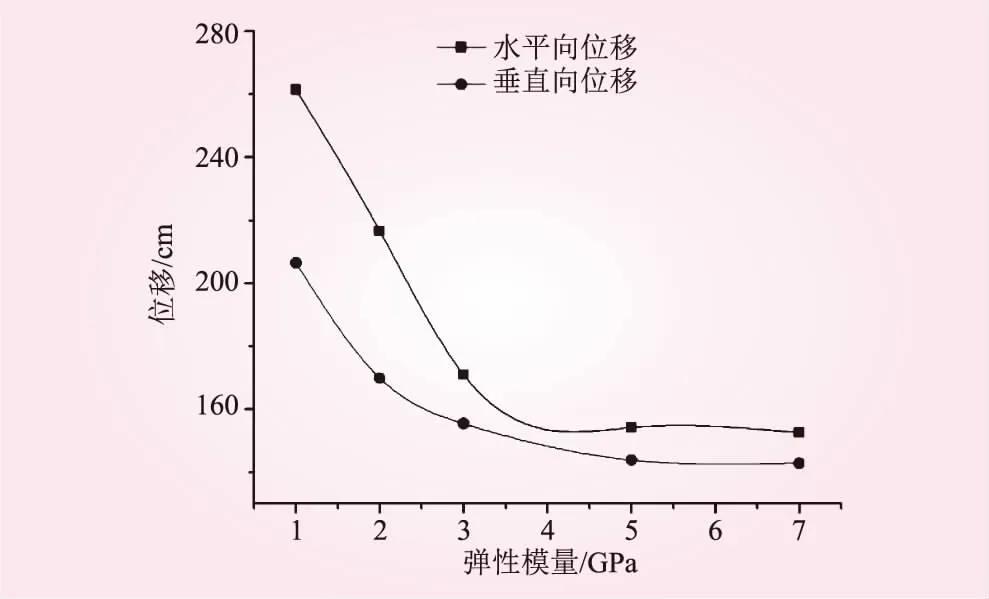
圖5 邊坡坡頂位移隨巖體彈性模量的變化規律

從圖5可知，彈性模量在1～3 GPa之間，邊坡傾倒變形明顯，且水平向位移隨著彈性模量的增大呈逐漸減小趨勢；5 GPa之后位移變化不大，趨于平緩。監測點的垂直向位移變化規律與水平向大致一致，但其值相對較小。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。整體上，2號變形體傾倒變形程度隨著彈性模量的增大逐漸減小，當彈性模量超過一定值時，隨著彈性模量的增加傾倒變形程度變化不明顯。

2.2.2 泊松比

固定其他因素不變，泊松比分別為0.24、0.27、0.3、0.33、0.36進行計算，對邊坡各模型同一點的位移監測值進行分析。不同泊松比邊坡坡頂位移變化見圖6。

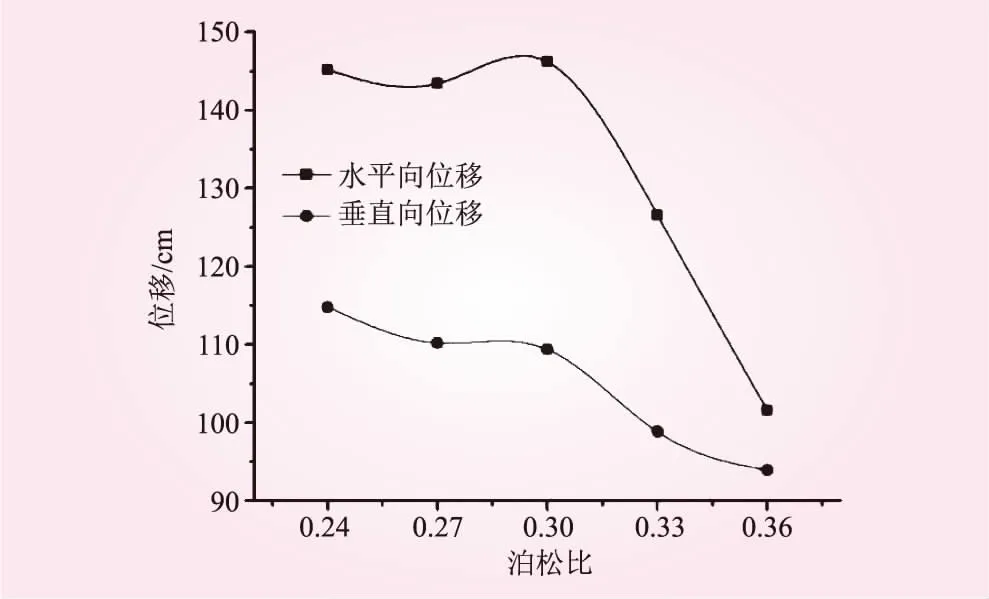
圖6 邊坡坡頂位移隨巖體泊松比的變化規律

從圖6可知，泊松比在0.24～0.3之間，水平向位移變化不大；泊松比大于0.33時，邊坡傾倒變形程度稍有減弱。監測點的垂直向位移變化規律與水平向大致一致，但其值相對較小。整體上，隨著泊松比的變化，2號變形體傾倒變形程度變化不明顯，當泊松比超過一定值時，隨著泊松比的增加，傾倒變形程度稍有減弱。

2.2.3 黏聚力

固定其他因素不變，巖體黏聚力分別為0.3、0.4、0.5、0.6 MPa和0.7 MPa進行計算，對邊坡各模型同一點的位移監測值進行分析。不同巖體黏聚力邊坡坡頂位移變化見圖7。

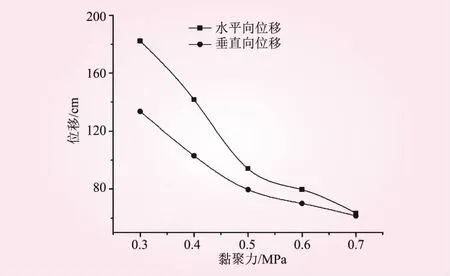
圖7 邊坡坡頂位移隨巖體黏聚力的變化規律

從圖7可知，黏聚力在0.3～0.7 MPa之間，水平向位移隨著黏聚力的增大呈逐漸減小趨勢。監測點的垂直向位移變化規律與水平向大致一致，但其值相對較小。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。因此，2號變形體傾倒變形程度隨著黏聚力的增大逐漸減弱。

2.2.4 內摩擦角

固定其他因素不變，巖體內摩擦角分別為30°、33°、36°、39°、42°進行計算，對邊坡各模型同一點的位移監測值進行分析。不同巖體內摩擦角邊坡坡頂位移變化見圖8。

圖8 邊坡坡頂位移隨巖體內摩擦角的變化規律

從圖8可知，巖體內摩擦角在30°～42°之間，監測點的水平向位移變化不大。監測點的垂直向位移變化規律與水平向大致一致。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。整體上，隨著內摩擦角的變化，2號變形體傾倒變形程度變化不明顯。

2.2.5 抗拉強度

固定其他因素不變，抗拉強度分別為2、4、6、8 MPa和10 MPa進行計算，對邊坡各模型同一點的位移監測值進行分析。不同抗拉強度邊坡坡頂位移變化見圖9。

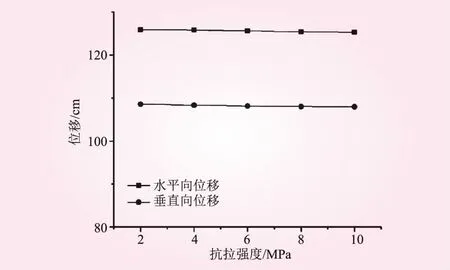
圖9 邊坡坡頂位移隨巖體抗拉強度的變化規律

從圖9可知，抗拉強度在2～10 MPa之間，監測點的水平向位移幾乎不變。監測點的垂直向位移變化規律與水平向大致一致。整體上，隨著抗拉強度的變化，2號變形體傾倒變形程度幾乎不變。

2.2.6 容重

固定其他因素不變，巖體容重分別為24、25、26、27 kN/m3和28 kN/m3進行計算，對邊坡各模型同一點的位移監測值進行分析。不同容重邊坡坡頂位移變化見圖10。

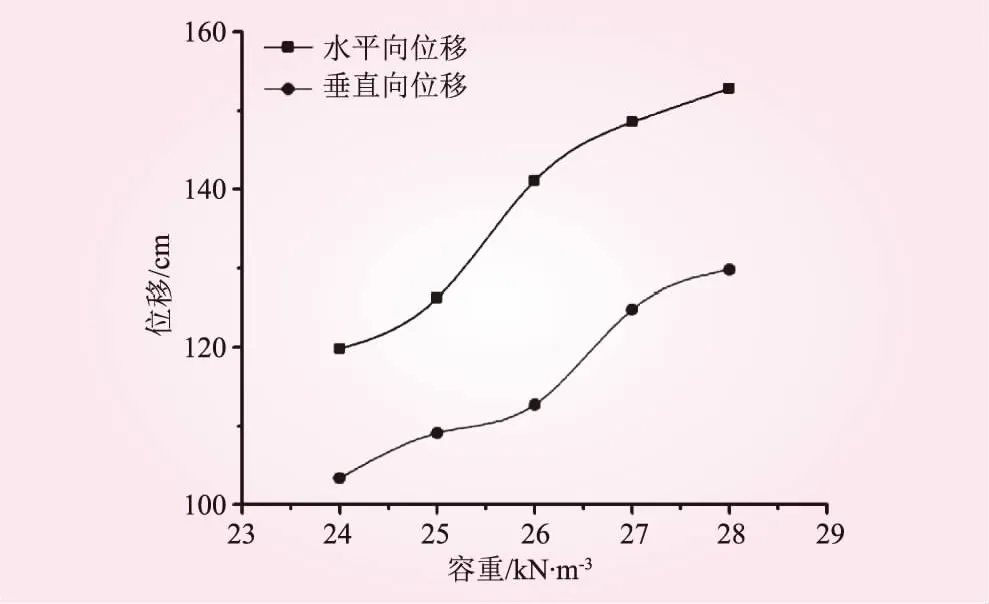
圖10 邊坡坡頂位移隨巖體容重的變化規律

從圖10可知，水平向位移隨著巖體容重的增大呈逐漸增大趨勢。監測點的垂直向位移變化規律與水平向一致，但其值相對較小。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。因此，2號變形體傾倒變形程度隨著巖體容重的增大逐漸增強。

2.3 層面力學參數的影響

2.3.1 黏聚力

固定其他因素不變，層面黏聚力分別為0.005、0.01、0.02、0.05 MPa和0.1 MPa進行計算，對邊坡各模型同一點的位移監測值進行分析。不同層面黏聚力邊坡坡頂位移變化見圖11。

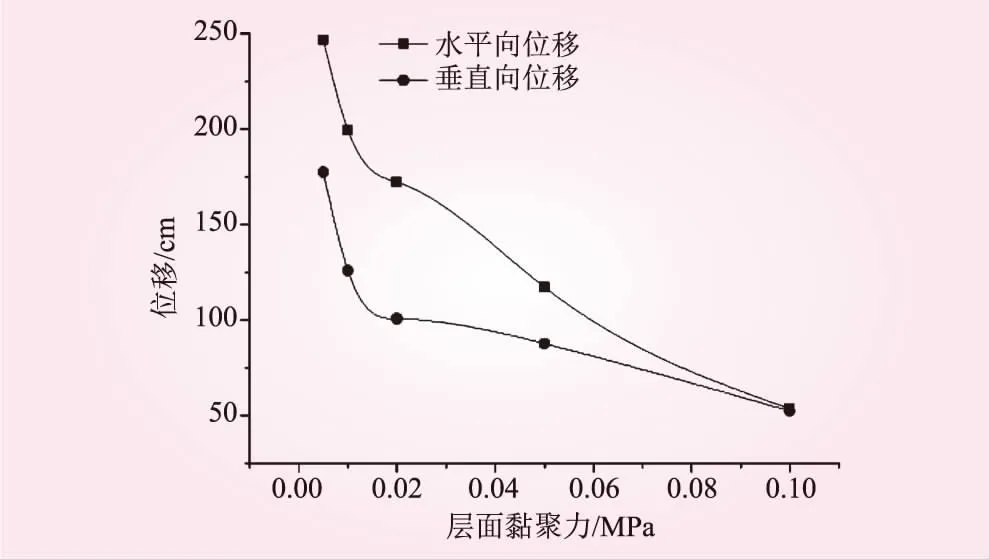
圖11 邊坡坡頂位移隨層面黏聚力的變化規律

從圖11可知，層面黏聚力在0 ～0.1 MPa之間，水平向位移隨著層面黏聚力的增大呈逐漸減小趨勢。監測點的垂直向位移變化規律與水平向大致一致，但其變化幅度相對較小。通過2個方向位移的比較，邊坡傾倒變形主要以水平向變形為主。因此，2號變形體傾倒變形程度隨著層面黏聚力的增大逐漸減弱。

2.3.2 內摩擦角

固定其他因素不變，層面內摩擦角分別為13°、16°、19°、22°和25°進行計算，對邊坡各模型同一點的位移監測值進行分析。不同層面傾角邊坡坡頂位移變化見圖12。

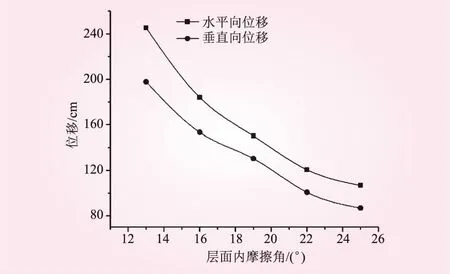
圖12 邊坡坡頂位移隨層面內摩擦角的變化規律

從圖12可知，層面內摩擦角在13°～25°之間，水平向位移隨著層面內摩擦角的增大呈逐漸減小趨勢。監測點的垂直向位移變化規律與水平向一致。因此，2號變形體傾倒變形程度隨著層面內摩擦角的增大逐漸減弱。

2.3.3 層面剛度比

層面剛度比為層面法向剛度與切向剛度的比值。固定其他因素不變，層面剛度比分別為1、3、5、7、9進行計算，對邊坡各模型同一點的位移監測值進行分析。不同層面剛度比邊坡坡頂位移變化見圖13。

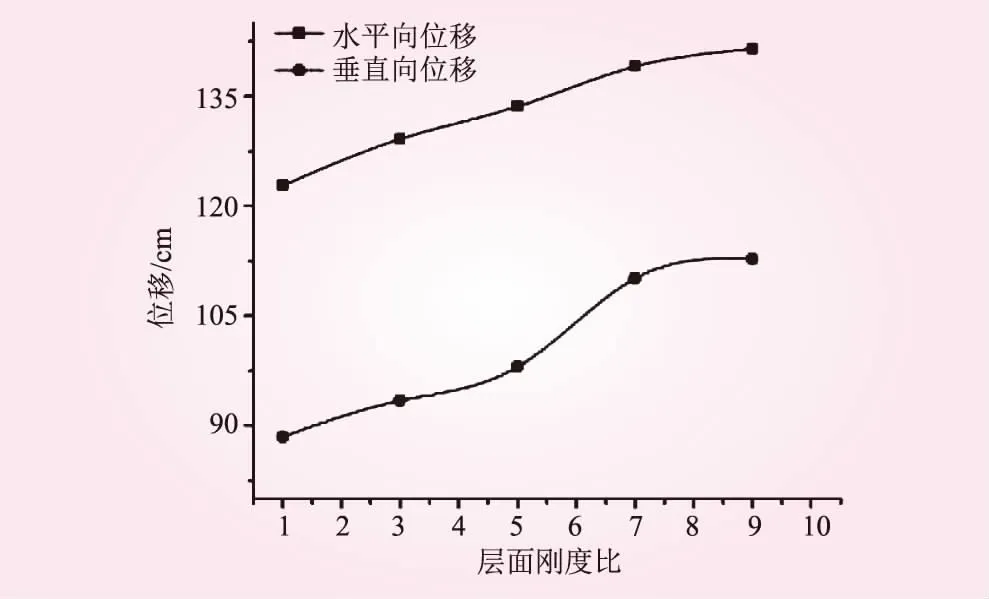
圖13 邊坡坡頂位移隨層面剛度比的變化規律

從圖13可知，層面剛度比在1～9之間，水平向位移隨著層面剛度比的增大稍有增大，但增加幅度很小。監測點的垂直向位移變化規律與水平向大致一致，但其值相對較小。因此，2號變形體傾倒變形程度隨著層面剛度比的增大呈微弱增長的趨勢。

3 基于正交試驗的影響因素敏感性分析

基于單因素變量法的研究結果可知，巖體泊松比、巖體抗拉強度、層面剛度比等因素對2號變形體傾倒變形影響相對較小，因此本次正交試驗選取的主要因素為層厚、傾角、坡角、巖體容重、彈性模量、巖體黏聚力、巖體內摩擦角、結構面黏聚力、結構面內摩擦角等9個因素。在上述9個因素中，每個因素的取值范圍按概化取為5個水平，確定正交表。采用 UDEC程序對2號變形體傾倒變形進行數值模擬，選擇各個模型對應坡頂同一點(A點)的水平向位移進行監測，模擬結果見表3。采用灰色關聯分析法[24]進行分析，步驟如下：

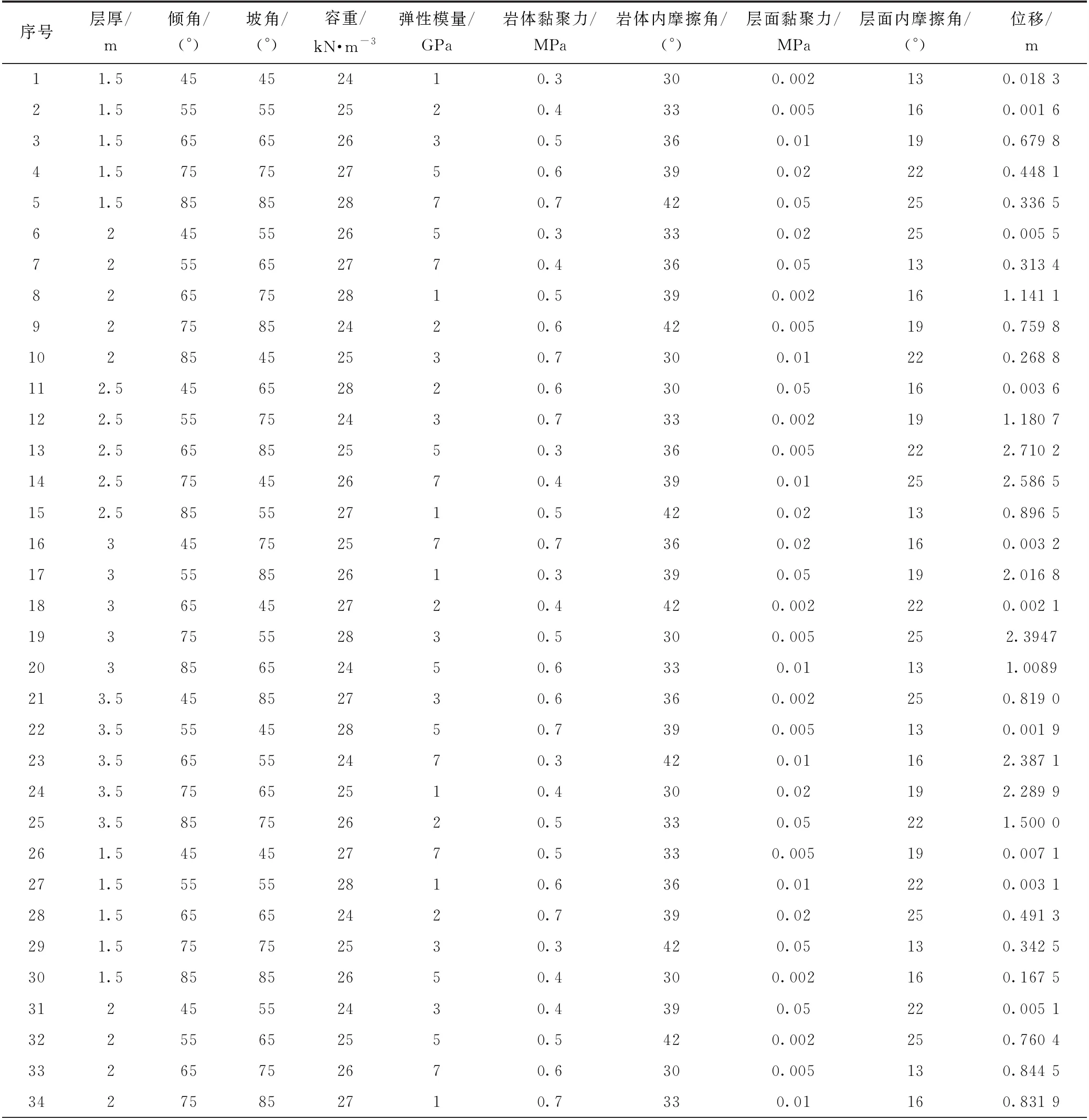
表3 正交試驗數值模擬結果

(1)確定分析數列。首先選取反映系統特征行為的母序列X0和子序列Xi。子序列即為影響系統行為特征的數據序列。

(2)對分析數列中的數據進行無量綱化處理。本文采用Z-score法處理，即

(1)

(3)求取母序列與各子序列的灰色關聯系數。計算母序列與各子序列差的絕對值，并取得最大差序列和最小差序列，即

(2)

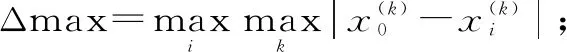
(3)

式中，ρ為分辨系數，一般在0～1之間，取0.5。

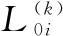
(4)

根據R0i大小得出關聯序的先后順序，關聯度在0～1，越接近1，則說明該因素對目標值影響最敏感；反之，越接近0，則該因素對目標值影響越不敏感。

(5)關聯度排序。根據所獲得的關聯度大小對影響因素進行排序，從而得出影響因素敏感性大小。

在表3正交設計試驗模擬結果的基礎上，采用基于灰色關聯理論編寫的MATLAB計算程序，得出各因素的關聯度，結果見表4。從表4可知，根據關聯度由大至小順序可得出，影響因素的主次依次為：層厚、傾角、坡角、彈性模量、層面內摩擦角、層面黏聚力、容重、巖體黏聚力、巖體內摩擦角。即影響2號變形體傾倒變形最為敏感的3個因素依次為層厚、傾角、坡角；彈性模量、層面內摩擦角、層面黏聚力敏感性次之；最不敏感的因素為容重、巖體黏聚力、巖體內摩擦角。

表4 各因素關聯度結果

在上述9個二級影響因子敏感性分析的基礎上，根據各二級因子的歸屬進行一級影響因子(邊坡幾何特征參數、巖體物理力學參數、層面力學參數)敏感性分析計算，公式如下

(5)

(6)

(7)

通過式(5)～(7)分別求得2號變形體傾倒變形一級影響因子關聯度R0i，邊坡幾何特征參數為0.711、巖體物理力學參數為0.660、層面力學參數為0.675。根據關聯度由大至小順序，在3個一級影響因子中，邊坡幾何特征參數最為敏感，巖體物理力學參數最不敏感，層面力學參數敏感性居中。

4 結 語

本文以某水電站2號變形體為研究對象，采用離散單元法，通過單因素試驗，研究了邊坡幾何特征參數、巖體物理力學參數、層面力學參數等因素對該變形體傾倒變形的影響規律，并在此基礎上通過正交試驗及灰色關聯度分析法進行了影響因素敏感性分析，得出以下結論：

(1)基于某水電站2號變形體單因素試驗的傾倒變形影響規律研究表明，2號變形體傾倒變形程度與容重成正相關關系；與彈性模量、巖體黏聚力、層面黏聚力、層面內摩擦角成負相關關系；隨坡角、傾角、層厚的增大，傾倒變形程度呈現先增大后減小的趨勢；隨泊松比、巖體內摩擦角、抗拉強度、層面剛度比的變化，傾倒變形程度變化不明顯。

(2)基于正交試驗設計及灰色關聯度分析的敏感性分析表明，影響2號變形體傾倒變形最為敏感的3個因素依次為層厚、傾角、坡角；彈性模量、層面內摩擦角、層面黏聚力敏感性次之；最不敏感的因素為容重、巖體黏聚力、巖體內摩擦角。

(3)在3個一級影響因子中，邊坡幾何特征參數最為敏感，巖體物理力學參數最不敏感，層面力學參數敏感性居中。

本文結果只是針對個體工程研究得出的，尚需要更多的工程案例研究，才能為反傾邊坡的機理研究提供可靠的依據。