基于RBF神經(jīng)網(wǎng)絡(luò)的自主水下航行器模型預(yù)測路徑跟蹤控制

郭琳鈺, 高劍, 焦慧鋒, 宋允軒, 陳依民, 潘光

(1.西北工業(yè)大學(xué) 航海學(xué)院, 陜西 西安 710072; 2.西北工業(yè)大學(xué) 無人系統(tǒng)技術(shù)研究院, 陜西 西安 710072;3.中國船舶科學(xué)研究中心, 江蘇 無錫 214082)

自主水下航行(AUV)因其航程遠(yuǎn)、作業(yè)精準(zhǔn)度高、可重復(fù)使用等特點(diǎn),成為了人類認(rèn)識和探索海洋領(lǐng)域必不可缺的工具,在近些年逐漸被廣泛應(yīng)用。精確路徑跟蹤控制是AUV實(shí)現(xiàn)自主航行的關(guān)鍵技術(shù)之一,受到國內(nèi)外學(xué)者的廣泛關(guān)注。

在路徑跟蹤控制問題上,早期的運(yùn)動控制方法為比例-積分-微分(PID)控制,文獻(xiàn)[1]使用PID控制器實(shí)現(xiàn)了路徑跟蹤,并通過大量的海上實(shí)驗(yàn)證明了該控制器的魯棒性和穩(wěn)定性。

水下航行器多為欠驅(qū)動、強(qiáng)耦合的非線性系統(tǒng),并受到未建模動態(tài)和環(huán)境擾動的影響。為提高水下航行器運(yùn)動控制面對多種不確定因素的魯棒性,研究人員提出了基于自適應(yīng)控制[2-4]、滑模控制[5-6]、反步控制[7-8]、神經(jīng)網(wǎng)絡(luò)控制[9-10]等路徑跟蹤控制方案。

Gao等[11]研究了水平面AUV非線性路徑跟蹤控制問題。以路徑上自由參考點(diǎn)為起點(diǎn)的Serret-Frenet坐標(biāo)來描述路徑跟蹤誤差及其動態(tài)方程,解決了經(jīng)典方法中的奇異性問題。Sun等[12]基于改進(jìn)的反步法和滑模控制原理,研究了考慮未知環(huán)境干擾下的欠驅(qū)動水下航行器的路徑跟蹤控制問題。通過數(shù)值仿真驗(yàn)證了濾波反步滑模控制器的控制效果。與傳統(tǒng)的反步滑模控制器相比,控制器輸出的抖振明顯減小,跟蹤誤差收斂更快,達(dá)到穩(wěn)定跟蹤狀態(tài)所需的時間更短,穩(wěn)定性更高。然而,AUV水下作業(yè)環(huán)境復(fù)雜,需要考慮各種約束條件,上述控制器難以處理約束問題。

模型預(yù)測控制(MPC)是一種基于模型的閉環(huán)優(yōu)化控制策略,相對于傳統(tǒng)控制方法的優(yōu)勢在于能夠在控制器設(shè)計(jì)范圍內(nèi)系統(tǒng)地處理帶約束條件的多輸入多輸出問題,目前己經(jīng)成為了自動控制領(lǐng)域的主流研究方向之一。

在AUV的路徑跟蹤控制方面,模型預(yù)測控制發(fā)揮著重要作用。文獻(xiàn)[13]考慮了有輸入約束條件下的欠驅(qū)動AUV直線路徑跟蹤問題,提出了基于MPC的AUV路徑跟蹤控制器,并比較了線性預(yù)測模型、時變線性預(yù)測模型和非線性預(yù)測模型的方案,結(jié)果表明3種方案均具有良好的跟蹤性能和魯棒性。文獻(xiàn)[14]針對含障礙物的受限工作空間,提出了一種新型非線性模型預(yù)測控制方案,引導(dǎo)AUV朝著特定方向前進(jìn),并在控制器設(shè)計(jì)中考慮了各種約束條件(如:障礙物位置、工作空間邊界、推進(jìn)器飽和速度限制等)。Shen等[15]針對AUV軌跡跟蹤問題提出了基于李雅普諾夫穩(wěn)定性的模型預(yù)測控制(LMPC)框架,在LMPC框架中考慮了驅(qū)動器飽和、推力分配等實(shí)際性的約束問題。Gao等[16]針對全驅(qū)動水下航行器的視角約束、執(zhí)行器約束和模型不確定性,提出了一種基于滑動模態(tài)觀測器的模型預(yù)測控制策略。劉昌鑫等[17]針對欠驅(qū)動AUV的約束路徑跟蹤問題,設(shè)計(jì)了一種MPC路徑跟蹤控制器,采用REMUS AUV的模型參數(shù)對提出的控制律進(jìn)行了仿真研究,實(shí)驗(yàn)結(jié)果表明控制器在顯式處理約束的同時,表現(xiàn)出良好的跟蹤效果。在文獻(xiàn)[15]的基礎(chǔ)上,Shen等[18]研究了AUV的路徑跟蹤問題,將路徑跟蹤作為首要任務(wù)優(yōu)先完成,提出了一種新的多目標(biāo)模型預(yù)測控制框架。

MPC控制策略能處理多輸入多輸出并帶約束的復(fù)雜系統(tǒng),且具有較強(qiáng)的可靠性和魯棒性。MPC優(yōu)異的控制效果依賴于精確的模型,但是AUV模型具有多自由度、非線性、強(qiáng)耦合性的特點(diǎn),而且AUV運(yùn)動數(shù)學(xué)模型中的部分水動力附加質(zhì)量、慣性矩和阻尼系數(shù)是難以精確建模的。另外,AUV在航行過程中,經(jīng)常會受到外界(如:未知深層流和表面流)的干擾,上述特點(diǎn)使得AUV路徑跟蹤控制增添了許多不確定性。

徑向基(RBF)神經(jīng)網(wǎng)絡(luò)能快速逼近系統(tǒng)動力學(xué)模型,結(jié)構(gòu)更簡單,與其他神經(jīng)網(wǎng)絡(luò)算法相比,RBF神經(jīng)網(wǎng)絡(luò)在解決實(shí)時函數(shù)逼近問題上有一定的優(yōu)勢。因此,本文針對AUV的模型不確定性引入RBF神經(jīng)網(wǎng)絡(luò)算法,通過提升預(yù)測模型的精度進(jìn)而優(yōu)化路徑跟蹤控制效果。

1 欠驅(qū)動AUV數(shù)學(xué)模型

針對AUV的路徑跟蹤控制問題,首要工作是建立AUV的數(shù)學(xué)模型。本文研究水平面上的欠驅(qū)動AUV路徑跟蹤控制問題,為了方便后續(xù)的研究分析,忽略欠驅(qū)動AUV水平面運(yùn)動和垂直面運(yùn)動帶來的耦合效應(yīng),忽略動力學(xué)模型中的非線性二次阻尼項(xiàng),建立欠驅(qū)動AUV的水平面三自由度運(yùn)動方程。

通常使用2個坐標(biāo)系來描述AUV的運(yùn)動(如圖1所示):地面坐標(biāo)系和運(yùn)載體坐標(biāo)系。地面坐標(biāo)系的原點(diǎn)O固定在地球上一處,規(guī)定OX向北為正,OY向東為正。運(yùn)載體坐標(biāo)系的原點(diǎn)OB選擇在AUV的浮心,規(guī)定OBXB沿著AUV的縱軸并指向艏向,OBYB與之垂直,向右為正。

圖1 AUV水平面坐標(biāo)系

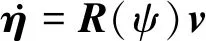
(1)

(2)

式中:M為含附加質(zhì)量的慣性矩陣;C(v)為哥氏力和向心力矩陣;D(v)為阻尼矩陣;τ是在3個自由度上的輸入力、推進(jìn)器產(chǎn)生的推力以及操縱面產(chǎn)生的操縱力。

在(1)～(2)式中,AUV的質(zhì)量、水動力附加質(zhì)量、慣性矩和阻尼系數(shù)等通常隨工作條件(包括任務(wù)和環(huán)境)的變化而變化,在實(shí)踐中難以確定。此外,海洋環(huán)境擾動往往是不可預(yù)測的、多變的。因此,AUV的運(yùn)動數(shù)學(xué)模型受到諸多不確定因素的影響。

假設(shè)AUV的縱剖面、橫剖面分別對稱,有

(3)

(4)

(5)

(6)

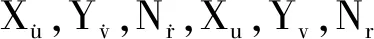
由此可得,欠驅(qū)動AUV在水平面上的運(yùn)動學(xué)方程和動力學(xué)方程,分別表示為

(7)

和

(8)

式中:m11=M11,m22=M22,m33=M33,d11=D11,d22=D22,d33=D33。

2 RBF-MPC路徑跟蹤控制器設(shè)計(jì)

令向量x表示AUV的狀態(tài),u表示控制輸入,則AUV的狀態(tài)更新方程描述為

xk+1=f(xk,uk)

(9)

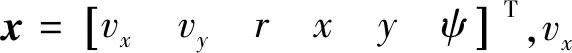
由于AUV模型中參數(shù)的不確定性,令Δf(xk,uk)表示AUV模型中的不確定項(xiàng),fnom(xk,uk)表示名義模型,則真實(shí)系統(tǒng)ftrue(xk,uk)表示為

xk+1=fnom(xk,uk)+Δf(xk,uk)=ftrue(xk,uk)

(10)

因此可以將AUV路徑跟蹤控制問題描述為以下帶約束的動態(tài)優(yōu)化問題

(11)

滿足

xk+1=fnom(xk,uk)+Δf(xk,uk)

(12)

e(k+1)=xk+1-xref

(13)

umin≤uk≤umax,k=1,…,Nc

(14)

x0=xk

(15)

式中:R和Q分別為路徑跟蹤狀態(tài)偏差的權(quán)重矩陣和控制輸入權(quán)重矩陣,(12)式表示不斷更新的AUV模型;(13)式中xk+1表示補(bǔ)償后模型的6個狀態(tài);xref是參考狀態(tài);u為控制輸入力X和力矩N;(15)式中模型預(yù)測的初始狀態(tài)x0為真實(shí)系統(tǒng)的當(dāng)前狀態(tài)xk反饋。

MPC控制器在AUV進(jìn)行路徑跟蹤時通過傳感器獲得當(dāng)前時刻的AUV狀態(tài)值;然后根據(jù)預(yù)測模型對AUV在預(yù)測時域內(nèi)的狀態(tài)值進(jìn)行預(yù)測,通過構(gòu)建目標(biāo)函數(shù)(11)式并結(jié)合約束條件(12)式和(14)式優(yōu)化求解預(yù)測時域內(nèi)的控制序列;最后選取求解得到控制序列的第一個元素作為系統(tǒng)的控制輸入。這一時刻結(jié)束后在下一個采樣時刻重新獲取AUV的狀態(tài),繼續(xù)下一周期的滾動優(yōu)化。

在實(shí)際航行過程中,AUV的結(jié)構(gòu)參數(shù)經(jīng)常發(fā)生變化。除此之外,由于水下航行器系統(tǒng)的強(qiáng)非線性和強(qiáng)耦合性,也導(dǎo)致AUV實(shí)際上難以建立精確的實(shí)際系統(tǒng)模型,影響了其跟蹤的預(yù)設(shè)路徑的精度。因此,針對模型不確定項(xiàng)Δf(xk,uk),采用RBF神經(jīng)網(wǎng)絡(luò)來進(jìn)行逼近。

RBF網(wǎng)絡(luò)結(jié)構(gòu)如圖2所示,該結(jié)構(gòu)包括3個不同的層,其中n是輸入層節(jié)點(diǎn)的個數(shù),m是隱藏層節(jié)點(diǎn)的個數(shù),l是輸出層節(jié)點(diǎn)的個數(shù)。

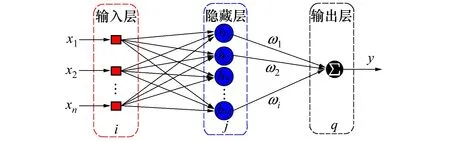
圖2 RBF網(wǎng)絡(luò)原理圖

該結(jié)構(gòu)中第一層是輸入層,輸入層X=[xi]T,其目的是將n個輸入分配給第二層隱藏層的m個節(jié)點(diǎn),隱藏層輸出H=[hj]T,其中x和hj分別是系統(tǒng)輸入和隱藏層的第j個輸出,本文選擇高斯函數(shù)作為激活函數(shù),即

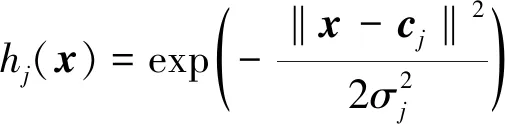
(16)

式中,‖x-cj‖表示x和cj之間的歐幾里得距離,RBF神經(jīng)網(wǎng)絡(luò)采用中心cj和寬度σj為參數(shù)的高斯基函數(shù)。

RBF第三層輸出層為網(wǎng)絡(luò)的輸出,通過線性組合隱藏層來計(jì)算網(wǎng)絡(luò)的預(yù)測輸出,從而有計(jì)算方式

(17)

式中,wjq是第j個隱藏層節(jié)點(diǎn)到第q個輸出層節(jié)點(diǎn)的權(quán)重,采用梯度下降法辨識wjq。

結(jié)合(17)式,AUV模型不確定性可表示為

Δf(xk,uk)=WTH(xk)+ε

(18)

式中:W是隱藏層到輸出層的權(quán)重矩陣;H是由(16)式計(jì)算得到的向量;ε是偏差項(xiàng)。權(quán)重矩陣W和H分別為m×l和m×1的矩陣,m和l分別表示輸入層、隱藏層和輸出層的節(jié)點(diǎn)數(shù)量。

3 仿真實(shí)驗(yàn)與結(jié)果分析

圖3 RBF-MPC結(jié)構(gòu)圖

表1 模型參數(shù)表

3.1 波形曲線跟蹤結(jié)果分析

為驗(yàn)證基于RBF-MPC的路徑跟蹤控制方法的有效性,先將參考路徑選擇為波形圖進(jìn)行測試,波形表達(dá)式選擇為

yl=6sin(0.05xl)

(19)

式中:xl為目標(biāo)橫坐標(biāo);yl為目標(biāo)縱坐標(biāo)。

AUV的初始位置為(0 m,0 m),初始航向角為0 rad,控制器的采樣間隔為T=0.1,預(yù)測步長為N=50,仿真時間為150 s。跟蹤波形的仿真結(jié)果如圖4～6所示。

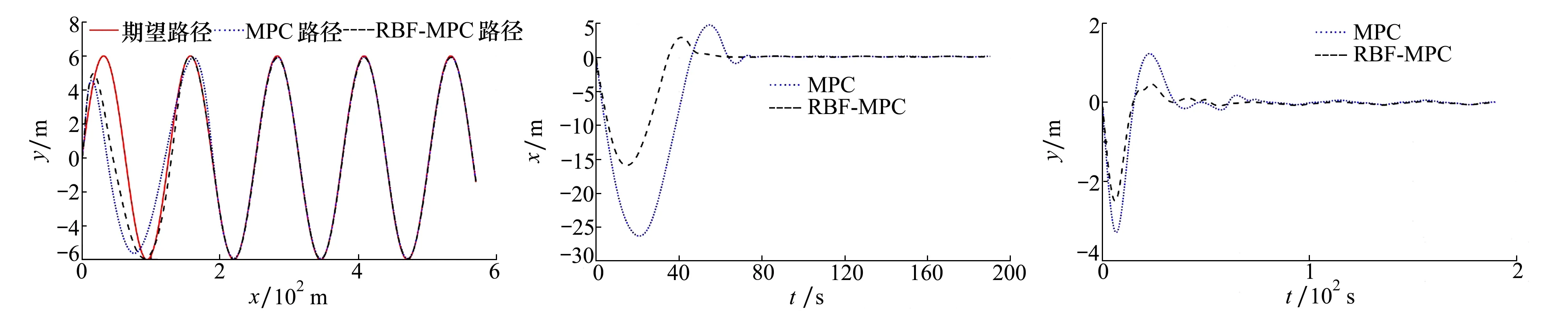
圖4 波形跟蹤控制結(jié)果 圖5 x方向跟蹤誤差對比 圖6 y方向跟蹤誤差對比

從圖4可以明顯看出,采用RBF神經(jīng)網(wǎng)絡(luò)的MPC控制器明顯誤差更小一些,在橫向100 m以內(nèi)即可跟蹤上波形,不僅收斂速度更快,而且橫縱位置的偏差更小;而MPC控制器在橫坐標(biāo)大約為180 m處才能在一定誤差內(nèi)跟蹤上波形。

為進(jìn)一步清晰看出MPC控制器和RBF-MPC控制器的跟蹤效果差異,將橫縱向位置的跟蹤偏差結(jié)果展示在圖5～6。MPC控制器在x方向達(dá)到穩(wěn)態(tài)的時間大致為72 s,位置偏差最高可達(dá)26.0 m;而RBF-MPC控制器x方向達(dá)到穩(wěn)態(tài)時間縮短為大約50 s, 位置偏差減少到13.0 m,位置誤差減少大約50%。 因此,在控制器參數(shù)、AUV模型和初始狀態(tài)等其他條件均相同的情況下,RBF-MPC控制器收斂速度更快,超調(diào)量更小。

圖7～8展示了使用MPC控制器和RBF-MPC控制器跟蹤正弦波時,控制輸入力和力矩的變化。

圖7 控制輸入力的變化曲線

圖8 控制輸入力矩的變化曲線

從變化趨勢上來看,RBF-MPC控制器產(chǎn)生的輸入波動更小,特別在30,59,70 s峰值處差異較為明顯,且在穩(wěn)態(tài)階段,RBF-MPC控制器得到的控制輸入比較平穩(wěn)。

采用2種控制器跟蹤正弦波形,驗(yàn)證了本文提出的RBF-MPC控制器的可行性。該控制器能夠有效減小模型不確定性帶來的擾動,減小系統(tǒng)的超調(diào)和穩(wěn)態(tài)誤差。

3.2 參考路徑仿真結(jié)果分析

設(shè)置AUV初始位置為(10 m,-10 m),依次到達(dá)目標(biāo)點(diǎn)位置為(17 m,-56 m),(187 m,-146 m),(208 m,-234 m),(334 m,-414 m),(488 m,-488 m),(980 m,-980 m),初始航向角0,控制器的采樣間隔T=0.1,預(yù)測步長N=50,仿真時間為360 s。

由圖9可以看出,2種控制器都能較好地完成跟蹤任務(wù),從局部放大圖可以看出,2種控制器都能產(chǎn)生平滑的運(yùn)動軌跡,但是在轉(zhuǎn)向點(diǎn)處,二者的差異非常明顯。不論是在橫坐標(biāo)為30～80 m的第一次拐角路徑跟蹤段,還是在橫坐標(biāo)為350～400 m的第二次拐角處路徑跟蹤段, RBF-MPC控制器都比MPC控制器具有更小的超調(diào)量,能更快速地減少與期望的參考路徑之間誤差,具有更好的跟蹤性能。

圖9 路徑跟蹤控制結(jié)果 圖10 x方向跟蹤誤差對比圖11 y方向跟蹤誤差對比

為進(jìn)一步清晰看出MPC控制器和RBF-MPC控制器的跟蹤效果差異,將橫縱向位置的跟蹤偏差結(jié)果展示在圖10～11。

MPC控制器在x方向的位置偏差最高可達(dá)15.5 m,而RBF-MPC控制器可以將誤差減少到6.9 m,誤差減少將近50%,在y方向的位置誤差上RBF-MPC控制器的優(yōu)勢也很顯著,特別是在第18 s到第75 s之間。因此,可以看出模型不確定性使MPC控制器存在較大的穩(wěn)態(tài)誤差,加入神經(jīng)網(wǎng)絡(luò)補(bǔ)償后,超調(diào)量明顯減少,更快達(dá)到穩(wěn)定狀態(tài)。

圖12～13展示了使用MPC控制器和RBF-MPC控制器時,控制輸入力和力矩的變化。從變化趨勢上來看,RBF-MPC控制器產(chǎn)生的輸入波動更小,特別在10,59,66 s峰值處差異較為明顯,且在穩(wěn)態(tài)階段,RBF-MPC控制器得到的控制輸入比較平穩(wěn),所耗能量更少,更利于AUV長時間水下作業(yè)。

圖12 控制輸入力的變化曲線

圖13 控制輸入力矩的變化曲線

綜上所述,在存在模型不確定和擾動的情況下,RBF-MPC在控制效果方面具有更小的路徑跟蹤超調(diào)量和更小的穩(wěn)態(tài)誤差;在控制輸入方面,具有更小輸入幅值,更加節(jié)能。與傳統(tǒng)的MPC控制器相比,綜合優(yōu)勢明顯。

4 結(jié) 論

本文中,針對AUV的路徑跟蹤控制問題,提出了基于RBF神經(jīng)網(wǎng)絡(luò)的模型預(yù)測控制器,使用RBF神經(jīng)網(wǎng)絡(luò)補(bǔ)償AUV模型不確定性。仿真結(jié)果表明,在模型存在建模誤差和顯著不確定性的情況下,RBF-MPC控制器可以將跟蹤誤差減少到6.9 m,誤差減少將近50%;加入神經(jīng)網(wǎng)絡(luò)補(bǔ)償后,超調(diào)量明顯減少,更快達(dá)到穩(wěn)定狀態(tài)。而且RBF-MPC控制器得到的控制輸入比較平穩(wěn),所耗能量更少。綜合比較, RBF-MPC控制器具有更好的跟蹤性能。