配電網通用故障定位方法研究

陳佳佳， 楊 雨， 楊 超

（1. 國網浙江省電力公司文成縣供電公司，浙江文成 325300；2. 國王瑞安市供電公司，浙江瑞安 325200；3. 三峽大學，湖北宜昌 443000）

0 引言

準確定位配電系統中的故障在系統恢復和提高可靠性方面起著重要作用[1-3]。過去，人們為開發各種類型的故障定位方法付出了巨大的努力。GOHOKAR V N 等[4]通過比較不同區段的饋線電流來確定故障位置，其中可用的數據可以從各種自動化設備中獲取。SENGER E 等[5]討論了利用本地測量和網絡數據來確定故障位置。文獻[6]通過計算視在阻抗得出故障位置，而負載由設備阻抗表示。KRISHNATHEVAR R等[7]提出了一種基于本地測量的方法。該方法假定提供了故障類型，適用于徑向配電系統。雖然存在多種故障定位方法，但這些技術一般不適用于配電系統，因為配電系統通常是不平衡的，而且配備的記錄設備非常少，通常位于主變電站。

本研究提出一種通用的故障定位方法。該方法適用于徑向系統或有不平衡的多源系統，并考慮了饋線并聯電容。這種方法避免了對故障類型信息的要求，為任何類型的故障提供了解決方案，從而消除了可能由于故障類型識別錯誤而造成的誤差。

圖1描述了一個典型的配電系統。系統包括不平衡負載、遠程電源、主饋線和側線，可以是高架或地下電纜。現有的故障定位方法需要首先確定故障類型，或者假設故障類型已知，然后推導出每種故障類型的公式。錯誤的故障類型識別將導致錯誤的故障位置計算。因此，本研究提出一種不需要識別故障類型的通用方法，從而消除因故障類型識別錯誤而產生的錯誤。

圖1 配電系統樣圖

1 方法原理

1.1 故障定位方法的基本思路

本研究提出的方法核心基于母線阻抗矩陣。在故障期間，任何總線上的電壓和電流量都可以用故障網絡的總線阻抗矩陣來表示，它是故障位置的函數。當地變電站的給定測量值以及故障點的電壓和電流都可以用故障位置來表示。故障電阻只消耗有功功率，消耗的無功功率為零，因此可以得到故障點。

為了應對內在的不平衡，配電系統在三相域中表示，并利用相域短路分析技術得出故障位置。因此，本研究提出的方法適應系統中的任何不平衡，并適用于非放射狀網絡。

1.2 轉移和驅動點阻抗的推導

圖2所示為假定三相饋線的一段配電系統單線圖，其中配電系統的剩余部分未畫出。對圖中做如下注釋：

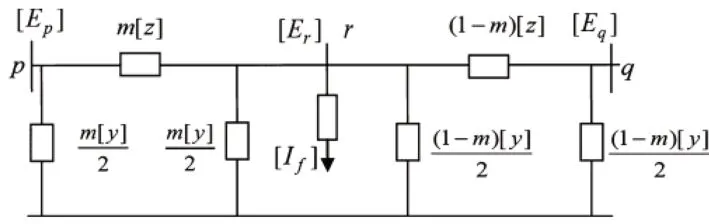
圖2 配電系統部分單線圖

n:整個配電系統的節點總數，不包括故障節點r1、r2和r3，其中一個節點對應一個單相；

p,q:母線：母線p包括節點p1,p2和p3,母線q包括節點q1,q2,和q3；

r:故障總線，包含節點r1,r2,和r3；

[Ek]:節點電壓矢量，[Ek]=[Ek1,Ek2,Ek3]T,k=p,q,r；

[If]:通過故障電阻的故障電流，[If]=[If1,If2,If3]T。If1,If2,If3分別為1，2，3相的故障電流；

[z]:饋線的總串聯阻抗矩陣，其大小為3×3；

[y]:由并聯電容得出的饋線總并聯導納矩陣，大小為3×3；

m:從母線p到故障點的單位故障距離；

[Z0]:相域內故障前的整個配電系統母線阻抗矩陣，不包括虛擬節點r1,r2和r3，其大小為n×n；

[Z]:整個配電系統（包括虛構的故障節點）的相域母線阻抗矩陣，其大小為(n+3)×(n+3)；

Zkl：矩陣[Z]中第k行第l列的元素。

在具體使用中，故障節點的編號為：r1=n+1，r2=n+2，r3=n+3。

將矩陣[Z0]展開，可以發現矩陣[Z]的前n行和n列與[Z0]相同，且其余行和列是由與故障節點相關的轉移和驅動點阻抗組成。轉移和驅動點阻抗獲得方式如下：

其中[Zkr]是節點k和故障節點之間的轉移阻抗；[Zrri]是與故障節點相關的驅動點和轉移阻抗；[u]是一個3×3單位矩陣，其第i列由[ui]表示。

上述方程對于單相、兩相或三相饋線均成立。適用時，關鍵是轉移點和驅動點阻抗表示為故障位置的函數。

1.3 故障定位推導

在檢查發生在三相饋電線上的故障時同樣不假設故障類型。根據疊加理論和轉移阻抗的含義，故障引起的電壓變化或任意母線k處的疊加電壓可寫為：

其中：

[ΔEk]為母線k處的疊加電壓，即故障期間電壓與故障前電壓的差值。總線k假設由節點k1、k2和k3組成。在實際中，只有存在的節點才會出現在方程中。

由式（4）可得：

故障期間故障節點處的電壓由下式給出：

其中：

[Er]和[Er0]分別是故障期間和故障前故障節點處的電壓。

故障前電壓可根據故障位置和母線p、q故障前的節點電壓表示：

其中，[Ep0]和[Eq0]是相應節點處的故障前電壓矢量，可以利用變電站故障前電壓和電流以及饋線的負載阻抗來估計，或者直接從測量設備獲得。

根據式(8)，故障電阻消耗的復功率計算如下：

其中“*”表示復共軛。故障電阻只消耗實數功率，所以S的虛數部分為零。

從式（1）～（4）、（9）和（13）可以看出，存在一個未知變量m。m可通過牛頓-拉夫遜方法確定。這清楚地表明，本研究提出的方法不需要故障類型信息，并且不規定相間故障電阻相等，即它自動考慮了相間不相等的故障電阻。

為了減輕負載變化的影響，使用了負載補償技術[10]。其基本思想是根據變電站測得的故障前電壓和電流計算負載水平，然后相應地縮放靜態負載阻抗。在本文第3章中說明了該方法的有效性。

2 實驗評估

采用Matlab Sim Power Systems（電路仿真模塊）生成不同類型、位置和故障電阻的故障瞬態波形。然后利用快速傅里葉變換（FFT）計算所需的電壓和電流相量，并將其輸入到故障定位算法中以獲得故障位置。饋線的并聯電容采用標稱π模型。圖3所示的配電系統將用于該方法的可行性評估[11]。

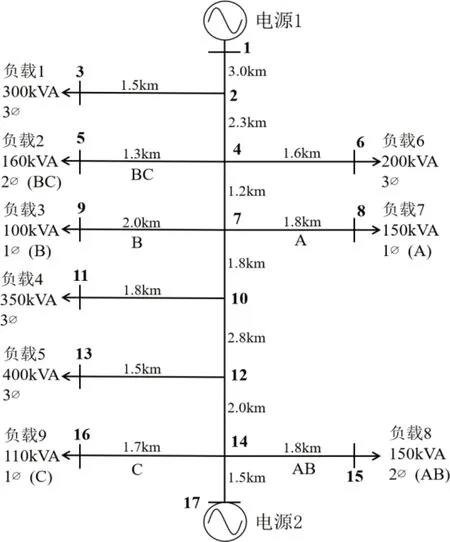
圖3 配電系統實例

該系統包括三相、兩相和單相側及負載。例如，負載7 為A 相負載，由主饋線單相側抽頭供電。饋線長度以km 為單位，負載等級和相位已標注。假設9 個負載的功率因數均為0.9, 饋線串聯阻抗和并聯導納數據參見文獻[12]。

在實驗中，采用0.5 p.u.的初始值進行故障定位，所有情況均可在10次迭代內收斂。用百分比誤差來衡量估計的精確度，算法如下：

仿真實驗包含了不同故障位置的不同故障類型，從饋線上0.1 p.u.～0.9 p.u.的各部分故障阻抗，從1 Ω～100 Ω 的接地故障阻抗和1 Ω～10 Ω 的非接地故障阻抗，本節都給出了典型結果（見表1）。

表1 定位方法得出的故障估計值

表1給出的方法能夠自動處理相間故障阻抗不相等的情況，例如在故障區間1～2 中的LLG 故障，實際相間阻抗為1.00 Ω 和2.00 Ω，接地阻抗為10.00 Ω。其中對于在故障區間14～15 上發生的LG 故障，使用短路分析來生成故障數據以測試算法，因為仿真軟件不允許零值故障電阻。結果表明，該算法可以進行較為精確的故障定位。

此外，還研究了測量誤差對故障定位估計影響的可能性。表2 所示為在饋線區間2～4 上發生故障時電流電壓測量誤差下的故障位置估計。前3列列出了實際故障類型、故障阻抗和故障位置。第4列和第5列分別顯示了電流測量誤差為1%和2%的情況下的故障位置估計。可見測量的電流誤差越大，對故障定位的誤差影響越大。電壓測量誤差帶來的影響與電流測量誤差的影響類似，在表中未列出，第6 列和第7 列表示當電流和電壓測量值同時存在誤差時的結果。仿真結果表明，該方法對電流和電壓測量誤差具有較強的魯棒性。

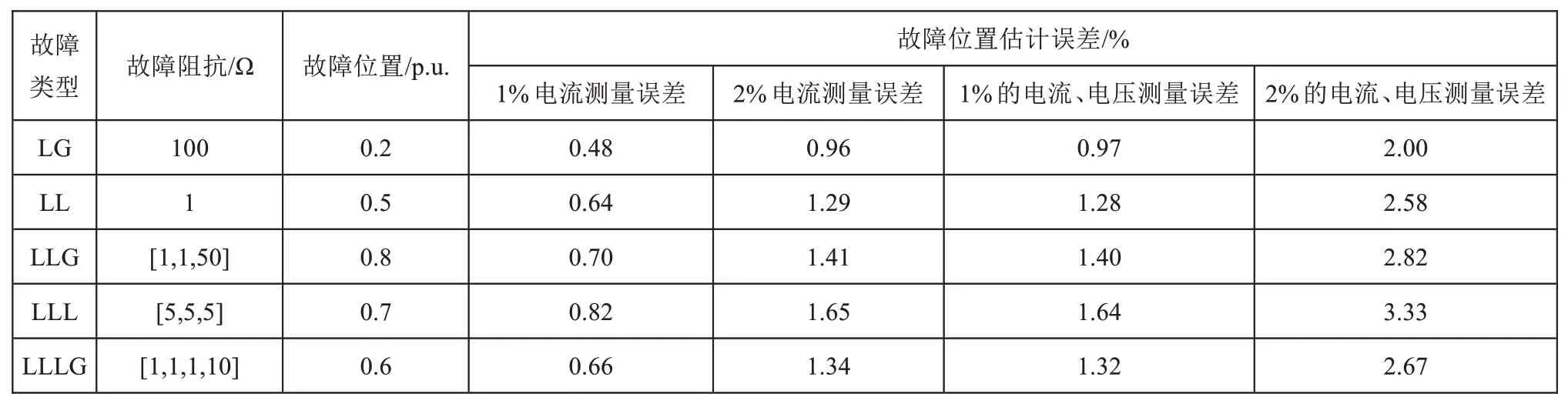
表2 測量誤差對故障定位估計的影響

該算法是利用額定條件下得到的負荷等效阻抗模型，負荷變化會導致定位誤差。表3 所示為在施加負載變化的情況下發生在饋線故障區間4～7上的故障位置估計。前3列分別列出了實際故障類型、故障阻抗和故障位置。其余3 列給出了分別對應于5%、10%和20%負載變化的故障定位誤差。結果表明，當故障阻抗增大時，由于負載變化，LG故障的定位估計受影響較大。對于LG 故障，故障阻抗增大導致故障電流變小，因此負載精度在確定故障位置時起更大作用，從而對故障定位精度具有更大影響。對于其他類型的故障定位估計對負載變化不敏感。

表3 負荷變化對故障位置估計的影響（無負荷補償）

為了減輕負載變化的影響，利用類似于文獻[10]中提出的方法來補償負載變化。利用本地變電站實測的故障前電壓和電流來調節負荷阻抗。遠程電源的功率貢獻因子假定為常數。表4 所示為4種單獨負載變化的情況。在前兩種情況下，負載分別平均減少20%和30%；在后兩種情況下，負載分別平均增加20%和30%。

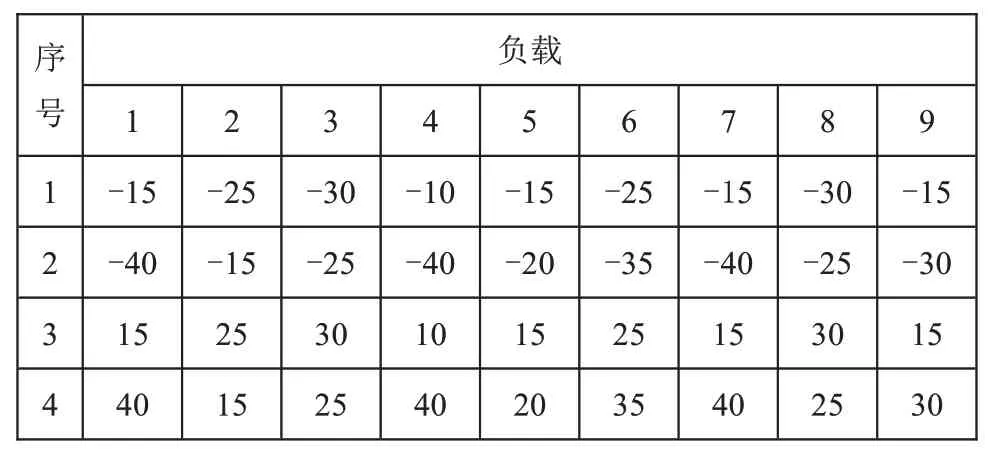
表4 單個負載變化 （單位：%）

對應于4 種負載變化情況，表5 給出了利用負載補償技術來定位發生在饋線故障區段4～7 上的故障定位估計。結果表明，采用負荷補償技術后，故障測距精度有了很大提高。

表5 采用負荷補償技術進行故障定位的有效性

本次實驗測試的是非網狀系統，所用方法對于網狀系統的適用性可能需要在今后進一步研究。此外，對于非線性負載情況和故障電流與負載電流相當的高阻抗故障情況，所提方法的性能還需要進一步研究。

3 結論

本研究提出了一種新的故障測距方法。該方法僅利用局部測量值，既適用于輻射狀配電網，也適用于非輻射狀配電網，并對不平衡并聯電容建模。該方法不需要故障類型，通過減少迭代步驟，為任何類型的故障提供了直接和通用的解決方案。 仿真研究表明，該方法具有較高的精度，受潛在的測量誤差和負載變化影響較小。

此外，雖然計算故障位置不需要知道故障類型，但故障類型可以在此之后作為一個副產物得到，可能對其他故障分析應用有用。如果由于側線的存在而出現多次估計，可能會需要根據得到故障位置后流過故障電阻的故障電流來消除偽估計。