考慮市場交易的新型電力系統調度輔助決策方法研究

吳任博,劉淑琴

(山東大學 電氣工程學院,濟南 250000)

0 引 言

隨著當今電力控制和通信能力的提高,以及多樣化的需求側技術出現,用更靈活的新型電力系統取代現有的電力系統成為可能[1]。提高系統控制準確性的一個挑戰是在電力市場出清機制中整合負荷管理計劃和主動配電網技術,以反映市場結果對新興技術的影響和依賴[2]。在目前方法中,實體電網及其組件(例如,儲能設備)的實際動態在很大程度上被忽略。這種簡化在極大系統的情況下是可接受的,以達到較優的解決方案,但對于其他情況可能會產生不可行結果[3]。事實上,每個智能電網的決策過程都是一個復雜的優化問題,既有連續決策,也有離散決策。當獨立的智能電網融入電力市場運行并與之互動時,如何解析地確定獨立智能電網的運行策略,基本上是個未知數[4]。因此,考慮到這些關鍵因素和相互作用,必然需要一種有效的能源管理方法來支持電力市場中智能電網的最優調度和運行計劃。

為了應對現代電力市場中智能電網的運行挑戰,學者開發了許多輔助決策模型和求解方法。在文獻[5]中,提出了一個的兩層模型來確定電力市場中負荷削減和靈活負荷(即需求響應組合)的最優調度。在文獻[6]中提出了Stackelberg博弈模型來研究電網運營商和配備了需求響應用戶之間的交互作用。文獻[7]建立了電力供給方和終端用戶之間的Stackelberg博弈,其中供給方充當追逐利潤的領導者,而終端用戶充當福利最大化的追隨者。文獻[8]提出了智能電網零售商作為能源市場和終端用戶之間的中介機構的能源定價和調度的雙層優化模型。文獻[9]中引入了一個隨機雙層模型,在該模型中,上層的電網運營商最小化總的運營成本,而下層的需求響應聚合體最大化利潤。上述文獻將智能電網建模為受控或價格接受者,在電力市場內由電網運營商作為綜合負荷或電源運營管理。這些假設在很大程度上是不切實際的,因為考慮如儲能、光伏等分布式能源,基本上是私有的,幾乎沒有可能讓電網運營商全權管理或運營。

在最近的一些工作中,考慮了部分電網的決策獨立性。在文獻[10]中討論了一組主動配電網和輸電系統之間的能量管理問題。文獻[11]提出了一個框架和迭代算法來協調輸電網和多個微電網,以找到這些獨立系統的最佳運行點。文獻[12]考慮了由引導者和跟隨者組成的多子網系統的分散結構,并通過雙層優化來解決能量管理問題。單個子網在最壞情況下進行多階段穩健優化以最小化運行成本,而在系統層面(即上層),通過最小化日常運行成本來進行能量管理。然而這些工作忽略了電力市場及其與多子網組成的新型電力系統的相互作用。

文獻調研顯示,與豐富的智能電網運行和優化研究文獻相比,考慮智能電網自主性和市場運行的模型研究較少。事實上,主動配電網是一個關鍵組件,它將該地區的各種可再生資源、儲能設備和響應負載互聯在一起,以滿足用戶的電力需求。因此,應該采用一種考慮所有這些因素和相互作用的分析方法來確定電網的實際運行策略。因此,文中開發了一個基于市場的框架來研究電力市場和包含多個主動配電網的新型電力系統的相互作用,并進行輔助決策。在所提出的方法中,子電網預測市場價格,并可以相應地影響市場數量。也就是說,其參與市場博弈,這種互動通過雙層優化來建模。頂層的市場運營商對日前市場進行出清,而較低層的多個獨立子電網按順序行動,以確定其最優調度。在這里,每個子電網都是一個自組織系統,其運行和管理自己的網絡,以利用該地區各種相互連接的可再生資源、儲能設備和響應能力較強的負載。在市場方面,假設運營商收集報價,并使用機組組合問題結算日前市場。使用二階圓錐交流潮流方法來求解運營商優化問題,以考慮輸電系統的電壓和無功約束。

將子電網的物理特性建模為這種類型的雙層優化產生的最大困難是下層問題決策的離散特征。這是一個巨大的計算挑戰,目前大多數可用的求解技術主要依賴于缺乏計算效率并可能導致次最優的啟發式、近似或簡化建模方法。與現有方法不同,本文擴展了文獻[13]中的重構和分解方案,以求解雙層優化問題。

1 優化建模

在這一部分中,給出了考慮獨立子電網最優運行的雙層優化方案,考慮了混合整數規劃、二次規劃和線性規劃。

1.1 模型符號

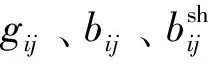
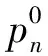
1.2 建模假設

圖1描述了所提出的雙層優化模型的結構。上層優化給出常規發電機組的啟動、關閉和調度決策,最小化系統總成本。下層優化對應著每個子電網內部能耗優化,給出負荷管理、儲能充放電等具體決策。假設發電機組向市場運營商提交報價,這些報價體現了其實際運營成本和約束[14]。文中,運營成本包括可變(運行)成本、啟動成本、關閉成本和空載成本。運行約束包括爬坡率、最小正常運行時間和停機時間以及最小和最大發電量。一旦收集到報價,就決定機組的啟動和關閉。

圖1 輔助決策模型架構

1.3 雙層優化模型

如前所述,市場運營商收到來自發電部門的報價,其中包括運營成本數據和運營限制。然后執行多階段優化,以出清日前市場。這是上層優化,其解決方案得出了常規發電機組的啟動、關閉和調度決策。將與輸電系統相連的子電網的需求視為因變量,由下層優化迭代確定。

利用二階二次交流潮流模型,上層優化問題可寫成:

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

vit-vit-1=uit-sit,uit,sit∈{0,1} ?i∈Δ,t∈T

(14)

(15)

(16)

(17)

Cijt=Cjit,Sij=-Sjj,Cijt≥0 ?ij∈Ω,t∈T

(18)

(19)

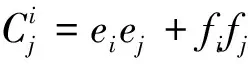
(20)

(21)

假設系統內存在一些獨立的子電網,它們通過變電站連接到輸電系統,并與主電網交換電力。

每個子電網的運營商預測市場價格(在連接節點),并通過使用混合整數線性規劃最小化其實際和無功消耗來計算最優運行決策。在子電網優化問題中,考慮了配網的技術約束以及各種需求側技術(儲能、需求響應等)。因此,對每個輸電節點i處的子電網都求解以下最優潮流問題:

(22)

?n∈Φi,t∈T

(23)

?n∈Φi,t∈T

(24)

Unt=Umt-2(rmnpmnt+xmnqmnt) ?n∈Φi,m∈Φi(n),nm∈Ni,t∈T

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

znt∈{0,1} ?n∈Φi,t∈T

(36)

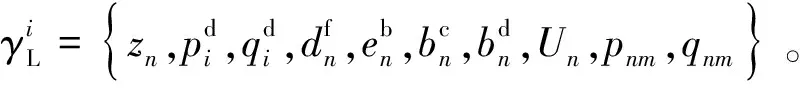
由此可見,下層優化問題本質上是一個混合整數線性規劃。各子電網運營商通過求解該模型來計算最優自耗量及其調度決策。采用KKT條件或強對偶性的傳統重述方法,以等價的對應問題取代下層優化問題,在此背景下并不適用。在下文中,提出了一種重構和分解方法來計算該問題。

2 求解方法

優化模型式(1)、式(22)由一個混合整數二階錐規劃的上層優化和多個混合整數線性規劃(Mixed Integer Linear Programming,MILP)下層優化問題組成。為了計算這個雙層問題,使用并擴展了文獻[13]中提出的重構-分解算法,該算法將原始模型劃分為一個主問題和多個子問題。

為了使本節中的論述更易理解,首先給出雙層優化問題式(1)、(22)基于矩陣的表示法,如下所示:

minax+by

(37)

s.t.

By+Cri=d

(38)

Ax+Dy≥l,x∈{0,1}

(39)

‖Hy‖≤hy

(40)

其中:

ri∈argmin{ei(ri+yi):

(41)

s.t.

Giwi+Eiri+Oiyi=fi

(42)

Fiwi+Kiri≤ki

(43)

ri≥0,wi∈{0,1}}?i∈Δ

(44)

其中x和y表示上層優化二進制和連續變量,ri和wi表示與輸電節點i處的子電網相關聯的下層優化的連續和二進制變量。使用適當維度的系數矩陣或向量(A,a,B,b,Ei,ei,l,D,d,Fi,fi,Gi,H,h,Ki,ki,Oi)使這些變量相關聯。在約束式(40)中,使用符號‖·‖表示向量(矩陣)的l2范數。方程式(41)表示目標函數,式(42)～式(44)表示與輸電節點i處的每個子電網相關聯的下層優化問題的原始約束。

為了給算法提供可分解的結構,遵循文獻[13]中通過復制上層問題中的下層變量和約束并增加一個額外的約束式(49)來重新制定雙層優化問題式(37),如下所示:

minax+by

(45)

s.t.

式(38)～式(40)

(46)

(47)

(48)

(49)

s.t.

Giwi+Eiri+Oiyi=fi,Fiwi+Kiri≤ki

(50)

ri≥0,wi∈{0,1}}?i∈Δ

(51)

(52)

s.t.

(53)

(54)

(55)

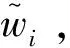
2.1 子問題

對于給定的上層決策(x*,y*),以及連接到輸電節點i∈Δ的每個子電網,計算以下子問題SP1i:

(56)

s.t.

(57)

Fiwi+Kiri≤ki:μi

(58)

ri≥0,wi∈W

(59)

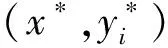
SP2:Ψ(x*,y*)=minax+by

(60)

s.t.

式(57)～式(59)

(61)

(62)

SP2是一個容易計算的MILP問題。

2.2 主問題

1)步驟1:設置LB=0、UB=∞、τ=0。

2)步驟2:求解以下主問題:

MP:Γ=minax+by

(63)

s.t.

式(38)～式(40),式(47)～式(48)

(64)

(65)

(66)

(67)

(68)

報告最優解(x*,y*)并更新LB=Γ。

5)步驟5:如果UB-LB≤,則停止求解UB。否則,τ=τ+1并返回步驟2。

該算法動態地提供上界(從子問題)和下界(從主問題),并在每次迭代中向主問題添加新的變量和約束,直到界之間的差異不大于最優性容差。

雖然主問題在每次迭代中都會隨著維度的增加而變得繁瑣,但該算法的關鍵優勢在于它可以在很少的迭代次數和算法操作中產生最優解。在案例研究中,在大多數情況下,算法在3次迭代后可得出最優解,最多只需要4次迭代。

3 仿真分析

3.1 示例系統

考慮一個六節點輸電網絡,有四臺發電機組和兩個子電網,標記為SG1和SG2,其余測試參數見文獻[15]。子電網分別連接到節點2和節點4,如圖2所示。每個子電網有一個光伏發電和一個儲能設備連接到同一節點。在24小時的時間范圍內,考慮了以下案例條件:

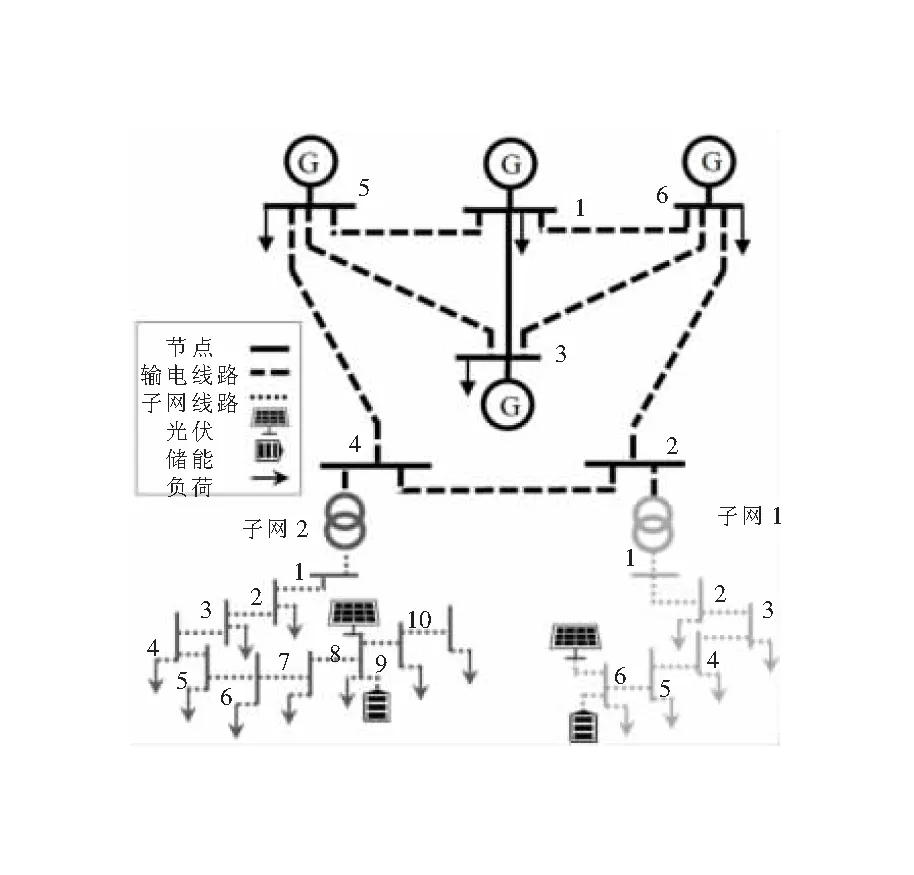
圖2 示例系統單線圖

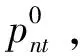
2)改變光伏-儲能的位置,并且重置條件與案例1相同;

3)假定儲能的充放電次數不受限制,其余條件與案例1相同;

4)每個節點處的可轉移需求增加到15%,其余條件與案例1相同;

5)與案例4類似,不同之處在于50%的子電網節點具有可轉移的需求,其余節點的需求是固定的。隨機選擇具有可轉移需求的節點;

6)子電網的拓撲結構發生了變化。在子電網1中,線路2、3和5上的開關斷開,線路6、7和8上的開關閉合。此外,在子電網2中,線路4、5和8上的開關斷開,線路10、11和12上的開關閉合;

7)沒有建模子電網,負荷產生條件類似于案例3。這種情況基本上代表了一個聚合的智能電網模型。

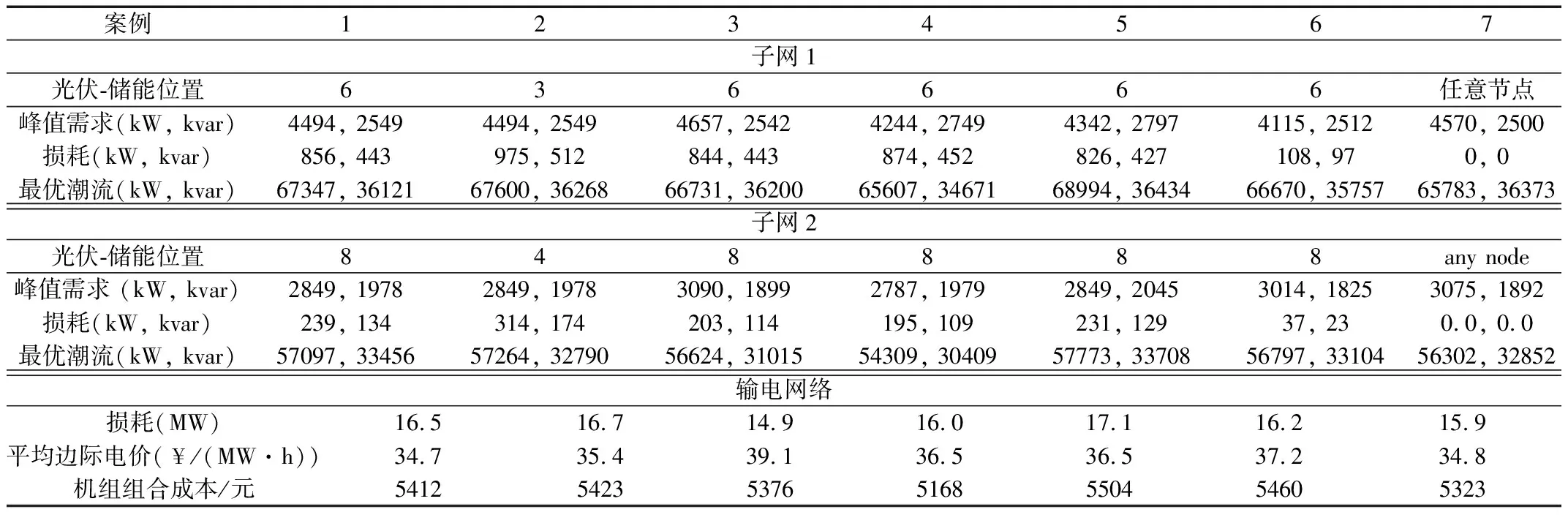
表1 優化示例系統輔助決策結果

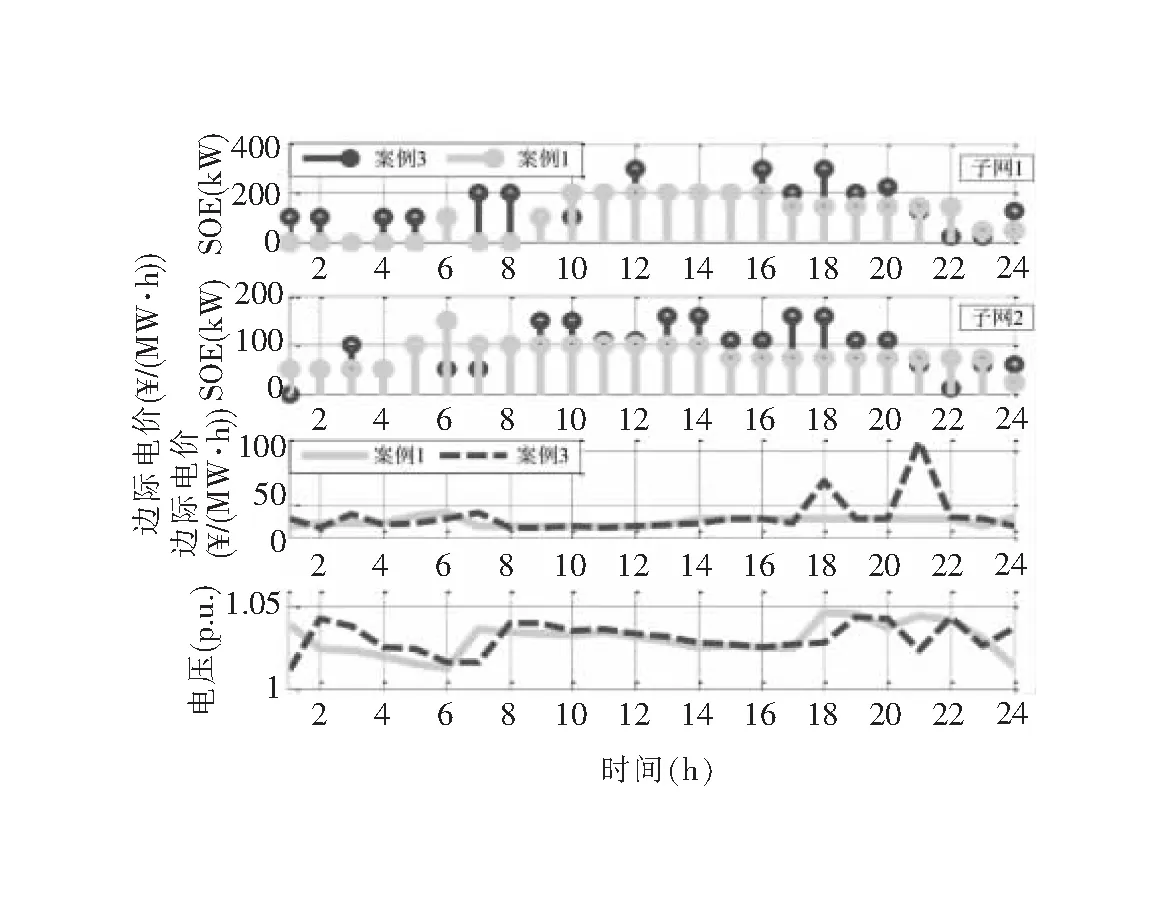
圖3 案例1和案例3的測試結果:SOE、節點邊際電價和輸電網的電壓曲線

為了探討可轉移需求對子電網和主電網的影響,對于案例1和案例4,在圖4中描繪了這些網絡的損耗和機組組合成本。在案例4中,通過將需求響應(可轉移)增加5%,在大多數時間內降低了網絡損耗和成本。圖5給出了輸入到子電網2的有功和無功功率以及案例4和5的輸電網絡的平均節點邊際電價。如前所述,在案例5中,只有50%的子電網節點具有可轉移需求,因此,在大多數時間內,子電網的功率輸入增加,這提高了輸電網絡的邊際電價。這個實驗清楚地說明了主動配電網中響應性需求的位置如何對市場結果產生顯著影響。在案例6中,假設每個子電網的運營商可以更改電網配置。在此觀察了這些行為對市場結果的影響。例如,與案例1相比,案例6的平均邊際電價增加了7%。在案例7中,不對子電網進行建模,因此使用聚合負荷生成模型。從表1可以看出,在這種情況下,輸電損耗增加,子電網的高峰需求減少。因此,與子電網建模的案例3和5相比,發電的機組組合成本卻降低了。為了更好地說明,圖6中描繪了在案例3和7中的輸電系統的平均節點邊際電價和損耗。觀察到案例3出現平均邊際電價的急劇增加和某些小時的損失,在案例7由于過于簡化而基本上消除了這些情況。

圖4 案例1和案例4的測試結果:損失和單位生產成本

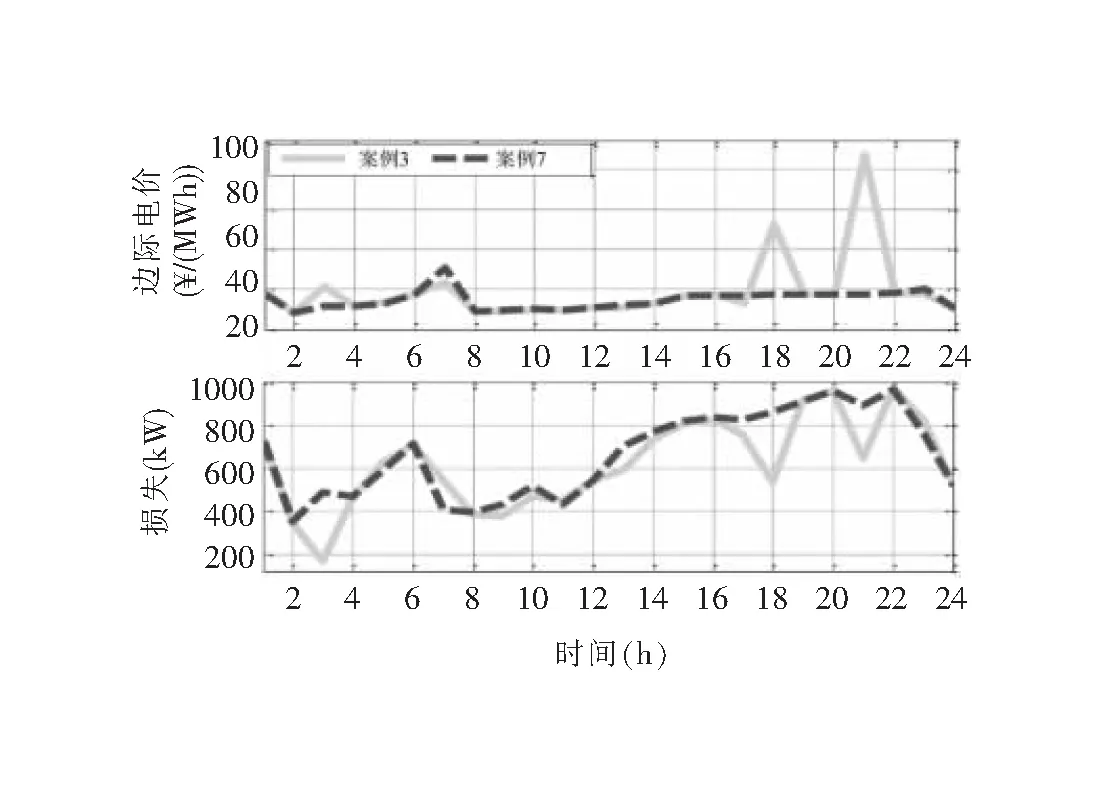
圖6 案例3和案例7的測試結果:平均邊際電價和輸電網絡損耗

最后,圖7顯示了在本節研究的情況下,發電機的每小時投入狀態(標記為Gi,i=1,...,4)和儲能設備的充電/放電模式(標記為SGi,i=1,2),白色方塊表示投入或充電狀態,黑色方塊表示退出或放電狀態。它簡單地展示了下層優化問題(即子電網)的負荷生成條件或建模細節的變化如何影響上層問題中的機組組合時間表。

圖7 系統設備的每小時開/關狀態和儲能設備的充放電運行模式

3.2 30節點系統測試

將輸電系統改為30節點系統[16]。并使用4節點、18節點、22節點和33節點四種子電網。它們分別連接到20、18、30和15輸電節點。測試參數取自文獻[15]。這些子電網分別有2、3、4、5個光伏-儲能系統。在24小時內,研究了以下案例:

1)假設10%的節點需求是可轉移的。對子電網中的所有儲能設備施加有限數量的充電/放電次數。

2)與案例1一樣,改變了原有的網絡拓撲,保留了光伏-儲能位置。與原有的網絡拓撲相比,在子電網1中,線路2和3上的開關是斷開的。在子電網2中,線路8、12、13和17上的開關斷開。在子電網3中,線路3、8、11和15上的開關斷開。在子電網4中,線路7、9、14、32和37上的開關斷開。

3)隨機改變光伏-儲能的位置,并且重置條件與案例1相同。

優化結果如表2所示。觀察到由于光伏-儲能位置或子電網配置的變化而導致市場結果和子電網調度決策的變化。例如,與案例2相比,案例1和案例3對子電網的目標更高。此外,案例2的拓撲變化降低了子電網損耗和上層問題的社會成本。因此,從表2中的輸電系統指標可以看出,輸電層面的子電網簡化聚合模型將低估市場運行成本,并得出不準確的結果。

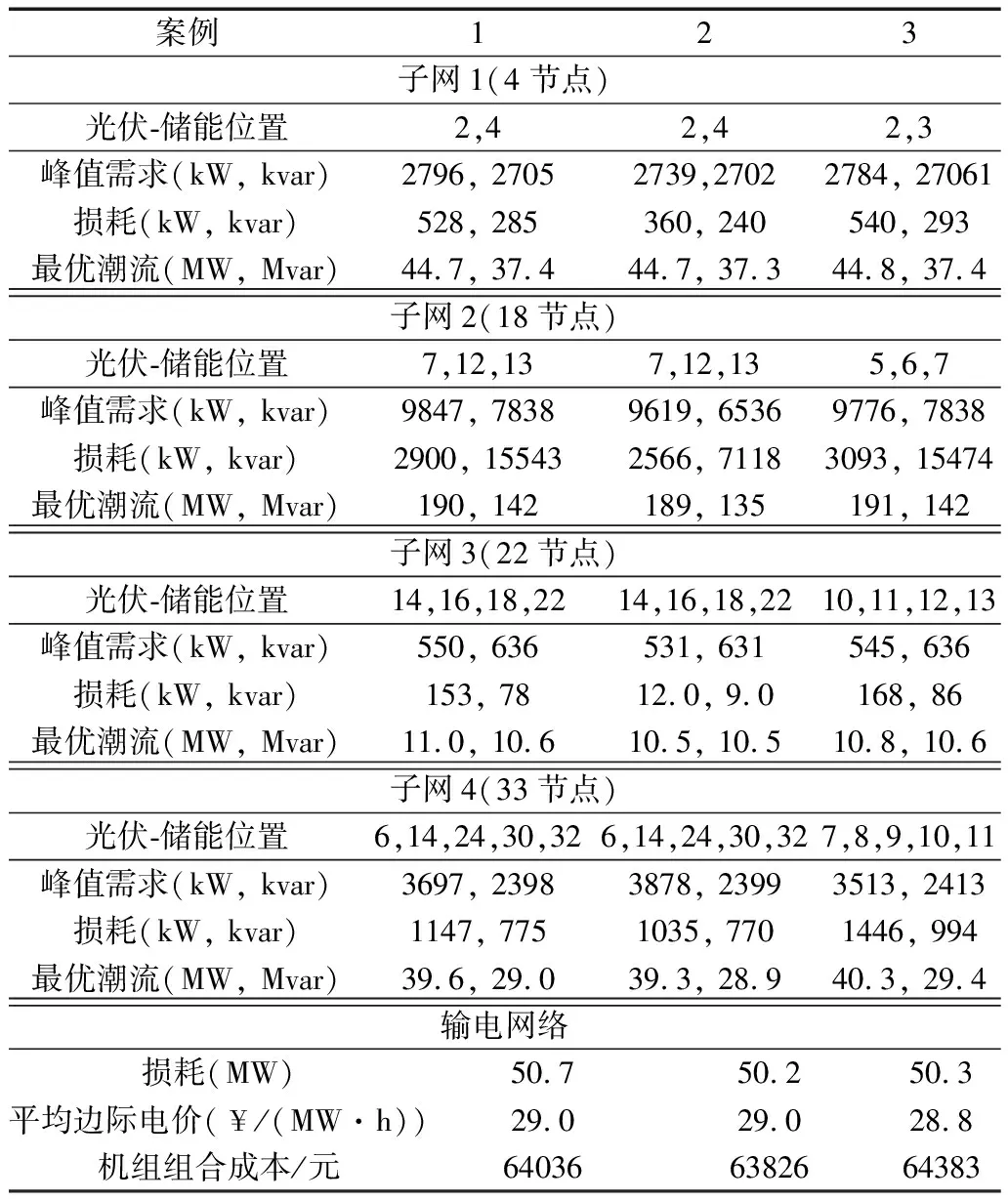
表2 優化后30節點系統輔助決策結果

3.3 57節點系統測試

將該方法應用于57節點系統[17]。該系統由7臺發電機和80條線路組成。文中假設有四個子電網連接到該系統。子電網包括節點3處的13節點系統、節點9處的18節點系統、節點52處的22節點系統以及節點42處的33節點系統。

表3給出了三種情況下的優化結果。這些情況與上述30節點系統中的情況類似。在案例1中,假設10%的節點需求是可移動的,并且儲能設備的充放電次數有限。在案例2中,光伏-儲能位置改變,其余條件與案例1相同。在案例3中,修改子電網拓撲,其余條件類似于案例1。

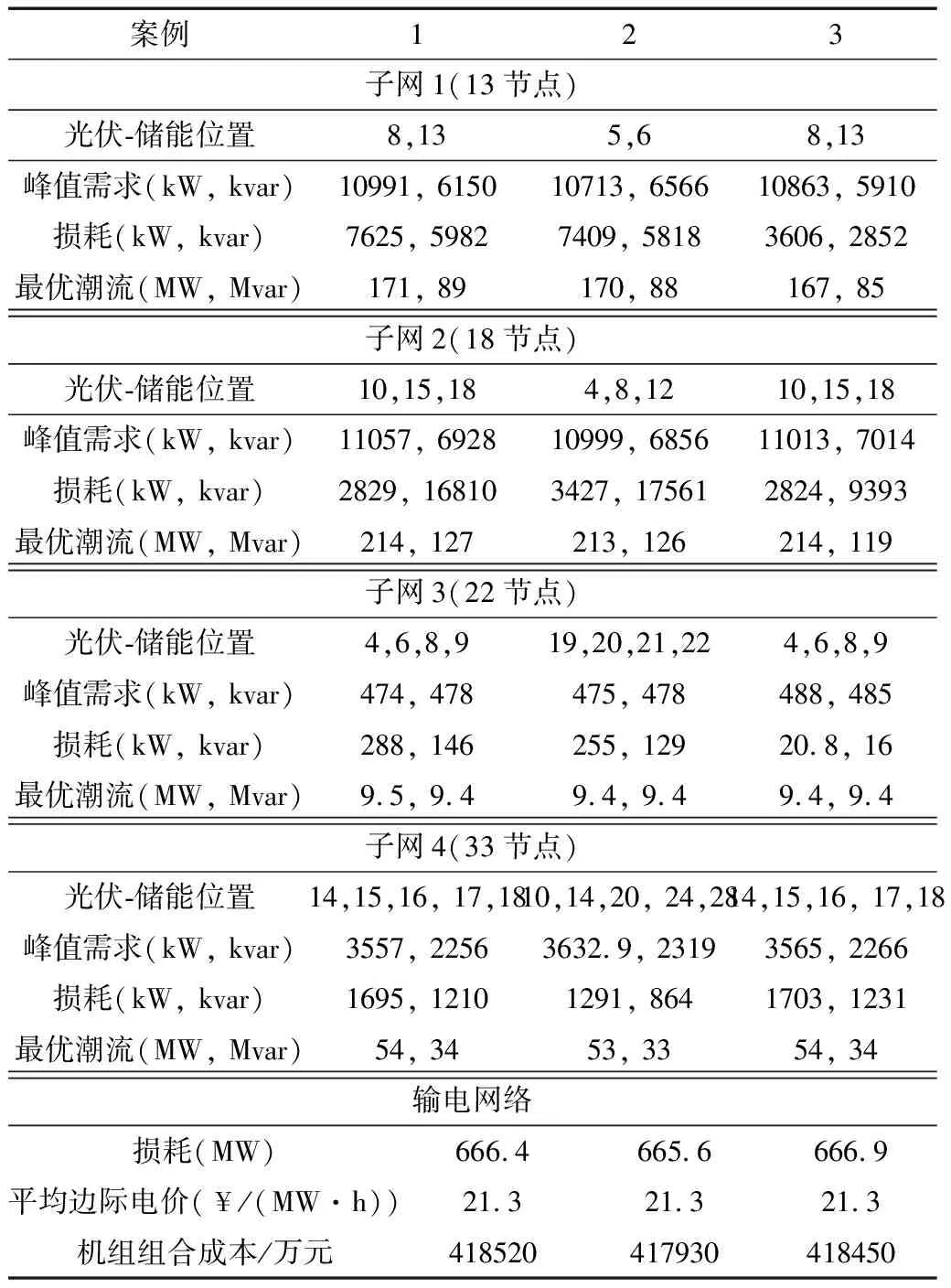
表3 優化后57節點系統輔助決策結果

從表3可以看出,子電網的最優決策的變化反映在市場結果中。例如,當子電網中的光伏-儲能位置與案例2相同時,輸電損耗和社會成本達到最低值。這表明實際市場結果取決于子電網的反應和運行決策,以及在對這些系統建模時考慮的物理細節水平。

4 結束語

本文提出了一種在日前市場運行中集成自治子電網輔助決策問題的建模框架。制定了一個雙層優化方法來分析市場運營商與包含分布式能源以及需求側技術的獨立子電網之間的相互作用。上層優化問題使用二階二次交流潮流模型來描述日前市場的出清過程。下層問題優化了自治子電網的能耗管理,其中考慮了與儲能設備和可轉移需求有關的決策的混合整數性質。考慮到上層問題和下層問題的混合整數結構,提出了一種重構分解方法,使用一個主問題和多個子問題迭代地求解優化模型。在三個測試系統上對所提出的方法進行了評估,觀察到子電網的聚合建模方法使用了配電系統的簡化模型并忽略了儲能設備的實際特性,將導致產生不準確的結果。所提出的方法通過捕獲物理輸配電系統、下層決策過程的離散性以及電力市場和子電網之間的相互作用來提高求解精度。

未來研究的可能方向包括納入需求側技術的更多特征,如需求響應的反應時間、電動汽車等,并評估它們對市場運行的影響。